LoginSignup
11
4
@ht_deko(Hideaki Tominaga)

Delphi で基本的な図形を描画する

Last updated at Posted at 2020-05-05

はじめに

Pascal の書籍にある 図形を描画するアルゴリズム を試したい事があります。

標準 Pascal には図形描画のライブラリが用意されていないため、書籍では独自の描画ルーチンがある事にして話が進みます。つまり、図形描画アルゴリズムを試すには、各 Pascal 処理系で描画ルーチンを自前実装する必要があります。

『アルゴリズム + データ構造 = プログラム』の描画ルーチン

setPlot() と Plot() が用意されているという事になっています。

ルーチン 意味
setPlot() グローバル変数 x および y の値をペンの位置とする
Plot() ペンの位置からグローバル変数 x および y が示す座標まで線を引く

『アルゴリズムとデータ構造』の描画ルーチン

ユーティリティモジュール LineDrawing が用意されているという事になっています。

ルーチン 意味
line(k, u) 45 k 度の方向へ、単位線分 u だけ線を引く。

k は 0 (0°) ～ 7 (315°) です (8 方向)。単位線分が 1 かつ not Odd(k) の場合、長さ 1 の線が引かれます。単位線分が 1 かつ Odd(k) の場合、長さ √2 の線が引かれます (つまりは対角線)。

『コンピュータアルゴリズム辞典』の描画ルーチン

Dot() が用意されているという事になっています。

ルーチン 意味
Dot(x, y) (x,y) の位置に点を描画する
Line(x1, y1, x2, y2) (x1,y1) から (x2,y2) へ線分を描画する
Circle(Xcenter, Ycenter, Radius) (Xcenter, Ycenter) を中心座標とした半径 Radius の円を描画する

Delphi で図形を描画する

今回は『コンピュータアルゴリズム辞典』の図形描画アルゴリズムを簡単に試せるユニットを作ってみる事にしました。

図形描画ユニット uCAGRAPH

まずはこのユニットをファイルとしてどこかに保存しておいてください。

uCAGRAPH.pas
unit uCAGRAPH;

{$DEFINE HASVCL}
{$IFDEF CONDITIONALEXPRESSIONS}
  {$IF CompilerVersion >= 25.0}   // XE4
    {$LEGACYIFEND ON}
  {$IFEND}
  {$IF CompilerVersion >= 23.0}   // XE2
    {$DEFINE HASFMX}
    {$IF CompilerVersion >= 26.0} // XE5
      {$DEFINE NEWFMX}
    {$IFEND}
    {$IF CompilerVersion >= 27.0} // XE6
      {$DEFINE NEWENUM}
    {$IFEND}
    {$IFNDEF MSWINDOWS}
      {$UNDEF HASVCL}
    {$ENDIF}
  {$IFEND}
{$ELSE}
  {$DEFINE OLDDELPHI}
{$ENDIF}

(*
  {$DEFINE UseOriginalDrawAlgorithm}
*)

interface

uses
{$IFDEF HASFMX}
  {$IFDEF HASVCL}
  { VCL }
  Vcl.Graphics, Vcl.Forms, Vcl.Controls, Vcl.ExtCtrls,
  {$ENDIF}
  { FMX }
  {$IFDEF NEWFMX}FMX.Graphics, {$ENDIF}FMX.Forms, FMX.Controls, FMX.Types, FMX.Objects,
  { COMMON }
  System.Types, System.SysUtils, System.UITypes;
{$ELSE}
  { VCL }
  Graphics, Forms, Controls, ExtCtrls,
  { COMMON }
  {$IFDEF OLDDELPHI}Classes, {$ELSE}Types, {$ENDIF}SysUtils;
{$ENDIF}

  (***** グラフィックの初期化 *****)
{$IFDEF HASVCL}
  procedure InitGraph(var PaintBox: {$IFDEF HASFMX}Vcl.ExtCtrls.{$ENDIF}TPaintBox); {$IFDEF HASFMX}overload;{$ENDIF}
{$ENDIF}
{$IFDEF HASFMX}
  procedure InitGraph(var PaintBox: FMX.Objects.TPaintBox); overload;
{$ENDIF}
  procedure SetFlipMode(Flip: Boolean);

  (***** 描画ルーチン *****)
  procedure Dot(X, Y: Integer);
  procedure Line(X1, Y1, X2, Y2: Integer);
  procedure Circle(Xcenter, Ycenter, Radius: Integer);

  (***** プロッタのシミュレーション *****)
  procedure InitPlot;
  procedure MoveAbsolute(X, Y: Real);
  procedure DrawAbsolute(X, Y: Real);
  procedure MoveRelative(X, Y: Real);
  procedure DrawRelative(X, Y: Real);
  procedure DrawCircle(R: Real);

implementation

type
  TFrameworkType = (fwVCL, fwFMX);

var
  LastX, LastY: Real;
  CMaxY: Integer;
  UseFlip: Boolean;
  FrameworkType: TFrameworkType;
{$IFDEF HASFMX}
  {$IFDEF HASVCL}
  CanvasVCL: Vcl.Graphics.TCanvas;
  {$ENDIF}
  {$IFDEF NEWFMX}
  CanvasFMX: FMX.Graphics.TCanvas;
  {$ELSE}
  CanvasFMX: FMX.Types.TCanvas;
  {$ENDIF}
{$ELSE}
  CanvasVCL: TCanvas;
{$ENDIF}

(***** グラフィックの初期化 *****)

procedure InitParam;
begin
  UseFlip := False;
  InitPlot;
end;

{$IFDEF HASVCL}
procedure InitGraph(var PaintBox: {$IFDEF HASFMX}Vcl.ExtCtrls.{$ENDIF}TPaintBox); {$IFDEF HASFMX}overload;{$ENDIF}
begin
  FrameworkType := fwVCL;
  CMaxY := PaintBox.Height;
  CanvasVCL := PaintBox.Canvas;
  with CanvasVCL do
    begin
      Pen.Color   := clBlack;
      Pen.Style   := psSolid;
      Brush.Color := clWhite;
      Brush.Style := bsSolid;
      FillRect(Rect(0, 0, PaintBox.Width, PaintBox.Height));
      Brush.Style := bsClear;
    end;
  InitParam;
end;
{$ENDIF}

{$IFDEF HASFMX}
procedure InitGraph(var PaintBox: FMX.Objects.TPaintBox); overload;
begin
  FrameworkType := fwFMX;
  CMaxY := Trunc(PaintBox.Size.Height);
  PaintBox.ClipChildren := True;
  CanvasFMX := PaintBox.Canvas;
  with CanvasFMX do
    begin
      Stroke.Color := TAlphaColors.Black;
      Stroke.Kind  := {$IFDEF NEWENUM}TBrushKind.Solid{$ELSE}TBrushKind.bkSolid{$ENDIF};
      Fill.Color   := TAlphaColors.White;
      Fill.Kind    := {$IFDEF NEWENUM}TBrushKind.Solid{$ELSE}TBrushKind.bkSolid{$ENDIF};
      Clear(TAlphaColors.White);
      Fill.Kind    := {$IFDEF NEWENUM}TBrushKind.None {$ELSE}TBrushKind.bkNone {$ENDIF};
    end;
  InitParam;
end;
{$ENDIF}

(***** 座標系を変更する *****)
procedure SetFlipMode(Flip: Boolean);
begin
  UseFlip := Flip;
end;

function FlipY(Y: Integer): Integer;
begin
  if UseFlip then
    Result := CMaxY - Y
  else
    Result := Y;
end;

(***** 描画ルーチン *****)

(* 点を描く *)
procedure Dot(X, Y: Integer);
begin
  case FrameworkType of
{$IFDEF HASVCL}
    fwVCL:
      CanvasVCL.Pixels[X, FlipY(Y)] := CanvasVCL.Pen.Color;
{$ENDIF}
{$IFDEF HASFMX}
    fwFMX:
      CanvasFMX.DrawLine(PointF(X, FlipY(Y)), PointF(X, FlipY(Y)), 1);
{$ENDIF}
  end;
end;

(* 線分を描く *)
procedure Line(X1, Y1, X2, Y2: Integer);
{$IFDEF UseOriginalDrawAlgorithm}
var
  I, DX, DY, S, Step: integer;
begin
  if (X1 < X2) = (Y1 < Y2) then
    Step := 1
  else
    Step := -1;
  DX := abs(X2 - X1);
  DY := abs(Y2 - Y1);
  if DX > DY then
    begin
      if X1 > X2 then
        begin
          X1 := X2;
          Y1 := Y2;
        end;
      Dot(X1, Y1);
      S := DX div 2;
      for I := X1 + 1 to X1 + DX do
        begin
          S := S - DY;
          if S < 0 then
            begin
              S := S + DX;
              Y1 := Y1 + Step;
            end;
          Dot(I, Y1);
        end;
    end
  else
    begin
      if Y1 > Y2 then
        begin
          Y1 := Y2;
          X1 := X2;
        end;
      Dot(X1, Y1);
      S := DY div 2;
      for I := Y1 + 1 to Y1 + DY do
        begin
          S := S - DX;
          if S < 0 then
            begin
              S := S + DY;
              X1 := X1 + Step;
            end;
          Dot(X1, I);
        end;
    end
end;
{$ELSE}
begin
  case FrameworkType of
{$IFDEF HASVCL}
    fwVCL:
      with CanvasVCL do
        begin
          MoveTo(X1, FlipY(Y1));
          LineTo(X2, FlipY(Y2));
        end;
{$ENDIF}
{$IFDEF HASFMX}
    fwFMX:
      CanvasFMX.DrawLine(PointF(X1, FlipY(Y1)), PointF(X2, FlipY(Y2)), 1);
{$ENDIF}
  end;
end;
{$ENDIF}

(* 円を描く *)
procedure Circle(Xcenter, Ycenter, Radius: Integer);
{$IFDEF UseOriginalDrawAlgorithm}
var
  X, Y, S: integer;
begin
  X := Radius;
  Y := 0;
  S := Radius;
  while X >= Y do
    begin
      Dot(Xcenter + X, Ycenter + Y);
      Dot(Xcenter + X, Ycenter - Y);
      Dot(Xcenter - X, Ycenter + Y);
      Dot(Xcenter - X, Ycenter - Y);
      Dot(Xcenter + Y, Ycenter + X);
      Dot(Xcenter + Y, Ycenter - X);
      Dot(Xcenter - Y, Ycenter + X);
      Dot(Xcenter - Y, Ycenter - X);
      S := S - Y * 2 - 1;
      Y := Y + 1;
      if S < 0 then
        begin
          S := S + (X - 1) * 2;
          X := X - 1
        end
    end
end;
{$ELSE}
begin
  case FrameworkType of
{$IFDEF HASVCL}
    fwVCL:
      CanvasVCL.Ellipse(Xcenter - Radius, FlipY(Ycenter - Radius), Xcenter + Radius, FlipY(Ycenter + Radius));
{$ENDIF}
{$IFDEF HASFMX}
    fwFMX:
      CanvasFMX.DrawEllipse(RectF(Xcenter - Radius, FlipY(Ycenter - Radius), Xcenter + Radius, FlipY(Ycenter + Radius)), 1);
{$ENDIF}
  end;
end;
{$ENDIF}

(***** プロッタのシミュレーション *****)

(* プロッタの初期化 *)
procedure InitPlot;
begin
  MoveAbsolute(0, 0);
end;

(* 絶対座標を指定してペン移動する *)
procedure MoveAbsolute(X, Y: Real);
begin
  LastX := X;
  LastY := Y;
end;

(* 絶対座標を指定して線分を描く *)
procedure DrawAbsolute(X, Y: Real);
begin
  Line(Round(LastX), Round(LastY), Round(X), Round(Y));
  MoveAbsolute(X, Y);
end;

(* 相対座標を指定してペンを移動する *)
procedure MoveRelative(X, Y: Real);
begin
  MoveAbsolute(LastX + X, LastY + Y);
end;

(* 相対座標を指定して線分を描く *)
procedure DrawRelative(X, Y: Real);
begin
  DrawAbsolute(LastX + X, LastY + Y);
end;

(* 現在位置を中心として円を描く *)
procedure DrawCircle(R: Real);
begin
  Circle(Round(LastX), Round(LastY), Round(R));
end;

end.

使い方

  1. VCL フォームアプリケーションを新規作成します。
  2. [ファイル | すべて保存] でプロジェクトを適当な場所に保存します。
  3. プロジェクトを保存した場所に uCAGRAPH.pas をコピーします。プロジェクトに追加するかどうかは任意です。
  4. Unit1.pas をコードエディタで開き (表示し)、uses に uCAGRAPH を追記します。

    image.png
  5. フォームに PaintBox を貼り付けます (コンポーネントパレットの [System] タブにあります)。
    image.png
  6. [オブジェクトインスペクタ] の [イベント] タブにある OnPaint イベントをダブルクリックしてイベントハンドラ (PaintBox1Paint) を作ります。
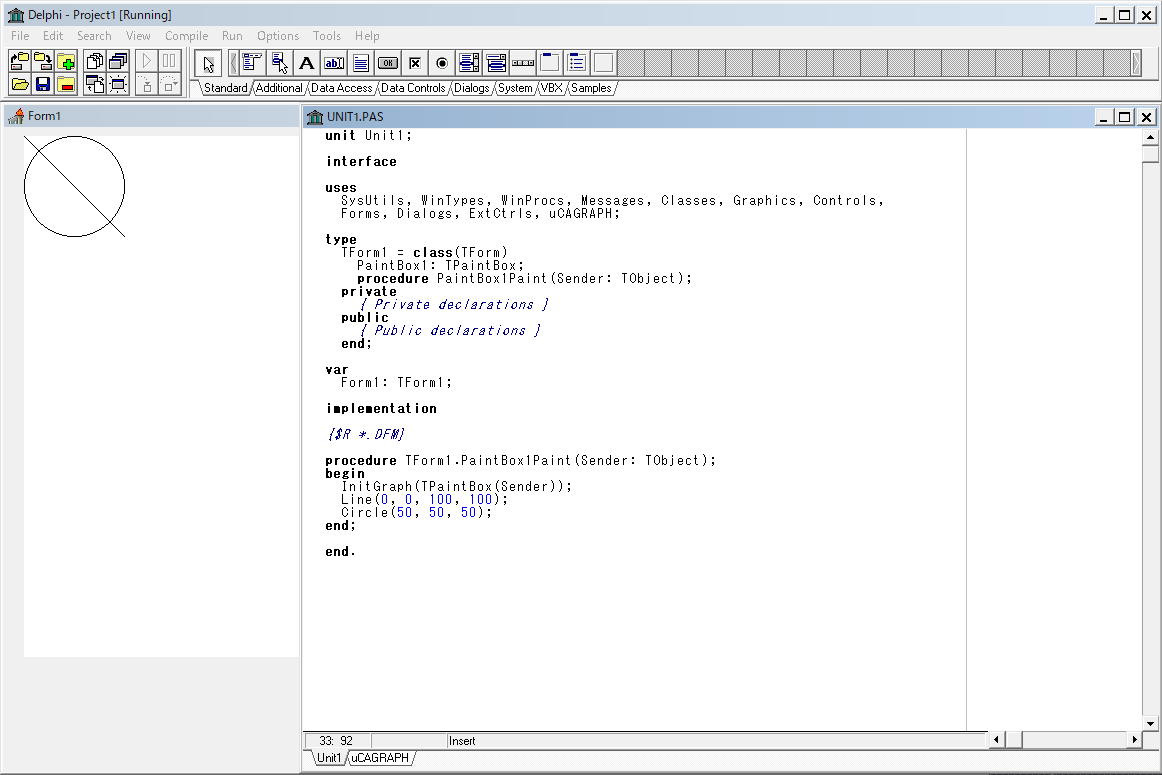
    image.png
  7. イベントハンドラ (PaintBox1Paint) に好きなコードを書きます。

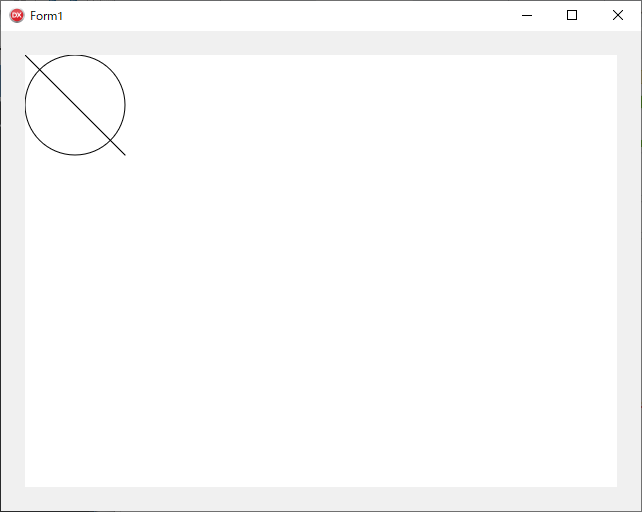
例えば次のようなコードだと

procedure TForm1.PaintBox1Paint(Sender: TObject);
begin
  InitGraph(PaintBox1);
  Line(0, 0, 100, 100);
  Circle(50, 50, 50);
end;

このような図形が描画されます。
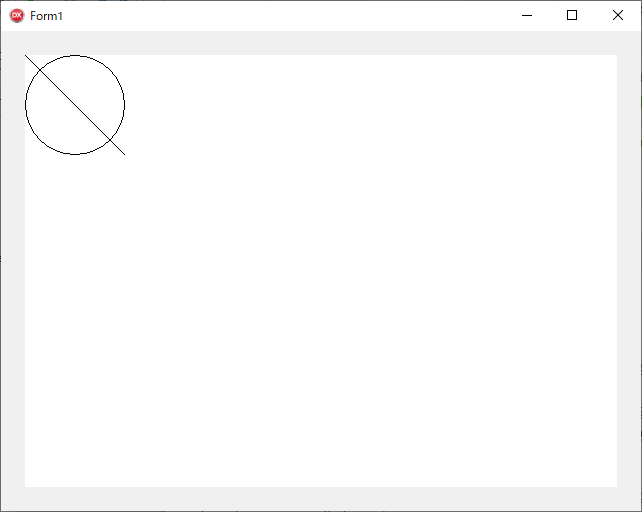
image.png
イベントハンドラ (PaintBox1Paint) の先頭には、貼り付けた PaintBox をパラメータに指定した InitGraph() を記述する必要があります。Sender をキャストしたものを指定しても構いません。

procedure TForm1.PaintBox1Paint(Sender: TObject);
begin
  InitGraph(TPaintBox(Sender)); // 初期化のために必ず追加
  Line(0, 0, 100, 100);
  Circle(50, 50, 50);
end;

uCAGRAPH は FireMonkey フレームワークでも利用可能です。
image.png
VCL とはイベントハンドラのパラメータが異なりますが、中に書くコードは同一となります。

procedure TForm1.PaintBox1Paint(Sender: TObject);                  // VCL
procedure TForm1.PaintBox1Paint(Sender: TObject; Canvas: TCanvas); // FireMonkey

procedure TForm1.PaintBox1Paint(Sender: TObject; Canvas: TCanvas);
begin
  InitGraph(TPaintBox(Sender));
  Line(0, 0, 100, 100);
  Circle(50, 50, 50);
end;

image.png

UseOriginalDrawAlgorithm スイッチ

uCAGRAPH の先頭の方にはコメントアウトされた UseOriginalDrawAlgorithm スイッチがあります。

(*
  {$DEFINE UseOriginalDrawAlgorithm}
*)

この部分をアンコメントすると、Line() や Circle() が『コンピュータアルゴリズム辞典』のアルゴリズムで描画されるようになります。具体的には線分や円がドットで描画されます。
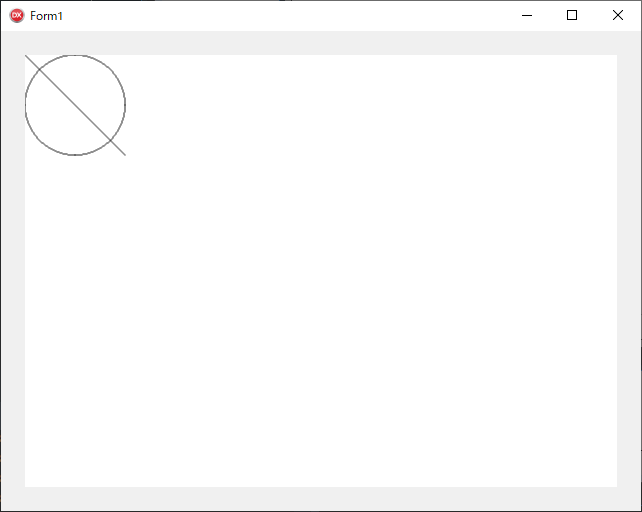
image.png
FireMonkey フレームワークで試してみると円がガタガタになっているのを確認できます。

なぜわざわざ (* *) でコメントアウトしてあるのかというと、Delphi 1 には行コメント (//) が存在しないからです。uCAGRAPH はすべてのバージョンの Delphi で利用可能です 1。
image.png

ギャラリー

ルーチンやプログラムとして記述されているアルゴリズムはイベントハンドラ内の関数内関数として実装します。

『コンピュータアルゴリズム辞典』のコードは、ほぼそのまま利用できます。ソースコードはサポートページから持ってくるといいでしょう。

第 10 章がグラフィック関連なので CHAP10.PRG からコピペして修正 (移植) します。修正の方法についてはギャラリーのソースコードを参考にしてみてください。

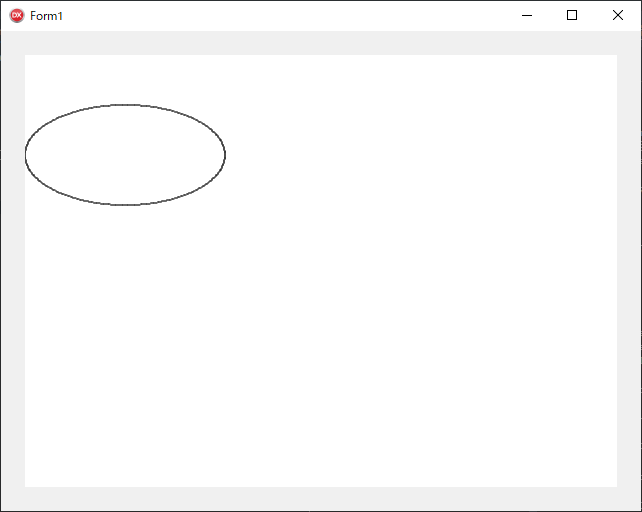
■ 楕円を描く

image.png

procedure TForm1.PaintBox1Paint(Sender: TObject; Canvas: TCanvas);
  (***** 楕円を描く *****)
  procedure DrawEllipse(X, Y, Rx, Ry: real);
  var
    I: integer;
    A: real;
  begin
    MoveAbsolute(X + Rx, Y);
    for I := 1 to 360 do
      begin
        A := I * Pi / 180;
        DrawAbsolute(X + Rx * cos(A), Y + Ry * sin(A))
      end
  end; { DrawEllipse }
begin
  InitGraph(TPaintBox(Sender));
  DrawEllipse(100, 100, 50, 25);
end;

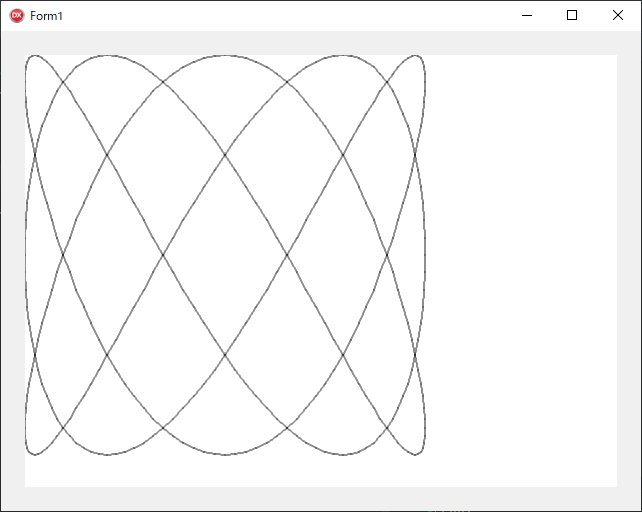
■ リサジュー図形

image.png

procedure TForm1.PaintBox1Paint(Sender: TObject; Canvas: TCanvas);
  (***** リサジュー図形 *****)
  procedure Lissajous(Size: Integer = 500);
  var
    I: integer;
    A: real;
  begin
    MoveAbsolute(Size * 2, Size);
    for I := 1 to 360 do
      begin
        A := Pi * I / 180;
        DrawAbsolute(Size * (cos(3 * A) + 1), Size * (sin(5 * A) + 1))
      end
  end; { Lissajous }
begin
  InitGraph(TPaintBox(Sender));
  Lissajous(200);
end;

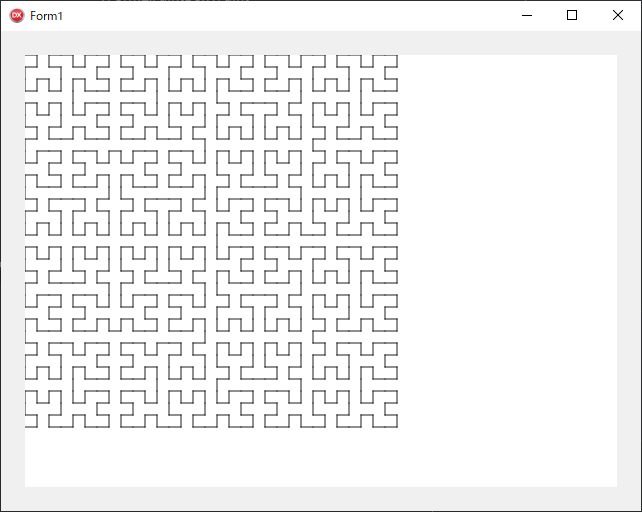
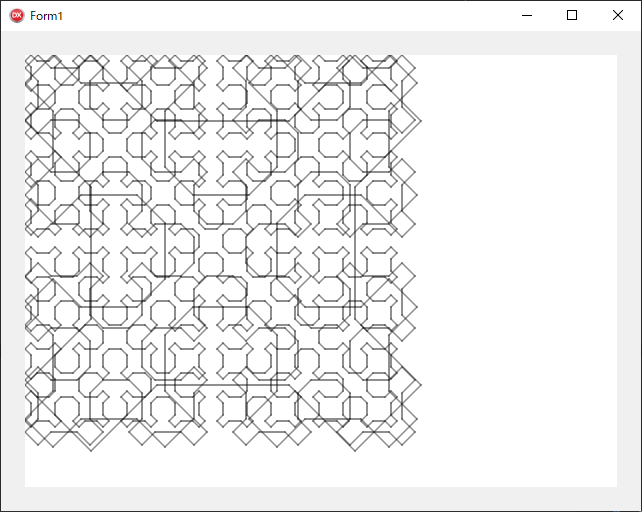
■ ヒルベルト曲線

image.png

procedure TForm1.PaintBox1Paint(Sender: TObject; Canvas: TCanvas);
  (* **** ヒルベルト曲線 **** *)
  procedure Hilbert(Order: Integer = 5; Side: Integer = 1800);
  var
    I, H: integer;

    procedure RUL; forward; (* 互いに他を呼び合う手続きは forward 宣言する *)
    procedure DLU; forward;
    procedure LDR; forward;
    procedure URD; forward;

    procedure RUL;
    begin
      if I > 0 then
      begin
        I := I - 1;
        URD; DrawRelative(H, 0);
        RUL; DrawRelative(0, H);
        RUL; DrawRelative(-H, 0);
        DLU;
        I := I + 1
      end
    end; { RUL }
    procedure DLU;
    begin
      if I > 0 then
      begin
        I := I - 1;
        LDR; DrawRelative(0, -H);
        DLU; DrawRelative(-H, 0);
        DLU; DrawRelative(0, H);
        RUL;
        I := I + 1
      end
    end; { DLU }
    procedure LDR;
    begin
      if I > 0 then
      begin
        I := I - 1;
        DLU; DrawRelative(-H, 0);
        LDR; DrawRelative(0, -H);
        LDR; DrawRelative(H, 0);
        URD;
        I := I + 1
      end
    end; { LDR }
    procedure URD;
    begin
      if I > 0 then
      begin
        I := I - 1;
        RUL; DrawRelative(0, H);
        URD; DrawRelative(H, 0);
        URD; DrawRelative(0, -H);
        LDR;
        I := I + 1
      end { URD }
    end;
  begin
    H := 1;
    for I := 2 to Order do
      H := H * 2 + 1;
    H := Side div H;
    I := Order;
    InitPlot;
    MoveAbsolute(0, 0);
    RUL
  end; { Hilbert }
begin
  InitGraph(TPaintBox(Sender));
  Hilbert(5, 400);
end;

■ シェルピンスキー曲線

image.png

procedure TForm1.PaintBox1Paint(Sender: TObject; Canvas: TCanvas);
  (***** シェルピンスキー曲線 *****)
  procedure Sierpinski(Order: Integer = 4; Side: Integer = 1800);
  var
    I, H: integer;

    procedure URD; forward;
    procedure LUR; forward;
    procedure DLU; forward;
    procedure RDL; forward;

    procedure URD;
    begin
      if I > 0 then
      begin
        I := I - 1;
        URD; DrawRelative(H, H);
        LUR; DrawRelative(2 * H, 0);
        RDL; DrawRelative(H, -H);
        URD;
        I := I + 1
      end
    end; { URD }
    procedure LUR;
    begin
      if I > 0 then
      begin
        I := I - 1;
        LUR; DrawRelative(-H, H);
        DLU; DrawRelative(0, 2 * H);
        URD; DrawRelative(H, H);
        LUR;
        I := I + 1
      end
    end; { LUR }
    procedure DLU;
    begin
      if I > 0 then
      begin
        I := I - 1;
        DLU; DrawRelative(-H, -H);
        RDL; DrawRelative(-2 * H, 0);
        LUR; DrawRelative(-H, H);
        DLU;
        I := I + 1
      end
    end; { DLU }
    procedure RDL;
    begin
      if I > 0 then
      begin
        I := I - 1;
        RDL; DrawRelative(H, -H);
        URD; DrawRelative(0, -2 * H);
        DLU; DrawRelative(-H, -H);
        RDL;
        I := I + 1
      end
    end; { RDL }
  begin
    H := 6;
    for I := 2 to Order do
      H := H * 2 + 2;
    H := Side div H;
    I := Order;
    InitPlot;
    MoveAbsolute(H, 0);
    URD; DrawRelative(H, H);
    LUR; DrawRelative(-H, H);
    DLU; DrawRelative(-H, -H);
    RDL; DrawRelative(H, -H)
  end; { Sierpinski }
begin
  InitGraph(TPaintBox(Sender));
  Sierpinski(1, 400);
  Sierpinski(2, 400);
  Sierpinski(3, 400);
  Sierpinski(4, 400);
end;

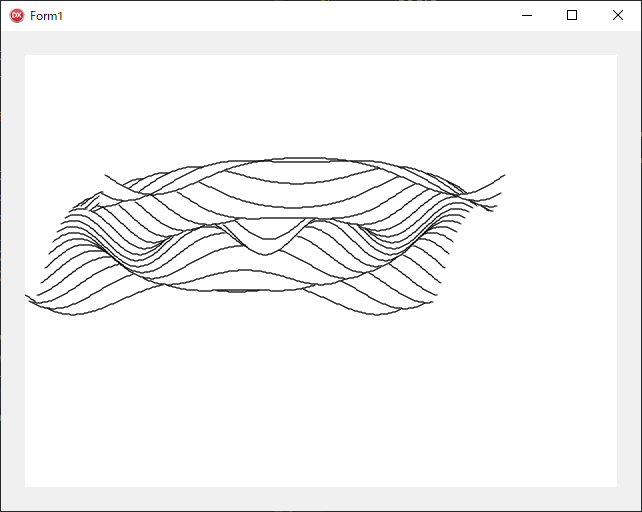
■ ３次元グラフ

image.png

procedure TForm2.PaintBox1Paint(Sender: TObject; Canvas: TCanvas);
(***** ３次元グラフ *****)
  function Func(X, Z: real): real; (* グラフを描きたい２変数関数 *)
  begin
    Func := cos(10 * sqrt(sqr(X) + sqr(Z))) (* 例 *)
  end; { Func }
  procedure FloatingHorizon; (* ３次元グラフを描く手続き *)
  const
    Xmin = -1;
    Xmax = 1;
    Zmin = -1;
    Zmax = 1;
    Yscale = 100;
  var
    X, Z: real;
    I, Ix, Iz, Px, Py: integer;
    Ok, LastOk: boolean;
    LowerHorizon, UpperHorizon: array [0..240] of integer;
  begin
    for I := 0 to 240 do
    begin
      LowerHorizon[I] := maxint;
      UpperHorizon[I] := -maxint
    end;
    for Iz := 0 to 20 do
    begin
      Z := Zmin + (Zmax - Zmin) * Iz / 20;
      LastOk := false;
      for Ix := 0 to 200 do
      begin
        X := Xmin + (Xmax - Xmin) * Ix / 200;
        I := Ix + 2 * (20 - Iz);
        Px := 10 * I;
        Py := round(Yscale * Func(X, Z)) + 30 * Iz + 600;
        Ok := false;
        if Py < LowerHorizon[I] then
        begin
          LowerHorizon[I] := Py;
          Ok := true
        end;
        if Py > UpperHorizon[I] then
        begin
          UpperHorizon[I] := Py;
          Ok := true
        end;
        if Ok and LastOk then
          DrawAbsolute(Px div 5, Py div 5)
        else
          MoveAbsolute(Px div 5, Py div 5);
        LastOk := Ok
      end
    end
  end; { FloatingHorizon }
begin
  InitGraph(TPaintBox(Sender));
  FloatingHorizon;
end;

描画が何か変ですね。どうやら『コンピュータアルゴリズム辞典』は数学の座標系 (右が +X, 上が +Y) を想定しているようです。デフォルトでは画像座標系 (右が +X, 下が +Y) で描画されるので、上下に意味があるものは Y 軸を反転させる必要があります。

begin
  InitGraph(TPaintBox(Sender));
  SetFlipMode(True); // <- 追加
  FloatingHorizon;
end;

SetFlipMode(True); を実行すると Y 軸が反転します。
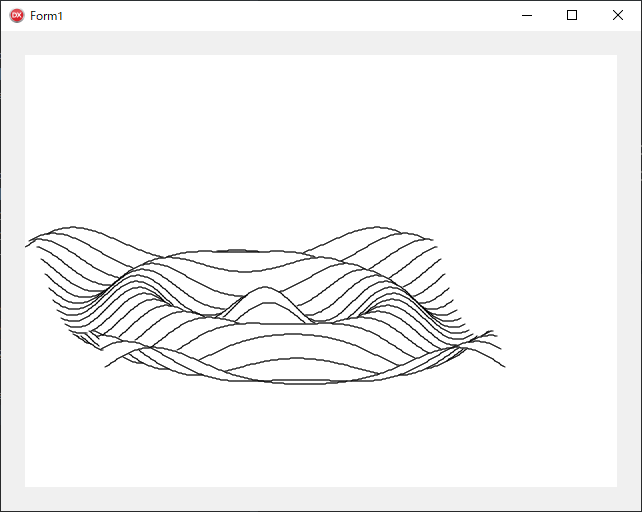
image.png
正しく３次元グラフが描画されました。

■ ローレンツアトラクタ

これは『コンピュータ・アルゴリズム事典』ではなく、同じ著者による『C 言語による最新コンピュータ・アルゴリズム事典』に掲載されていたアルゴリズムです。C 言語で書かれたコードを Pascal に移植してみました。
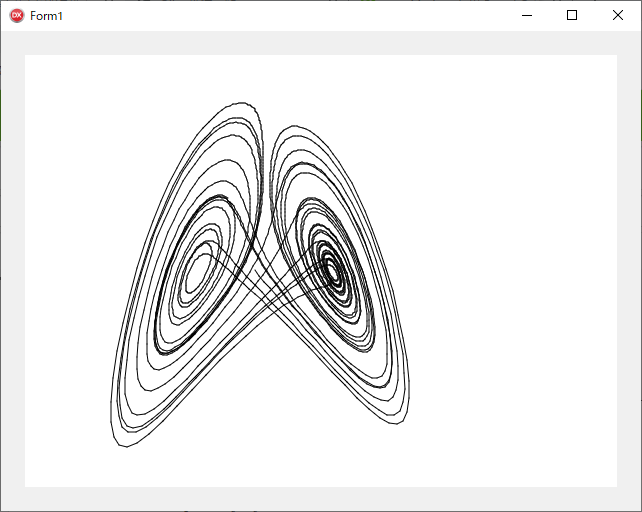
image.png

procedure TForm1.PaintBox1Paint(Sender: TObject; Canvas: TCanvas);
  (***** ローレンツアトラクタ *****)
  procedure Lorenz;
  const
    A = 10.0;
    B = 28.0;
    C = 8.0 / 3.0;
    D = 0.01;
    Scale = 8;
  var
    k: Integer;
    x, y, z, dx, dy, dz: Real;
  begin
    x := 1; y := 1; z := 1;
    for k := 0 to 2999 do
      begin
        dx := A * (y - x);
        dy := x * (B - z) - y;
        dz := x * y - C * z;
        x := x + D * dx;
        y := y + D * dy;
        z := z + D * dz;
        if k > 100 then
          DrawAbsolute((x + 30) * Scale, z * Scale)
        else
          MoveAbsolute((x + 30) * Scale, z * Scale);
      end;
  end; { Lorenz }
begin
  InitGraph(TPaintBox(Sender));
  Lorenz;
end;

image.png

タイトル 著者 ISBN-10
(Amazon)
C 言語による最新アルゴリズム事典 奥村 晴彦 4874084141

書籍に掲載されているソースコードは著者のサイトからダウンロードできます。

ちょっと脱線しますが、『C 言語による最新アルゴリズム事典』で使用されている C コンパイラは Turbo C のようです。Turbo C はアンティークソフトウェアとして Embarcadero のサイトからダウンロード可能です。
image.png

おわりに

Delphi に限ったことではないのですが、ライブラリやフレームワークによって記述方法も異なるため、高機能化した開発言語では単純な図形を描画する事が逆に難しくなっていたりしますよね。

Delphi も VCL と FireMonkey では描画メソッドやプロパティに差異があります。

フレームワーク オブジェクト ドキュメント
VCL Vcl.Graphics.TCanvas DocWiki
FireMonkey FMX.Graphics.TCanvas 2

uCAGRAPH は Android や iOS、macOS 等のプラットフォームでももちろん使えるのですが、クロスコンパイルになるので実用上は...どうなんでしょうね。
image.png

  1. CLX と CLR (.NET) は勘弁してください...orz ↩

  2. XE4 以前は FMX.Types.TCanvas。 ↩

11
4
2

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
11
4