はじめに
Wernerモデルを使った風紋生成のシミュレーションコードを公開しました。この記事では簡単に使い方と動作原理の解説をします。
Wernerモデルとは、Brad Werner (1995) が提案した風紋や砂丘をシミュレーションする方法です。鳥取砂丘で見た風紋がきれいだったので実装してみました。
使い方
--help オプションを参照してください。
$ python simulate.py -h
usage: simulate.py [-h] [-w V] [-g N] [-i N]
options:
-h, --help show this help message and exit
-w V, --wind_speed V wind speed (default: 3.0)
-g N, --grid_size N grid size (default: 100)
-i N, --num_iter N number of iterations (default: 500)
使用例
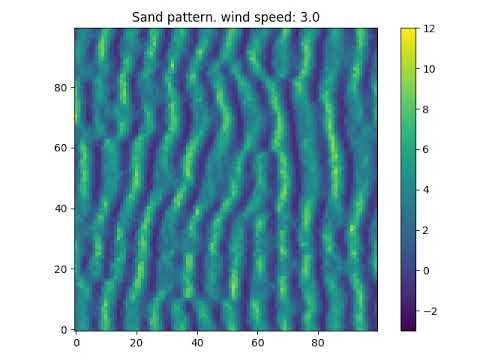
デフォルトで実行すると、風速3.0で計算し、結果を動画ファイルに保存します。風はx方向(左から右)に吹いています。
python simulate.py
計算結果は以下の通りです。風紋のパターンを良く再現しているように見えます。画像をクリックするとYouTubeに飛びます。
デフォルト実行をベースラインとして、風速パラメータを振って模様の変化を見てみます。風が弱い場合にどうなるでしょうか。
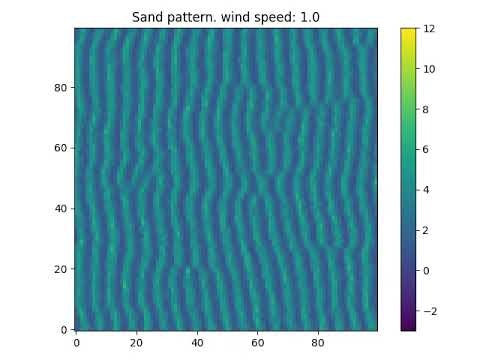
python simulate.py -w 1.0
ベースラインと比較して、波長の短い模様が生成されました。振幅は小さくなるようです。また、模様が生成されるまでの時間も短くなっています。
次に、風が強い場合も実験してみます。
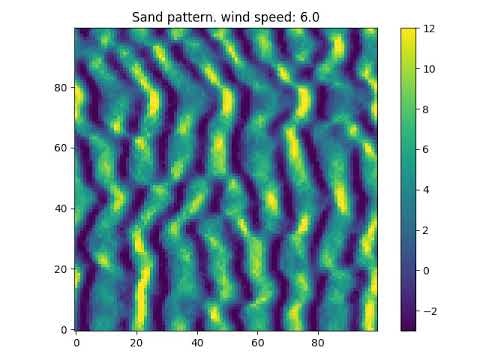
python simulate.py -w 6.0
波長は長く、振幅は大きく、模様が生成されるまでの時間は長くなりました。
動作概要
周期境界条件を設定したグリッドに対して差分法を適用します。次の時間ステップのグリッドを求めるために、2種類のルールを適用します。
for _ in range(num_iter):
grid = apply_jumping_rule(grid, wind_speed)
grid = apply_rolling_rule(grid)
apply_jumping_rule() 関数は、風によって砂が飛ばされる過程を模擬します。以下の現象を考慮しています。
- 高い場所から飛ばされた砂は遠くまで飛ぶ
- 風が強いと遠くまで飛ぶ
apply_rolling_rule() 関数は、砂が崩れる過程を模擬しており、拡散方程式の拡散項に相当する処理です。高さを均一にする効果があります。
詳細はコードを参照してください。
おわりに
Wernerモデルを使った風紋生成のシミュレーションコードの使い方と動作原理の解説をしました。鳥取砂丘で見られる風紋とよく似た模様が生成できました。
2024/1/22 追記:続きの記事 Wernerモデルを使った砂丘の生成 を書きました。