はじめに
極値理論という、あるサンプルの極値(最大値、最小値)がどの様な分布に従うかをモデリングし、パターンを見出そうとする分野が統計学にはあります。この記事では、Rでの実例を紹介しながら、極値理論の金融リスク管理への応用方法を解説していきます。
なお、理論面に関しては、「An Introduction to Statistical Modeling of Extreme Values」(Stuart Coles、2001)を、事例に関しては「Financial risk modelling and portfolio optimization with R, 2nd edition」(Bernhard Pfaff, 2016)の第7章を参考にしました。
その2はこちら。r-block maximaモデルを使った推定を行っています。
https://qiita.com/hrkz_szk/items/2c966aab9342f61a5b59
極値理論とは
極値理論とは統計学の一分野で、分布から大きく外れた値(最大値、最小値)をモデリングする学問です。例えば、とある地点の気温を100年分集め、毎年の最高気温を抽出、100個のサンプルデータを入手し(各気温は互いに独立)、そのデータがどの様な分布に従うのかを推定、またそこから予測等を行っていくというものです(Block maxima法)。このほかにも、一定の閾値を設定し、それを超える値を極値として、その分布を推定する方法もあります(POT法)。こうした推定により、100年に一度の高温はどの程度のものなのか、また500年、1000年に一度の高温も分布から推定が可能になります。異常気象が関連する分野(ダム、堤防の耐久性など)を中心に1920年から発展してきましたが、近年、この考え方をファイナンスに応用することでリスク管理の高度化を図ろうという動きがあります。
一般化極値分布
古典的極値理論によると、極値のパターンを表す確率分布は、Gumbel分布、Frechet分布、Weibull分布の3つのタイプに分類できることが発見されています。

極値理論の初期ではこれら3つから1つ選んで解析を行っていましたが、手元の極値データがどの分布に当てはまるのかを考えるのは相当難しくなります。近年、これら3つの分布が一般化極値分布(GEV:Genelarized Extreme Value distribution)という、次の1つの式で表現できることが発見されました。
$$
G(z)=exp\Big(-1[1+\xi(\frac{z-\mu}{\sigma})^{-\frac{1}{\xi}} ] \Big)
$$
パラメーターは3つで、ロケーションを示す$\mu$(mu)、スケールを示す$\sigma$(sigma)、形を示す$\xi$(xi)となります。今日では上記の式で表せられる一般化極値分布をまず推定し、そこから3つのうちのどれに当たるかを推定するという手法が採られています。具体的には、$\xi\rightarrow0$のときにGumbel分布、$\xi>0$のときにFrechet分布、$\xi<0$のときにWeibull分布となります。上記の3つの分布は、それぞれ、$\xi=0$、$\xi=0.5$、$\xi=-0.5$として作成しました。
パッケージ
実際の使い方の前に、パッケージを紹介します。Rでは極値理論ように様々なパッケージが開発されています。最もメジャーだと思われるのがismevとextRemesです。これらは極値理論の標準的教科書といっていいであろう、「An Introduction to Statistical Modeling of Extreme Values」の本の著者が開発したものです。搭載されているデータもこちらに沿ったもので、この本で学習を進めていくにはもってこいのパッケージです。しかし、この本ではS-PLUSのコードが紹介されている通り、ismevとextRemesとも、Rっぽくないため、慣れるのには一定の時間が必要かと思われます。
このほかにもevirやfExtremesなども有名であり、場合によって使い分けていくのがいいと思います。私はIntroduction-Statistical-Modeling-Springer-Statisticsで勉強をしていたため、ismevとextRemesをよく使っています。ということでまずはパッケージを。
library(ismev)
library(extRemes)
Block maxima モデル
さて、まずは、Rを使ってBlock maximaモデルについて紹介していきたいと思います。Block maximaは10年や50年、100年といった長期スパンでデータを集め、一定期間の最大値や最小値を抽出し、それらがどのように分布しているのかを解析する方法です。このモデルの良いところは、一定期間という区切りを設けているため、それぞれの値が互いに独立であるという条件を満たしやすいというところにあります。
データ
ここでは、シーメンスの株価の損失について、半年ごとの期間の最大値を抽出し、一般化極値分布への推定を行います。データに関しては、evirというパッケージにあるdata(siemens)を使用します。こちらは1973年1月2日から1996年7月23日におけるsiemens社の株価のログリータンがvectorで入っています。
library(evir)
data(siemens)
head(siemens)
## [1] 0.014347448 0.010861972 0.007020857 0.001863933 0.000000000 -0.001397624
simensに格納されている時系列データを抽出し、simensを時系列データ化するとともに、100をかけてパーセント表示に。
SieDates <- as.character(format(as.POSIXct(attr(siemens, "times")), "%Y-%m-%d"))
SieRet <- timeSeries(siemens * 100, charvec = SieDates)
plot(SieRet, ylab="Log-return of Siemens")

損失
今回はリスク管理という観点から、どれだけ大きな損失が発生するかを見ていきたいので、ログリータンをプラスの損失に変換します。また、100をかけてパーセント表示に変換します。
SieLoss <- -1*siemens*100.0
head(SieLoss)
## [1] -1.4347448 -1.0861972 -0.7020857 -0.1863933 0.0000000 0.1397624
最大値の抽出
evirパッケージにあるgevを使うとGEV(一般化極値分布)へ当てはめを行ってくれるのですが、ここでは当てはめではなく、最大値を抽出するために使っていきたいと思います。先に述べたように、ここでは半年間の最大値をそれぞれ抽出し、それらをGEVに当てはめていきますの。gevでは当てはめるデータがPOISXct形式の日時データで格納している場合、block="semester"とすることで、半年間の最大値を自動的に抽出し、それらのデータをGEVに当てはめてくれます。SieGEV$dataに抽出した半年ごとの最大値が格納されています。
SieGEV <- gev(SieLoss, block = "semester")
SieMaxima <- SieGEV$data
head(SieMaxima)
## [1] 3.519720 3.589676 3.425749 3.187262 2.768500 1.839737
サンプルの分布
plotを使ってビジュアライズ。横軸が時間を表していて、10であれば5年目、20であれば10年目となります。縦軸はその期間の最大損失値です。
plot(SieGEV$data, type = "h", xlab = "",
ylab = "Block Maxima", main = "Maximum Biannual Losses of Siemens")

GEVへの当てはめ
extRemesのfevdを使います。type = "GEV"とすることで一般化極値分布へのあてはめを行ってくれます。
fitgev <- fevd(SieMaxima, type = "GEV")
fitgev
##
## fevd(x = SieMaxima, type = "GEV")
##
## [1] "Estimation Method used: MLE"
##
##
## Negative Log-Likelihood Value: 85.95227
##
##
## Estimated parameters:
## location scale shape
## 2.6998887 1.0468771 0.2867664
##
## Standard Error Estimates:
## location scale shape
## 0.1697813 0.1413925 0.1171486
##
## Estimated parameter covariance matrix.
## location scale shape
## location 0.02882568 0.014747592 -0.005123580
## scale 0.01474759 0.019991843 0.001016437
## shape -0.00512358 0.001016437 0.013723786
##
## AIC = 177.9045
##
## BIC = 183.5182
推定結果
主要なデータを取り出しつつ、推定結果を見ていきます。extRemesはRっぽくないと冒頭述べましたが、GEVデータの抽出はdistillを使います。
distill(fitgev)
## location scale shape nllh
## 2.699888719 1.046877147 0.286766363 85.952273791
## location.location scale.location shape.location location.scale
## 0.028825684 0.014747592 -0.005123580 0.014747592
## scale.scale shape.scale location.shape scale.shape
## 0.019991843 0.001016437 -0.005123580 0.001016437
## shape.shape
## 0.013723786
パラメータ
$\xi$(shape)がプラスなので、今回の分布はFrechet分布に従うことが分かります。このため、この分布はヘビーテイルであり、損失が有限ではないということになります。
par.gev <- distill(fitgev)[1:3]
par.gev
## location scale shape
## 2.6998887 1.0468771 0.2867664
尤度
loglik.gev <- distill(fitgev)[4]
loglik.gev
## nllh
## 85.95227
標準誤差
まずはdistillから共分散行列を取り出し、その対角成分を抽出、その後ルートにして標準誤差に直します。
# variance-covariance
cov.gev <- matrix(as.numeric(distill(fitgev)[5:13]),nrow = 3, byrow = T,
dimnames =list(c("location","scale","shape"),
c("location","scale","shape")))
# Standard errors
se.gev <- sqrt(diag(cov.gev))
se.gev
## location scale shape
## 0.1697813 0.1413925 0.1171486
パラメータの検証
信頼区間
すべてのパラメータがゼロをまたいでいないので、どれもゼロではないと言えます。
ci.fevd(fitgev, type = "parameter")
## fevd(x = SieMaxima, type = "GEV")
##
## [1] "Normal Approx."
##
## 95% lower CI Estimate 95% upper CI
## location 2.36712352 2.6998887 3.0326539
## scale 0.76975291 1.0468771 1.3240014
## shape 0.05715939 0.2867664 0.5163733
プロファイル尤度
一般化極値分布への当てはめで最も大切なのは$\xi$(shape)になります。$\xi$のみで尤度を計算し、プロットすると次のようになります。ここでも95%信頼区間はゼロをまたいではいません。
profliker(fitgev, type = "parameter", which.par = 3, xrange = c(-0.1,0.5))
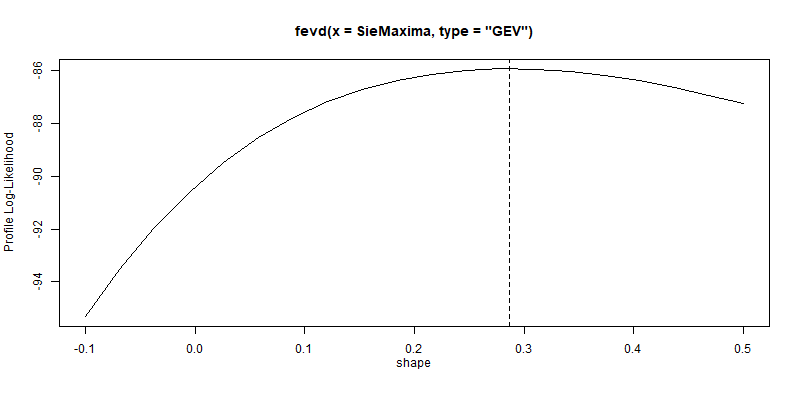
ci.fevd(fitgev, type = "parameter", which.par = 3, method = "proflik")
## fevd(x = SieMaxima, type = "GEV")
##
## [1] "Profile Likelihood"
##
## [1] "shape: 0.287"
##
## [1] "95% Confidence Interval: (0.1095, 0.4627)"
再現レベル
推定された分布から、損失額の再現レベルが分かります。約6%の損失が10年に一度、約13%の損失が100年に一度起こるという推定結果になります。
profliker(fitgev, type = "return.level", return.period = 10, xrange = c(4.2, 9.0))

ci.fevd(fitgev, type = "return.level", return.period = 10)
## fevd(x = SieMaxima, type = "GEV")
##
## [1] "Normal Approx."
##
## [1] "10-year return level: 6.01"
##
## [1] "95% Confidence Interval: (4.5703, 7.449)"
profliker(fitgev, type = "return.level", return.period = 100, xrange = c(4.2, 9.0))

ci.fevd(fitgev, type = "return.level", return.period = 100)
## fevd(x = SieMaxima, type = "GEV")
##
## [1] "Normal Approx."
##
## [1] "100-year return level: 12.704"
##
## [1] "95% Confidence Interval: (5.6108, 19.7967)"
なお、実際のデータの最大損失は、
mLoss <- max(SieGEV$data)
mLoss
## [1] 12.01116
12.1%です。これがどの程度の頻度で発生するかは、次のコードから分かるように約42年周期となります。
mYears <- 1 / (1 - pevd(mLoss, loc=par.gev[1], scale=par.gev[2], shape=par.gev[3])) / 2
mYears
## [1] 41.74189
モデルの検証
plot.fevd で推定結果の様々なグラフをプロットすることが出来ます。ここではメジャーな4つを紹介します。
par(mfrow=c(2,2))
plot.fevd(fitgev, type = "probprob", main="Probability plot")
plot.fevd(fitgev, type = "qq", main="Quantile plot")
plot.fevd(fitgev, type = "rl", main="Return level plot")
plot.fevd(fitgev, type = "density", main="Density plot")

Probability PlotとQuantilte Plotとともに右上の方がラインに沿っておらず、推定したモデルでは説明しきれていないことを示しています。Return level plotではそれぞれの値が95%以内には収まっていることを示しています。また、このグラフから、この推定されたモデルでは7~8%の損失が10年に一回発生するとしていることが分かります。Density Plotはサンプルデータと推定モデルが概ね一致していること、右の裾野が延々と広がっていることが分かります。
続編
その2はこちら。r-block maximaモデルを使った推定を行っています。
https://qiita.com/hrkz_szk/items/2c966aab9342f61a5b59

