はじめに
令和元年の台風19号の被害が凄いことになっていますが、様々な河川の氾濫が報道されています。気候変動の影響があり、今回のような規模の水害は想定できなかったという意見も聞こえてきますが、本当にそうなのかと素人ながら疑問に思っていました。というのも、堤防を作る際に、異常降水を外れ値とみなして削除して計算しているということも耳にしたからです。
そんなわけで、今回は異常値を外れ値とはみなさない極値理論を用いて、今回の氾濫が推定できたのか検証してみました。
<やったこと>
PythonのBeautiful Soupを使ったスクレイピング
RのAmeliaを使った多重代入法による時系列分析の欠損値補完
RのismevとextRemesを使った極値理論解析
<環境>
Windows Subsystem for Linux
Ubuntu 18.04
Python 3.6
R 3.6.0
極値理論とは
Block Maxima法
極値理論とは統計学の一分野で、分布から大きく外れた値(最大値、最小値)をモデリングする学問です。例えば、とある地点の気温を100年分集め、毎年の最高気温を抽出、100個のサンプルデータを入手し(各気温は互いに独立)、そのデータがどの様な分布に従うのかを推定し、またそこから今後500年間に発生するであろう最高気温を予測するというものです(Block maxima法)。個々での肝は、利用可能なデータを用い、長期間で発生するであろう人類が経験したことないような現象を予測するということです(外挿)。
Peak Over Threshold法
しかしながら、この手法ではサンプル数が多く集められず、精度の良いモデリングができないという致命的な欠点があります。そこで、近年はその課題を克服した、Peak Over Threshold法(POT法)という手法が最近になって登場し、現在では、極値理論と言えば、こちらを指すようになりました。このPOT法では、極値が従う分布を調べる代わりに、一定の閾値を超える値(ピーク)を設定し、一般パレート分布をピークデータに当てはめて解析するものです。この背景には、ピークが従う確率分布は元の分布によらず一般化パレート分布で近似できるというのがあります (Pickands–Balkema–de Haan定理)。また、Block maxima法よりもサンプル数が増えるため、推測の精度が良くなります。
一般化パレート分布
一般化パレート分布はGP($\sigma, \xi$)で表され、次の式になります。
$$
H(y)=1-(1+\xi \frac{y}{\sigma})^{-1/\xi}
$$
パラメーターは2つで、スケールを示す$\sigma$(sigma)、形状を示す$\xi$(xi)となります。この形状パラメーターは、$\xi>0$のときには超過損失の上限があり、$\xi<0$のときには超過損失の上限がないということになります。そして$\xi\rightarrow0$でリミットを取るときは
$$
H(y)=1-exp(-\frac{y}{\sigma})
$$
と標記でき、パラメーターが$-\frac{1}{\sigma}$の指数分布になります。次のグラフは一般パレート分布の確率密度関数で、$\sigma$=1とし、$\xi$を色々変えてプロットしたものです。

まぁ、簡単に言えば、分布の右のすそ野を精緻に推定したという感じでしょうか。これにより、ほとんど起こらないにしても、もの凄く大きい損失が発生し得るというものが存在するというイメージです。この一般パレート分布を使った推定を今回はやって行こうと思います。
データ
今回使用したのは、氾濫危険水位を超えた多摩川にある田園調布(上)観測所の水位データ。データは水文水質観測所情報にある時刻水位月表を使用。1930年からの毎時間のデータが格納されていたので少しだけ驚きました。ただ、データがこんな形で、月単位でしか表示されず、これを手で拾っていたら膨大な時間を失いかねないと思ったので、ページの構造も単純であったこともあり、スクレイピングをして、データを拾いました。
スクレイピング
ライブラリ
# スクレイピング用のライブラリ
import requests
from bs4 import BeautifulSoup
# 基本ライブラリ
import pandas as pd
対象リンク一覧
月単位で表示されるページのURL
ですが、構造としては
http://www1.river.go.jp/cgi-bin/DspWaterData.exe?KIND=2&ID=303051283310030&BGNDATE=-
19300101←検索したい年月日 &ENDDATE=20191231&KAWABOU=NO
という3つの構造に区切られるので、上下二つは固定して、真ん中を19300101から20191001まで準備して、リンク一覧を作成。これはエクセル(links_kami.csv)でやりました。で、できたのがこちら。
links = pd.read_csv('links_kami.csv')
links.link[0]
'http://www1.river.go.jp/cgi-bin/DspWaterData.exe?KIND=2&ID=303051283310030&BGNDATE=20191001&ENDDATE=20191231&KAWABOU=NO'
links.link[1]
'http://www1.river.go.jp/cgi-bin/DspWaterData.exe?KIND=2&ID=303051283310030&BGNDATE=20190901&ENDDATE=20191231&KAWABOU=NO'
links.links[2]
'http://www1.river.go.jp/cgi-bin/DspWaterData.exe?KIND=2&ID=303051283310030&BGNDATE=20190801&ENDDATE=20191231&KAWABOU=NO'
スクレイピング用の関数
以下の関数を用いて、ウェブページに表示されているテーブルをpandasのデータフレーム形式で抽出します。
def get_data(url):
target_url = url
r = requests.get(target_url)
soup = BeautifulSoup(r.text, 'lxml')
row_list = soup.find_all('tr')
data = pd.DataFrame(row_list[3].text.split('\n')[1:-1])
# 最終的にはpd.DataFrame形式で対象となる月のデータを抽出
# row_list[3]がカラムのタイトルなので、これをベースに
for i in range(4,len(row_list)-1):
list_24 = []
# それぞれの日付ごとに、1時~24時までのデータを格納するリスト
list_24.append(row_list[i].find('th').text) # 縦に移動し、日付を抽出
for j in range(24):
water_level = row_list[i].find_all('td')[j].text #横に移動し水位データを抽出
if water_level == '閉局': #'閉局'の場合は欠損値に
list_24.append('NA')
elif water_level == '欠測': #'欠測'の場合は欠損値に
list_24.append('NA')
elif water_level == '\u3000': #'空欄'の場合は欠損値に
list_24.append('NA')
else:
list_24.append(float(water_level))
data_24 = pd.DataFrame(list_24) #pandasのデータフレームに
data = pd.concat([data, data_24], axis=1) #大元のデータフレームと結合
data = data.transpose().iloc[1:,:] #カラムタイトルを削除
return data
データ抽出
各月ごとにウェブページからデータを引っ張ってきつつ、それぞれ結合し
raw_data = get_data(links.iloc[0,:][0]) #ベースとなるデータを最初に
for i in range(1,links.shape[0]):
each_data = get_data(links.iloc[i,:][0])
raw_data = pd.concat([raw_data, each_data])
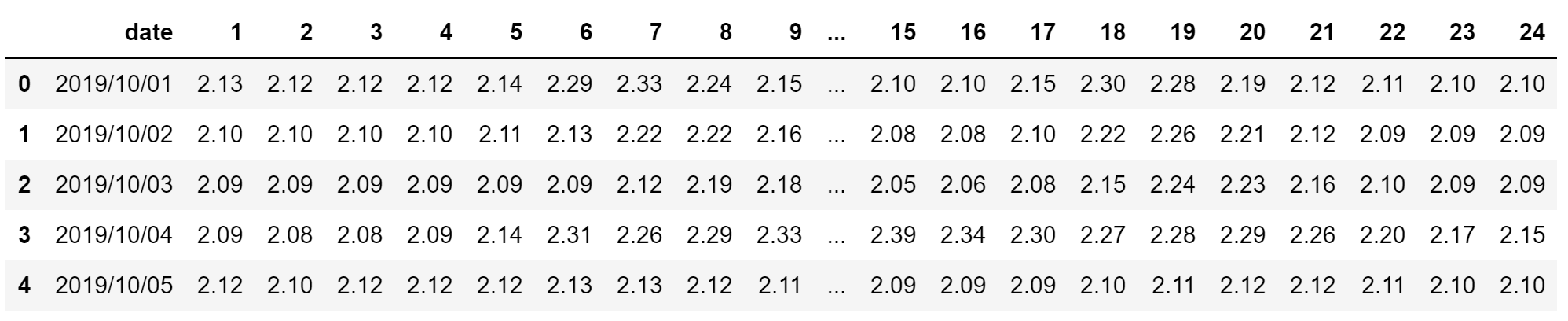
raw_data.head(2)
Wide to Long
raw_data.columns = ["date", 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]
raw_data.head()
meltを使ってwide型からlong型に
data = pd.melt(raw_data ,id_vars='date', var_name='hour', value_name='level')
data = data.sort_values(['date','hour']).reset_index(drop = True)
data.head()

data.to_csv("data.csv", index = False)
保存して終了。続きはRで。
データ整形
Rで読み込み
raw_data = read.csv("data.csv", header = TRUE)
head(raw_data)

時間形式に変換
date <- strptime(x = as.character(raw_data$date), format = "%Y/%m/%d")
hour <- sprintf("%02d:00",raw_data$hour)
time_index <- as.POSIXct(paste(date, hour), format="%Y-%m-%d %H:%M")
data <- raw_data
data$date <- time_index
data$hour <- NULL
head(data)

可視化
plot(y=data$level, x=data$date, type = "l",
ylab = "water level", xlab = "date")
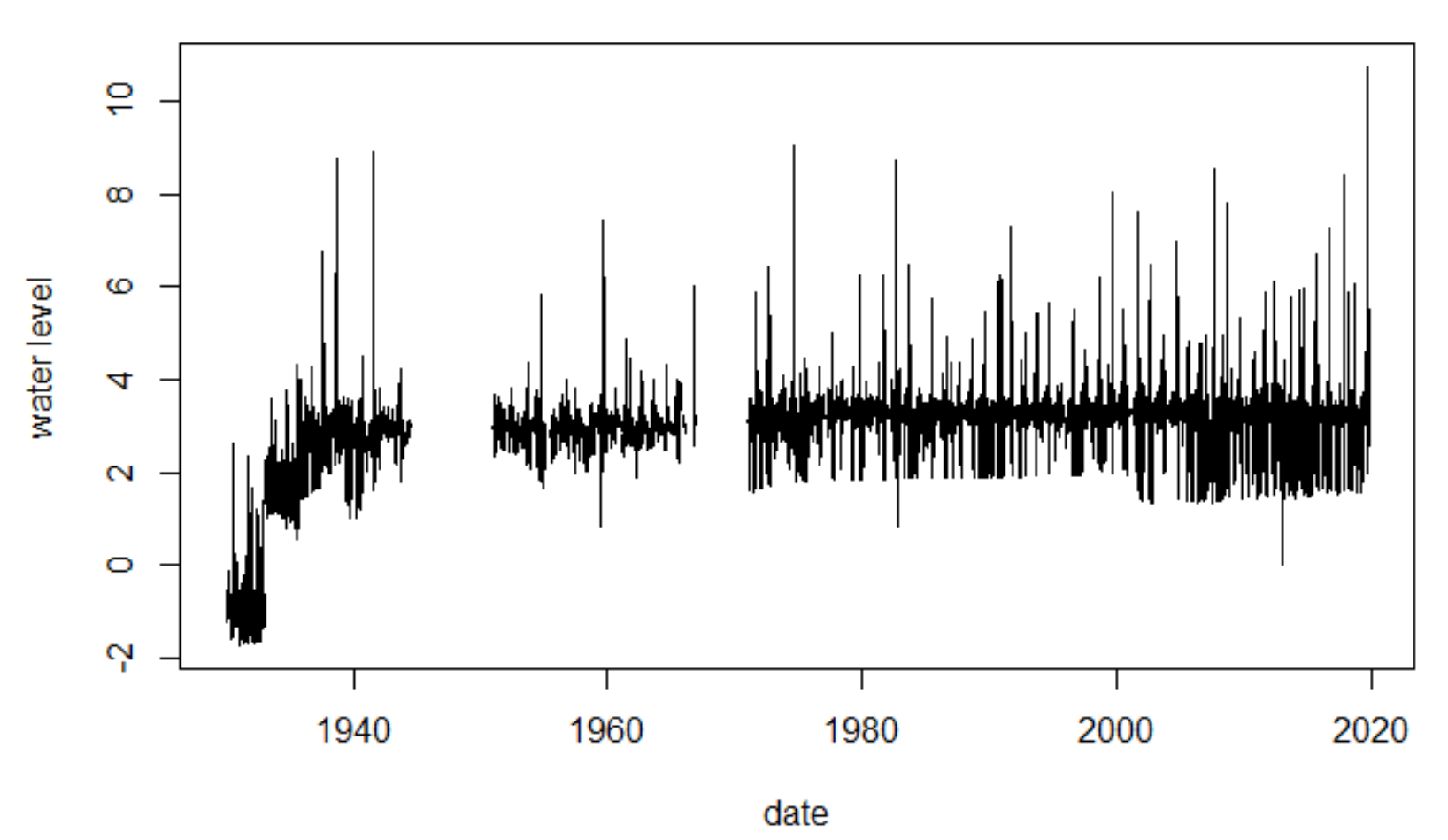
1930~1940年半ばのデータに関しては、測量方法が異なるのか、マイナスになっている…。極値理論で用いるデータは定常過程なのが望ましいので、一番初めのブロックのデータは今回は用いないことに。この辺り、水文学の知識が欲しいですね…。
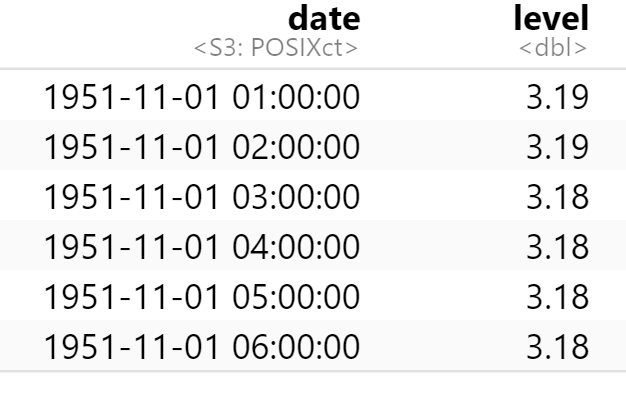
target_date = "1951-11-01 01:00:00"
plot(y=data[data$date >= target_date,]$level,
x=data[data$date >= target_date,]$date,
type = "l", ylab = "water level", xlab = "date")

なお、1951年11月からデータを採っていますが、今回は2019年10月までを対象とすることを念頭に置いていて、一年単位とするためです。ということでデータを分割。
new_data <- data[(data$date >= target_date)&(data$date <= "2019-10-25"),]
rownames(new_data) <- NULL
head(new_data)

理由は分かりませんが、なぜか冒頭4つがNAに…。これも削除。
new_data <- new_data[5:dim(new_data)[1],]
head(new_data)

欠損値の補完
さて、グラフを見て明確なのですが、水位置に欠損値が沢山あります。
sum(is.na(new_data$level))
dim(new_data)
62139/595920 * 100
[1] 62139
[1] 595920 2
[1] 10.42741
全体の10.4%!欠損値をすべて削除するにはかなりの大きな数なので、多重代入法を使って補完していきたいと思います。Rで多重代入法と言えばのAmelia。normやmiceだとデータのトレンドを反映させることが出来ないおそれがあるためです。
library(Amelia)
ameliaで時系列データを扱う場合、tsは時系列データの単位を指定します。また、leadsで補完する時点の先の値を変数として導入できます(予測モデルではなく因果モデルであるため)。そして、polytimeでトレンドの多項式を指定できます。今回、設定したものを数式で書くと以下のようになります。
$$
level_t = \beta_0 + \beta_1 level_{t-2} + \beta_2 level_{t-1}
+ \beta_3 level_{t+1} + \beta_4 level_{t+2}
+ \beta_5 t + + \beta_6 t^2 + \beta_7 t^3
$$
M <- 5
set.seed(1)
a.out <- amelia(new_data, m=M, ts="date", lags = "level", polytime = 3, leads = 2)
impX <- matrix(NA, nrow(new_data), M)
for(i in 1:M){
imp1 <- data.frame(a.out$imputations[i])[2]
for(j in 1:nrow(new_data)){
impX[j,i] <- imp1[j,]
}
}
impdata <- data.frame(impX)
head(impdata)

M<-5としたの5つの補完後のデータが入手できました。今回はこれの平均値を最終的な補完データとして行きたいと思います。
meanimpdata <- rowMeans(impdata)
impdata <- data.frame(new_data$date, meanimpdata)
colnames(impdata) <- c("date", "level")
head(impdata)
sum(is.na(impdata))
[1] 0
もちろん、欠損値はなし
可視化
plot(y=impdata$level, x=impdata$date,
type = "l", ylab = "water level", xlab = "date")
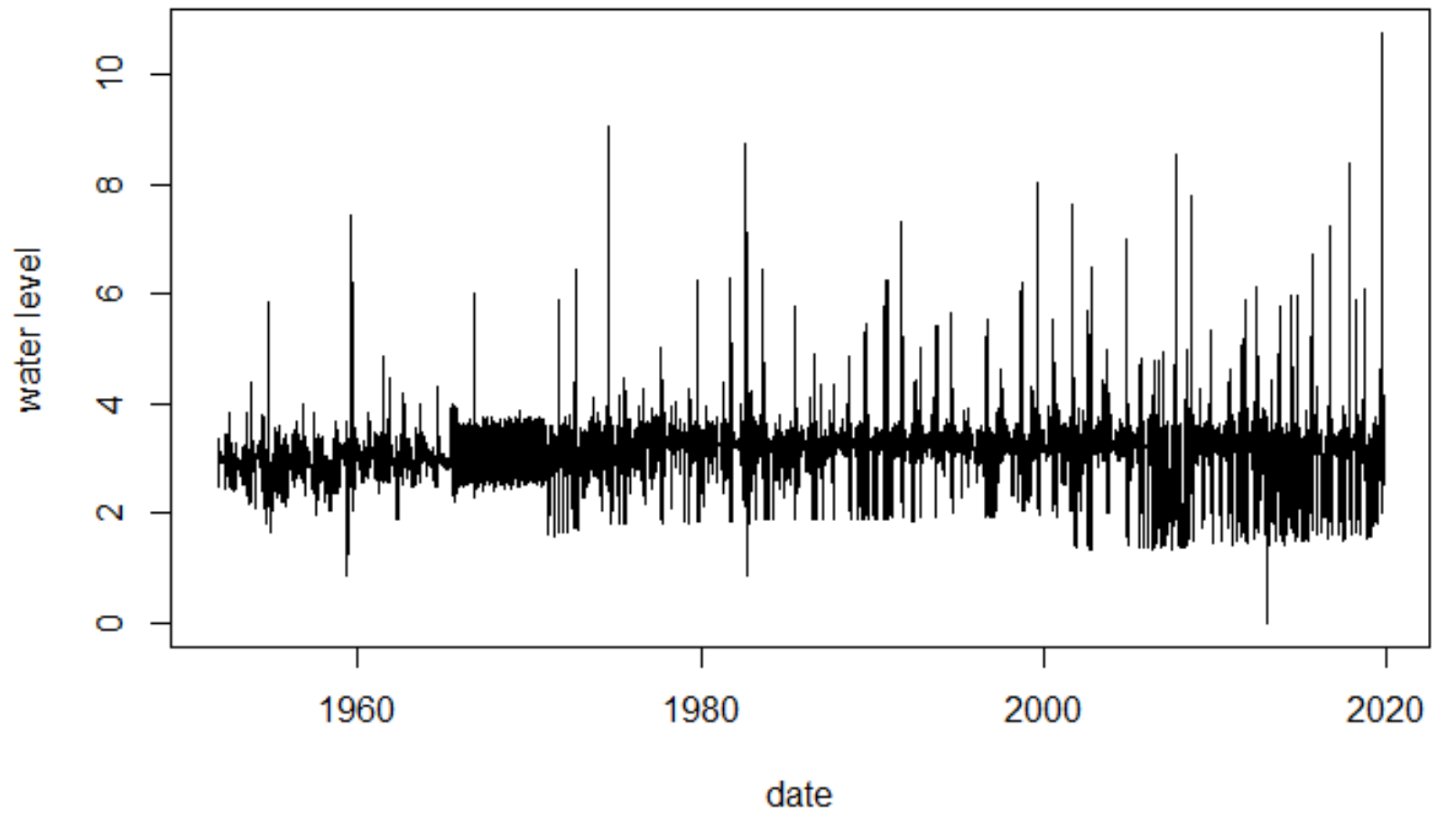
1970年代が適切に補完されているのか疑問は残りますが、極値理論では一定程度を超える値のみを扱っていきますので、今回は気にせずにこのまま進めていきましょう。
さて、長くなりましたが、ようやく極値解析できるところまで到達しました…。
データ分割
極値解析の前に、データを台風19号の影響がないものとあるものに分けて、解析をそれぞれ進めていきたいと思います。台風19号の影響がどれだけのものかを最終的には見ていこうとかと。
before_data <- impdata[impdata$date <= "2019-10-6",]
after_data <- impdata
plot(y=before_data$level, x=before_data$date, type = "l")

plot(y=after_data$level, x=after_data$date, type = "l")
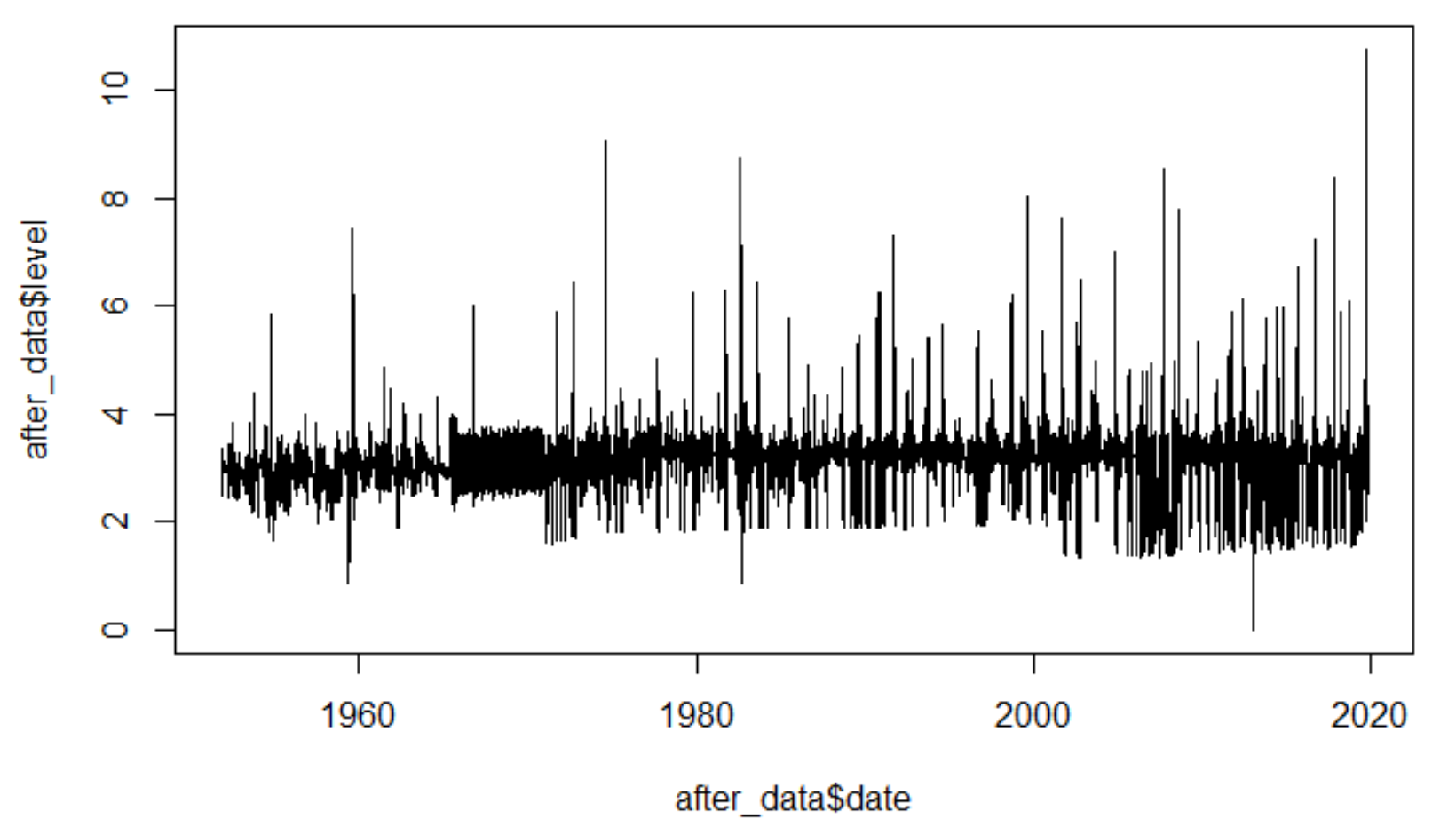
直近の10M超が目立ちますね。
極値解析
RでPOT法が使えるライブラリはいくつかありますが、今回はismevとextRemesを使っていきます。ismevは極値理論の標準的な教科書であるAn Introduction to Statistical Modeling of Extreme Values」(Stuart Coles、2001)の著者が作成したものです。またextRemesは時間の単位を調整してくれるので、今回はこちらも使っていきます。
library(ismev)
library(extRemes)
閾値の設定
Thresholdモデルで重要なのが閾値をどのように選ぶかという点です。閾値が高すぎるとサンプル数が減ってしまい、標準誤差が大きくなってしまいますが、逆に低すぎるとモデルのバイアスが高くなってしまうというトレードオフの関係があります。ただ、慣例としてはできるだけ低く設定し、サンプル数を増やすということが行われています。
mrl.plot(before_data$level)
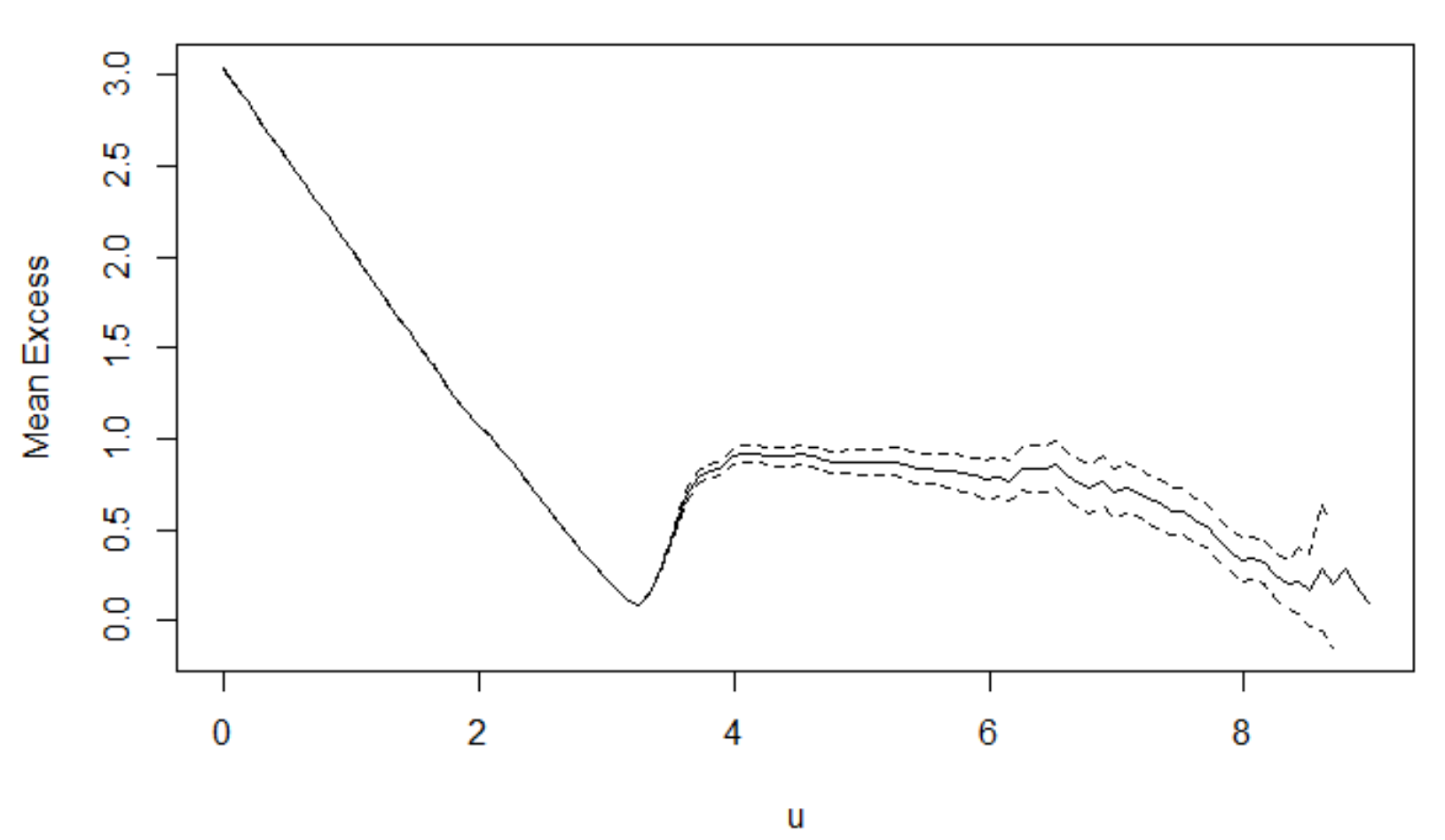
このグラフの解釈の仕方ですが、綺麗な線形状になっていて、95パーセンタイルの幅がそこまで広くなりすぎていないところを選択します。ここでは6を閾値として選択したいと思います。かなり主観的ではありますが…、色んな文献で指摘されています…。
「An Introduction to Statistical Modeling of Extreme Values」で言われている別の方法が、何種類かの閾値を用いてGPD推定を行い、パラメーターの標準誤差を比較し、比較的標準誤差の低い中で、最大の閾値を用いたモデルを選択するというものです。ここでは上記のMRLを踏まえて、4~8の閾値を用いて、二つのパラメータとその95パーセンタイルを求めます。
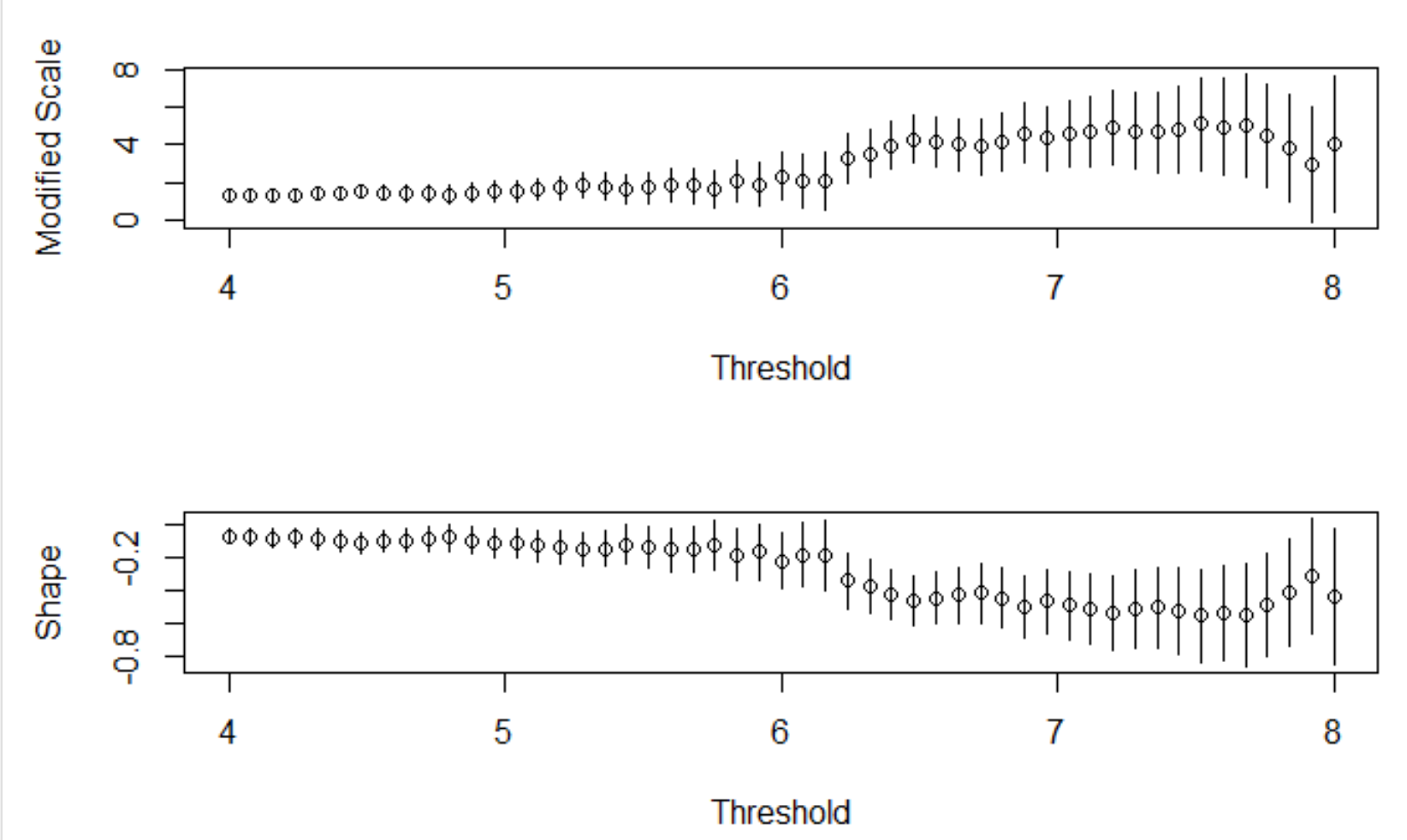
やはり6あたりから幅が広くなっているので、6を閾値とします。
u <- 6
また、プロットして確認したのが、こちらです。
col.exceed <- before_data$level
col.exceed[col.exceed > u] <- "red"
col.exceed[col.exceed <= u] <- "black"
plot(before_data$level, pch=20, ylab="water level", col=col.exceed)
abline(h=u)

推定
一般パレート分布に当てはめる前に、before_dataが一年間にいくらのデータを持つかを確認します。
range(before_data$date)
2019 - 1951 + 1
dim(before_data)
595464 / 69
[1] "1951-11-01 01:00:00 JST" "2019-10-06 00:00:00 JST"
[1] 69
[1] 595464 2
[1] 8629.913
そしてextRremesのfevdで推定。type = "GP"としてあげればよしです。
before_fit <- fevd(level, before_data, threshold = u, type = "GP",
time.units = "8730.122/year")
パラメータ検証
scale=0.9993629で、shape=-0.2192457。いずれも95%信頼区間を反対の符号をまたいでいません。
ci(before_fit, type = "parameter")
fevd(x = level, data = before_data, threshold = u, type = "GP",
time.units = "8730.122/year")
[1] "Normal Approx."
95% lower CI Estimate 95% upper CI
scale 0.7738166 0.9993629 1.22490914
shape -0.3935938 -0.2192457 -0.04489764
モデル検証
plot(before_fit)
 左上のqqプロットの当てはまりもよさそうなので、一先ずはこのモデルで良さそうです。
左上のqqプロットの当てはまりもよさそうなので、一先ずはこのモデルで良さそうです。
再現レベル
推定された分布から、水位の再現レベルが分かります。
return.level(before_fit, return.period = c(10, 50, 100), do.ci=TRUE)
fevd(x = level, data = before_data, threshold = u, type = "GP",
time.units = "8629.913/year")
[1] "Normal Approx."
95% lower CI Estimate 95% upper CI
10-year return level 7.909737 8.328664 8.747590
50-year return level 8.276751 8.991559 9.706367
100-year return level 8.338449 9.212431 10.086412
10年に一度のレベルが$(7.9, 8.7)$、50年に一度のレベルが$(8.3, 9.7)$、100年に一度のレベルが$(8.3, 10.1)$という感じに解釈するので(いずれも単位はメートル)、今回の10Mを超える水位については、少なくとも100年に一度のレベルということになります。なお、95%信頼区間ではなく、推定値自体が10Mを超えるのは、10,000年に一度という推定結果になりました…。
台風19号後のデータの再現レベル
after_dataについても上記と同じ極値分析を行いました。こちらは再現レベルの結果だけ載せておきます。
return.level(after_fit, return.period = c(10, 50, 100), do.ci=TRUE)
fevd(x = level, data = after_data, threshold = u, type = "GP",
time.units = "8629.913/year")
[1] "Normal Approx."
95% lower CI Estimate 95% upper CI
10-year return level 8.802749 9.423588 10.04443
50-year return level 9.625317 11.030762 12.43621
100-year return level 9.837487 11.718026 13.59857
明らかに結果が変わっていますね…。台風19号の影響はすさまじいということでしょうか…。
最後に
ということで、データ入手から、欠損値の補完、極値理論を用いた解析までを書き連ねました。今回思ったのが、極値解析をやるならRだなと思いました。ライブラリが充実していてちょっとした解析ならポンっとできてしまいます。
なお、断っておきたいのが、私は河川の専門家ではなく、単に極値理論を少し知っているということです(修士論文で研究した程度)。データ解析を行うには、扱うデータの裏側まで知り、それに応じた仮定を置いていく必要がありますが、そのあたりは何も考慮せずに、単に集めたデータを統計モデルに放り込んだという程度の解析になります。
ちなみに、多摩川の堤防についてはこんな記事を見かけました。
『暫定堤は14・5メートル前後の最低限のもので、過去の記録を踏まえると越水の恐れがあるため、国は16メートル前後の正規の堤防が必要と訴える』
今回対象にした田園調布(上)とは場所が違うのかもしれませんが、14.5メートルの堤防でも私のなんちゃって解析だと十分なのではと思ってしまいますが、やはり単に水位を基にした分析ではなく、色んな要素を加味しているんだろうなと感じた次第です。