当たり判定は標準でよく入っているので、アルゴリズムまで考えたことがない人もけっこう居ると思います。今回は、ちょっと粘って原理を考えてみます。
複雑・高速なものはもっとあると思いますが、これは一番シンプルなアルゴリズムかと思います。
今回は四角 x 四角なので矩形(読みは「くけい」)とも呼ばれると思います。
ここでは矩形を「四角」と呼びます。
当たり判定に必要な情報
最初に当たり判定に使う情報をリストアップします。
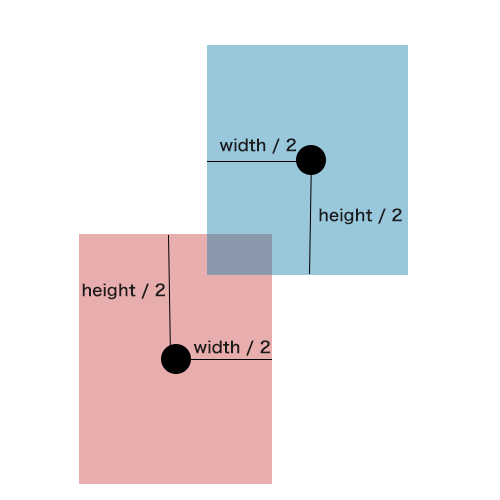
■ 中心の位置 (x,y)
■ 横幅 (width)
■ 高さ (height)
これが揃ってれば当たり判定ができるよ、という話です。
まだ何も話が進んでないのでとりあえず鵜呑みでいきましょう
「横の条件」と「縦の条件」がある
横について
1 . まず距離を出そう
位置をもとにして距離をだします。
距離 = (赤のX - 青のX)の絶対値
です。
なぜ絶対値なのかというと、マイナスにしたくないからです。
赤(3,10)、青(5,20)の場合は、2
赤(30,2)、青(18,2)の場合は、12
と、どんな場合でも同じように扱えます。
2 . ふたつの幅 ÷ 2 を 足す
それは、赤.width /2 + 青.width/2
で出せます。
3 . 1と2を比べる
さて、1と2を使うと衝突状態を検出できると思いませんか?
1 < 2の時です。
これは言葉で並べても腑に落ちないと思うので、イメージしてみてください。
1 < 2の時、衝突です。
縦について
横について「x」や「width」を扱っていたのを「y」や「height」に変えるだけです。
判定しよう
「縦について」「横について」両方衝突検出できていれば衝突です。
JavaScript & Canvasで表現するのに必要な知識
原理の話が終わったので、これからは表現していきます。
お気づきのように、絶対値を出す標準関数のMath.abs()が必要です。
var absNum = Math.abs(-10); // 10
それと、Canvasで四角を表現するならばrect()が必要です。
rect (x, y, width, height)で描画されます。
rect (100,100,10,10); //(100,100)に幅、高さ10の四角を描く
さあ、やってみましょう。
<script>
function setup(){
var canvas = document.getElementById('MyCanvas');
if (canvas.getContext){
ctx = canvas.getContext('2d');
//赤い四角
var red = {
x : 100,
y : 100,
width : 80,
height : 100
};
//青い四角
var blue = {
x : 160,
y : 180,
width : 100,
height : 130
};
// 当たり判定
if(
Math.abs(red.x - blue.x) < red.width/2 + blue.width/2 //横の判定
&&
Math.abs(red.y - blue.y) < red.height/2 + blue.height/2 //縦の判定
){
console.log("hit"); // hit
}
//rectの基準点は左上になっているので、描画時に基準点を真ん中にしてます。
ctx.rect(red.x - red.width/2,red.y - red.height/2,red.width,red.height);
ctx.rect(blue.x - blue.width/2,blue.y - blue.height/2,blue.width,blue.height);
ctx.fill();
}
}
</script><html><head><style type="text/css">canvas { background:#FAFAFA;}</style></head><body onload="setup();"><canvas id="MyCanvas" width="500" height="500"></canvas></body></html>
なぜ「差の絶対値」なのか?アゲイン
「差の絶対値」を出すことの恩恵は4つのパターンに対応できることですね。
下の4つのパターン全てできることをイメージしてみてみましょう。できそうですね。