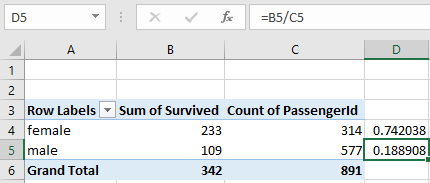はじめに
- データサイエンスに興味がある
-
Excelなら使える
- ピボットテーブルなら聞いたことあるぞ!
という方々向けに、Excelの基本的な機能と関数のみを使って、データ分析(重回帰分析)を行う流れを説明していきたいと思います。
みなさまが本格的なデータサイエンスの勉強を始める前の足掛かりとなれば幸いです![]()
分析
0. 目的
1912年の北大西洋にて、当時最大の旅客船である「タイタニック号」が沈没した事件はみなさまご存知でしょう。実は、乗客全員が死亡したわけではなく、何とか生存することができた人たちもいました。
それでは、どのような人たちが生き残ったのでしょうか?
- 階級の高い乗客が優先的に助けられたのでは?
- 体力がありそうなので若い男性が生き残ったのでは?
- ...
などなど、いろいろ考えられますよね。
今回は、このような仮説が本当か?ということをデータ分析で検証しながら、最終的に乗客の情報をインプットすると、その乗客が生存したか否かをアウトプットしてくれる関数を作成することを目指していきましょう。
1. 準備
以下の手順に従って**「タイタニック号の乗客データ」**をダウンロードしましょう。
- Kaggleに登録
- https://www.kaggle.com/
- 注:Kaggleとはデータサイエンティストが腕を競い合うSNSのようなものです
- タイタニック号の乗客データ(
train.csvとtest.csv)をダウンロード
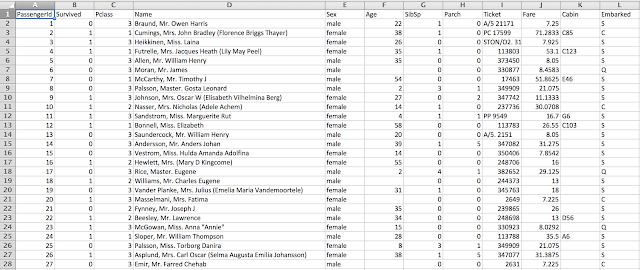
エクセルでtrain.csvを開くと、以下のようなデータが見れるはずです。
2. データを概観する
2-1. 変数の意味を調べる
まずは、それぞれの列(=変数)が何を意味しているのかを確認しましょう。
Kaggleに記載されているデータセットの情報を見ると、以下の説明があります。
- PassengerID
- 乗客の番号
- Survived
- 生存結果
- 1 = 生存
- 0 = 死亡
- 生存結果
- Pclass
- 乗客の階級
- 1 = 1st
- 2 = 2nd
- 3 = 3rd
- 乗客の階級
- Name
- 乗客の名前
- Sex
- 性別
- Age
- 年齢
- SibSp
- 兄弟、配偶者の数
- Parch
- 両親、子供の数
- Ticket
- チケット番号
- Fare
- 乗船料金
- Cabin
- 部屋番号
- Embarked
- 乗船した港
- C = シェルブール(フランス)
- Q = クイーンズタウン(ニュージーランド)
- S = サウサンプトン(イギリス)
- 乗船した港
年齢や性別だけでなく、兄弟の数や、乗船した港もわかるようですね。
果たしてこれらの情報は生存したかどうかに関係があるのでしょうか?
2-2. ピボットテーブルをつくる
それぞれの変数が生存したかどうかに関係があるかを確認するためには、ピボットテーブルを使います。以下のいずれかの方法でピボットテーブルを作ってみてください。できない場合はこちら
![]() ピボットテーブルの作り方
ピボットテーブルの作り方
- [挿入]から[ピボットテーブル]をクリックして、データの範囲を選択
- データの範囲全体を選択して、
Alt->N->VでもOK
- データの範囲全体を選択して、
2-2-1. 軸を決めて比較する
ピボットテーブルをつくると、特定の軸を決めて比較することができます。
たとえば、性別ごとや乗客の階級ごとの生存率を見ることができます。
ここは全くデタラメにやっても構いませんが、0. 目的でも言及したように「階級の高い乗客が助かったのでは?![]() 」「体力がありそうなので男性が生き残ったのでは?
」「体力がありそうなので男性が生き残ったのでは?![]() 」などと、仮説を持ちながら検証していくと質の高い分析になるでしょう。
」などと、仮説を持ちながら検証していくと質の高い分析になるでしょう。
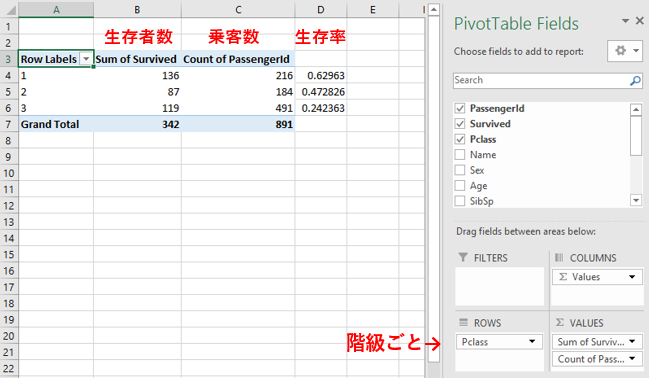
まずは、乗客の階級ごとの生存率を見てみましょう。
果たして階級が高い乗客の方が生存率が高いのでしょうか?
![]() ピボットテーブルで乗客の階級ごとの生存率を見る
ピボットテーブルで乗客の階級ごとの生存率を見る
- ROWS(行)に
Pclassを入れる - VALUES(値)に
Sum of Survived(=生存者数)とCount of PassengerId(=乗客数)を入れる - 生存率
= 生存者数/乗客数を計算する
一等級の生存率は63%ですが、二等級は47%、三等級は24%と下がっていっています。
これより階級の高い乗客は生存率が高いことがわかり、仮説は立証されました。
同様にして、性別ごとの生存率を見てみましょう。
果たして男性のほうが生存率が高いのでしょうか?
ROWS(行)にPclassではなくSexを入れるだけですね。
男性の生存率が19%で、女性の生存率が74%。
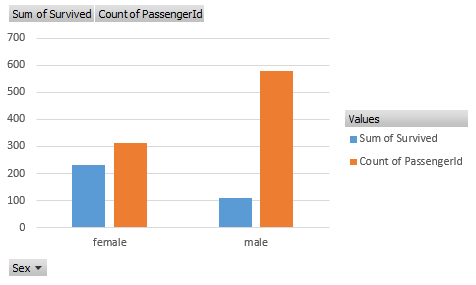
以下のようにグラフにしてみると差が一目瞭然です。
![]() ピボットテーブルからグラフをつくる
ピボットテーブルからグラフをつくる
- ピボットテーブルの適当な場所をクリックした状態で、[挿入]から[おすすめのグラフ]をクリック
- または
Alt->N->RでもOK
- または
つまり、女性の生存率が非常に高いことが分かり、仮説が棄却されました。
AgeやSibSp(兄弟、配偶者の数)、Parch(両親、子供の数)など他の変数とSurvivedの関係もぜひ手作業で確認してみてください◎
![]() コラム:なぜ女性の生存率が高いのか?
コラム:なぜ女性の生存率が高いのか?
実は、当時日本人としてただ一人の乗客であった細野正文氏によるタイタニック号事故生き残りの手記に、以下のような記述があります。
... 船客はさすがに一人として叫ぶ者はなく、皆落ち着いていたことは感心すべきことだと思った。ボートには婦人たちを優先的に乗せた。その数が多かったため、右舷のボート4隻は婦人だけで満員になった。その間、男子も乗ろうと焦る者も多数いたが、船員は拒んで短銃を向けた。この時船は45度に傾きつつあった。
乗客はパニック的状況の中でも焦らず、徹底して女性を優先的に救助していたようですね。
2-2-2. 欠損値をチェック
次に、「空欄になっていてデータが入っていないセル」に注目しましょう。
データ分析用語では、欠損値と呼びます。
パッと見ると、AgeやCabinのデータが歯抜けになっていますが、欠損値がどれくらいの割合を占めているかピボットテーブルを使って確認しておきましょう。
ピボットテーブルのROWS(行)にAgeを入れてみてください。
すると、空欄になっているデータが177個あることがわかりました。
全体のデータが891個なので、2割ほどのデータが欠損しているようです。
2-3. 相関係数を計算する
「2つの変数がどれくらい関係があるか」を-1から1で表した、相関係数と呼ばれる指標があります。
この指標が1に近いほど、「片方の変数が大きいとき、もう片方も大きくなる」傾向にあり、これを正の相関と呼びます。
逆に、-1に近いほど、「片方の変数が大きいとき、もう片方は小さくなる」傾向にあり、負の相関と呼びます。
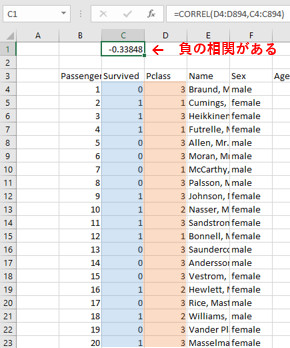
たとえば、2-2-1. 軸を決めて比較する で検証したように、「乗客の階級が1に近い(小さい)とき、生存率が高い(大きい)」ことがわかっていますので、乗客の階級と生存率は負の相関になっているはずです。確認してみましょう。
![]() 相関係数を計算する
相関係数を計算する
-
=CORREL(変数の範囲, 変数の範囲)で、Survivedのデータの範囲とPclassのデータの範囲を指定すればOK
3. データを整形する
ここからは本格的にモデルを組むため、データをモデルが読み込みやすい形に整形していきましょう。
3-1. 使わない変数を削除する
まずは、必要のない変数を削除します。
ここでは、分析のやりにくそうなTicketとNameを分析に使わないことにして、削除してしまいます。
逆に、2. データを概観する で検証したようにSexやPclassは生存率に大きくかかわる変数ですので、必ず残しましょう。
3-2. ダミー変数をつくる
さて、分析を行うために、SexやPclassなど、数字ではないデータをダミー変数に変換する必要があります。
ダミー変数とは、数字ではないデータを「0」か「1」で表すことです。
以下の要領で実際に変換してみましょう。
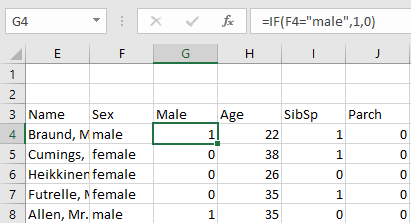
![]() Sexをダミー変数に変換する
Sexをダミー変数に変換する
- 男性であること1か0で表す変数
Maleの列を追加する =IF(参照セル="male", 1, 0)- すべての行が埋まるように縦にコピーする
このようにすると、変数Maleが1のとき男性、0のときは女性を意味します。
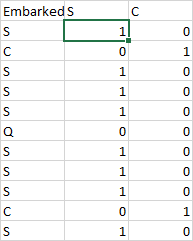
![]() Embarked(乗船した港)をダミー変数に変換する
Embarked(乗船した港)をダミー変数に変換する
- 乗船した港がサウサンプトンであること1か0で表す変数
Sの列を追加する =IF(参照セル="S", 1, 0)- すべての行が埋まるように縦にコピーする
- 同様に、乗船した港がシェルブールであることを1か0で表す変数
Cの列を追加する =IF(参照セル="C", 1, 0)- すべての行が埋まるように縦にコピー
![]() コラム:乗船した港がクイーンズランドであることを示す変数は要らないの?
コラム:乗船した港がクイーンズランドであることを示す変数は要らないの?
もちろん作ることができます。=IF(参照セル="Q", 1, 0)とすればいいですね。
しかしながら、SとCがともに0のとき、それはQになりますよね?
Sexの変数に対して、変数Maleしか作らなかったのと同様にして、あえて作っていません。
次に、Cabin(部屋番号)のデータもダミー変数にしていきます。
部屋番号の種類は膨大な数があるため、各部屋番号に対してひとつひとつダミー変数を作っていくと埒があきません・・・。
"Titanic Cabin"でGoogle 画像検索をかけてみると以下のような画像が出てきます。

客室の階数によってAからGまでラベルが降られているようですね!
Aに近ければ近いほど、救命ボートに近いため生存確率が上がりそうだな、などということを考えつつ、部屋番号の頭に付いている英字がCのとき、Eのとき、Gのとき、とダミー変数を作っていくことにします。
![]() Cabinをダミー変数に変換する
Cabinをダミー変数に変換する
- Cabinの頭の英字がCであること1か0で表す変数
CabinCの列を追加する =COUNTIF(参照セル, "C"&"*")- 同様の作業をA~Fで行う
-
*(アスタリスク)はワイルドカードと呼ばれ、「どんな文字でもいいですよ」という意味 - ふつうの
=IF()ではワイルドカードは使えないので=COUNTIF()を使う
3-3. データを補完する
最後に、2-2-2.で見た欠損値を何とかして補完していきます。
以下のような方法が考えられます。
統計量を使って補完
-
Ageの欠損値を「平均値」や「中央値」で代替
他の変数のデータを使って補完
- たとえば、
CabinとPclassの相関をチェック- もし相関があれば、Pclassが1に近い人はCabinもAに近いようにする
今回は簡単のため、Ageの欠損値を平均値=AVERAGE()で埋めて、Cabinの欠損値はそのままにしておきましょう。
4. モデルをつくる
4-1. 重回帰分析を行う
重回帰分析とは、乗客にかんする情報が、乗客の生存可能性にどれくらい寄与しているかを分析する手法のひとつです。このとき、乗客にかんする情報のことを説明変数と呼び、乗客の可能性のことを目的変数と呼びます。
式に表すと、以下のような形になります。(回帰式)
$y = a_1x_1 + a_2x_2 + ... + a_nx_n + b$
たとえば... アイスクリームの売り上げ数 = 30 * 気温 + -5 * 値段 + 100
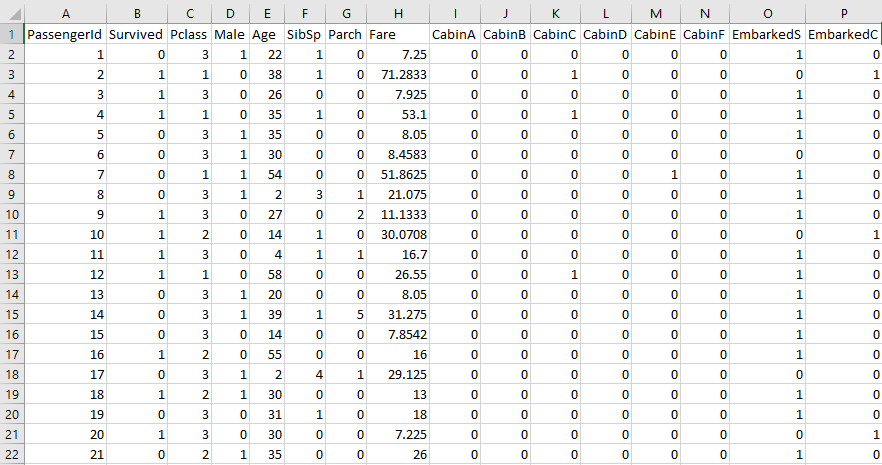
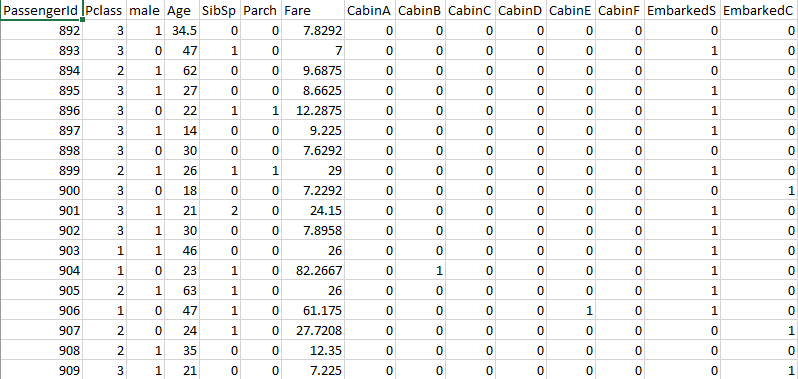
もし無事にデータ整形が完了していれば、データは以下のように数字だけになっているはずですので、これに対して重回帰分析を行っていきましょう。
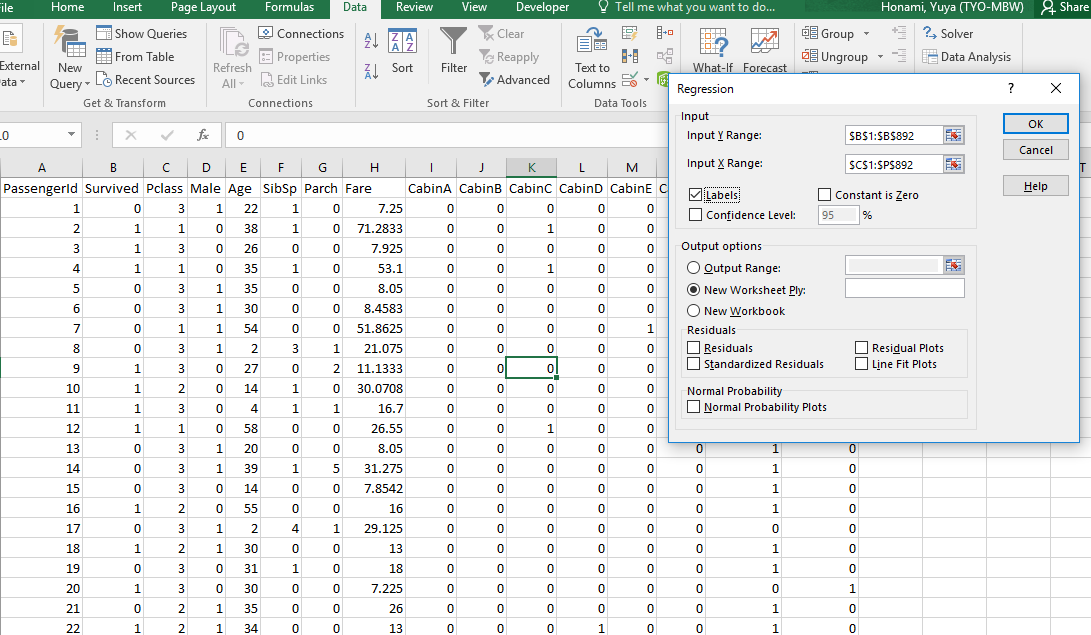
![]() 重回帰分析を行う
重回帰分析を行う
- [ファイル] タブをクリックし、[オプション] をクリックして、[アドイン] カテゴリをクリック
- [管理] ボックスの一覧の [Excel アドイン] をクリックし、[設定] をクリックします
- [アドイン] ボックスで、[分析ツール] チェック ボックスをオンにし、[OK] をクリック
- シートに戻り、[データ]→[データ分析]→[重回帰分析]とクリック
- [入力Y範囲]にSurvivedの列の範囲を選択(目的変数)
- [入力X範囲]にそれ以外の変数の範囲を選択(説明変数)
- [ラベル]にチェックを入れておく
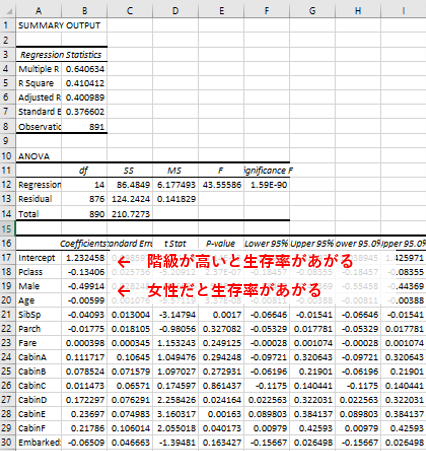
うまくいけば、以下のように重回帰分析の結果が得られるはずです。
Coefficients(係数)の部分に書かれている数字が、
以下の式でいうところの$a_1, a_2, ... , a_n, b$に相当しています。
$y = a_1x_1 + a_2x_2 + ... + a_nx_n + b$
すなわち、回帰式の係数が分かったので、乗客の情報(つまり$x_1, x_2, ..., x_n$)を入れれば生存するかどうかがわかるモデルが完成しました!
4-2. 推定する
さて、得られたモデルを使って、乗客の情報から生存予測をしてみましょう。
まずは、test.csvからテストデータを開き、分析に使ったデータと同じ形式に変換してください。
Regression, Survivedという2つの列を追加したのち、以下の手順で推定を行っていきます。
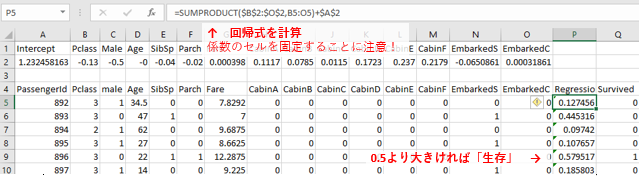
![]() 作ったモデルを使って生存予測をする
作ったモデルを使って生存予測をする
- 回帰式の係数をコピーし、適当な場所に
Ctrl + Alt + Vで縦横を転置して貼り付け -
SUMPRODUCT(ベクトル, ベクトル)を使って回帰式を計算 - 閾値を設定して
=IF(得られた値 > 閾値, 1, 0)を使って1か0に変換する
![]() コラム:閾値はどういう意味?
コラム:閾値はどういう意味?
重回帰分析は、アイスクリームの売り上げなどのようにあくまでも「実数」を返すモデルです。
しかし、今回は生存したかしていないかを「生存」か「死亡」で表現しなければいけないため、
- モデルがはじき出した数字が1に近ければ「生存」つまり1
- 0に近ければ「死亡」つまり0
という形で変換を施しています。
4-3. 検証する
最後に、モデルで得られた生存予測を検証してみます。
まずは、テストデータと予測結果いをPassengerID, Survivedだけ残してcsvで出力してください。
それをSubmit FormからKaggleに提出すればOKです
結果を見ると、Excelで作ったモデルは**正答率76%**を記録しました![]()
あとがき
いかがでしたでしょうか?
Excelの関数・機能のみを使ってデータ分析を行うイメージが付きましたでしょうか![]()
Excelは、
- そんなに重くないデータを概観するにはとてもよい
- ピボットテーブルやグラフなども使いやすい
- 重回帰分析もワンクリックでできる
- 実はすべての変数の相関係数を一気に見ることもできる
- データ分析の機能をオンにして、「相関」を使えばOK
などなど、データサイエンスをはじめるに当たって基礎的な機能はしっかり持っていますので、
特に初めたてのころは、Excelだけを使ってある程度の分析を行っていけるかと思います![]()
なお、これ以上の分析をやりたい方々は、ぜひPythonやRを使っていきましょう。
- Excelの重回帰分析には16変数までという制限がある
- PythonやRを使えばダミー変数化も一発だし、さまざまなモデルがさまざまなライブラリから提供されている
など、Excelだけでは手の届かない分析に簡単に手を伸ばすことができます。
インターフェイスが変わるので取っ付き辛いですが、上記で学んだ基本的な考え方を応用しながら、ぜひトライしてみてください![]()
https://qiita.com/hik0107/items/19dd2f6a4ab61ec21905
https://qiita.com/hik0107/items/ef5e044d2f47940ba712
https://qiita.com/hik0107/items/3dc541158fceb3156ee0