【PythonとStanで重回帰】「StanとRでベイズ統計モデリング」の5.1節をやってみた（PyStan）

#書籍「StanとRでベイズ統計モデリング」

第4節に続き実践して参ります。
Python（PyStan）で「StanとRでベイズ統計モデリング」の4節をやってみた

「StanとRでベイズ統計モデリング」のRコードをPythonに書き換え、PyStanを使えるようになるのが主な目的です。なので重回帰やStanモデルの説明は書籍にお任せで、ここでは解説していないのでご注意ください。

尚、5.1節は著者様がブログで直接やってくれているので、この記事はそのグレードダウン（初学者が泥臭くやってる）版ですｗ
→Python（PyStan）で「StanとRでベイズ統計モデリング」の5.1節を実行する

##環境

Ubuntu16.04(Windows10 Bash on Windows)
Python3.6.3(Anaconda5.0.1)

※Windowsだとコンパイル無限地獄に陥る可能性があるとのことでBoWに避難。回避方法は上記記事にて著者様が書いてくれている。
コンパイル無限地獄の回避方法※Windows

##前準備

###Github（本記事で使用してるデータセットとモデル）
https://github.com/MatsuuraKentaro/RStanBook/tree/master/chap05

内容は学生の出席率に関する架空データ50人分です。
解析の目的は、与えられた二つの説明変数を使って、応答変数を精度よく予測することです。

PyStanのインストールについては上記の著者ブログ記事を参照頂くのが良いですね。

※こうするとわかりやすい見やすいってかそもそも間違ってるなどご指摘があったらコメント頂けると幸いです。

##P54 5.1 重回帰

それでは早速実践です。Pythonコードを載せつつ説明していきます。

python

# P54 Chapter5.1

import os
import math
import pickle
import pystan
from pystan import StanModel
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats
import functools
from hashlib import md5
import pickle
%matplotlib inline

# StanModelをいちいちコンパイルし直すのは面倒なので、こちらの関数で保存しロードする
def StanModel_cache(model_code, model_name=None, **kwargs):
    """Use just as you would `stan`"""
    # 公式の'ascii'ではうまくいかないので、'utf-8'に変更
    code_hash = md5(model_code.encode('utf-8')).hexdigest()
    if model_name is None:
        cache_fn = 'stan_pkl/cached-model-{}.pkl'.format(code_hash)
    else:
        cache_fn = 'stan_pkl/cached-{}-{}.pkl'.format(model_name, code_hash)

    try:
        sm = pickle.load(open(cache_fn, 'rb'))
    except: #tryで例外が発生すれば、smを書き込み
        sm = StanModel(file=model_code)
        with open(cache_fn, 'wb') as f:
            pickle.dump(sm, f)
    else: # tryで例外が発生しなければ、"Using cached StanModel"をプリント
        print("Using cached StanModel")
    return sm


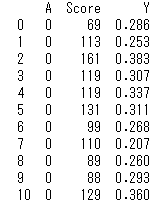
data = pd.read_csv('RStanBook/chap05/input/data-attendance-1.txt') # データセットを読み込む
data = data.sort_values(by = 'A').reset_index().drop('index', axis=1) # Aでソート

print(data)

#stan_dataの作成→辞書
stan_data = data.copy()
N = len(stan_data)
stan_data.Score /= 200 # スケーリングして絶対値を揃える
stan_data = stan_data.to_dict('list')
stan_data.update({'N':N})

# とりあえずデータを見てみる
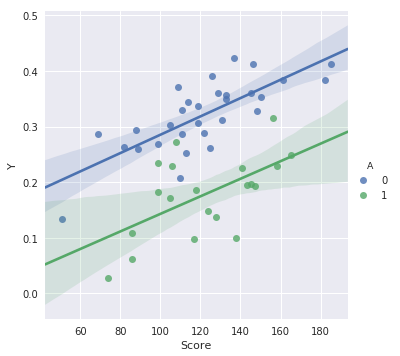
sns.lmplot(x='Score', y='Y', hue='A', data=data)

※StanModel_cache()関数は、StanModelのコンパイルをPython起動の度にせずとも、コンパイル済みのデータを保存してロードできるようにしたものです。これはなくても問題ないので詳細は割愛します

とりあえずデータの概要を眺めるべく一部を出力しました。
散布図ととりあえずの回帰直線を見ると、相関はありそうな様子が見て取れますね。

書籍ではP56でデータの分布を確認するために散布図行列をRで出力しています。しかし！Pythonでこれと同様のものをサクッと出力する方法を私は知りません。泥臭く1個1個作ることはできそうですが、これは描画を頑張る記事ではないので、簡単化しておきますｗ

python

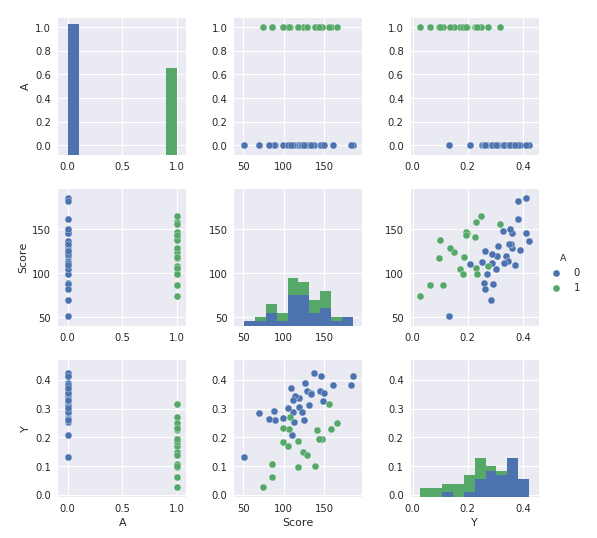
sns.set(font_scale=1)
sns.pairplot(data, hue="A", size=2.5, diag_kind='hist')

図5.1

pairplotで一部を箱ひげにしたりspearmanの相関係数を出す方法はなさそうなので、本気でやるならPairGridで頑張るしかないのかな。

###P58 StanModelのコンパイルとMCMCサンプリング

データの概要を一通り眺めたところで、StanModelのコンパイルと事後分布のサンプリングをしていきましょう。
Stanコードや重回帰でのモデリング解説は書籍参照にて。

python

# コンパイル＆&保存（StanModel関数を直実行でもよし）
StanModel_cache(model_code='RStanBook/chap05/model/model5-3.stan')

# 保存したコンパイル済みのモデルを取り出す
with open('stan_pkl/cached-model-ccb3e87a1dc34687fa0d76c8a1bdd683.pkl', 'rb') as f:
    model = pickle.load(f) 

# MCMCサンプリング NUTS   
fit_nuts = model.sampling(data = stan_data, seed=1234, warmup=1000, chains=4)

# サンプリング結果を保存（なくても大丈夫）
with open('stan_pkl/fit5-3_20171130.pkl', 'wb') as f:
    pickle.dump(fit_nuts, f)

#MCMCサンプリング結果の抽出（トレースプロットを見るので全て抽出）
ms = fit_nuts.extract(permuted=False, inc_warmup=True)

#ウォームアップ（バーンイン）のサイズを取得
iter_from = fit_nuts.sim['warmup']

#ウォームアップを省いた区間の配列
iter_range = np.arange(iter_from, ms.shape[0])

#トレースプット描画の時はこちらを使う
iter_start = np.arange(0, ms.shape[0])

#各変数名を取得
paraname = fit_nuts.sim['fnames_oi']

実際の統計モデリングでは、ここに辿りつくまでが大変ですが、例題に甘えてサクサク進めていきます。
それではMCMCサンプリング結果を見てみましょう。

python

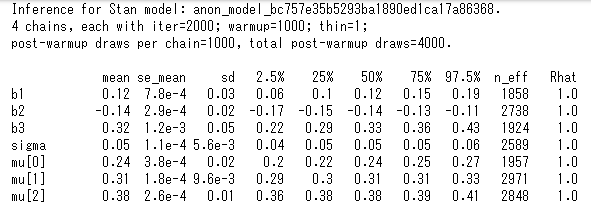
print(fit_nuts)

収束については3chain以上での実行で、各パラメータのRhatが1.1未満になっているか（収束しているか）をチェックします。問題はなさそうですね。

ちなみにfit_nuts.extract()は辞書と同じように値を取り出せるクラス型になっているので、各パラメータのサンプリングをfit_nuts.extract()['sigma']の様に直接取り出すこともできます。この場合はwarmupを除いた1000サンプリング×4chain=4000個の要素を持ったsigmaの配列を取り出せます。サンプリング後の各パラメータの平均を取り出したいときはfit_nuts.get_posterior_mean()で取り出すこともできますので、stanfitオブジェクトから何が取り出せるか見ておくのが良いですね。

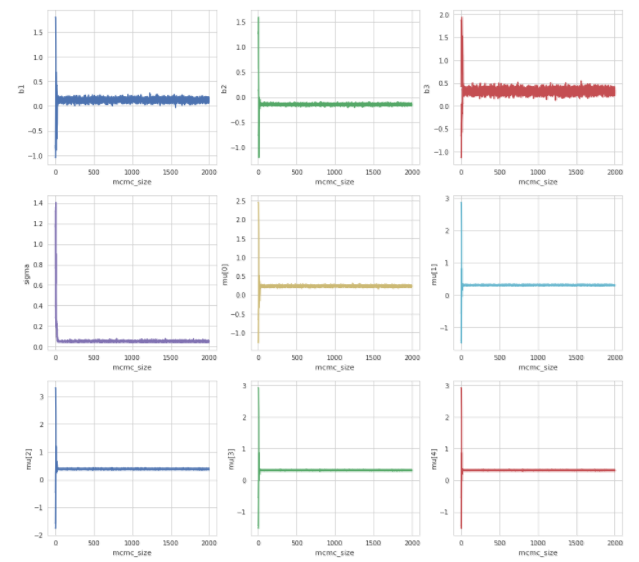
それではトレースプロットを見てみましょう。（パラメータ収束の様子）

python

# MCMCサンプリングの描画
# seabornおまじない
palette = sns.color_palette()
sns.set(font_scale=1)
sns.set_style('ticks')
sns.despine(offset=10, trim=True)

fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(16,15))

for i in range(3):
    for j in range(3):
        # カラーパレット使いまわし用
        if i>1: l=6
        else: l=0
        
        axes[i,j].plot(iter_start, ms[iter_start, :, i*3+j],
                      linewidth=2, color=palette[i*3+j-l])
        axes[i,j].set_xlabel('mcmc_size')
        axes[i,j].set_ylabel(paraname[i*3+j])
        axes[i,j].grid(True)

        fig.show()

どれも綺麗に収束していますね。

###P60 図によるモデルのチェック

統計モデリングの勉強してて思うのは、描画が大変だということｗ
統計の勉強をしていたはずが、気づいたら描画に四苦八苦して一日終了ということが少なからずある。。

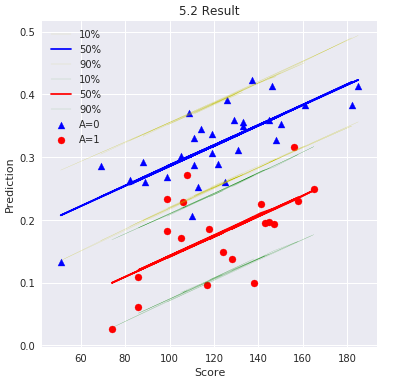
ここでは書籍に倣ってMCMCサンプリングの80%ベイズ予測区間を描画します。

python

quantile = [10, 50, 90] # 分位点（中央値と80%区間）
colname = [str(i) + '%' for i in quantile]

# stanモデル内で計算した事後分布から、回帰結果の各分位点を取得
for i in range(54, 104, 1):
    if i==54 :
        pred = np.percentile(ms[iter_range, :, i], q = quantile)
    else:  
        tmp_pred = np.percentile(ms[iter_range, :, i], q = quantile)
        pred = np.append(pred, tmp_pred)

pred = pd.DataFrame(pred.reshape(50, 3), columns=colname)

# 予測値の描画
sns.set_style("whitegrid")
sns.set(font_scale=1)
plt.title('5.2 Result')

# A=0
plt.plot(data['Score'][data.A==0], pred['10%'][:30], c='y', lw=0.1)
plt.plot(data['Score'][data.A==0], pred['50%'][:30], c='b') 
plt.plot(data['Score'][data.A==0], pred['90%'][:30], c='y', lw=0.1) 
plt.scatter(data['Score'][data.A==0], data['Y'][data.A==0], c='b', marker='^', label='A=0')

# A=1
plt.plot(data['Score'][data.A==1], pred['10%'][30:50], c='g', lw=0.1)
plt.plot(data['Score'][data.A==1], pred['50%'][30:50], c='r') 
plt.plot(data['Score'][data.A==1], pred['90%'][30:50], c='g', lw=0.1) 
plt.scatter(data['Score'][data.A==1], data['Y'][data.A==1], c='r', marker='o', label='A=1')
plt.legend() # ラベルを表示
plt.xlabel('Score')
plt.ylabel('Prediction')
plt.show()

図5.2

実際はRで予測区間をグレーアウトしていますが、Pythonで同じ様にやる方法が見つからないので、黄色と緑の線で予測区間を囲っていますｗ
一部外れ値が見えますが、概ね予測区間に収まっていますね。

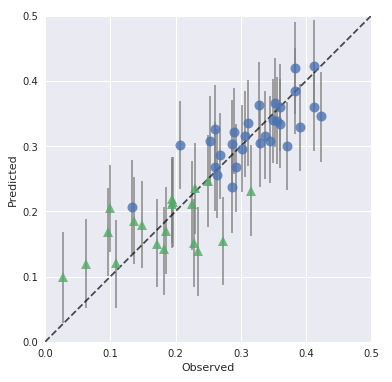
###P62 実測値と予測値のプロット

お次は実測値と予測値のプロットをしていくのですが、書籍では予測分布の中央値を〇、予測区間を線でプロットしています。ここでも描画コピーが危ぶまれたので、ここは著者様のブログのコードを拝借させて頂きましたｗ

Python（PyStan）で「StanとRでベイズ統計モデリング」の5.1節を実行する

python

# warmupを含まない通常のサンプリングデータ抽出
ms_n = fit_nuts.extract()
quantile = [10, 50, 90]
colname = ['p' + str(x) for x in quantile]

# percentileの行方向指定で、各学生の10%、50%, 90%の値を取得。それを行ベクトルから列ベクトルに変換
df_qua = pd.DataFrame(np.percentile(ms_n['y_pred'], q = quantile, axis=0).T, columns=colname)
d = pd.concat([data, df_qua], axis=1)
d0 = d[d.A == 0]
d1 = d[d.A == 1]

palette = sns.color_palette()
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot([0, 0.5], [0, 0.5], 'k--', alpha=0.7)
ax.errorbar(d0.Y, d0.p50, yerr=[d0.p50 - d0.p10, d0.p90 - d0.p50],
           fmt='o', ecolor='gray', ms=10, mfc=palette[0], alpha=0.8, marker='o')
ax.errorbar(d1.Y, d1.p50, yerr=[d1.p50 - d1.p10, d1.p90 - d1.p50],
           fmt='o', ecolor='gray', ms=10, mfc=palette[1], alpha=0.8, marker='^')
ax.set_aspect('equal')
ax.set_xlim(0, 0.5)
ax.set_ylim(0, 0.5)
ax.set_xlabel('Observed')
ax.set_ylabel('Predicted')

図5.3

matplotlibにはerrorbarなんてものも用意されてるんですね。勉強になります。

上記の図で、予測値と実測値が完全に一致している場合は黒の点線で引いてある対角線上にプロットされます。ここでも一部予測区間からの外れ値が見えますが、概ね区間に収まっていることがわかるので、モデル自体は悪くなさそうです。

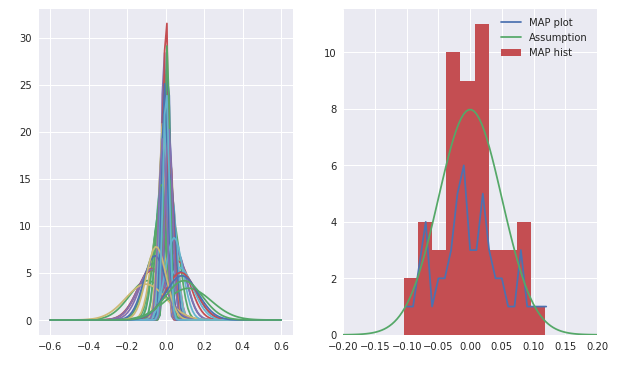
続いて推定された誤差分布が、仮定していた$N(0, σ)$にあてハマっているかどうかを確認します。

python

e_list = []
mu_list = []
sd_list = []

# 学生毎のMCMCサンプリング結果分布
for i in range(4, 54, 1):
    error = data['Y'][i-4] - ms[iter_range, 0, i]
    e_list.append(error)
    
for i in range(len(e_list)):
    
    mu_list.append(e_list[i].mean())
    sd_list.append(np.sqrt((e_list[i]**2).sum()/(len(e_list[i])-1)))
  

plt.figure(figsize = (10,6))
sns.set(font_scale=1)
plt.subplot(1,2,1)

x = np.linspace(-0.6, 0.6, 100)
for i in range(len(mu_list)):
    nor = stats.norm.pdf(x, loc=mu_list[i], scale = sd_list[i])
    plt.plot(x, nor)

# 各学生の評価の正規分布から代表値を取り出しプロットする
# 代表値はMAP推定値＝事後確率最大値とするので、平均μとする（正規分布だし）
# 50個のMAP推定値をプロットする上で、そのままプロットすると全て違う値になってしまうので、第3位以下を四捨五入してプロットする
unq, cnt = np.unique(np.round(mu_list,2), return_counts=True)
df = pd.DataFrame({'er':unq, 'count':cnt})
x = np.linspace(-0.2, 0.2, 100)
nor_a = stats.norm.pdf(x, loc=0, scale=0.05) # σはMCMCサンプリングから得られた平均をそのまま

plt.subplot(1,2,2)
plt.plot(df['er'], df['count'])
plt.plot(x, nor_a)
plt.hist(mu_list)
plt.xlim(-0.2, 0.2)
plt.show()

図5.4

これが書籍に載っている図と微妙に違うんですよね。。カスりぐらいはしてる気がするのですが、何が違うのだろうか。これが心残りです。
ただ、仮定していた誤差分布と推定によって導かれた誤差の分布は概ねマッチしていそうなので良かったです。

尚、右図の折れ線はMAP推定値をプロットしていますが、MAP推定値＝最頻値ってことで、予測値を小数点第三位で四捨五入した値をカウントして求めたんですがそれは大丈夫なのだろうか。でも四捨五入しないと全部違う値だから1直線になるし。。
ここは良い方法がわかったら修正したい。
MAP推定が何かよく分からない方はご参考までに
→【Pythonで統計入門】最尤推定/MAP推定をPythonでやってみた

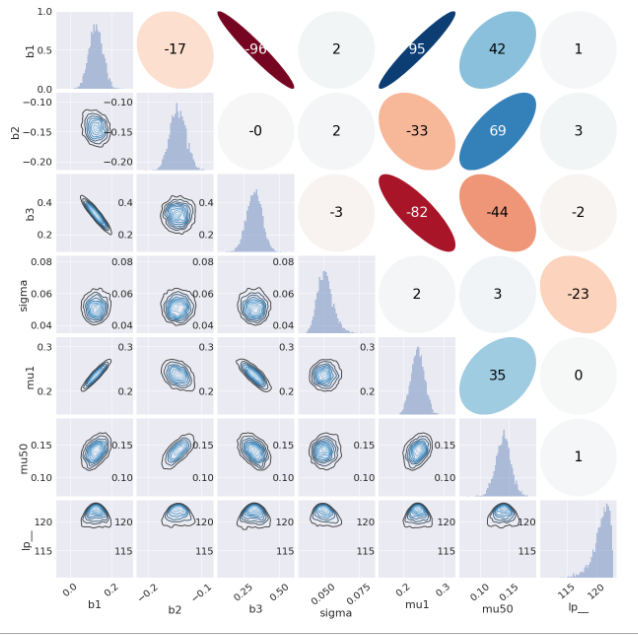
それでは最後にMCMCサンプルの散布図行列を載せて終わり。
冒頭と同様、これは完全にお手上げ状態だったので、著者様のブログ（前出のリンク）からコードを拝借させて頂きました。。ｗ

python

import math
from matplotlib.patches import Ellipse

ms_s = fit_nuts.extract()

def corrfunc(x, y, **kws):
    r, _ = stats.spearmanr(x, y)
    ax = plt.gca()
    ax.axis('off')
    ellcolor = plt.cm.RdBu(0.5*(r+1))
    txtcolor = 'black' if math.fabs(r) < 0.5 else 'white'
    ax.add_artist(Ellipse(xy=[.5, .5], width=math.sqrt(1+r), height=math.sqrt(1-r), 
                          angle=45, facecolor=ellcolor, edgecolor='none', transform=ax.transAxes))
    ax.text(.5, .5, '{:.0f}'.format(r*100), color=txtcolor, fontsize=28,
           horizontalalignment='center', verticalalignment='center', transform=ax.transAxes)
  
df = pd.DataFrame({'b1':ms_s['b1'], 'b2':ms_s['b2'], 'b3':ms_s['b3'], 'sigma':ms_s['sigma'],
                   'mu1':ms_s['mu'][:,0], 'mu50':ms_s['mu'][:,49], 'lp__':ms_s['lp__']},
                  columns=['b1', 'b2', 'b3', 'sigma', 'mu1', 'mu50', 'lp__'])
sns.set(font_scale=2)
g = sns.PairGrid(df)
g = g.map_lower(sns.kdeplot, cmap='Blues_d')
g = g.map_diag(sns.distplot, kde=False)
g = g.map_upper(corrfunc)
g.fig.subplots_adjust(wspace=0.05, hspace=0.05)

for ax in g.axes.flatten():
    for t in ax.get_xticklabels():
        _ = t.set(rotation=40)

この描画は大変勉強になるので、何度も見返して自分でもすぐ出せるようにしたいですね。

これにて5.1節のpystanを使った重回帰モデルは終了です。

次回は二項ロジスティック回帰だー。