Pythonで「StanとRでベイズ統計モデリング」の4節をやってみた（PyStan）

#書籍「StanとRでベイズ統計モデリング」

こちらの本、Stanで統計モデリングを始めるなら最高の内容になのですが、コードは全てR。
できたらPythonでやりたい！という方は多いと思います。ただPyStanの日本語記事って結構少ないので、RStanの内容をPyStanに置き換えたものを載せてみました。参考になればこれ幸い。

※Stanは勉強中、描画の知識も足りてないのでところどころ手抜き感あるかも。こうするとわかりやすい見やすいというのがあったらご指摘頂けると幸いです

##環境

Ubuntu16.04(Windows10 Bash on Windows)
Python3.6.3(Anaconda5.0.1)

※Windowsだとコンパイル無限地獄に陥る可能性があるとのことでBoWに避難した。回避方法もあるがLinuxの方が楽そう。Windowsの場合の注意点は一つなので、Windowsでもできます。（下記の中に注意点は記載）

セットアップはググれば綺麗なまとめがあるので割愛。

##前準備

###Github（本記事で使用してるデータセットとモデル）
https://github.com/MatsuuraKentaro/RStanBook/

##P34の4.4 単回帰から

ライブラリとデータ読み込み

python

import pystan
from pystan import StanModel
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline

data = pd.read_csv('RStanBook/chap04/input/data-salary.txt')

年収（Y）と年齢（X）の分布データ。

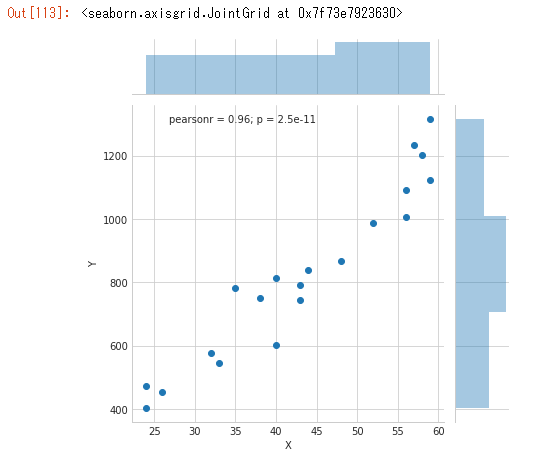
###データを描画

データの全体像、イメージを見ておく。

python

sns.set_style("whitegrid")
sns.jointplot(x="X", y="Y", data=data)

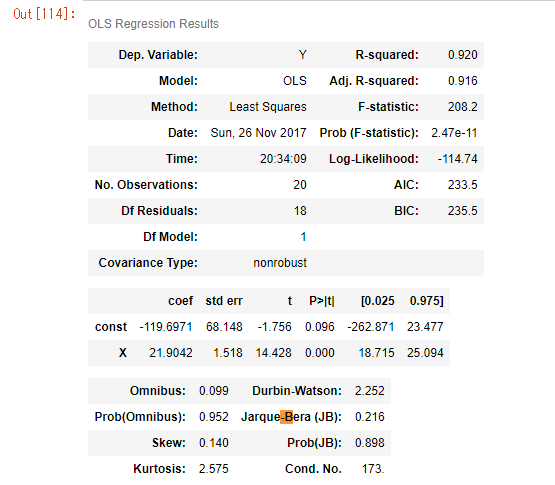
###単回帰分析をしてみる(statsmodels)

いきなりStanにぶち込むのも芸がないので、シンプルなものも見ておく。年収を年齢で回帰する。

python

import statsmodels.api as sm

y = data['Y']
x_c = sm.add_constant(data['X'])
mod = sm.OLS(y, x_c)
res = mod.fit()
res.summary()

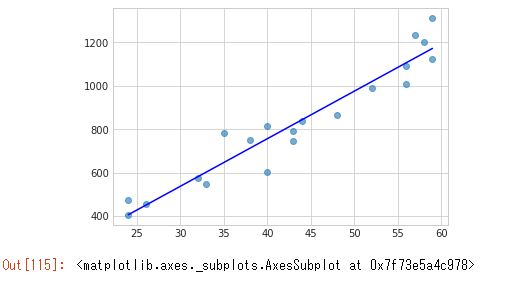
####単回帰の結果をプロット

python

plt.scatter(x, y, alpha=0.6)
plt.plot(x, res.fittedvalues, 'b-', label='OLS')
plt.show()

書籍の方でも超入門の例なので、これだけでかなり説明できているｗ

##PyStan

お待ちかねのPyStan

おおまかな流れとしては

1. モデルをコンパイル（ここでは既にGithubにあるmodelを使うので作成は省く）
2. MCMCを実行できるデータにする（データフレームから辞書型へ）。データサイズもデータセットに追加する
3. MCMCサンプリング。compileしたモデル.sampling(data=データセット)で実行。ここではNUTSを使用
   4.サンプリング結果を表示

python

#compile
model = StanModel(file='RStanBook/chap04/model/model4-5.stan')

#MCMC用のデータを作成
stan_data = data.to_dict('list')
stan_data.update({'N':len(data)})

#MCMCサンプリングの実行と結果を表示
fit_nuts = model.sampling(data = stan_data)
fit_nuts

※Windowsの人はここで注意
ここではNUTSというアルゴリズムでサンプリングを実行しているのだが、デフォルトだとコア数の分だけ並列で処理が行われる。しかし、Windowsの場合はそれだと無限コンパイル地獄に落ちる不具合があるので、model.sampling(data = stan_data, n_jobs=1)として並列を止める必要がある。詳しくはこちら。

####簡単な用語説明
mean
MCMCサンプルの平均値。事後平均。
se_mean
meanの標準誤差。MCMCサンプルの分散をn_effで割ったもの
sd
MCMCサンプルの標準偏差
2.5%, 97.5%
95%ベイズ信頼区間
25~75%
第１四分位～第３四分位
n_eff
Stanが判断したMCMCサンプル数（少なくとも１００は欲しい）
Rhat
MCMCが収束したかどうか。全てのパラメータで1.1未満であれば収束したとみなす（chain数も3以上など判断基準あり）

####個別にMCMCサンプリングの値指定もできる

python

fit_nuts = model.sampling(data = stan_data, pars=['b', 'sigma'], chains=3, 
                               iter=1000, warmup=200, thin=2, seed=123,
                               init='random')

data
データセット
pars
サンプリングの結果を保存するパラメータ（上記では1つ省いて試しに2つ保存してる）
seed
乱数の種（試行錯誤する場合は固定したほうがよい）
chains
chain数
iter
サンプリング数（試行錯誤段階では1000前後。最終確認では1000～5000くらいが良いらしい。中心極限定理の100倍の数で精度が上がる？）
warmup
初期値に影響されて最初は収束しない助走区間。200くらい。
thin
間引き数（MCMCサンプリングされる中で、全ての値をとっていくかいくつかのうちの1つをとっていくか）

※initの指定方法が分からなかったのでそのうち調べる

ちゃんと指定した値に変わっている。

MCMCサンプリング結果.simでMCMCサンプリングの中身を見れる。
また、辞書型でデータが格納されているのでkey指定で当然各パラメータの取得も可能。

python

print(fit_nuts.sim)

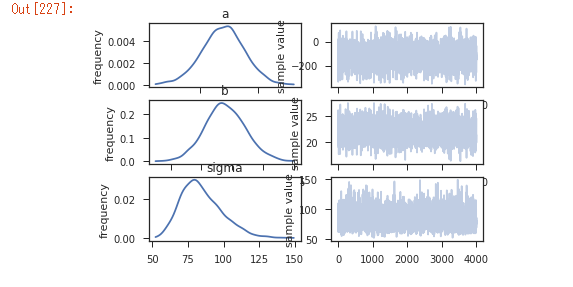
####MCMCサンプリング収束の様子を描画（トレースプロット）

下記の形で簡単にサンプリングの結果を描画できるが、、、

python

fit_nuts.plot()

↑ちょっとしょぼい。(´･ω･`)
色や値、サイズの指定ができない（少なくとも自分は知らない）ので、matplotlib, seabornで描画する。

サンプリング結果.extractでMCMCサンプリングの結果を取り出し、それをプロットしていく。

python

#MCMCサンプリングの結果を抽出
ms = fit_nuts.extract(permuted=False, inc_warmup=True)
#ウォームアップ（バーンイン）のサイズを取得
iter_from = fit_nuts.sim['warmup']
#ウォームアップの区間を省く
iter_range = np.arange(iter_from, ms.shape[0])
#各変数名を取得
paraname = fit_nuts.sim['fnames_oi']

#※※※今回は全て描画したいので、こちらを使う
iter_start = np.arange(0, ms.shape[0])

fit_nuts.extract(permuted=False, inc_warmup=True)について少し。
extractはMCMCサンプルを取り出す関数だが、デフォルトでは各chainもiterationの順番も混ぜて出力される。しかし、トレースプロットを描画するにはchainごとにiterationの順番を保持したままのMCMCサンプルが欲しいので、permuted=Falseと指定している。inc_warmup=Trueは、デフォルトで除外されるウォームアップを残すようにしている。

残りは取り出したトレースプロットの描画部分。
今回は切片と年齢の傾き、誤差項、事後確率の対数がパラメータとしてあるので、4次元のデータになっている。

python

#seabornのcolorpalette
palette = sns.color_palette()
#おまじない？
sns.set(font_scale=1)
sns.set_style("ticks")
sns.despine(offset=10, trim=True)

#複数グラフの描画（これしか方法知らない）
fig,axes  = plt.subplots(nrows=2, ncols=2, figsize=(15,10))

for i in range(2):
    for j in range(2):
        axes[i,j].plot(iter_start, ms[iter_start, :, i*2+j], 
                       linewidth=2, color=palette[i*2+j])
        axes[i,j].set_title(paraname[i*2+j])
        axes[i,j].set_xlabel('mcmc_size')
        axes[i,j].set_ylabel('parameter')
        axes[i,j].grid(True)

fig.show()

各パラメータが収束している様子が見える。

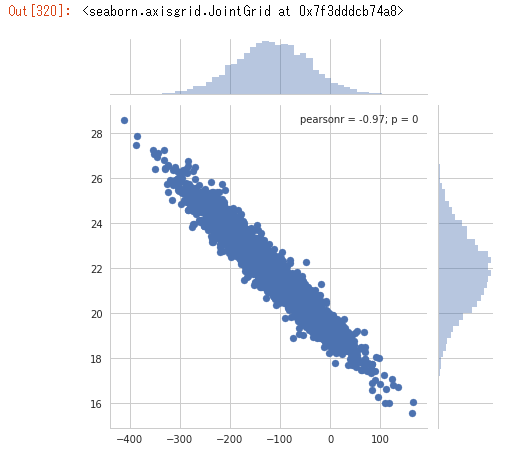
####パラメータの相関

続いてMCMCサンプリングから切片aと傾きbの相関を見てみる

python

sns.set_style("whitegrid")
g = sns.jointplot(x=ms[iter_range,:,0], y=ms[iter_range,:,1])
g.set_axis_labels("a", "b")

綺麗な負の相関。当然と言えば当然。固定された観測データに合わせて切片と傾きを調整しているので、両方の値が増加していったらどんどんデータから離れていってしまうｗ

####観測データと予測データを描画

観測データとMCMCサンプルから年収へ回帰したデータをプロットしてみる。

python

# mcmcサンプルからの抽出する数
sample = 10
# 乱数でプロットする値を抽出（ウォームアップは除く）
plot_range = np.random.randint(iter_from, ms.shape[0], sample)
# 観測データに観測データであることを示すカラムを追加
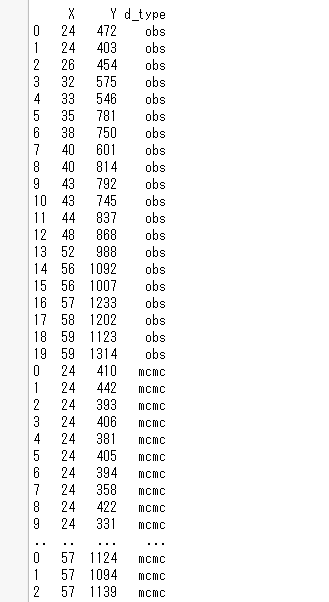
obs = pd.DataFrame({'X':data['X'], 'Y':data['Y'], 'd_type':'obs'})

# 年齢毎の年収をMCMCサンプルの結果に従い取得
for i in range(24, 60, 1):

    # 年収を年齢で回帰
    y_salary = pd.Series(np.array(ms[plot_range, 0, 0]) + np.array(ms[plot_range, 0, 1])*i)

    # 年齢、年収、MCMCカラムでデータフレーム作成
    pred = pd.DataFrame({'X':i, 'Y':y_salary, 'd_type':'mcmc'})
    
    # 最初は観測データと結合
    if i==24:
        df = pd.concat([obs, pred], axis=0) 
    else:
        df = pd.concat([df, pred], axis=0)

# 整数に変換
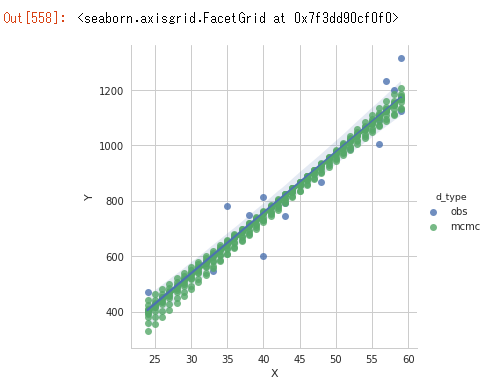
df.iloc[:, 0:2] = df.ix[:, 0:2].astype(int)
print(df)

# プロット
sns.lmplot(x='X', y='Y',  hue='d_type', truncate=True, size=5, data=df)

（インデックス汚いのはご愛嬌）

見にくいｗが、MCMCによる乱数のばらつきはあるものの、うまく観測データに当てはめられている。

##P51のrun-model4-4。

それでは4節最後のモデルをPythonで書いてみる。

python

# P51 run-model4-4

# 都度コンパイルするのは手間なので、pickleで保存しておく関数（引数はStanモデル、普通のコンパイルでも問題なし）
def StanModel_cache(model_code, model_name=None, **kwargs):
    """Use just as you would `stan`"""
    # 公式の'ascii'ではうまくいかないので、'utf-8'に変更
    code_hash = md5(model_code.encode('utf-8')).hexdigest()
    if model_name is None:
        cache_fn = 'stan_pkl/cached-model-{}.pkl'.format(code_hash)
    else:
        cache_fn = 'stan_pkl/cached-{}-{}.pkl'.format(model_name, code_hash)

    try:
        sm = pickle.load(open(cache_fn, 'rb'))
    except: #tryで例外が発生すれば、smを書き込み
        sm = StanModel(file=model_code)
        with open(cache_fn, 'wb') as f:
            pickle.dump(sm, f)
    else: # tryで例外が発生しなければ、"Using cached StanModel"をプリント
        print("Using cached StanModel")
    return sm

#compile⇒上記関数にモデルを渡す
model = StanModel_cache(model_code='RStanBook/chap04/model/model4-4.stan')

コンパイルは時間がかかるので、ネットから上記関数を拝借した。便利。

4-4モデルでは変数の追加がされているので、Python側でも対応する変数を辞書に追加しておく。

python

data = pd.read_csv('RStanBook/chap04/input/data-salary.txt')

#stan_data
stan_data = data.to_dict('list')

#追加された変数
X_new = np.arange(24, 60, 1)
stan_data.update({'N':len(data), 'X_new':X_new, 'N_new':len(X_new)})

print(stan_data)

MCMCサンプリングは特に変化なく、さっきと同じ感じで。
なんとなくmodel.samplingでパラメータ指定をしてみている。

python

# 保存したコンパイル済みのモデルを取り出す
with open('stan_pkl/cached-model-544b12297f135a52bb35c73496f1662d.pkl', 'rb') as f:
    model = pickle.load(f) 

# MCMCサンプリング    
fit_nuts = model.sampling(data = stan_data, seed=1234, warmup=1000, chains=4)

# サンプリング結果を保存（なくても大丈夫）
with open('stan_pkl/fit20171129.pkl', 'wb') as f:
    pickle.dump(fit_nuts, f)

#MCMCサンプリングの結果を抽出
ms = fit_nuts.extract(permuted=False, inc_warmup=True)

#ウォームアップ（バーンイン）のサイズを取得
iter_from = fit_nuts.sim['warmup']

#ウォームアップの区間を省いた区間
iter_range = np.arange(iter_from, ms.shape[0])

#各変数名を取得
paraname = fit_nuts.sim['fnames_oi']

#全て描画したいので、こちらを使う
iter_start = np.arange(0, ms.shape[0])

print(iter_from)
print(iter_start)
print(ms.shape[0])
print(fit_nuts.sim)

サンプリングされたデータがかなり増えている。
これは'transformed parameters'と'generated quantities'に記載した回帰式の結果が追加された為である。
最初の例ではPythonで書いていた回帰式を今回はStanのコードに書いているので、コンパイル⇒データを渡してサンプリングを行うだけで、各年齢における年収のサンプリング結果を返してくれるのだ。
よって、今回のモデルではデータを渡してあげるだけで、先ほどと同じ計算をStan側で処理している。

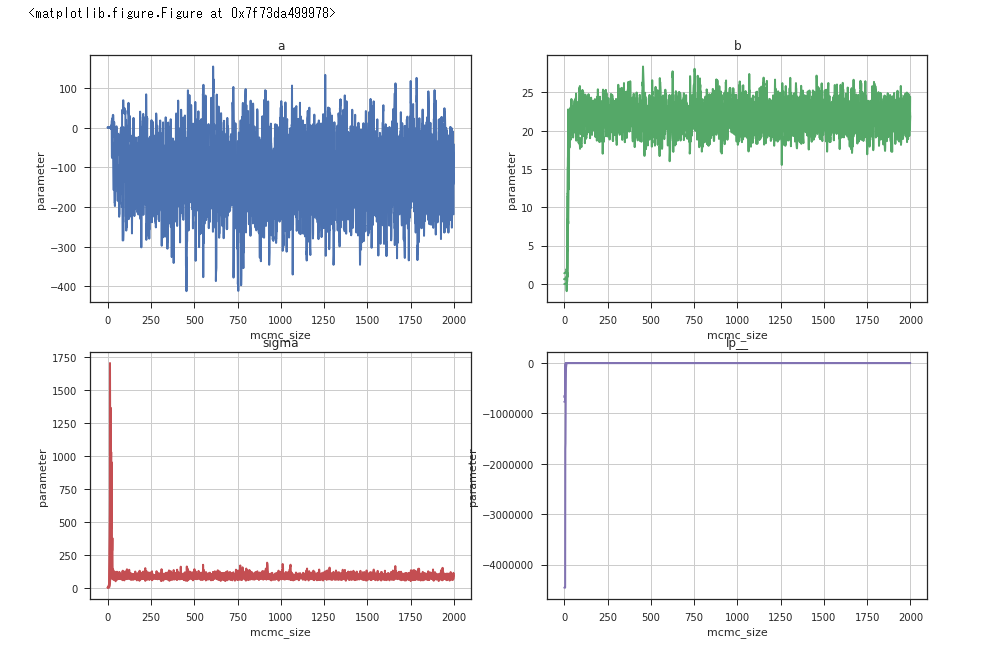
それではMCMCサンプリング収束の様子を描画してみる。
全部は多すぎるので、とりあえず9個。

python

# seabornおまじない
palette = sns.color_palette()
sns.set(font_scale=1)
sns.set_style("ticks")
sns.despine(offset=10, trim=True)
fig,axes  = plt.subplots(nrows=3, ncols=3, figsize=(15,10))

for i in range(3):
    for j in range(3):
        if i>1: l=6
        else: l=0
        axes[i,j].plot(iter_start, ms[iter_start, :, i*3+j], 
                       linewidth=2, color=palette[i*3+j-l])
        axes[i,j].set_title(paraname[i*3+j])
        axes[i,j].set_xlabel('mcmc_size')
        axes[i,j].set_ylabel('parameter')
        axes[i,j].grid(True)

fig.show()

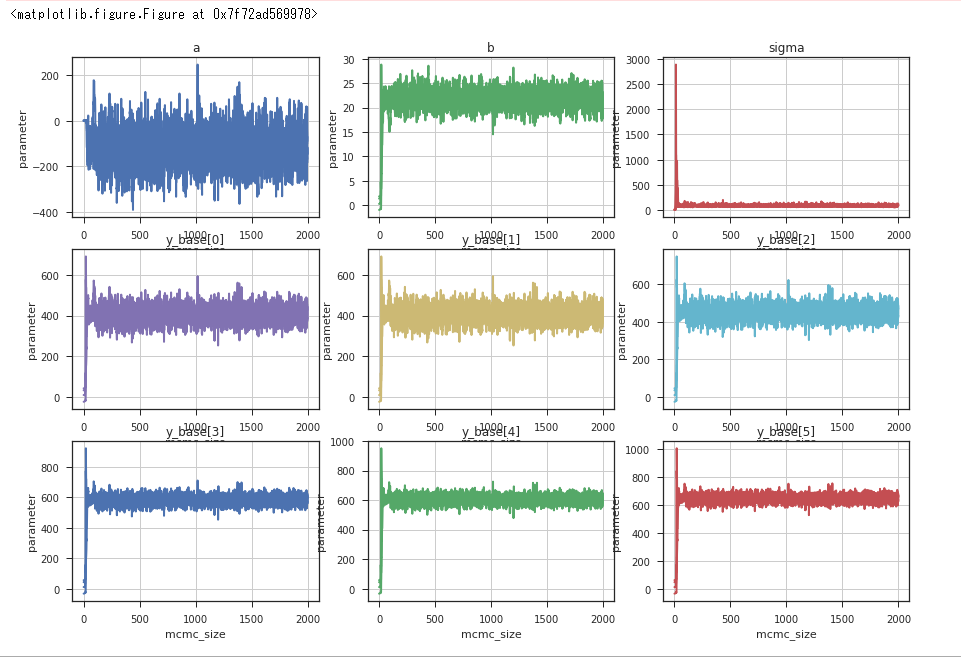
データセットが同じなので係数はほぼ変わらず。追加されているのはサンプリングされたa, b, sigmaの事後分布から導かれた年齢毎の年収の回帰結果である。（y_base[n]）
24歳～29歳のデータだが、徐々に年収が上がっているのがわかる。

4-4のStanモデルでは、MCMCによって求まったa, b, sigmaの事後分布を使い、より現実に即した年収の予測結果を算出する式がgenerated quantitiesに書かれている。（正規分布で誤差も含めている）
上記トレースプロットではそちらを端折ったｗので、予測結果と観測データを比較してみる。

python

# 分位点
qua = [2.5, 25, 50, 75, 97.5]

# stanモデル内で計算した事後分布からの回帰結果を取得
for i in range(59, 95, 1):
    if i==0 :
        df = pd.DataFrame({'salary':np.percentile(ms[iter_range, :, i], q=qua), 'age':i-35, 'd_type':'mcmc'})
    else:
        tmp_df = pd.DataFrame({'salary':np.percentile(ms[iter_range, :, i], q=qua), 'age':i-35, 'd_type':'mcmc'})
        df = pd.concat([df, tmp_df], axis=0)
        
# 観測データを結合 
obs = pd.DataFrame({'salary':data['Y'], 'age':data['X'], 'd_type':'obs'})
df = pd.concat([df, obs], axis=0)

# 整数に変換
df.iloc[:, [0,2]] = df.ix[:, [0,2]].astype(int)
print(df)

# プロット
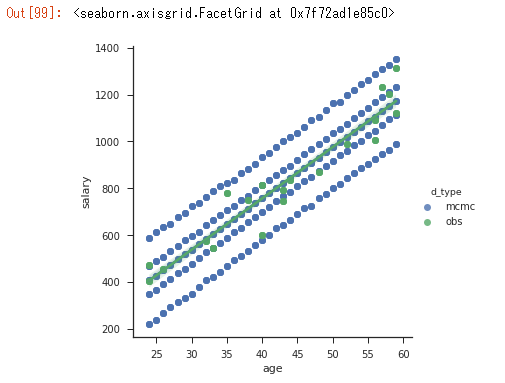
sns.lmplot(x='age', y='salary',  hue='d_type', truncate=True, size=5, data=df)

分位点を抽出して95%信頼区間と第1~3分位点をプロットしている。
結果は下記の通り。

良い感じに観測データが信頼区間に収まっているので、うまく回帰できたといえるだろう。
もっとグラデーションつけて信頼区間を表現したいのだが、あれはどうやるんだろｗ

以上、4節の単回帰についてRからPythonへの置き換えが完了した。
コード自体はシンプルなのでそれほど苦労しないが、描画をもっと美しくできるようにしたいな。。

続いて5節の重回帰もやる予定。