E試験 2024#2 シラバスメモ③-1 深層学習の基礎-最適化/正則化

E試験のシラバスとその概要をメモしたものです。
各サイトや生成AIに聞いたもののツギハギです。

シラバスは2024#2に準拠しています

本記事は３．深層学習のうち
‐ 順伝播型ネットワーク

• 深層モデルのための最適化
• 深層モデルのための正則化
  までについてとなります。
  試験範囲外部分は割愛しています。

順伝播型ネットワーク

パーセプトロン・多層パーセプトロン

１個分のパーセプトロンは $活性化関数(\sum{x_k\cdot w_k+b})$ という形になる
活性化関数は後述
この「重み」「バイアス」の値を学習の中で調整していくことによって制度の高い予測を目指していく。

多層パーセプトロンはこのパーセプトロンを組み合わせたもの

出力層と損失関数

損失関数

予測した値と実際の値の乖離具合を評価する関数
「学習を行う」とはこの関数の乖離具合が最小になることを目指すように調整していくことを指す。

回帰問題で使う損失関数

回帰＝量的変数等の数値の大きさを予測させる問題

MAE
$\text{MAE}=\frac{1}{n}\sum_{i=1}^{n}|\hat{y}_i-y_i|$ 　※$\hat{y}:予測した値 y:正解値$
単純に正解と予測値の誤差を総和したもの

• MSE
  いわゆる最小二乗法
  $\text{MSE}=\frac{1}{n}\sum_{i=1}^{n}(\hat{y}_i-y_i)^2$ 　※$\hat{y}:予測した値 y:正解値$
  正解と予測値の誤差の二乗を総和したもの
• RMSE
  MSEの平方根を取ったもの
  $\text{RMSE}=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(\hat{y}_i-y_i)^2}$
  MSEだと二乗する関係で学習データと単位が合わないという問題があるので元に戻してあげている

MAEとMSE/RMSEの主な違いとしてはバラつきの捉え方
MSEは誤差が二乗されるためより中心から外れたものがより強調される(いわゆる分散をとっている)。
悪く言うと外れ値があった時に影響が大きく出てしまう。

分類問題で使う損失関数

分類問題=不良品かそうでないかのような問題。他クラス分類ならば犬か猫か兎かのような問題。

• 二値クラス分類
  つまり答えがtrueかfalseか(1か0)となる問題
  y:予測した値 t:正解の値
  $バイナリクロスエントロピー=-(t\log{y}+(1-t)\log{(1-y)})$
  これはt=1の時右側は0になって消える。t=0の時左側が消える
  つまり以下と同義

バイナリクロスエントロピー = \left\{
\begin{array}{ll}
\log{y} & (t = 0) \\
\log{(1-y)} & (t \neq 0)
\end{array}
\right.

yの取りうる値は0.0～1.0となる。
パーセプトロンの結果を0.0～1.0に丸めるために出力層の活性化関数にシグモイド関数を使用する。

多クラス分類

他クラス分類はone-hotベクトルで答えを表す
例えば
犬=[1,0,0]
猫=[0,1,0]
兎=[0,0,1]
のようにあらわす。

対して予測した値は[0.0～1.0, 0.0～1.0, 0.0～1.0]のように同じ大きさのベクトルに0.0～1.0が入った結果となり。各要素を総和すると1になる。

コスト関数にはクロスエントロピーを使用する
$クロスエントロピー=-\sum_{i=1}^{n}{t_i\log{y_i}}$

パーセプトロンの結果を0.0～1.0に丸め、各要素の総和を1とするために出力層の活性化関数にソフトマックス関数を使用する。

マルチラベル分類

多値クラス分類は出力の総和は1になり、その中の最大を見る等して答えは1つになるが。(犬、猫、兎のうちのどれかを予測の結果として出すが)
マルチラベル分類は二つ以上の答えを出す。
バイナリクロスエントロピーを出力層でクラスの数だけ用いる、活性化関数はシグモイド関数。(故にソフトマックスとは違って出力の総和は1とはならない。)

順序回帰

活性化関数

各パーセプトロンの入力×重みの総和に対して適用される関数。
中間層と出力層で使用すべき活性化関数が違う。

中間層で使われる活性化関数は出力の表現の自由度をあげるために使用する
出力層で使われる活性化関数は望む出力の形に丸める意味が強い。

個人的には出力層の活性化関数は別の名前にした方がいいと思う・・・出力関数とか

後述するが最適化の際には微分が必要なので微分した式も載せる。

シグモイド関数

中間層、出力層に用いられるが、
後述の理由から最近では中間層にはあまり用いられない。

0.0～1.0の間で
$y = \cfrac{1}{1 + \exp(-x)}$
　$=\cfrac{\exp(x)}{1+\exp(x)}$
※exp(-x)=$e^{-x}$

微分した式は

$\cfrac{\partial y}{\partial x} = y(1 - y)$

(出所：https://qiita.com/kuroitu/items/73cd401afd463a78115a)

このように微分した結果の最大値が0.25となるため、層が深くなると逆伝播時に値がどんどん小さくなっていき、最終的に重みの更新がされなくなり学習が停滞してしまう。
この問題を勾配消失問題という

ソフトマックス関数

他クラス分類の出力層に使用する
$y_i = \cfrac{\exp(x_i)}{\sum_{k=1}^{n}{\exp(x_k)}} \quad (i = 1, 2, \ldots, n)$

$y_1+y_2...+y_n$は1となる

微分した形は

\cfrac{\partial y_i}{\partial x_k} = \left\{
\begin{array}{ll}
y_i(1-y_i) & (i = k) \\
-y_iy_k & (i \neq k)
\end{array}
\right.

温度スケーリング、温度パラメータ

ソフトマックス関数に適用する前に「温度パラメータT」で割る
$$
\large
\begin{align}
\mathrm{Softmax}(u_k) = \frac{\exp{(u_k/T)}}{\displaystyle \sum_{j=1}^{K} \exp{(u_j/T)}} \quad (1)
\end{align}
$$
T=1の時ソフトマックス関数と一致する
T<0の場合より極端に、各結果の差が際立つ形になる。
T>1の場合より一様分布に近い形になる。

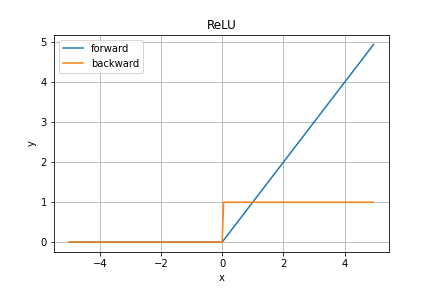
ReLU, Leaky ReLU

ReLU関数は中間層で使用される活性化関数

順伝播の数式は

y = \left\{
  \begin{array}{cc}
    x & (x \gt 0) \\
    0 & (x \le 0)
  \end{array}
\right.

微分した形は

\cfrac{\partial y}{\partial x} = \left\{
  \begin{array}{cc}
    1 & (x \gt 0) \\
    0 & (x \le 0)
  \end{array}
\right.

微分した結果が1となるので勾配消失が起こりにくい。

Leaky ReLU

中間層で用いられる活性化関数
ReLUは負の入力時に勾配が0となるため、学習が進まないため負の入力の時に小さな傾きを足した関数。

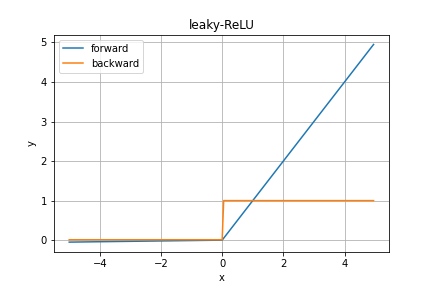
y = \left\{
  \begin{array}{cc}
    x & (x \gt 0) \\
    0.01x & (x \le 0)
  \end{array}
\right.

微分した値は

\cfrac{\partial y}{\partial x} = \left\{
  \begin{array}{cc}
    1 & (x \gt 0) \\
    0.01 & (x \le 0)
  \end{array}
\right.

GELU

中間層で使用される活性化関数
GPTやBERTにも採用されている。

(出所：https://cvml-expertguide.net/terms/dl/layers/activation-function/relu-like-activation/gelu/)
$\text{GELU}(x) = x \Phi(x) = x \cdot \frac{1}{2} \left[ 1 + \text{erf} \left( \frac{x}{\sqrt{2}} \right) \right]$

tanh

中間層で利用される活性化関数

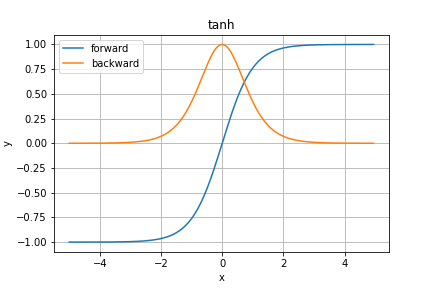
-1.0から1.0までの値をとる

y = \tanh x = \cfrac{e^x - e^{-x}}{e^x + e^{-x}}

微分は

\cfrac{\partial y}{\partial x} = \textrm{sech}^2 x = \cfrac{1}{\cosh^2 x} = \cfrac{4}{(e^x + e^{-x})^2}

微分した値が1なのでシグモイド関数よりは勾配消失が起きにくいが起きないわけではない。

深層モデルのための最適化

基本的なアルゴリズム

コスト関数の全体の谷がどこにあるかは全数検査しない限り不可能なので
現在の損失関数の値を元に重みを調整して探していく必要がある。
損失関数を偏微分することで「勾配」を求める。
勾配の傾きの大きさで重みの調整方向と移動量を決め、新たな重みに更新していく。

具体的にどう重みを調整していくかは以下の「最適化関数」を用いて調整していく。

誤差逆伝播法 誤差逆伝播法

連鎖律(チェーンルール)

逆伝播の数学的基礎

合成関数$f(x(u,v), y(u,v))$の様なものがあったとして偏微分「$\cfrac{\delta f}{\delta u}$」を考えたい。$f(u,v)=(u^2+v^2)\sin(uv)$で$x=u^2+v^2$　$y=\sin(uv)$ $f(x,y)=xy$と置いたイメージでuについて偏微分

uに関する経路は二つある


これらを足し合わせたものが
$\cfrac{\delta f}{\delta u}=\cfrac{\delta f}{\delta x}\cfrac{\delta x}{\delta u} + \cfrac{\delta f}{\delta y}\cfrac{\delta y}{\delta u}$
(出所：https://mathlandscape.com/partial-derivative-composite/)

自動微分・計算グラフ

パラメータ最適化(Optimizer)の変遷

(出所：https://i-main.net/emmanote-ai-optimizer/)

確率的勾配降下法（SGD）

学習データを毎回ランダムにシャッフルして適当なサイズ(ミニバッチ)に分割。
１回のミニバッチごとに上記の方法で重みパラメータを更新し絵行く

$W_t:=W_t-Lr\nabla\text{E}(W_t)$　　(※「:=」は代入記号。$W_t$の値を右辺の式で更新する)
要は元の重みを勾配の大きさに応じて更新する。
ただしそのまま更新するのではなくLr=学習率をかける。
学習率は適当な係数で0.01とかが入る。

学習率はハイパーパラメータと呼ばれるもののひとつで、人間が経験則であったりトレーニングの中の試行錯誤の中で決めていく。
学習率が小さすぎると単純に学習が遅くなるという他に、「局所解」(上記のグラフの一番深い谷ではなく、途中にある細かい谷)に陥って学習が進まなくなる。
学習率が大きすぎると上記のグラフで言うと、一回の移動で一番深い谷を通りこして、いつまでもいったりきたりして学習が収束しない可能性がある。

Pathological Curvature

Pathological Curvatureとは以下の図のような鋭いくぼみを持つ形状のことで、SGDだとオーバーシュート(1度の更新が大きすぎること)して振動を起こしてしまうため最小値にたどり着くのが遅いです。

この振動を抑えて以下の様な理想の経路をたどらせる手法としてモメンタムやRMSpropがある

(出所：https://qiita.com/omiita/items/1735c1d048fe5f611f80)

モメンタム

モメンタムは勾配で導き出された値にいきなり更新するのではなく
前回の勾配のベクトル方向と今回の勾配で更新された値の内積をとる

前の更新の速度を利用しつつ慣性がついた状態で今回の更新を行うイメージ

前回の速度
$v_{t+1} := \alpha v_{t}-Lr\nabla(W_{t-1})$　※α:モメンタム係数 Lr:学習係数
速度を意識して重み更新
$W_{t+1} := W_{t} + v_t+1$

(出所:https://i-main.net/emmanote-ai-optimizer/)

ネステロフのモメンタム Nesterov’s Accelerated Gradient

モメンタムは前回の勢いが誤った方向の場合オーバーシュートする懸念があった。

勾配を求める箇所を(W_{t-1}+\alpha v_t)新しい箇所で計算することによってオーバーシュートを置きにくくする
$v_{t+1} := \alpha v_{t}-Lr\nabla(W_{t-1}+\alpha v_t)$　※α:モメンタム係数 Lr:学習係数
$W_{t+1} := W_{t} + v_t+1$

(出所:https://i-main.net/emmanote-ai-optimizer/)

適応的な学習率を持つアルゴリズム

学習率が一定だと、答えから遠い時には学習が進まなく、答えから近づいた時は発散するリスクがある
学習率を学習状況に応じて変化させるというモチベーションの手法がAdagradとRMSProp

AdaGrad

学習率\alphaを以下のように変化させる
$h_{t+1}:=h_t+\nabla E(W_t) \bigodot \nabla E(W_t)$
$\alpha_t := \alpha_0\cfrac{1}{\sqrt{h_{t+1}}+\epsilon}$　※$\epsilon$は分母が0にならないように足す十分小さな値
$W_{t+1}:=W_t - \alpha_t\nabla E(W_t)$

hに過去の方向がアダマール積で蓄積されて行くため、その方向のに対する移動量がどんどん小さくなってくる。
が、0に近づきすぎて学習が進まなくなる可能性もある。

RMSProp

Adagradの過去の値を全て累積するのではなくβで適度に案分する。

$h_t+1:=\beta h_t + (1-\beta)\nabla E(W_t) \bigodot \nabla E(W_t)$
以降はAdagradと同様

Adam

モメンタムと、Adagrad/RMSpropをかけ合わせたアルゴリズム。
$m_{t+1}:=\beta_1 m_t + (1-\beta_1)\nabla(W_t)$　※モメンタム
$v_{t+1}:=\beta_2 m_t + (1-\beta_2)\nabla(W_t) \bigodot \nabla(W_t)$　※RMSProp
$\hat{m}=\cfrac{m+1}{1-\beta^{t}_1}$
$\hat{v}=\cfrac{v_t+1}{1-\beta^{t}_2}$

$W_{t+1}=W_t-\alpha \cfrac{\hat{m}}{\sqrt{\hat{v}}+\epsilon}$

パラメータの初期化戦略

重み等のパラメータは基本乱数や固定値で初期化するが、初期値の設定によって学習の効率が良くなる

• Xavier法/Glorot法
  前層のノード数がnの場合、$\cfrac{1}{\sqrt{n}}$を標準偏差としたガウス分布からの乱数で重みの初
  期値を決める手法。
  主にシグモイド関数やtanh関数を活性化関数に使う際に使用する。

• Kaiming法/He法
  前層のノード数がnの場合、$\sqrt{\cfrac{2}{n}}$を標準偏差としたガウス分布からの乱数で重みの初
  期値を決める手法。
  主にReLUに使う際に使用する。

深層モデルのための正則化

パラメータノルムペナルティー

L1正則化、スパース表現、L2正則化、weight decay
https://qiita.com/hokutoh/items/c170d0c3447d01e57186#%E6%AD%A3%E5%89%87%E5%8C%96

確率的削除

ドロップアウト、ドロップコネクト

• ドロップアウト
  学習する際に、中間層のノードをランダムに無効にして学習を行い過学習を減らす手法。
• ドロップコネクト
  ドロップアウトはノードを削除する形だったが、ドロップコネクトは接続を削除する

学習時に違うモデルのようにふるまうのでアンサンブル学習の様な効果が見込まれ、過学習を防ぎ汎化性能が上がる。
また、省いているノード/接続があるわけなので計算量削減も期待できる。

ReLUやtanhの場合ドロップコネクトの方が性能がいいと言われている。

陰的正則化

確率的勾配降下法(SGD; Stochastic Gradient Descent method)では「全てのサンプルを同時に学習させる」ではなく、「サンプルをランダムに選び学習させる」ということが行われる。
この際に目的関数が変化することで正則化のような効果が得られると解釈が可能である。このように「サンプルをランダムに選び学習させる」ことによって得られる「正則化効果」を「陰的正則化」という。

早期終了

指定回数学習を行うのではなく学習段階でなんらかの値(accuracyやloss等)が閾値を下回ったら学習をその時点で止めてしまう
過学習を防ぐ効果がある。

出所：https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-deep-learning-tips-and-trick