はじめに

Kaggleで人気の機械学習のチュートリアルをやってみたので共有します。
このチュートリアルでは、データの前処理について紹介していきます。

チュートリアルの原文はこちらです。
Comprehensive data exploration with Python

使うデータはこちらでダウンロードしてください。
House Prices: Advanced Regression Techniques / Data

このデータは、住宅の販売価格を予測するデータ分析コンペで使用されたものです。

導入

このチュートリアルでやることは次の通りです。

1. 問題を理解する
2. 予測する変数(SalePrice)について詳しく見る
3. 変数同士の関係について詳しく見る
4. 欠損値・外れ値の取り扱い
5. 解析の事前確認

まず、ライブラリとデータを読み込んで、データの中身を見ておきます。

#invite people for the Kaggle party
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from scipy.stats import norm
from sklearn.preprocessing import StandardScaler
from scipy import stats
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline

#bring in the six packs
df_train = pd.read_csv('../input/train.csv')

#check the decoration
df_train.columns

出力

Index(['Id', 'MSSubClass', 'MSZoning', 'LotFrontage', 'LotArea', 'Street',
       'Alley', 'LotShape', 'LandContour', 'Utilities', 'LotConfig',
       'LandSlope', 'Neighborhood', 'Condition1', 'Condition2', 'BldgType',
       'HouseStyle', 'OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd',
       'RoofStyle', 'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType',
       'MasVnrArea', 'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual',
       'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinSF1',
       'BsmtFinType2', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', 'Heating',
       'HeatingQC', 'CentralAir', 'Electrical', '1stFlrSF', '2ndFlrSF',
       'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath',
       'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr', 'KitchenQual',
       'TotRmsAbvGrd', 'Functional', 'Fireplaces', 'FireplaceQu', 'GarageType',
       'GarageYrBlt', 'GarageFinish', 'GarageCars', 'GarageArea', 'GarageQual',
       'GarageCond', 'PavedDrive', 'WoodDeckSF', 'OpenPorchSF',
       'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'PoolQC',
       'Fence', 'MiscFeature', 'MiscVal', 'MoSold', 'YrSold', 'SaleType',
       'SaleCondition', 'SalePrice'],
      dtype='object')

全部で81個の特徴があります。
例えば、Streetは住宅へのアクセスのタイプで、砂利道や舗装などのデータが含まれています。

1. 問題を理解する

まず、問題を理解するために変数を一つずつ見て、本当に価格に関連性がありそうなのかを考えます。
これによって、データ分析における「第六感」を養うことができます。

本当に必要な変数なのか？
例えば、家を購入する時にベニヤ板の種類(MasVnrType)を気にすると思いますか？
その変数はどれくらい影響があるのか？
例えば、「絶対、このベニヤ板がいい！」とか「できれば、このベニヤ板がいいな。」とか。
また、変数同士で関係がないか？
例えば、似たような意味合いである住宅の平坦度(LandContour)と住宅の傾斜(LandSlope)とか。

このチュートリアルでは、販売価格に関係しそうな変数を以下の４つに絞って見ていきます。
（本来は、他の変数も分析する必要があります。）

OverallQual：素材・完成度
YearBuilt：建設日
TotalBsmtSF：地下の広さ
GrLivArea：地上の広さ

2. 予測する変数(`SalePrice`)について詳しく見る

予測するSalePriceについて、詳しく見て見ます。

#descriptive statistics summary
df_train['SalePrice'].describe()

出力

count      1460.000000
mean     180921.195890
std       79442.502883
min       34900.000000
25%      129975.000000
50%      163000.000000
75%      214000.000000
max      755000.000000
Name: SalePrice, dtype: float64

平均価格や最低価格、最大価格などが確認できます。

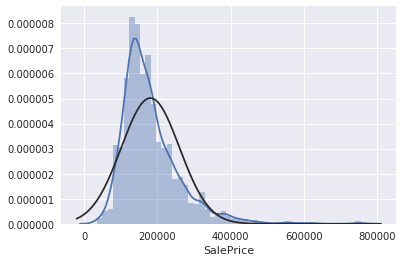
ヒストグラムを書いて見ます。

#histogram
sns.distplot(df_train['SalePrice']);

正規分布ではなく、少し歪んでいるようです。
また、ピークも確認できます。

歪度(どれくらい非対称性か)と尖度(どれくらいピークが鋭いか)を見てみます。

#skewness and kurtosis
print("Skewness: %f" % df_train['SalePrice'].skew())
print("Kurtosis: %f" % df_train['SalePrice'].kurt())

出力

Skewness: 1.882876
Kurtosis: 6.536282

2-1.　`SalePrice`との関係

単純に、先ほど選んだ４つの変数との関係をプロットして見てみます。

OverallQual：素材・完成度
YearBuilt：建設日
TotalBsmtSF：地下の広さ
GrLivArea：地上の広さ

「GrLivArea」との関係

#scatter plot grlivarea/saleprice
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

線形の関係性がありそうです。

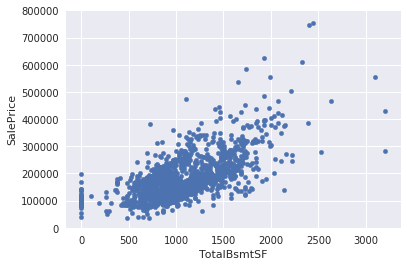
「TotalBsmtSF」との関係

#scatter plot totalbsmtsf/saleprice
var = 'TotalBsmtSF'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

線形の関係性がありそうです。

「OverallQual」との関係

#box plot overallqual/saleprice
var = 'OverallQual'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);

明らかに、関係がありそうです。

「YearBuilt」との関係

var = 'YearBuilt'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
plt.xticks(rotation=90);

強い傾向ではないが、新しい住宅の方がSalePriceが高いように見えます。

※ このデータの販売価格が、一定価格であるかは分からない。インフレによって販売価格は変化することに注意。

2-2.　ここまでの要約

地上・地下の広さと販売価格の関係は、線形的で正の相関がありそう
素材・完成度、建設日と販売価格の間にも、関係性がありそう

3. 変数同士の関係について詳しく見る

今までは、主観的に変数を見てきました。
次は、客観的に変数を見ていきます。

見るものは、以下の３つです。

全変数の相関行列
SalePriceと相関が高めの変数(トップ１０)に絞った相関行列
SalePriceと相関が高めの変数(トップ１０)に絞った散布図

1. 全変数の相関行列

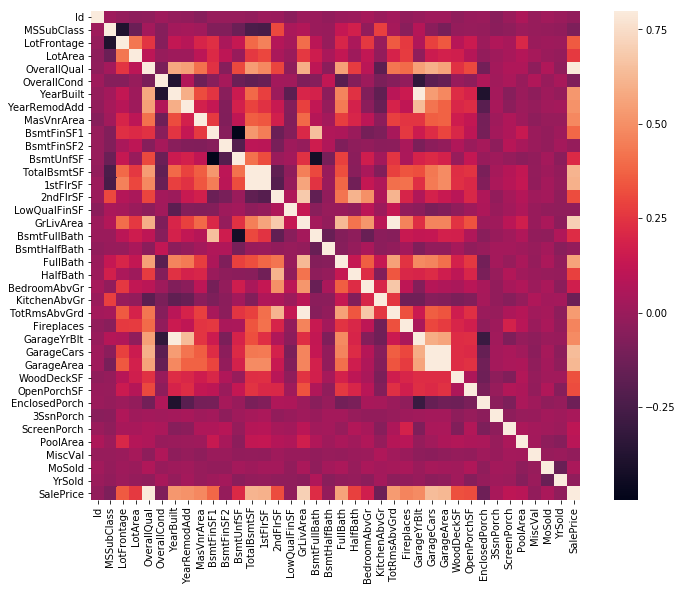
まずは、全変数同士の相関行列を見てみます。
ちなみに、この相関行列はヒートマップとも呼ばれます。

#correlation matrix
corrmat = df_train.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);

この相関行列から、互いに相関している変数を見つけることができます。

例えば、Garange系の変数は、互いにGarage系の変数に相関していることが確認できます。
このことは、ガレージに入る車の数はガレージの広さによって決まると考えられるからです。

この様に、互いに相関している変数を多重共線性を持つと言います。

2. SalePriceと相関が高めの変数(トップ１０)に絞った相関行列

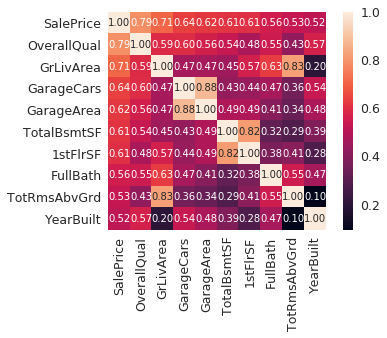
次に、SalePriceと相関の高い変数トップ１０に注目して、相関行列を見てみます。

#saleprice correlation matrix
k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(df_train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()

これにより、どの変数がSalePriceに関係ありそうなのかを見ることができます。

厳密には、YearBuiltのような変数には時系列解析をするべきであると思われますが、今回はそのまま続けます。

3. SalePriceと相関が高めの変数(トップ１０)に絞った散布図

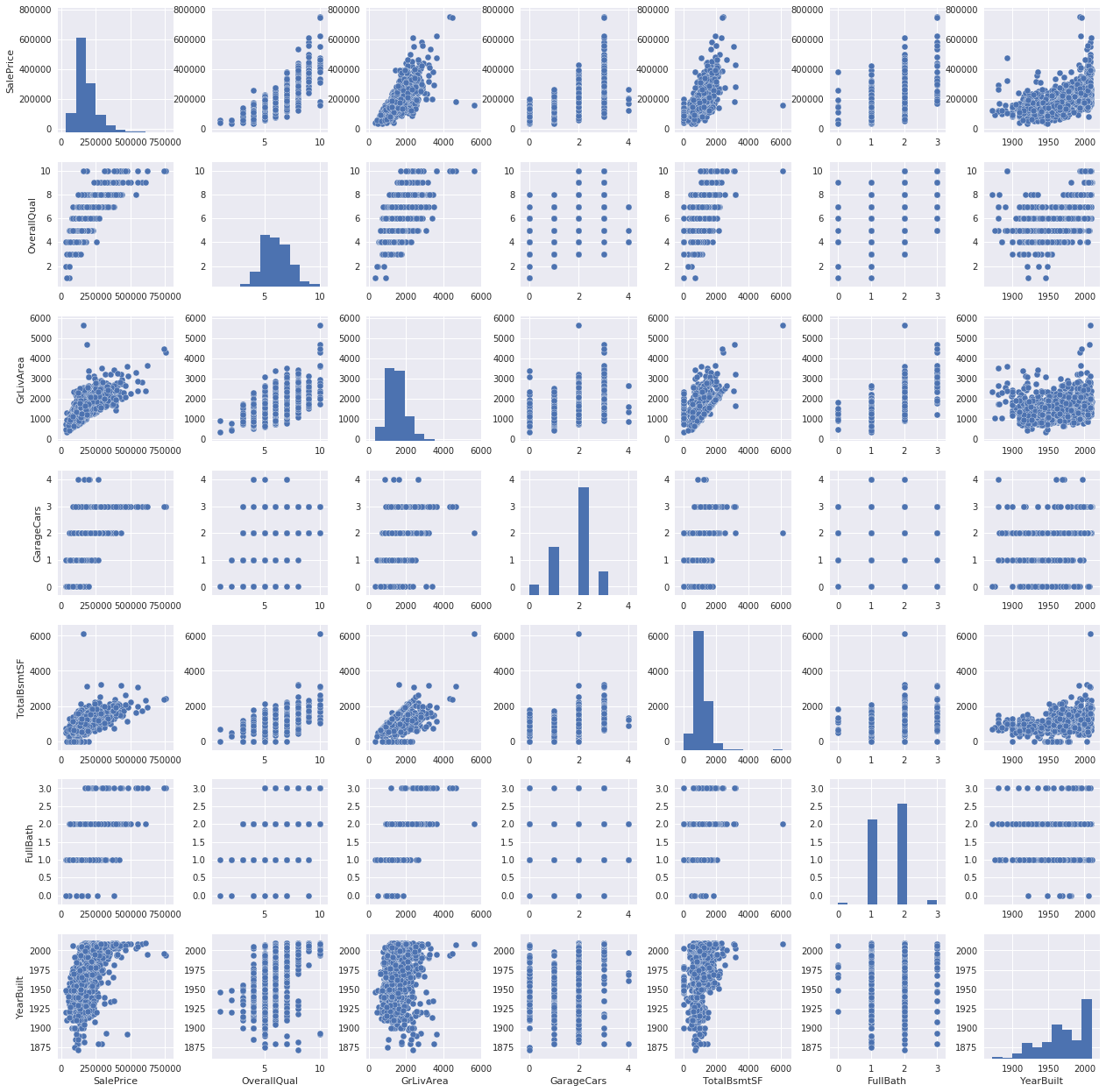
最後に、散布図を見てみます。

#scatterplot
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(df_train[cols], size = 2.5)
plt.show();

TotalBsmtSFとGrLiveAreaの散布図を見ると、直線的な模様を見ることができます。
この直線より下の点は、予測のための変数としては期待できません。
なぜなら、地上より地下の面積が広いとは、あまり考えられないからです。

SalePriceとYearBuiltの間には、指数関数的な形が示されていることが確認できます。

4. 欠損値・外れ値の取り扱い

データに欠損値・外れ値はつきものですが、そのままでは解析できないので対処していきます。
以下の対処法は、ほんの一例です。

4-1. 欠損値

まず、欠損しているデータについて見ていきます。

#missing data
total = df_train.isnull().sum().sort_values(ascending=False)
percent = (df_train.isnull().sum()/df_train.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)

欠損したデータをどう処理するか考えてみます。

右列のPercent列は、データの欠損率を示しています。
まず、データが１５％以上欠損している変数は削除(解析には使わない)することにします。

次に、Garage系の変数を見ると、値が全て同じことから、同じ物件を参照していると考えられます。
そして、Garage系の変数は、前述したGarageCarsで表現できる(多重共線性)と考えられるため、これも削除します。
同様のロジックで、Bsmt系の変数も削除します。

MasVnrArea(ベニヤ板の面積)とMasVnrType(ベニヤ板の種類)については、それほど重要な変数ではないと考えられます。
なぜなら、これらはYearBuiltとOverallQualと強い相関があるので、MasVnr系の変数を削除しても情報は失われないと考えられるからです。

Electricalについては欠損値が１つだけなので、変数は削除せずに、この１軒の住宅データごと削除することにします。

まとめると、Electrical以外の変数において欠損値を含む変数を削除し、Electricalが欠損している１軒の住宅データを削除します。

#dealing with missing data
df_train = df_train.drop((missing_data[missing_data['Total'] > 1]).index,1)
df_train = df_train.drop(df_train.loc[df_train['Electrical'].isnull()].index)
df_train.isnull().sum().max() #just checking that there's no missing data missing...

出力

4-2. 外れ値

次に、外れ値について見ていきます。
外れ値は予測に影響を及ぼすので、注意を払う必要があります。

4-2-1. 単変量解析

まずは、SalePriceのみについて外れ値を見てみます。
外れ値を調べるには外れ値とする域値を設定する必要があり、その前にデータを標準化します。
ここでの標準化とは、平均０および標準偏差１に変換することを意味します。

#standardizing data
saleprice_scaled = StandardScaler().fit_transform(df_train['SalePrice'][:,np.newaxis]);
low_range = saleprice_scaled[saleprice_scaled[:,0].argsort()][:10]
high_range= saleprice_scaled[saleprice_scaled[:,0].argsort()][-10:]
print('outer range (low) of the distribution:')
print(low_range)
print('\nouter range (high) of the distribution:')
print(high_range)

出力

outer range (low) of the distribution:
[[-1.83820775]
 [-1.83303414]
 [-1.80044422]
 [-1.78282123]
 [-1.77400974]
 [-1.62295562]
 [-1.6166617 ]
 [-1.58519209]
 [-1.58519209]
 [-1.57269236]]

outer range (high) of the distribution:
[[3.82758058]
 [4.0395221 ]
 [4.49473628]
 [4.70872962]
 [4.728631  ]
 [5.06034585]
 [5.42191907]
 [5.58987866]
 [7.10041987]
 [7.22629831]]

この結果から、安い(低い)範囲の住宅は平均0に近いが、高い範囲の住宅はあまり平均０に近くないことが確認できます。
つまり、高い住宅にはばらつきがあるということです。
特に、下の２つ( [7.10041987]と[7.22629831] )は外れ値と考えることができますが、とりあえず今回はそのままにしておきます。

現実を考えても、高級マンションや豪邸など異常に高い住宅があることから想定できます。

4-2-2. 二変量解析

二変量解析は、前述した散布図を使用します。

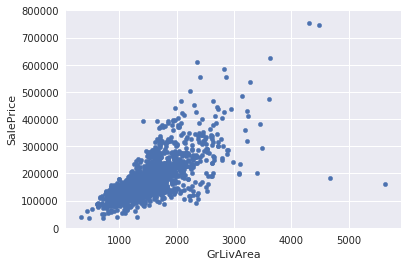
まずは、SalePrice - GrLivArea間で見てみます。

#bivariate analysis saleprice/grlivarea
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

この散布図から、右の方に外れ値が２つあることが確認できます。
おそらくこれらは、土地の安い農家だと思われます。
よって、これら２つのデータは削除します。

#deleting points
df_train.sort_values(by = 'GrLivArea', ascending = False)[:2]
df_train = df_train.drop(df_train[df_train['Id'] == 1299].index)
df_train = df_train.drop(df_train[df_train['Id'] == 524].index)

次に、SalePrice - TotalBsmtSF間で見てみます。

#bivariate analysis saleprice/grlivarea
var = 'TotalBsmtSF'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

TotalBsmtSF > 3000　の値を外れ値としたい気もしますが、そのままにしておきます。
要は、外れ値の定義は感覚です。

5. 解析の事前確認

ここまでで、データ整形を行ってきました。
最後に、SalePriceに多変量解析が適応できるかを確認します。

多変量解析を行う際には、次の4つの前提条件を確認する必要があります。

① 正規性
データが正規分布に従っている方が望まれます。

② 等分散性
全変数において分散が同じレベルであることが望まれます。

③ 線型性
散布図を見て、線形な関係になっていることが望まれます。
前述で、SalePriceとOverallQual・YearBuilt・TotalBsmtSF・GrLivAreaとの線形性を確認しました。

④ 相関誤差の欠如(Absence of correlated error)
時系列データの場合に注意すべきと書いてあるようです。
ちょっと、理解できませんでした。。。(誰か、教えてください。)
とりあえず、原文を載せておきます。

Correlated errors, like the definition suggests, happen when one error is correlated to another. For instance, if one positive error makes a negative error systematically, it means that there's a relationship between these variables. This occurs often in time series, where some patterns are time related. We'll also not get into this. However, if you detect something, try to add a variable that can explain the effect you're getting. That's the most common solution for correlated errors.

③ 線形性は確認済みで、④ 相関誤差の欠如は関係ない(らしい)ので、① 正規性と② 等分散性を確認します。

5-1. 正規性

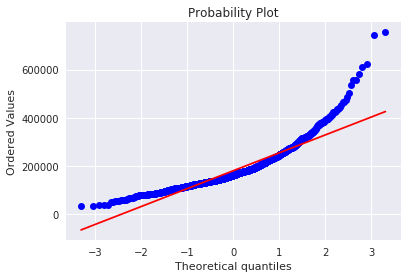
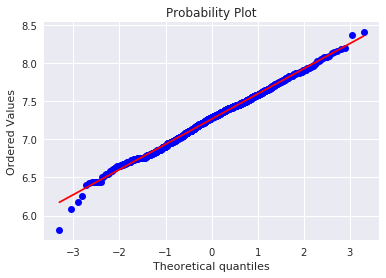
ヒストグラムと正規確率プロットを使って正規性を確認します。
正規確率プロットは、プロットが一直線上に並んでいれば正規分布に従っていると考えられます。

#histogram and normal probability plot
sns.distplot(df_train['SalePrice'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)

グラフを見ると、SalePriceは正規分布にあまり従っていない様です。
ですが、正の歪度を持つ場合は対数変換が有効なのでやってみます。

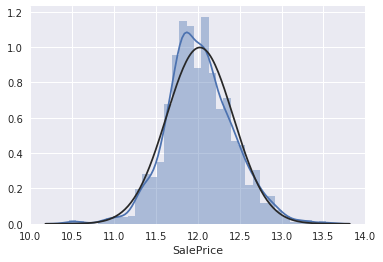
#applying log transformation
df_train['SalePrice'] = np.log(df_train['SalePrice'])
#transformed histogram and normal probability plot
sns.distplot(df_train['SalePrice'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)

うまく正規分布に従った様です。

GriLivAreaについて見てみます。

#histogram and normal probability plot
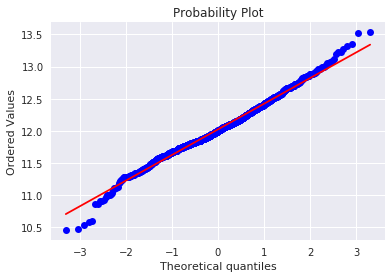
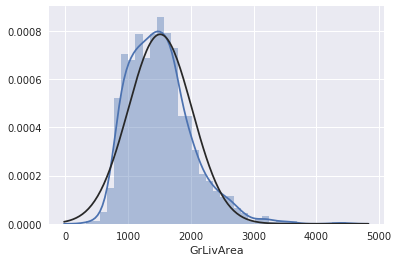
sns.distplot(df_train['GrLivArea'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['GrLivArea'], plot=plt)

同じく、正の歪度がありそうなので対数変換します。

#data transformation
df_train['GrLivArea'] = np.log(df_train['GrLivArea'])
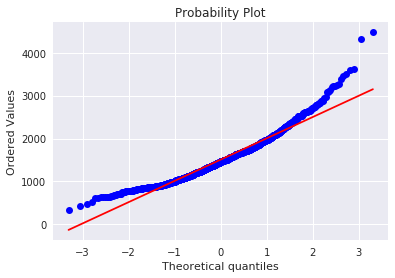
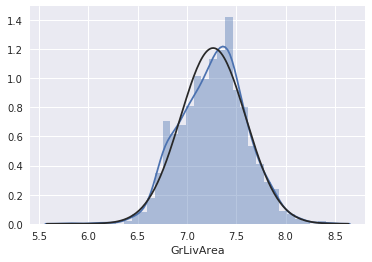
#transformed histogram and normal probability plot
sns.distplot(df_train['GrLivArea'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['GrLivArea'], plot=plt)

うまく正規分布に従った様です。

5-2. 等分散性

言葉での説明が難しかったので、引用した図を載せておきます。

要は、プロットの広がりがどの場所も等しくなることが、等分散性であるといいます。

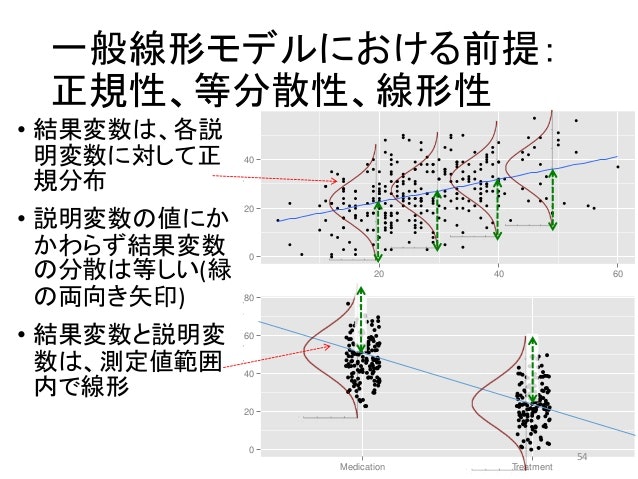
引用：臨床心理学におけるR入門: データハンドリングから統計解析まで

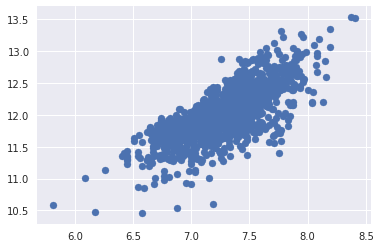
では、対数変換後のSalePriceとGrLivAreaのプロットを見てみます。

#scatter plot
plt.scatter(df_train['GrLivArea'], df_train['SalePrice']);

3. 変数同士の関係について詳しく見るで見た散布図と比較してみると、対数変換後の方が等分散性になっていることが確認できます。

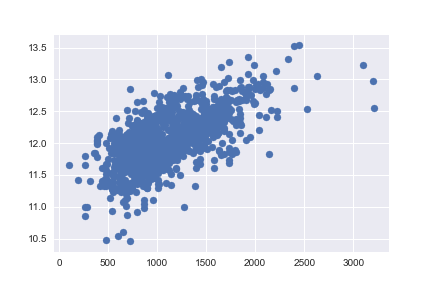
次に、対数変換後のSalePriceと、GrLivAreaのプロットを見てみます。

#scatter plot
plt.scatter(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], df_train[df_train['TotalBsmtSF']>0]['SalePrice']);

等分散性になっていると言えるでしょう。

最後に、カテゴリカル変数を男：０、女：１のように変換して、このチュートリアルは終了です。

#convert categorical variable into dummy
df_train = pd.get_dummies(df_train)

最後に

この様に、長いデータの前処理を行って、やっとモデルの選択・学習へのステップに進むことができます。
ですが、モデルの選択・学習にも様々な手法があり、どれを使うのかはあなた次第です。

ちなみに、変数4つとランダムフォレストを使って簡単な予測を行い、結果をKaggleに提出したところ、スコア(RMSLE:小さい方が良い)が0.17495でした。
予測のサンプルプログラムは、「GitHub」に載せておきます。

また、さらに強力な学習法・アンサンブル学習については、「Pythonでアンサンブル(スタッキング)学習 & 機械学習チュートリアル in Kaggle」で紹介しているので、よければご覧ください。

「データ前処理」- Kaggle人気チュートリアル