MATLABによる宇宙機の軌道伝播（地球-月円制限三体問題におけるNRHOの描画）

Last updated at 2024-10-10Posted at 2024-10-05

アストロダイナミクス分野（軌道設計や最適化など）では、MATLABが広く用いられています。

本記事は、研究室配属前後や軌道をやってみたい方向けかつ、MATLABのライセンスが無料の機関の方向けです。K大学やST大学など、最近は多くの大学で無料になっていると思います。

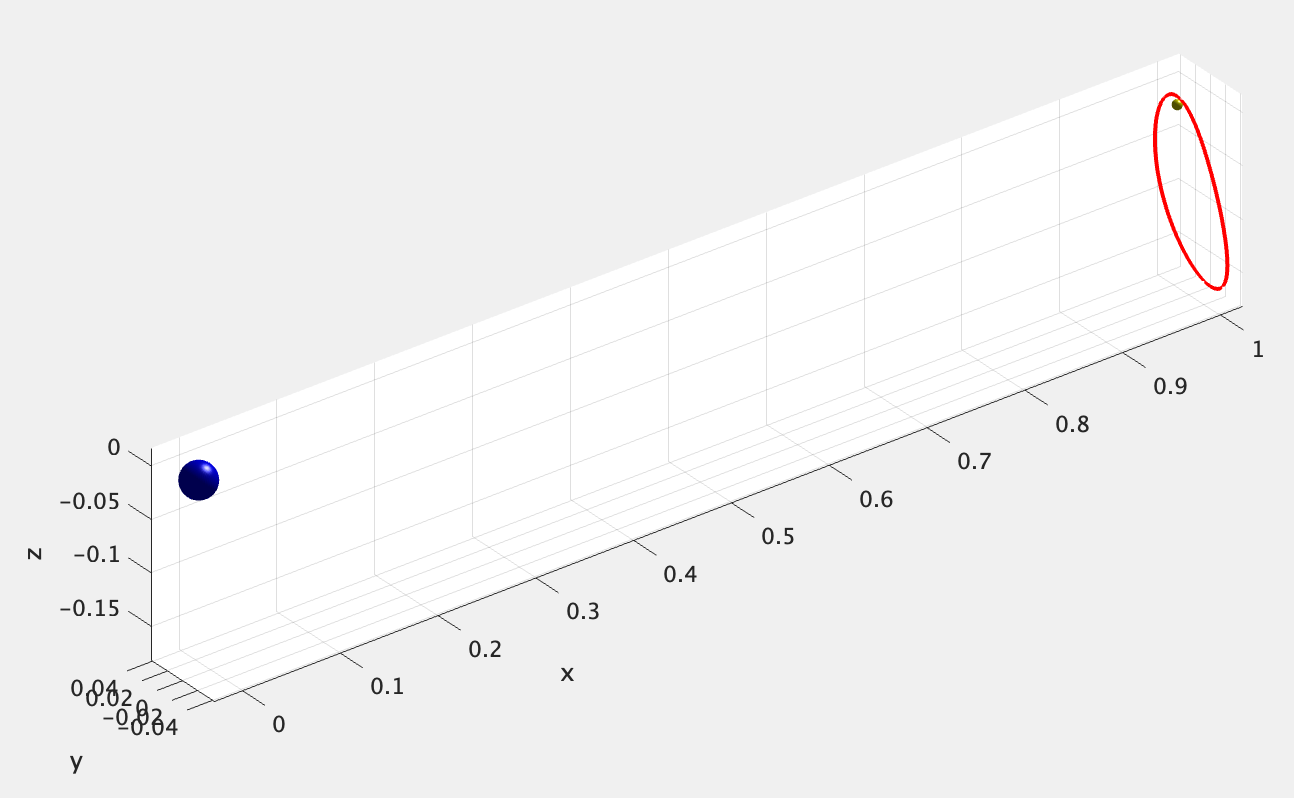
本稿では、円制限三体問題（回転座標系で正規化）の軌道伝播と描画のコードを共有する。
※プロンプトを工夫すれば、ChatGPTでもコードを出すことができます。

宇宙機の運動は微分方程式で表されるため、それを連続的に時間積分すると、宇宙機の軌道を描画することができ、それを軌道伝播という。¹

なお、内容は尾崎さんの記事（https://zenn.dev/naoyaozaki/articles/a3c0b199cdf23f ）において、Julia言語で書かれているもののMATLAB版です。円制限三体問題はこちらの記事（https://qiita.com/hokkaido/items/6d77c5f303f065054edc ）、さらに発展としてこちらのYuriさんの記事（https://qiita.com/Yuricst/items/caf654d92be1d87d2e3d ）も参考にしてください。

要点

軌道伝播の積分は、MATLABのode45が主に使われる
スイングバイなど、精度が求められる軌道では、以下のようなoptionを設定することで精度を上げる。options = odeset('RelTol',1e-12,'AbsTol',1e-12);ode78などの精度の高いモデルを使うことも有効である。
軌道伝播の精度を高めるために、円制限三体問題のように距離や時間の正規化を行う。

※最適化問題などのデバッグをする際に、精度が課題で解けないことがあるので注意してください。

以下のコードをそのままコピペして実行していただければ、軌道伝播と描画ができます。

clear
close all

% Constants
mu = 0.01215058426994;  % Earth-Moon system mass ratio
earth_radius_km = 6371;  % Earth's radius in kilometers
moon_radius_km = 1737;   % Moon's radius in kilometer
distance_earth_moon_km = 384400;  % Average distance between Earth and Moon in kilometers

% Normalized radii
radius_earth = earth_radius_km / distance_earth_moon_km;
radius_moon = moon_radius_km / distance_earth_moon_km;

% Initial conditions
% これは、以下の尾崎さんのZennの記事の値を使用しています。
% https://zenn.dev/naoyaozaki/articles/a3c0b199cdf23f
y0_vec =[0.987384153663276, 0.0, 0.008372273063008, 0.0, 1.67419265037912, 0.0];

% Time span
tspan = [0 2];% （時間は適当, 正規化されているので注意）

% Solve the ODE
options = odeset('RelTol',1e-12,'AbsTol',1e-12);
[t, y] = ode45(@(t, y) cr3bp_ode(t, y, mu), tspan, y0_vec, options);

%% Plot the results
figure(1)
plot3(y(:,1), y(:,2), y(:,3), 'r', LineWidth=2);
hold on
[x_sphere, y_sphere, z_sphere] = sphere(50);
surf(radius_earth * x_sphere - mu, radius_earth * y_sphere, radius_earth * z_sphere, 'FaceColor', 'b', 'EdgeColor', 'none');
surf(radius_moon * x_sphere + 1 - mu, radius_moon * y_sphere, radius_moon * z_sphere, ...
     'FaceColor', 'y', 'EdgeColor', 'none');
light('Position', [1 0 1], 'Style', 'infinite'); % ライトの位置とスタイルを設定
xlabel('x');
ylabel('y');
zlabel('z');
grid on;
axis equal;
view(3);


%% Equations of motion for the Circular Restricted Three-Body Problem
function dydt = cr3bp_ode(t, y, mu)
    % Extract positions and velocities
    x = y(1);
    y_pos = y(2);
    z = y(3);
    dx = y(4);
    dy = y(5);
    dz = y(6);
    
    % Distances to the primary bodies
    r1 = sqrt((x + mu)^2 + y_pos^2 + z^2);
    r2 = sqrt((x - 1 + mu)^2 + y_pos^2 + z^2);
    
    % Equations of motion
    ddx = 2*dy + x - (1 - mu)*(x + mu)/r1^3 - mu*(x - 1 + mu)/r2^3;
    ddy = -2*dx + y_pos - (1 - mu)*y_pos/r1^3 - mu*y_pos/r2^3;
    ddz = -(1 - mu)*z/r1^3 - mu*z/r2^3;
    
    % Return derivatives
    dydt = [dx; dy; dz; ddx; ddy; ddz];
end

以下の軌道が出てきます。

コードの解説

0. クリア

clear : MATLABに残っている変数をクリアします。
close all: 現在開いている図を閉じます。
大体この2つを書くことが多いです。

clear
close all

1. 定数の定義

地球月系のmass ratio = mass_moon / (mass_earth + mass_moon)
距離など
軌道伝播の初期値 y0 (x ,y ,z ,vx ,vy ,vz)

% Constants
mu = 0.01215058426994;  % Earth-Moon system mass ratio
earth_radius_km = 6371;  % Earth's radius in kilometers
moon_radius_km = 1737;   % Moon's radius in kilometer
distance_earth_moon_km = 384400;  % Average distance between Earth and Moon in kilometers

% Normalized radii
radius_earth = earth_radius_km / distance_earth_moon_km;
radius_moon = moon_radius_km / distance_earth_moon_km;

% Initial conditions
% これは、以下の尾崎さんのZennの記事の値を使用しています。
% https://zenn.dev/naoyaozaki/articles/a3c0b199cdf23f
y0_vec =[0.987384153663276, 0.0, 0.008372273063008, 0.0, 1.67419265037912, 0.0];

2. 軌道伝播の時間

軌道伝播は、[0 2]のように書くと、t=0→2 で積分される。これを軌道設計では「順伝播, forward propagation」という。
逆に、[0 -2]のように書くと、t=0→-2 のように積分される。これを軌道設計では、「逆伝播」backward propagationと呼ぶ。例えば、地球から月への遷移軌道を設計する際に、宇宙機は地球から月に向かうが、積分は逆方向に行うような設計手法があり、このときに用いる。

tspan = [0 2];% （時間は適当, 正規化されているので注意）

3. 微分方程式の積分、optionの定義

以下のように、@(変数)関数名（変数と定数）という書き方で運動方程式を呼び出す
- 今回は回転座標系なので月と地球は固定されていてtは使わないが、ここでtを呼び出すことで惑星が時変で動く方程式を書くことができる。
options　で、積分の精度などを指定できる。無くてもOK。※ない場合ばoptionsを消してください。

options = odeset('RelTol',1e-12,'AbsTol',1e-12);
[t, y] = ode45(@(t, y) cr3bp_ode(t, y, mu), tspan, y0_vec, options);

4. 軌道のプロット

軌道の描画　plot3
惑星の描画　surf (lightで影がつけれる）
3次元で見る view(3)

%% Plot the results
figure(1)
plot3(y(:,1), y(:,2), y(:,3), 'r', LineWidth=2);
hold on
[x_sphere, y_sphere, z_sphere] = sphere(50);
surf(radius_earth * x_sphere - mu, radius_earth * y_sphere, radius_earth * z_sphere, 'FaceColor', 'b', 'EdgeColor', 'none');
surf(radius_moon * x_sphere + 1 - mu, radius_moon * y_sphere, radius_moon * z_sphere, ...
     'FaceColor', 'y', 'EdgeColor', 'none');
light('Position', [1 0 1], 'Style', 'infinite'); % ライトの位置とスタイルを設定
xlabel('x');
ylabel('y');
zlabel('z');
grid on;
axis equal;
view(3);

5. 運動方程式の定義

回転座標系の正規化した地球月CR3BPは、こちらで導出を書いています。

y座標だけ、y_posになっていて汚いですがご容赦ください。x, zもx_pos, z_pox,
の意味です。
運動方程式なので、yの時間微分 dydt = [vx, vy, vz, ax, ay, az]が入ります。

function dydt = cr3bp_ode(t, y, mu)
    % Extract positions and velocities
    x = y(1);
    y_pos = y(2);
    z = y(3);
    dx = y(4);
    dy = y(5);
    dz = y(6);
    
    % Distances to the primary bodies
    r1 = sqrt((x + mu)^2 + y_pos^2 + z^2);
    r2 = sqrt((x - 1 + mu)^2 + y_pos^2 + z^2);
    
    % Equations of motion
    ddx = 2*dy + x - (1 - mu)*(x + mu)/r1^3 - mu*(x - 1 + mu)/r2^3;
    ddy = -2*dx + y_pos - (1 - mu)*y_pos/r1^3 - mu*y_pos/r2^3;
    ddz = -(1 - mu)*z/r1^3 - mu*z/r2^3;
    
    % Return derivatives
    dydt = [dx; dy; dz; ddx; ddy; ddz];
end

※流派によっては、軌道伝播ではなく軌道伝搬と書くこともあるが、論文内では統一したい ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

MATLABによる宇宙機の軌道伝播（地球-月 円制限三体問題におけるNRHOの描画）

要点