1. モチベーション
昨今、アルテミス計画をはじめとした月探査や、はやぶさ2、OSIRIS-REx、Psyche(1)などの小惑星探査、更には木星のトロイヤ群小惑星帯探査ミッションLucyなど、三体問題を考慮に入れた軌道設計が多くみられます。そこで、今回は三体問題の中でも基礎となる円制限三体問題(Circular Restricted Three Body Problem - CR3BP)をおさらいし、更にx-軸上のラグランジュ点(L1 ~ L3)状の周期解の一つであるハロー軌道の計算方法をまとめてみたいと思います。
2. 円制限三体問題(CR3BP)について
宇宙機の軌道設計における三体とは、二つの天体 ($m_1$, $m_2$) と宇宙機($m_3$)を考えます。尚、$m_1 > m_2 >>> m_3$と仮定することができるため、宇宙機の重力は天体の動きに影響を与えないものとします。
三体問題を考慮する際、基本的に $m_1$ と $m_2$ 重心を原点とし、$m_1$ から $m_2$ 向きのベクトルをx軸、$m_1$と$m_2$の回転軸をz軸とする回転座標系を用いります。(ので、自然と運動方程式も Hill's equations に似ていたりします。)さらに、数値計算を用意にするため、位置、速度、質量のスケーリングを合わせることができます。スケーリングする質量の合計 (Mass unit, $MU$) を $MU = m_1 + m_2$ と定義することで、これら天体の質量をそれぞれスケーリングすると
\begin{align}
\mu_1 &= \dfrac{m_1}{MU}
\\
\mu_2 &= \dfrac{m_2}{MU} = \mu
\end{align}
となります。三体問題の特徴を捉える値として、一般的に$\mu_2$は$\mu$と表し、運動方程式内でも使用します。ちなみに、$\mu_1 = 1-\mu$ となります。更に、距離のスケーリング (Distance unit, $DU$) を$m_1$と$m_2$の軌道長半径(semi-major axis)と定義すると、時間のスケーリング (Time unit $TU$) を
TU = \sqrt{ \dfrac{DU}{G(m_1 + m_2)} }
とすることで、$m_1$ と $m_2$ の周期運動を $2\pi$ と定義することができます。(CR3BPでは特に重要な意味を持たないものの、楕円制限三体問題や円制限四体問題などを考えるときはこの調整が役立つことになります。)
上記の回転座標機、スケーリングを踏まえ、CR3BPの運動方程式は次のようになります:
\begin{align}
\ddot{x} -2\dot{y}
&= x -\dfrac{1-\mu}{r_{1}^3} (x+\mu) - \dfrac{\mu}{r_{2}^3} \left(x-(1+\mu)\right)
\\
\ddot{y} +2\dot{x}
&= y -\dfrac{1-\mu}{r_{1}^3}y - \dfrac{\mu}{r_{2}^3}y
\\
\ddot{z}
&= -\dfrac{1-\mu}{r_{1}^3}z - \dfrac{\mu}{r_{2}^3}z
\end{align}
ここで $r_1$、$r_2$ はそれぞれ $m_3$ から $m_1$、$m_2$ までの距離になります。なお、ポテンシャル$U$を定義することで
U = \frac{x^{2}+y^{2}}{2} + \frac{1-\mu}{r_{1}} + \frac{\mu}{r_{2}}
$U$を踏まえると、運動方程式を以下のようにまとめることが出来ます(下付き文字はその状態に対する微分を表すものとします):
\begin{align}
\ddot{x} - 2\dot{y} &= U_x \\
\ddot{y} + 2\dot{x} &= U_y \\
\ddot{z} &= U_z
\end{align}
この運動方程式から唯一導出できる積分定数がヤコビ定数(Jacobi constant)です。このため、6つの軌道要素が求めらる二体問題($\ddot{\mathbf{r}} = -\dfrac{GM}{r^3}\mathbf{r}$)と違い、積分定数が一つしかない三体問題では一般解が求められません。静的解の一種であるラグランジュ点や、ハロー軌道を始めとした周期運動は、すべて数値解になります。
ちなみに、「円制限」の仮定を取り除くと、以下の制限三体問題(また三体問題にさらに天体の重力を一つ追加した四体問題)が導出できます:
- 楕円制限三体問題 (Elliptic restricted three body problem, ER3BP)
- 接円制限* 四体問題 (Bi-circular restricted four body problem, BCR4BP)
- 二重円制限* 四体問題 (Concentric circular restricted four body problem, CCR4BP)
(*四体問題については和訳が見つからなかったので、とりあえず名付けてあります…)
上記の三つに共通していることは、運動方程式が時間について変化する、という点にあります。
3. 初期予想解の生成と狙い撃ち法
数値解を求める際は、必ず初期予想解(initial guess)が必要になります。これが難しいところで、特に遷移軌道を計算するための初期予想解の生成は、解の最適化と同様に、重要な研究テーマでもあります。ここでは、古典的(?)なハロー軌道の初期予想解の生成法であるポアンカレ・リンステッド法 (Poincaré–Lindstedt method) を用いたアプローチを紹介します。
ハロー軌道の生成にあたって、軌道のxz-面に対する対称性を利用できます。この対称性により、xz-面にあるときハロー軌道の状態変数(positionとvelocity)は
\mathbf{x}_0 = \left[ x_0, 0, z_0, 0, \dot{y}_0, 0 \right]^T
となり、またちょうど半周期($P/2$)後も同じように
\mathbf{x}_{P/2} = \left[ x_{P/2}, 0, z_{P/2}, 0, \dot{y}_{P/2}, 0 \right]^T
という条件が成り立ちます。そこで、$\mathbf{x}_0$ の0でない項の初期予想が必要になります。そこで、文献 [3] の手法に沿って、求めるハロー軌道の周期$P$とz-方向の振幅 $A_Z$ をもとに、以下の式で求められます。
\begin{align}
x_0=& a_{21} A_{x}^{2}+a_{22} A_{z}^{2}-A_{x} \cos \phi+\left(a_{23} A_{x}^{2}-a_{24} A_{z}^{2}\right) \cos 2\phi +\left(a_{31} A_{x}^{3}-a_{32} A_{x} A_{z}^{2}\right) \cos 3 \phi
\\
z_0=& \delta_{n} A_{z} \cos \phi + \delta_{n} d_{21} A_{x} A_{z}\left(\cos 2\phi - 3\right) +\delta_{n}\left(d_{32} A_{z} A_{x}^{2}-d_{31} A_{z}^{3}\right) \cos 3 \phi
\\
\dot{y_0} =& k A_x \lambda \omega \cos{\phi}
+ \left(b_{21} A_{x}^{2}-b_{22} A_{z}^{2}\right) 2\lambda \omega \cos{2\phi}
+ \left(b_{31} A_{x}^{3}-b_{32} A_{x} A_{z}^{2}\right) 3\lambda \omega \cos{3\phi}
\end{align}
なお、上の式に出てくる変数の皆さん($a_{21}$だの$\delta_n$だの)はすべて文献 [3] の Appendix にあるものです(長いので割愛します)。
ただし、上記の値では、$P/2$後には正確にxz-面に戻らないため、剰余が存在します。
\mathbf{x}_{{P/2}_{ptrb}} = \left[ x_{P/2}, \Delta y_{P/2}, z_{P/2}, \Delta \dot{x}_{P/2}, \dot{y}_{P/2}, \Delta \dot{z}_{P/2} \right]^T
そこで、これらの余剰をresidualベクトル$F$、$P$を含める4つの自由変数のうち3つを$X$と定義します。例えば、ハロー軌道の$A_z$を固定したい場合、$x_{P/2}$, $\dot{y}_{P/2}$, $P$を$X$とし、
X =
\begin{bmatrix}
X_1 \\
\vdots \\
X_n
\end{bmatrix}
=
\begin{bmatrix}
x_{0} \\
\dot{y}_{0} \\
P/2
\end{bmatrix}
\quad \mathrm{and} \quad
F(X) =
\begin{bmatrix}
F_1(X) \\
\vdots \\
F_m(X)
\end{bmatrix}
=
\begin{bmatrix}
\Delta y_{P/2} \\
\Delta \dot{x}_{P/2} \\
\Delta \dot{z}_{P/2}
\end{bmatrix}
そこで、$F$をテイラー展開し、
F(X) \approx F(X_0) + DF(X_0) \cdot (X - X_0)
から
X^{j+1} = X^j - \left[ DF(X^j) \right]^{-1} F(X^j)
を反復することで$X$の数値解を得ることができます。なお、$DF$はヤコビ行列
DF(X_0) = \dfrac{\partial F}{\partial X}
= \begin{bmatrix}
\dfrac{\partial F_1}{\partial X_1} & \dots & \dfrac{\partial F_1}{\partial X_n} \\
\vdots & \ddots & \vdots \\
\dfrac{\partial F_m}{\partial X_1} & \dots & \dfrac{\partial F_m}{\partial X_n}
\end{bmatrix}
=
\begin{bmatrix}
\dfrac{\partial \Delta y_{P/2}}{\partial x_0} & \dfrac{\partial \Delta y_{P/2}}{\partial \dot{y}_0} & \dfrac{\partial \Delta y_{P/2}}{\partial t}
\\[0.8em]
\dfrac{\partial \Delta \dot{x}_{P/2}}{\partial x_0} & \dfrac{\partial \Delta \dot{x}_{P/2}}{\partial \dot{y}_0} & \dfrac{\partial \Delta \dot{x}_{P/2}}{\partial t}
\\[0.8em]
\dfrac{\partial \Delta \dot{z}_{P/2}}{\partial x_0} & \dfrac{\partial \Delta \dot{z}_{P/2}}{\partial \dot{y}_0} & \dfrac{\partial \Delta \dot{z}_{P/2}}{\partial t}
\end{bmatrix}
となります。$DF$のうち、状態に対する微分項は、運動方程式の状態遷移行列(state-transition matrix)$\Phi(t_i, t_0)$ より直接求められます。$\Phi$ は
\dot{\Phi}(t_i, t_j) = \left[
\begin{array}{c|c}
\mathbf{0}_{3,3} & \mathbf{I}_{3,3} \\
\hline
\mathbf{U}_{\mathbf{x} \mathbf{x}} & 2\mathbf{\Omega}
\end{array}
\right]
\Phi (t_i, t_j)
\quad \mathrm{where} \quad
\mathbf{U}_{\mathbf{x} \mathbf{x}}
= \begin{bmatrix}
U_{xx} & U_{xy} & U_{xz} \\
U_{yx} & U_{yy} & U_{yz} \\
U_{zx} & U_{zy} & U_{zz}
\end{bmatrix}
\quad \mathrm{and} \quad
\mathbf{\Omega} = \begin{bmatrix}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix}
に乗っ取ります。初期値 $\Phi(t_0, t_0)$ を単位行列とし、運動方程式と共に解くことができます。そうすることで、$DF$は以下のようにあらわすことが出来ます:
DF =
\begin{bmatrix}
\Phi_{2,1} & \Phi_{2,5} & \dot{y}_{T/2}
\\
\Phi_{4,1} & \Phi_{4,5} & \ddot{x}_{T/2}
\\
\Phi_{6,1} & \Phi_{6,5} & \ddot{z}_{T/2}
\end{bmatrix}
4. Pythonコード
以下のJupyter notebookにコード全文貼ってありますが、一部ここにのせておきます。
https://github.com/Yuricst/polaris/blob/main/examples/ex_ThreeBody.ipynb
上記notebookはターミナルよりgit clone https://github.com/Yuricst/polaris.gitでダウンロードできます。依存モジュールはnumba, numpy, pandas, scipyです。
# モジュールのインポート
import polaris.R3BP as r3bp
import polaris.Propagator as prop
# 地球-月の円制限三体問題を定義
param_earth_moon = r3bp.get_cr3bp_param('399','301') # NAIF ID's '399': Earth, '301': Moon
# ポアンカレ・リンステッド法による初期予想解の生成
haloinit = r3bp.get_halo_approx(mu=param_earth_moon.mu, lp=2, lstar=param_earth_moon.lstar, az_km=4000, family=1, phase=0.0)
# シューティング法による初期予想解の最適化
p_conv, state_conv, flag_conv = r3bp.ssdc_periodic_xzplane(param_earth_moon.mu, haloinit["state_guess"],
haloinit["period_guess"], fix="z", message=False)
# ハロー軌道を解く
prop0 = prop.propagate_cr3bp(param_earth_moon.mu, state_conv, p_conv)
# プロット
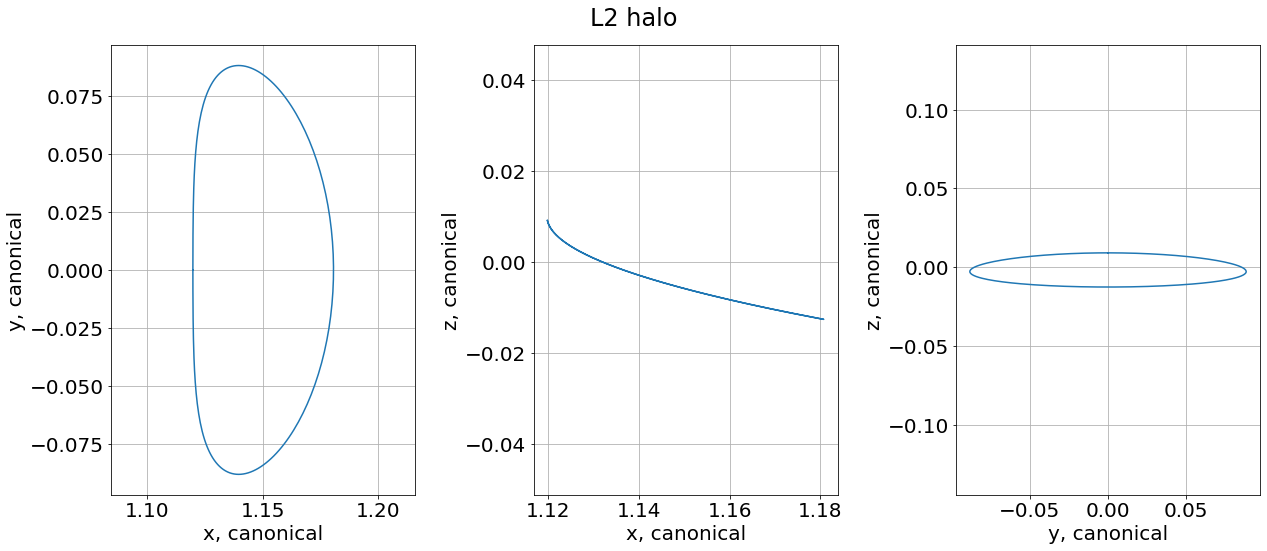
plt.rcParams["font.size"] = 20
fig, axs = plt.subplots(1, 3, figsize=(18, 8))
axs[0].plot(prop0["xs"], prop0["ys"])
axs[0].set(xlabel='x, canonical', ylabel='y, canonical')
axs[1].plot(prop0["xs"], prop0["zs"])
axs[1].set(xlabel='x, canonical', ylabel='z, canonical')
axs[2].plot(prop0["ys"], prop0["zs"])
axs[2].set(xlabel='y, canonical', ylabel='z, canonical')
for idx in range(3):
axs[idx].grid(True)
axs[idx].axis("equal")
plt.suptitle('L2 halo')
plt.tight_layout(rect=[0, 0.01, 1, 1.03])
plt.show()
なお、
-
r3bp.get_cr3bp_param()はhttps://github.com/Yuricst/polaris/blob/main/polaris/R3BP/_define_r3bp_param.py -
r3bp.get_halo_approx()はhttps://github.com/Yuricst/polaris/blob/main/polaris/R3BP/_approxHalo3rdOrder.py -
prop.propagate_cr3bp()はhttps://github.com/Yuricst/polaris/blob/main/polaris/Propagator/_propagator_cr3bp.py
で定義されています。
5. 参考
ウェブサイト
- JAXA Hayabusa2: https://www.hayabusa2.jaxa.jp/en/
- NASA Psyche: https://www.jpl.nasa.gov/missions/psyche/#:~:text=The%20Psyche%20mission%20is%20a,blocks%20of%20our%20solar%20system.
- NASA Lucy: https://www.nasa.gov/content/goddard/lucy-overview
文献
- Howell, "Three-Dimensional, Periodic, Halo Orbits", Celestial Mechanics, 1984
- D. Richardson, "Halo orbit formulation for the ISEE-3 mission", Journal of Guidance, Control, and Dynamics, 1980
- D. Richardson, "Analytical construction of periodic orbits about the collinear points", Celestial Mechanics, 1980
- Wang Sang Koon, "CS140B. Computation of Halo Orbit", http://www.cds.caltech.edu/archive/help/uploads/wiki/files/39/lecture_halo_2004.pdf