次元圧縮を片っ端から試してみた（t-SNE, PCA, MDS, UMAP） #Python

こんにちは。サーバもしっかり課金して書き始めたブログも三記事くらいで更新が止まった過去を持っている私ですが、Qiitaは不思議なことに続いています。

と思ったらこれが3記事目でしたね。これを最後に更新が途絶えたらつまりそういうことです。

最近は雑談の好きあらばQiita書いてますアピールをしている私なのですが、t-SNE（読み方がわからない方は過去の私の記事を参照してください）に付随してUMAPという次元圧縮手法の方がいいらしいよっていうことを教えていただいたので今日はそのネタでいきたいと思います。

先にお断りしておくと、結局どれがいいんだいっていう結論は出せなかったので、忙しい人は（後で読むにでも放り込んで）ブラウザバックしていただければと思います。

今回の流れ

今回使う手法の紹介
1. t-SNE
2. PCA
3. MDS
4. UMAP
ワインデータセットを使う
1. t-SNE
2. PCA
3. MDS
4. UMAP
手書き文字データセットを使う
1. t-SNE
2. PCA
3. MDS
4. UMAP
まとめ

かなり超大作になりそうな予感がしますね。

今回使う手法とコードの紹介

今回用いた手法を紹介します。それぞれの手法の詳しい説明はリンクを貼っておくので興味がある方は見てください。

今回はrandom_stateを変化させた時の挙動や実行時間などをもとに比較したかったのでrandom_stateを0~9で変化させて９枚のプロットを作り、実行時間に関しては9回の平均時間をもとに比較しております。

1. t-SNE

こちらは前回紹介しました。読み方はティースニーらしいです。仕組みについてはこれ以上のまとめはないと思いますので、リンクを貼ります。

t-SNEいいねえという感じでガチャガチャ使っていたのですが、指摘いただいてから色々調べてみると、ハイパーパラメーターの選択がかなり重要になってきたりするらしい。（下の記事参照）

また非線形な次元圧縮手法なので解釈が難しかったりします。

コードは以下の通り。

def plot_by_tsne(x, y):
    fig, axes = plt.subplots(3,3, sharex=True, sharey=True, figsize=(10,10))
    elapsed_time_list = []
    for random_state, ax in enumerate(axes.flatten()):
        start_time = time.time()
        model = TSNE(n_components=2, random_state=random_state)
        x_embedded = model.fit_transform(x)
        elapsed_time = time.time() - start_time
        elapsed_time_list.append(elapsed_time)
        ax.scatter(x_embedded[:, 0], x_embedded[:, 1], c=y, cmap=cm.tab10, alpha=0.5)
        ax.set_title("random_state={}".format(random_state))
    fig.tight_layout()
    print('tsne: {}s'.format(sum(elapsed_time_list)/len(elapsed_time_list)))
    plt.savefig('output/tsne.png')

2. PCA

続いてPCA（主成分分析）です。
データの分散がなるべく保存されるような特徴量を、元の特徴量の線形結合の形で導き次元圧縮をする手法です。
こちらは先ほどと異なり線形な次元圧縮方法で、各主成分を解釈することが容易で、またランダム性もなく一意に決まります。

ただ可視化した時にt-SNEほどは綺麗に分かれないことがほとんどというデメリットがあります。

コードは以下の通り。

def plot_by_pca(x, y):
    fig, axes = plt.subplots(3,3, sharex=True, sharey=True, figsize=(10,10))
    elapsed_time_list = []
    for random_state, ax in enumerate(axes.flatten()):
        start_time = time.time()
        model = PCA(n_components=2, random_state=random_state)
        x_embedded = model.fit_transform(x)
        elapsed_time = time.time() - start_time
        elapsed_time_list.append(elapsed_time)
        ax.scatter(x_embedded[:, 0], x_embedded[:, 1], c=y, cmap=cm.tab10, alpha=0.5)
        ax.set_title("random_state={}".format(random_state))
    fig.tight_layout()
    print('pca: {}s'.format(sum(elapsed_time_list)/len(elapsed_time_list)))
    plt.savefig('output/pca.png')

3. MDS

データ同士の距離を考え、その距離関係を低次元でできる限り反映できるような最適な配置を求め、次元圧縮していく方法です。

地図を使ってわかりやすく説明されている方がいらっしゃったのでリンクを貼っておきます。
こちらも非線形な次元圧縮法であるため解釈性は低いです。

コードは以下の通り。

def plot_by_mds(x, y):
    fig, axes = plt.subplots(3,3, sharex=True, sharey=True, figsize=(10,10))
    elapsed_time_list = []
    for random_state, ax in enumerate(axes.flatten()):
        start_time = time.time()
        model = MDS(n_components=2, random_state=random_state)
        x_embedded = model.fit_transform(x)
        elapsed_time = time.time() - start_time
        elapsed_time_list.append(elapsed_time)
        ax.scatter(x_embedded[:, 0], x_embedded[:, 1], c=y, cmap=cm.tab10, alpha=0.5)
        ax.set_title("random_state={}".format(random_state))
    fig.tight_layout()
    print('mds: {}s'.format(sum(elapsed_time_list)/len(elapsed_time_list)))
    plt.savefig('output/mds.png')

4. UMAP

最後がUMAPです。こちらがt-SNEより良さげなやつと言われていた手法です。

こちらをご覧ください。確かにt-SNEより良さげだということが書かれております。これは是非とも試してみたい。

さらには、先ほどt-SNEのとこで紹介した記事にも書かれていたのですが、t-SNEのプロットではクラスタのサイズ（密度的な意味）にはなんの意味もないかもしれないということでした。

その点を改善したものとして、densMAPたるものがあるらしく、それを使うとクラスタのサイズ（密度的な意味）も残したまま可視化することができます。詳しくは下記の記事を参照してください。

こちらのみdensmapパラメータを追加しております。コードは以下の通り。

def plot_by_umap(x, y, densmap=False):
    fig, axes = plt.subplots(3,3, sharex=True, sharey=True, figsize=(10,10))
    elapsed_time_list = []
    for random_state, ax in enumerate(axes.flatten()):
        start_time = time.time()
        model = UMAP(n_components=2, random_state=random_state, densmap=densmap)
        x_embedded = model.fit_transform(x)
        elapsed_time = time.time() - start_time
        elapsed_time_list.append(elapsed_time)
        ax.scatter(x_embedded[:, 0], x_embedded[:, 1], c=y, cmap=cm.tab10, alpha=0.5)
        ax.set_title("random_state={}".format(random_state))
    fig.tight_layout()
    print('umap: {}s'.format(sum(elapsed_time_list)/len(elapsed_time_list)))
    plt.savefig('output/umap.png')

ワインデータセットを二次元で可視化してみる

sklearnで用意されているデータセットを使ってみます。なぜワインにしたのかというと今禁酒しているからです。それ以外に意味はありません。

特徴量は13次元あるのでこいつを各種手法を用いて2次元に圧縮していきます。

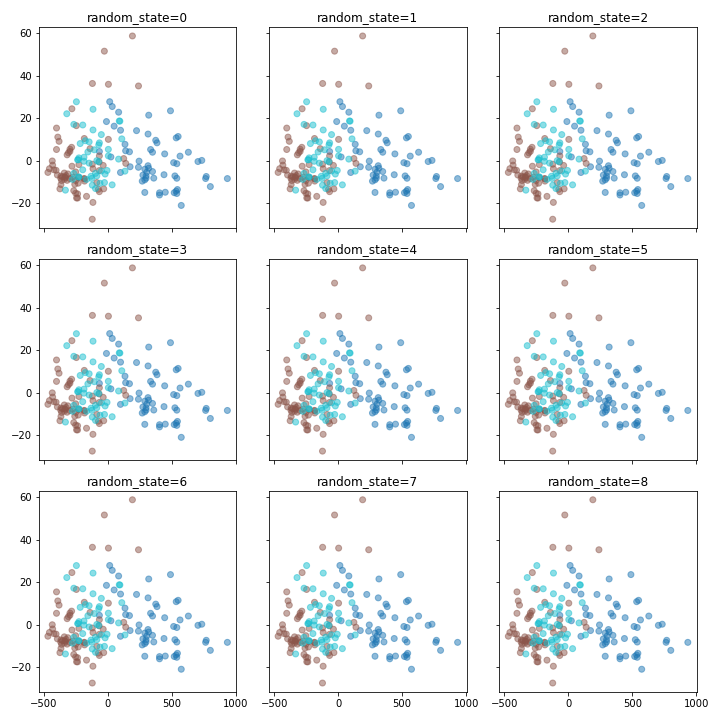
1. t-SNE

tsne: 0.621637847688463s

random_stateを変えながらプロットしてみたところ、向きの違いはあるものの全てが一列に並びました。3色に大まかにはわかれていますね。実行時間も平均で0.62秒といった感じです。
random_state=7とかほぼx軸だけで説明されてる感もあります。二次元にしてくれといったのに一次元に圧縮されたような気持ちになりますね。

2. PCA

pca: 0.002760940127902561s

PCAは先ほども説明したように線形の次元圧縮手法で一位に定まるため、random_stateを変えても同じプロットが並んでおります。実行時間も早いですね。なんとなくグラデーション感はありますが、綺麗に分かれているかというと微妙な印象です。

3. MDS

mds: 0.3778245713975694s

MDSもt-SNEと同じく一列に並んでおり、軸に並行にプロットされているものも複数見られます。t-SNEよりも潰れており、精度は悪い印象ですね。。

4. UMAP

umap: 0.730970541636149s

大本命のUMAPですがこちらはしっかりと与えられた次元の中で躍動している感じがあります。random_stateによって形状は異なっていますが、どれも二軸を活かしており、また分離もいい感じです。

しかし、早いと聞いていたのですが思ったよりも遅いですね。t-SNEよりも実行時間はかかるという結果になりました。

densmap

umap: 1.4377486175960965s

そしてdensmapの方も見てみましょう。先ほどのものと見比べてみると疎密がはっきりしている感じがします。正解ラベルごとに3種類の色分けをしておりますが、先ほどの可視化では浮かび上がってこなかったようなクラスタも見えてきており、正解ラベルの中でもさらに分類できるのかもしれないという気づきを与えてくれるような気がします。
実際にワインを飲みながら眺めてみたいですね。

手書き文字を二次元で可視化してみる

ワインデータセットでも十分面白かったのですが、t-SNEの方が早くなってしまうというUMAP的には面白くない結果になってしまいましたので、汚名返上すべくより高次元なデータでやってみたいと思います。
scikit-learnのdigit
(1797, 64)

特徴量は64次元あるのでこいつを各種手法を用いて2次元に圧縮していきます。

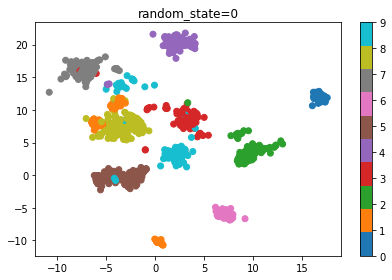
1. t-SNE

tsne: 4.200474977493286s

綺麗に分かれてくれていますね。random_stateを変えてもそこまで大きく精度が変わった印象はありません。

2. PCA

pca: 0.008606513341267904s

これだけ高次元になってデータ数も増えましたが安定の速さです。
ただ精度はというとうーん、かなり混じり気のあるプロットになっています。やはりこれだけ高次元のものを線型結合で二次元で表すのには限界があるようです。

いや逆にそれでこれだけ分かれていると考えるとすごいと褒めてあげるべきなのでしょうか。同じ図を９枚眺めながらいろんな感情が湧き上がってきました。

3. MDS

mds: 29.585671424865723s

t-SNEと比べると綺麗に分かれているとは言いづらいですが、犇き合うなかで大まかには分離できています。先ほどよりもいい結果を残してくれた気がします。PCAと似たテイストのプロットですが、PCAよりも精度はいい印象です。

ただ時間がかかりすぎです。また別の時に使います。今日のところは一旦ありがとうMDSという感じです。

4. UMAP

umap: 4.129069063398573s

さすがです。ほとんど混じり気なく二次元に圧縮できております。いいですね。

さてt-SNEよりも実行速度が速くなってほしくて行った手書き文字分類ですが、なんとか期待に応えてくれたようです。ほぼ一緒やんけ。
まあハナ差でも勝ちは勝ちです。

umap: 6.748186031977336s

そして実行時間は一枚あたり+2sくらいかかってはいますが、densmapも見てみましょう。こちらをみるとクラスタリングが若干ぼやけましたが、これが実情なのでしょう。

こちらをみると7と9、1と8が近かったりする様子が見て取れます。そして0や6などはかなり密度高く分離できているのですが、8とか5とか4とか7とかは割と密度が低くなっています。振れ幅が大きいのでしょうか。

終わりに

いろんな次元削減の方法があることがわかりました。速度や可視化の特性によって使い分けたいと思います。思ったよりもビミョい記事になったのは、この使い分けの仕方やそれぞれの手法のメリットデメリットをうまく自分の言葉で言語化できていないからですね。今後そこらへんを経験の中で学んでいきたいです。

そして今回はrandom_seedのみ設定してみましたが、それぞれの手法でさらに設定するパラメーターがあります。そこら辺は次回以降t-SNEやUMAPあたりから見ていこうと思います。

またPCAで低次元にした上で、t-SNEやUMAPにかけることで、高速・軽量化を図ると言うやり方もあるようです。

他にも次元圧縮の手法は発明されており、調べる中で出てきたPaCMAPとやらも良さげな匂いがするので使ってみようと考えています。

（追記）
この記事を書くきっかけになった方が教えてくださったこちらの動画を見ていたら、t-SNEはperplexityの設定で結構変わってくるようです。今度はここを変えてみようと思います。
https://youtu.be/ze08gwVPaXk?t=5124