本記事では、簡単な例を用いて固有値(eigenvalue)、**固有ベクトル(eigenvector)**の幾何的な意味を考えます。
固有値、固有ベクトルと言えば、理系の大学生なら4年間付き合うことになる概念なので、式だけでなく幾何的な意味も捉えておきましょう。
定義
はじめに固有値、固有ベクトルの定義を与えます。
$Definition.$ $n$次正方行列$A$に対して
$$
Ax=\lambda x
$$
を満たすベクトル$x\neq 0$が存在するとする。このとき、スカラー$\lambda$を$A$の固有値、$x$を固有値$\lambda$に対する$A$の固有ベクトルという。
例
まず、非常に簡単な例として、行列$A$を以下で与えます。
$$
A=
\begin{pmatrix}
2 & 0 \\
0 & 3
\end{pmatrix}
$$
これは、対角成分以外の要素が$0$であるような対角行列となっています。
では、この固有値と固有ベクトルを求めます。今回は固有値、固有ベクトルを求める部分がメインではないのでPythonでサクッと求めてしまいます。(もちろん定義に則って計算すれば同様の解が得られます。)
import numpy as np
A = np.array([[2,0],[0,3]])
eigval_A, eigvec_A = np.linalg.eig(A)
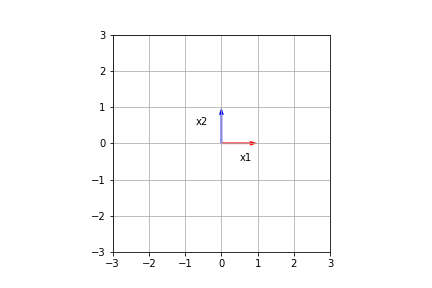
これより、行列$A$の固有値は、$\lambda_1 = 2, \lambda_2 = 3$となり、それぞれに対応する固有ベクトルは
$$
x_1 =
\begin{pmatrix}
1 \\
0
\end{pmatrix}, x_2 =
\begin{pmatrix}
0 \\
1
\end{pmatrix}
$$
となります。次の図が、固有ベクトルをあらわします。
幾何的意味(対角行列の場合)
ここからは、あるベクトル$v=(v_1, v_2)$に左から$A$をかけたときの線形写像を考えます。
今、$v=(1, 1)$というベクトルに左から$A$をかけると
$$
Av=
\begin{pmatrix}
2 & 0 \\
0 & 3
\end{pmatrix}
\begin{pmatrix}
1 \\
1
\end{pmatrix}=\begin{pmatrix}
2 \\
3
\end{pmatrix}
$$
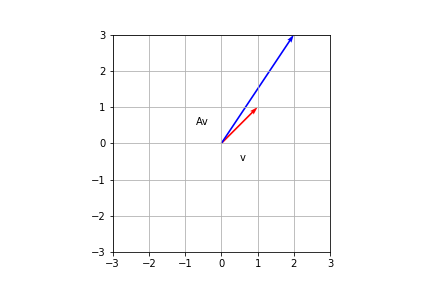
より、もとのベクトル$v$と写像後のベクトル$Av$は次のようにあらわされます。
これより、行列$A$をかけることによって$v$は$x$軸方向に$2$倍、$y$軸方向に$3$倍引き伸ばされたことがわかります。
このように、行列$A$によりもとのベクトルは、固有ベクトルの方向に固有値の大きさだけ引き伸ばされることがわかります。
任意のベクトル$v=(a,b)$($a,b$は任意のスカラー)に対して、これが成り立つことを確認します。まず、$Av$は
$$
Av=A\left( a\times
\begin{pmatrix}
1 \\
0
\end{pmatrix}+ b\times \begin{pmatrix}
0 \\
1
\end{pmatrix}\right)=a \times Ax_1 +b\times Ax_2
$$
とあらわされます。ここで、固有値、固有ベクトルの定義から$Ax_1 = \lambda_1 x_1$, $Ax_2 = \lambda_2 x_2$であるので
$$
Av= a \times \lambda_1 x_1 + b\times \lambda_2 x_2 = \begin{pmatrix}
2a \\
3b
\end{pmatrix}
$$
となることがわかります。これより、任意のベクトルに対しても同様のことが言えると確認できました。
幾何的意味(一般的な行列の場合)
上の例では、対角行列という特別な場合でしたので、対角成分=固有値となる簡単な例でしたが、実際はもう少し複雑です。
しかし、行列$A$の固有値が分かっている時にあるベクトル$v$を適当な固有ベクトル$(x_1, x_2)$の線形和であらわすことができれば、$Av$は簡単に計算することができます。すなわち、
$$v = \alpha x_1 + \beta x_2$$
であるとき、
$$Av = \alpha Ax_1 + \beta Ax_2 = \alpha \lambda_1 x_1 + \beta \lambda_2 x_2$$
となり、計算できることがわかります。また、式から行列計算を行わずに、$Av$の結果を求めることができたことも確認できます。
次に、対角成分が$0$でないような次の行列$B$を考えてみます。
$$
B=
\begin{pmatrix}
1 & 1 \\
-2 & 4
\end{pmatrix}
$$
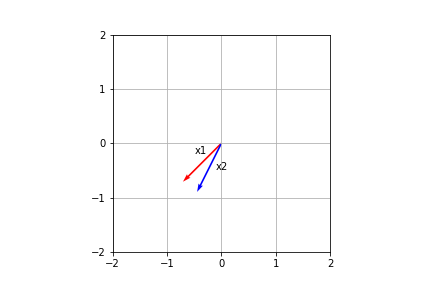
この固有値と固有ベクトルを求めると、固有値は$\lambda_1 = 2, \lambda_2 = 3$となり、固有ベクトルはそれぞれ
$$
x_1=\frac{1}{\sqrt{2}}
\begin{pmatrix}
-1 \\
-1
\end{pmatrix}, x_2 = \frac{1}{\sqrt{5}}
\begin{pmatrix}
-1 \\
-2
\end{pmatrix}
$$
となります。
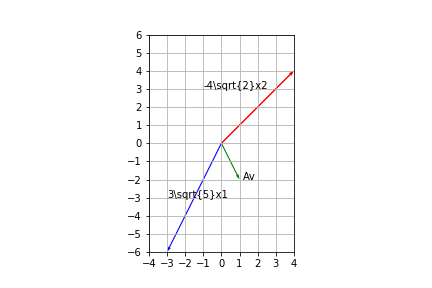
ここでベクトル$v$として$v=(1,0)$を考えると、このベクトルは
$$
v = -2\sqrt{2} x_1 + \sqrt{5} x_2
$$
とあらわされるので、
$$
Av = -2\sqrt{2} Ax_1 + \sqrt{5} Ax_2 = -4\sqrt{2} x_1 + 3\sqrt{5} x_2 = -4\begin{pmatrix}
-1 \\
-1
\end{pmatrix} + 3\begin{pmatrix}
-1 \\
-2
\end{pmatrix} = \begin{pmatrix}
1 \\
-2
\end{pmatrix}
$$
と計算できます。
おわりに
本記事では、簡単な例を通して固有値、固有ベクトルの幾何的な意味を見てきました。
前記事の主成分分析においても、固有値の大きさが寄与率に影響することに触れましたが、その意味が理解できたかと思います。
行列を扱う上で必ず出てくる固有値、固有ベクトルですが、その意味を考えれば、理解しやすいと思います。
何かあればコメントやツイッターでお気軽にお声がけください。