本記事では、多変量解析の代表的な手法の一つである**主成分分析(Principal Component Analysis; PCA)**について紹介します。
機械学習の文脈では、しばしば次元削減のために用いられますが、その他にもノイズの除去や多変量データの可視化などに用いられます。
本記事は大いに、以下の論文を参考にしています。詳細が知りたい方はそちらへ。
Hervé Abdi, Lynne J.Williams, "Principal Component Analysis", Available at [https://www.researchgate.net/profile/Lynne_Williams/publication/227644862_Principal_Component_Analysis/links/00b7d51657d5ad0d15000000/Principal-Component-Analysis.pdf], 2010.
概念
主成分分析の目的は、高次元のデータから分散が最大となる方向を求め、それをもとの次元と同じかそれ以下に射影することとなります。
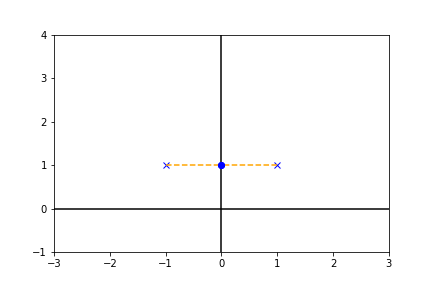
イメージを掴むため、2次元のデータを1次元へ次元削減する非常に簡単な例を挙げます。
今、二つの点
$$
(x,y)=(-1, 1), (1,1)
$$
があるとき、これをもとの点の情報を保ったまま1次元へ次元を減らすことを考えます。
図中での横方向の実線をx軸、縦方向の実線をy軸としたとき、まずy軸への射影を考えてみます。
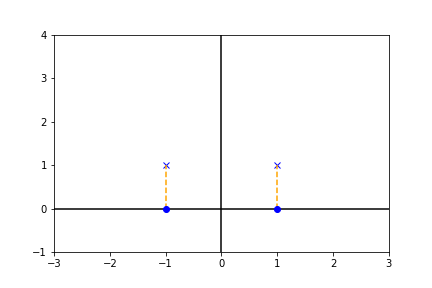
上図のように$(-1, 1)\mapsto (1)$, $(1, 1)\mapsto (1)$と二つの点が重なりもとの情報が失われてしまいます。
一方、x軸への射影を考えると、
上図より、$(-1, 1)\mapsto (-1)$, $(1, 1)\mapsto (1)$となり、もとのデータの情報を保ったまま、次元を削減することができます。このように高次元データから(例では2次元ですが)、分散が最大となる方向へ射影することにより次元を削減することができます。
実際には、例えば100次元から2次元へ次元削減を行ったとき、一般にもとのデータの情報を100%保持することはできません。しかし、どの程度それを保持できているか(寄与率)は求めることができます。
数学的解釈
以下では、主成分分析の数式的な解釈を与えます。
まず、$(n\times m)-$行列$X$において、${\rm rank}(X)=k$とします。
このとき、$X$は特異値分解を用いて、次のようにあらわされます。
$$X = P\Delta Q^T$$
ただし、$P$は$(n\times k)$の左特異値ベクトルを並べた行列、$Q$は$(m\times k)-$の右特異値ベクトルを並べた行列となります。また、$\Delta$は対角に特異値をもつ行列となります。ここで、$X^T X, XX^T$の非ゼロな(これらは半正定値行列なので正の)固有値を対角に並べた行列を$\Lambda$とすると、$\Delta ^2=\Lambda $となります。($\because XX^T = P \Delta Q^T Q \Delta P^T = P \Delta ^2 P^T $)
ここでは、特異値分解については詳しく触れないので、このような分解が存在するということを知っていただければ大丈夫です。
上式において、$F=P \Delta$(得点行列と呼ばれます)とあらわすと、以下の式が成り立ちます。
$$
F= P \Delta = P \Delta Q Q^T = XQ
$$
上式より、$Q$は 射影行列とみなすことができます。幾何的な解釈に関しては、先の論文内に例とともに挙げられています。
ここで、$F$は$(n\times k)$の得点行列でしたが、$l<k$を満たす$l$に対して、$(n\times l)$に次元削減された得点行列$F_l$を考えます。対応する射影行列を$Q_l$とすると、以下が成り立ちます。
$$
F_l = XQ_l
$$
このとき、射影行列$Q_l$、得点行列$F_l$を用いて求められる行列を$X_l$とすると
$$
\| X - X_l \| = \| FQ^T - F_l Q_l^T \|
$$
を最小化するような、階数$l$の行列を選ぶと良いことがわかります。ただし、行列$A$に対して、$\| A \|$はフロベニウスノルムをあらわします。
これを求めると、寄与の大きい$l$個の特異値に対応する特異ベクトルが射影行列として残ります。(よく見る寄与が大きい順=固有値が大きい順にベクトルを選択するという結果との関連もわかると思います)
最後に、射影後の寄与率について少し触れます。
上記の括弧書きで書いたように、特徴量の分散共分散行列の固有値が大きいものから寄与が大きいという情報を目にしたことがあるかもしれません。
分散共分散行列を$\sum$とすると、その固有値$\lambda$、固有ベクトル$v$は以下の式を満たします。
$$
\sum v= \lambda v
$$
ここで、データに含まれる多くの情報(分散)を含む固有ベクトルを選びますが、固有値は固有ベクトルの大きさをあらわすため、固有値が大きい順にそれに対応する軸を選びます。
ここで、固有値$\lambda_i$の寄与率は、以下の式であらわされます。
$$
\frac{\lambda_i}{\sum_{i} \lambda_i}
$$
例として、固有値が$\lambda = 3,2,1$のとき、3次元から2次元への次元削減は
$$
\frac{3+2}{3+2+1} = 0.83333...
$$
より、83%程度の情報を保持します。
おわりに
本記事では、特異値分解を用いて主成分分析と紐づけてきました。
最後に少しだけ書きましたが、分散共分散行列との関係性も非常に興味深いものなのでぜひ調べて見てください。
何かあればコメントやツイッターでお気軽にお声がけください。