LoginSignup
70
92

More than 5 years have passed since last update.

@hitomatagi

OpenCV3とPython3で形状のある物体の輪郭と方向を認識する（主成分分析：PCA、固有ベクトル）

Last updated at Posted at 2016-08-24

主成分分析（PCA: Principal Component Analysis）とは

　物には様々な特徴量があり、その特徴量で物の種類を特定できることがあります。
　例えば、コーヒーであれば、酸味、苦味、煎り、コク、色、香りといった特徴量があり、その組み合わせで、コーヒーの種類（モカ、キリマンジャロ、マンデリン、etc.）を特定することができたりします。ただ、特徴量のほうも様々あり、種類を特定するにあたり、特徴として有効なものとあまり有効ではないものがでてきます。例えば、コーヒーの特徴量として重さや硬さなども考えれますが、こちらは種類を特定するためにはあまり役立ちそうにもありません。価格は特徴量として少しは役立つかもしれません。

　主成分分析（PCA）とは、対象物を特定するにあたり、強く特徴を表している成分を、標準偏差、共分散行列、固有ベクトルなどを使って特定していく分析方法になります。また、関係の深い特徴量に注目することで、データの次元圧縮を行うことができ、計算量の削減、データ量/メモリ量の削減に効果を発揮します。

　OpenCVも、主成分分析（PCA）をcoreモジュールでサポートしています。今回は、形状のある物体の方向をOpenCVの主成分分析（PCA）を取り扱うメソッドを使って計算し、輪郭と主成分の方向を矢印で表示すプログラムを作成してみます。最終的には、以下の図のようになります。

pca_output.png
　　　　　　　物体の輪郭（赤）と主成分ベクトル（水色）を表示

OpenCV

OpenCV(Open Source Computer Vision Library)はBSDライセンスの映像/画像処理ライブラリ集です。画像のフィルタ処理、テンプレートマッチング、物体認識、映像解析、機械学習などのアルゴリズムが多数用意されています。

■ OpenCVを使った動体追跡の例 (OpenCV Google Summer of Code 2015)
https://www.youtube.com/watch?v=OUbUFn71S4s

■ インストールと簡単な使い方はこちら
OpenCV 3（core + contrib）をPython 3の環境にインストール＆OpenCV 2とOpenCV 3の違い＆簡単な動作チェック

■ 静止画像の処理についてはこちら
OpenCVでエッジ検出してみる
OpenCVで各種フィルター処理をする（グラディエント、ハイパス、ラプラシアン、ガウシアン）
OpenCVで特徴点を抽出する（AgastFeature, FAST, GFTT, MSER, AKAZE, BRISK, KAZE, ORB, SimpleBlob）
OpenCVを使った顔認識（Haar-like特徴分類器）
OpenCVを使って誰の顔なのかを推定する（Eigenface, Fisherface, LBPH）

■ 動画の処理についてはこちら
OpenCVで動画をリアルタイムに変換してみる
OpenCVでWebカメラ/ビデオカメラの動画をリアルタイムに変換してみる
OpenCVでオプティカルフローをリアルタイムに描画する（Shi-Tomasi法、Lucas-Kanade法）
OpenCVを使った物体追跡（マウスで指定した特徴点をLucas-Kanade法で追跡する
OpenCVを使ったモーション テンプレート解析（リアルタイムに物体とその動く方向を認識する）

アルゴリズム

　通常、主成分分析というと、下記のような散布図の点について分析を行うのをよく見かけるのではないでしょうか。プロットは、元々多次元だった特徴量を２次元に次元圧縮したものです。さらに矢印はプロットに対する第一主成分と第二主成分のベクトルを表しています。
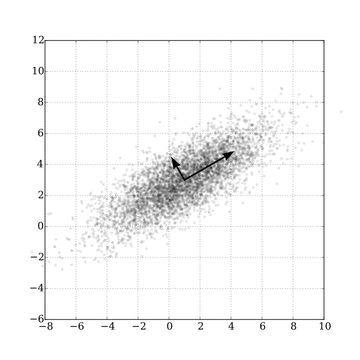
GaussianScatterPCA.svg.png
　　　　　　　　　　出典：Wikipedia - 主成分分析

　図形の主成分分析も、この応用で行うことができます。
　手順としては以下のようになります。

  1. 物体の方向を認識するために不要と思われるカラー情報を白黒情報に変換します。
  2. 物体の輪郭を２次元（x座標、y座標）の点として認識します。
  3. 輪郭の点（x, y）の集まりに対して主成分分析（ＰＣＡ）します。
  4. 主成分方向のベクトル（固有ベクトル）を求め画像に描画します。
  5. 各物体に対して１～４を繰り返します。
  • コーヒーの例では、コクや苦味が特徴量でしたが、画像では、x座標、y座標が特徴量になります。
  • ステップ１では、ＲＧＢのカラー情報を白黒情報に変換しています。ＰＣＡ分析ではありませんが、これも次元圧縮の一種です。
  • ステップ２がそれなりに大変そうですが、こちらに関しては、OpenCVのcv2.findContours()メソッドが、輪郭の座標を物体ごとに計算してくれます。
  • ステップ３に関しては、OpenCVのcv2.PCACompute()メソッドで平均値と固有ベクトル（主成分方向のベクトル）を求めることができます。
  • ステップ４に関しては、OpenCVのcv2.line()メソッドで固有ベクトル方向に線を描画します。

　ということで、OpenCVを使えばメソッドをいくつか呼び出すだけで、物体の輪郭と方向を認識することができてしまいます。

プログラム

  • 実行環境
    • Python: ver.3.5.2
    • OpenCV: ver.3.1.0
  • サンプル画像
    • OpenCVのパッケージに付属している画像（pca_test1.jpg）を利用
      [OpenCV Install Dir]/samples/data/pca_test1.jpg

  • プログラムの注意点

    • 描画系はintで処理する

    • 分析系はfloatで処理する
      配列の中身がintのままPCACompute()メソッドを実行すると以下のエラーがでます。

      error: (-210) Unsupported combination of input and output array formats in function cv::reduce

    • 主成分は１次元のみ取得（maxComponents=1）するように指示した

    • 輪郭の座標を主成分分析に用いるため、中間点のデータも取得するように指示した（cv2.CHAIN_APPROX_NONE）

    • 通常、主成分分析をする場合は、前処理としてデータの標準化をします。今回の画像処理は、２次元のx座標とy座標で、それぞれに対する重みづけに違いがないため、データ標準化の前処理を行っていません。

pca.py
# -*- coding: utf-8 -*-
import cv2
import math
import numpy as np


# ベクトルを描画する
def drawAxis(img, start_pt, vec, colour, length):
    # アンチエイリアス
    CV_AA = 16

    # 終了点
    end_pt = (int(start_pt[0] + length * vec[0]), int(start_pt[1] + length * vec[1]))

    # 中心を描画
    cv2.circle(img, (int(start_pt[0]), int(start_pt[1])), 5, colour, 1)

    # 軸線を描画
    cv2.line(img, (int(start_pt[0]), int(start_pt[1])), end_pt, colour, 1, CV_AA);

    # 先端の矢印を描画
    angle = math.atan2(vec[1], vec[0])
    print(angle)

    qx0 = int(end_pt[0] - 9 * math.cos(angle + math.pi / 4));
    qy0 = int(end_pt[1] - 9 * math.sin(angle + math.pi / 4));
    cv2.line(img, end_pt, (qx0, qy0), colour, 1, CV_AA);

    qx1 = int(end_pt[0] - 9 * math.cos(angle - math.pi / 4));
    qy1 = int(end_pt[1] - 9 * math.sin(angle - math.pi / 4));
    cv2.line(img, end_pt, (qx1, qy1), colour, 1, CV_AA);


if __name__ == '__main__':
    # 画像を読み込む
    src = cv2.imread("pca_test1.jpg")

    # グレースケールに変換
    gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)

    # ２値化
    retval, bw = cv2.threshold(gray, 50, 255, cv2.THRESH_BINARY | cv2.THRESH_OTSU)

    # 輪郭を抽出
    #   contours : [領域][Point No][0][x=0, y=1]
    #   cv2.CHAIN_APPROX_NONE: 中間点も保持する
    #   cv2.CHAIN_APPROX_SIMPLE: 中間点は保持しない
    img, contours, hierarchy = cv2.findContours(bw, cv2.RETR_LIST, cv2.CHAIN_APPROX_NONE)

    # 各輪郭に対する処理
    for i in range(0, len(contours)):

        # 輪郭の領域を計算
        area = cv2.contourArea(contours[i])

        # ノイズ（小さすぎる領域）と全体の輪郭（大きすぎる領域）を除外
        if area < 1e2 or 1e5 < area:
            continue

        # 輪郭を描画する
        cv2.drawContours(src, contours, i, (0, 0, 255), 2, 8, hierarchy, 0)

        # 輪郭データを浮動小数点型の配列に格納
        X = np.array(contours[i], dtype=np.float).reshape((contours[i].shape[0], contours[i].shape[2]))

        # PCA（１次元）
        mean, eigenvectors = cv2.PCACompute(X, mean=np.array([], dtype=np.float), maxComponents=1)

        # 主成分方向のベクトルを描画
        pt = (mean[0][0], mean[0][1])
        vec = (eigenvectors[0][0], eigenvectors[0][1])
        drawAxis(src, pt, vec, (255, 255, 0), 150)


    # 表示
    cv2.imshow('output', src)
    cv2.waitKey(0)

    # 終了処理
    cv2.destroyAllWindows()

実行結果は、最初に示した画像のようになります。

おまけ

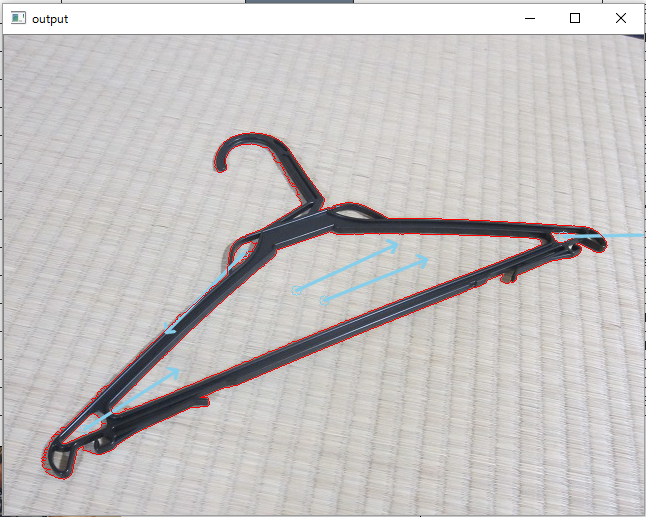
　サンプル画像だけではなく、他の画像についても輪郭と方向を認識させてみましょう。
　例えば、畳のようなパターン模様の上に穴が特徴的なハンガーを置いて分析してみます。
　結果は、小さな穴を囲む輪郭３か所、外側の輪郭と内側の輪郭２か所について、主成分方向のベクトルを表示させることができました。
hanger_out.png

70
92
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
70
92