はじめに
こんにちは。ディープラーニングを1から実装している物好き、映画好きです。
今は死ぬほどわかりやすい解説書もあるし、ブラウザからクライアント完結で実行できるJS実装サイトもあるし、論文も多いので勉強資料には事欠きませんが、
いざ実装となると、解説書でスルーされている部分があったり、理論とは無関係な設計上の問題が浮上したりして、なかなか「さらっと実装」とは行きません(でした)。
※ソースや数式詳細は全部こちらに置いています。現状純粋groovyなので死ぬほど遅く、また一部性能向上のためのアルゴリズムが未実装です。例えばMNIST(unitテスト化しています)で95-97%くらいの正答率です。勉強用なので。。。すみません。
もとよりディープラーニングは単一のモジュールやアルゴリズムではなく、複数モジュールや複数テクニックの総称なので、そのうちの何かでつまづくと学習も実装もストップし、気分的に前に進めなくなってしまいます。
また基本レベルがいい加減だと応用レベルでそのしっぺ返しがきます(きました)。
(例)バックプロパゲーションの数式だけ追って納得してパーセプトロンを実装してみて、
「割と簡単かも」と思っていると(思っていました)・・・
- 畳込みネットワークの局所コントラスト正規化層でのバックプロパ―ゲーションを自力で立式できない
- 全結合層、シグモイド層、ソフトマックス層などを独立モジュールとする層分離方式を実装できない
※この例をみて、そんなの簡単だと思った方は読む必要はありません。
時間を無駄にせず、映画館でもTSUTAYAでもどこでも行ってください。
結局のところ、困ったときは、自分で考えて立式していくしかありません。
このシリーズでは、ポイントと思ったことを書いていこうと思います。
(ふりかえると今回は基本の復習で終わってしまいました、すみません)
バックプロパゲーションの復習
※手書きですみません
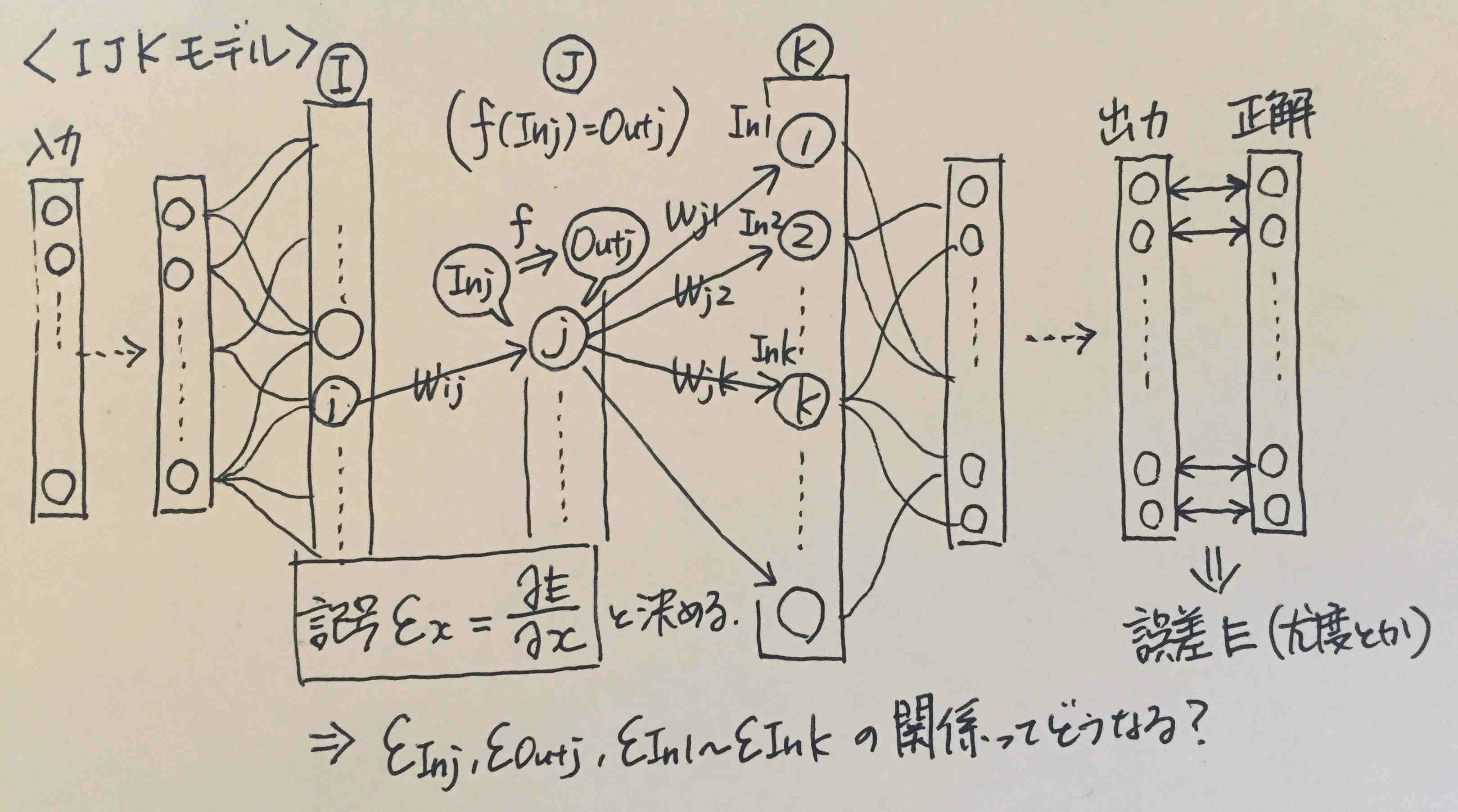
<ユニット間の入出力の関係>(出力値と線形結合する重みを有するネットワーク限定)
ある層のあるユニットは、前の層Iの**1つ以上の(※)**ユニットと結合していて、各出力を重みづけしたものの合計値を受け取る。図で言えば、
In_j = \sum_{i} Out_i * W_{ij}\\
In_k = \sum_{j} Out_j * W_{jk}
※1つの場合(層分離方式でのシグモイド層)も、全部の場合(全結合層)も、一部の場合(畳み込み層)もあります。いずれの場合も、つながっている分だけで考えて行けば良いんだ、ということです。これは後で出てくる他の$\sum$達にも言えることです。
ただ「重み」という話で言えば、局所コントラスト正規化層やソフトマックス層などは、上記のような単純な形にはなりません。
<ユニットの入出力の関係>
入力と出力の間には関数で定義される関係があるとします。つまり、
f(In_j) = Out_j
神経学的には発火/活性化と呼ばれる作用です。
シグモイド関数(ロジスティック関数)などが用いられますが、それは発火させたい場合にはそう設定すると学習効率が良かったり計算しやすかったり(導関数の形に依存)するからそうしているだけです。
定義上活性化がない($f(x) = x$)場合や活性化してもあまり意味がないという場合もあります。とにかく関数の関係になっている、とだけ定義して中身を気にせず一般化していける、というのがポイントです。
<とにかく目的は誤差を最小化すること>
出力値(出力ユニットの各値)と正解信号の比較から、誤差Eを定義&計算します。その誤差が小さくなるように、層間パラメータ$\theta$(図の場合は重み)を調整していくこと=学習です。
ソフトマックス層など出力が確率値になる場合は、正解信号を出力する尤度Lを用いて、
E = - \ln{L(\theta)}
と定義します(この形を負の対数尤度といいます)。このようにする理由も一応確認しておきます。
- 「負」にする理由:
尤度の最大化=誤差の最小化になるので、一律に「誤差の最小化」というくくりで扱えるためです。扱えると何が嬉しいかといえば、もちろん実装の設計で嬉しいのです。誤差の正体が負の対数尤度であろうと最小二乗誤差であろうと、それは出力層クラスだけが知っていれば良いことであって、上位クラスは「出力層が提出してきた誤差っていう値が小さくなっていけば学習成功だぜ」と思っていれば良いのです - 対数にする理由:
尤度は確率積の形になることが多く、そのまま計算すると桁溢れで計算精度の問題が出てくるらしいです。対数にすると、積を和の形に変換でき、その問題が解決されます。また、確率値が指数を含む関数になる場合は、指数の対数=>相殺になって簡単な形に変形できたりするし、微分も楽になります。
最小化する=>勾配降下法ということになるのですが、もし「誤差の最小化」というくくりで扱う必要がないのなら、素直に「尤度の最大化」をすれば良く、その場合は勾配上昇法になります(ボルツマンマシン単体の解説書で、実際にそうしているのを見ました)。名前と符号が変わるだけでやることは同じです。
<バタフライ効果とバックプロパゲーション>
誤差$E$を最小化するために重み$W_{ij}$を調整するには、勾配降下法が使えます。
そのためには、$\frac{\partial E}{\partial W_{ij}}$がわかれば良い、ということになります。
誤差とは結局、出力層と教師信号の間で計算されるものです。
勾配$\frac{\partial E}{\partial W_{ij}}$とは、$W_{ij}$をちょっと変えると$E$がどのくらい変わるか、という変化度合い(影響度合い)です。
ちょっと妄想します。
「$W_{ij}$をちょっと変えると、$In_j$がちょっと変わり、$Out_j$がちょっと変わり、$In_1$,$In_2$,・・・,$In_k$,...がちょっと変わり、その影響は後のニューロンすべてに影響を及ぼし、もしかすると出力値に至っては、もうその影響は「ちょっと」どころじゃないかもしれない、そして蝶が嵐を起こし、アシュトン・カッチャーが目覚めると○○○が大変なことになっているかもしれない」
ということです(『バタフライ・エフェクト』は超傑作スリラーなので、こんな記事読む暇があったらすぐ観てください。教授や上司に怒られたらディープラーニングの勉強だと言えば大丈夫です。怖いのが苦手で涙腺崩壊系が好きな人には『アバウト・タイム』がおススメです)。
影響の大小はともかく、大事なのは、$W_{ij}$がちょっと変わると、その影響はユニットjからたどれる全てのユニットに影響を与え、最終的に出力値に影響する、ということです。
バックプロパゲーションとは、バタフライ効果を未来から過去(結果から原因)に遡る形で、(誤差を少なくするような)良い影響を与えるような重みの変化を逆算しよう、という話です。
アシュトン・カッチャーは望ましい現実を得るために何度も過去に戻らないといけません。ただし、戻る度に着実に現実が改善していっている、とはとても言えませんでした。
慌てて場当たり的な対処を繰り返していた、つまり確率的勾配降下法で単一データに対する誤差だけを改善していて、さらに重みの更新量が激しすぎたのだと思います。
もっと全体への影響をみてバッチ法やミニバッチ法を使い、さらに正則化を取り入れて慎重に重みを更新していれば、あんな怖いことにはならなかったはずです。
すみません。
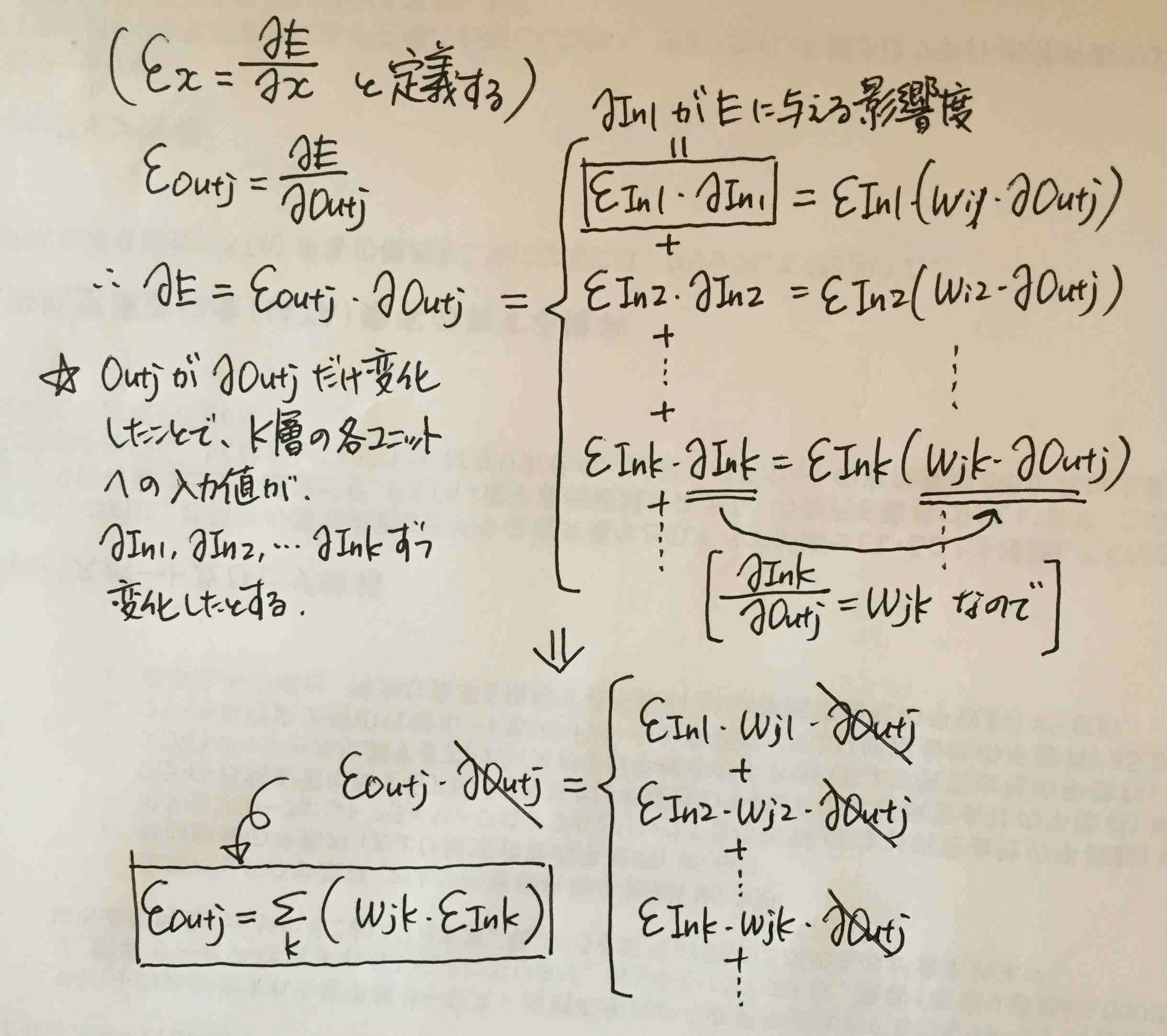
「変化の影響が伝わっていく」というのを数式で考えるということは、重み勾配$\frac{\partial E}{\partial W_{ij}}$ではなく、入力値や出力値の勾配、$\frac{\partial E}{\partial In_j}$,$\frac{\partial E}{\partial Out_j}$,$\frac{\partial E}{\partial In_k}$などの関係を考えるということです。
「ちょっとずつ変わっていく」ものは重みではなく、入力値や出力値だからです。
※資源を節約していてすみません。
勾配の記号として$\varepsilon$(イプシロン)を導入しています。解説書によっては、$\delta$(デルタ)と表記されることも多く、「デルタの逆伝播が~」みたいな使われ方を見たりします。
上記のようにして、
\varepsilon_{Outj} = \sum_{k} (W_{jk} * \varepsilon_{In_k})
ということがわかりました(よく解説書では「微分連鎖により~」の一言で上記の式を導出していますが、丁寧に書いてみました)。これが逆伝播(backward)の式の一種です。
ところで、もうすでにバックプロパゲーションの形、後のユニットの勾配に重みをかけた和を取ると、前のユニットの勾配が計算できる、という形になっています。
ちょっと脱線しますが、ここで$J$層から$K$層へのデータの流れ、つまり**順伝播(forward)**を思い出してみます。
In_k = \sum_{j} (W_{jk} * Out_j)
backwardとforwardの式を比べるとどうでしょうか?
$j$と$k$が交替し、$in$と$out$の関係が交替し、データと勾配$\varepsilon$が交替した、美しい対称形をしていると思います(僕だけかも?)。
層分離方式になるとユニット内の活性化がなくなって、$In_j = Out_j$、$\varepsilon_{In_j} = \varepsilon_{Out_j}$となるので、$in$と$out$の区別のない、より綺麗な対称形になります。
こういう事も実装で役立つかもしれません(自分は式ではわかっていましたが実装で改めて対称性を意識しました)。
おそらく頭の良い人は、
「グラフの形と微分連鎖から、対称式になるのは見た瞬間にわかりますよね?どちらも重みの積和だから、データベクトル/勾配ベクトルと重み行列の行列計算に帰着することもわかってますよね? え、行列計算じゃなく各ニューロンをオブジェクトにしてるんですか? は? ニューロンの気持ちになりたい? 馬鹿じゃないの」
と冷めた口調で言うことでしょう。経験上こういう人は頭が良すぎて映画の世界に入り込めないタイプです。
脱線終わり。
重み$W_{ij}$が直接影響を及ぼすのは、$Out_j$ではなく$In_j$なので、$\varepsilon_{Inj}$がどう計算できるかも調べます。
そもそも、$f(In_j) = Out_j$という単純な関係だったので、$\varepsilon_{In_j}$と$\varepsilon_{Out_j}$も単純な関係のはずです。
まず合成関数の微分公式より、
\frac{\partial E}{\partial In_j} = \frac{\partial E}{\partial Out_j} \cdot \frac{\partial Out_j}{\partial In_j}
となり、記号変換すると、$\frac{\partial E}{\partial In_j} = \varepsilon_{In_j}$、$\frac{\partial E}{\partial Out_j} = \varepsilon_{Out_j}$、$\frac{\partial Out_j}{\partial In_j} = f'(In_j)$なので、
\varepsilon_{In_j} = \varepsilon_{Out_j} \cdot f'(In_j)
です。これを、$\varepsilon_{Out_j}$を消去する形でbackwardの式に代入すると、
\varepsilon_{In_j} = f'(In_j) \cdot \sum_{k} (W_{jk} * \varepsilon_{In_k})
となります。ユニット入力値の勾配$\varepsilon_{In_x}$同士の関係式になりました。
つまり、ドミノ方式でポンポン計算していけるということです。
最期に、$\varepsilon_{In_j}$と$\frac{\partial E}{\partial W_{ij}}$の関係がわかれば終わりです。
またまた合成関数の微分公式より、
\frac{\partial E}{\partial W_{ij}} = \frac{\partial E}{\partial In_j} \cdot \frac{\partial In_j}{\partial W_{ij}}
ここで、$\frac{\partial E}{\partial In_j} = \varepsilon_{In_j}$、$\frac{\partial In_j}{\partial W_{ij}} = Out_i$(これは最初の式、$In_j = \sum_{i} Out_i * W_{ij}$から)なので、
\frac{\partial E}{\partial W_{ij}} = \varepsilon_{In_j} \cdot Out_i
教科書的まとめと設計の関係
図に示したような全結合層でのバックプロパゲーションの手順はこうなります。
- $\varepsilon_{In_j} = f'(In_j) \cdot \sum_{k} (W_{jk} * \varepsilon_{k})$によって、すべてのユニットの$\varepsilon$を求める。はじめの一歩、つまり出力層のユニットの$\varepsilon$達は、出力データと教師信号に基づいて、出力層のアルゴリズムが責任をもって計算する
- 求めた$\varepsilon$を使って、$\frac{\partial E}{\partial W_{ij}} = \varepsilon_{In_j} \cdot Out_i$の式により、 更新したい重み$W_{ij}$について$\frac{\partial E}{\partial W_{ij}}$を求める
- 勾配降下法によって重み$W_{ij}$を更新する
これを実装の観点で書き直すとこうなります。
- forward:
入力層から出力層に向かって順伝播計算を行い、各ニューロンの入出力値を確定させ、それを保存しておく(重み更新で入力値を使うから)。計算の無駄を避けるため、他にもbackwardや重み更新で役立つものはここで取っておく。 - backward:
出力層から入力層に向かって逆伝播計算(εの更新)を行う。先回り計算方式では各ユニットにおいて、そのεと(1で保存しておいた)入力値を使って、重み勾配を計算して保存しておく。本質的には勾配の計算は3に回しても別に構いません。重み更新量の決定には、重み勾配だけでなく、学習率の減衰率、各種正則化パラメータ、モメンタムなど、学習反復数に依存する変数が関わってくるので、先回り計算してしまうかどうかは設計方針によって変わると思います。 - 重み更新:
2で保存した重み勾配を使って重みを更新する。これは各リンク(重みが載っているユニット間のつながり)ごとに、その入力値とεから計算するだけなので、forwardやbackwardみたいな計算の方向性はありません。適当にリンクを選んでその重みだけ更新しても別に支障はありません。 - 学習終了条件に達するまで、1~3を反復
基本的なことですが、backwardの中で重み更新をやってしまってはいけません。
やっていいのは、重み更新の準備のための重み勾配の計算までです。
backwardのεの更新式には重みが登場しますが、この更新式は、「順伝播が終わって誤差が確定した状態のネットワーク」を前提として導出した式だったはずです。もしbackwardの途中である重みを更新してしまうと、その重みを使うεの更新式では「あれ?想定した重みの値じゃなくなってる!」となって話の前提が狂います。
ポイント
上記ではまとめとして、
\varepsilon_{In_j} = f'(In_j) \cdot \sum_{k} (W_{jk} * \varepsilon_{In_k})
を提示しました。あえてこれを融通の利かない式と呼んでおきます。
というのも、これをみて「ふんふん」と納得して素直に実装すると、全結合層専用の設計になる危険があるからです。もしこの式を暗記して試験に行ったとすると、多層パーセプトロンの問題は完璧に解けても、その他のディープラーニングの問題では対処できない気がします。
もし新たな種類の層が出てきたとき、そこに「これがデルタの更新式です」という式が明示されていなかったらどうするのでしょうか(もちろん明示されていたとしても、自分で咀嚼納得する必要があるので、明示されていない場合とそう変わりません)。
言われたことは完璧にできるけど、ちょっとした変化球にも対応できないようなエンジニアにはなりたくありません。
ディープラーニングには全結合層以外にも多様なネットワークが登場します。そのたびに別個に式を組み、別個に実装していくと、DRYにできず吐き気がして死にたくなったり、教科書の式通りに作って予想通りに動いてそれで自分は楽しいんだろうか皆はライブラリで楽しく遊んでいるのに・・・と空しくなったりする可能性があります。
また、共通の構造を明確にすることで、異なる見た目に見えるネットワークが実は数学的にはほとんど同じ処理になっている事に気づく場合があります。これは実装に直結します。
式に戻って、ポイントを書きます。
(1) 多様な層に共通する数学的性質を記述した式にする
メリット:
- 突然変異みたいな恐ろしい見た目のヤツら(局所コントラスト正規化層や階層的ソフトマックス層)が出てきても、その層の場合の式を立てられる
- 「共通する数学的性質」は、実装上も抽象クラスのメソッドとしてそのまま実装できたり、設計の役に立つ
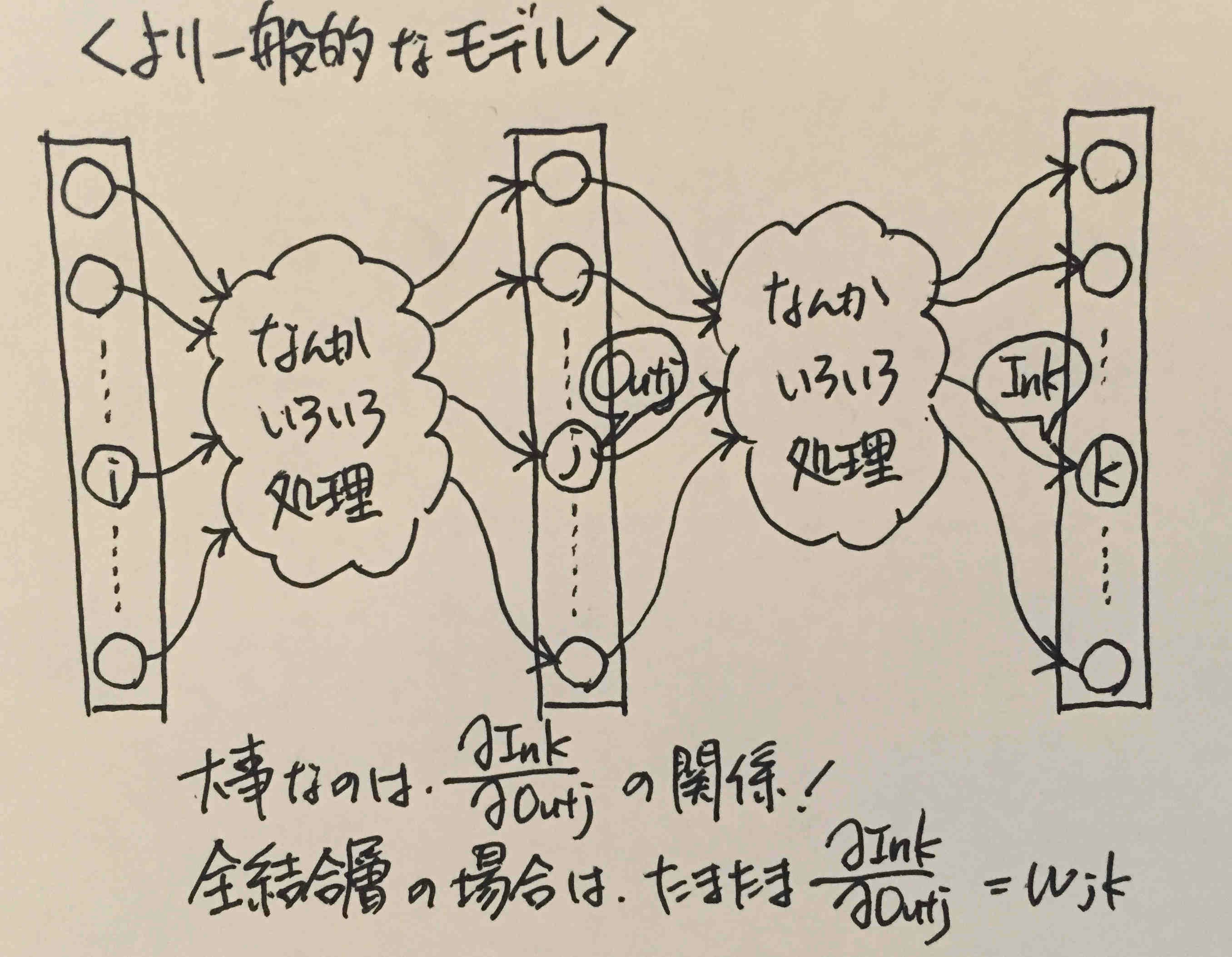
上記の式で言えば、「全結合層」専用になる原因は、$W_{jk}$の部分です。
これがどこから出てきたのかというと、手書きの汚らしい図の中の$\frac{\partial In_k}{\partial Out_j} = W_{jk}$という部分です。これは全結合層だからたまたまそうなっているだけ、です。
もっとふわっとした一般的ネットワークを考えると、
※他人へのメッセージで「!」を多用する人は軽薄で信用できないか表現の語彙が乏しい人なので話さないようにしているのですが、自分用メモでの「!」は許されます。
という感じです。
「なんかいろいろ処理」の中身が、全結合層のように線形結合だとは限りません。
しかしその中身が何であるとしても、
\varepsilon_{In_j} = f'(In_j) \cdot \sum_{k} (\frac{\partial In_k}{\partial Out_j} * \varepsilon_{k})
の関係は成立します。あと既に書いたように、$f(In_j)$の中身もここでは気にしていません。
層間の処理がどんなものであっても、活性化関数の中身が何であっても、この式の関係は一般性を失わないということです。これを念頭におけば、新しい層を学習/実装するときでも、パニックにならずに(なりました)その層でのバックプロパゲーションの式を算出できます。
(2)複数ステップを含む場合、小ステップに分解できるなら分解する
また上記の式は、$f'(In_j)$と$\sum_{k} (W_{jk} * \varepsilon_{k})$の積の形になっています。
なぜこの形になったのかを考えてみると、
$f'(In_j)$はユニット内での活性化に由来し、$\sum_{k} (W_{jk} * \varepsilon_{k})$は線形結合に由来します。図で考えても、なんとなくこの2つは分けて考えることができそうで、それは最小モジュール化・DRY化にもつながってきそうです。
これはディープラーニングライブラリで主流となっている層分離方式(勝手に命名)の設計につながります。本当は今回それをまとめるつもりでしたが、好きな映画の話をして満足してしまったので、次回「細胞膜とミルフィーユ」に回します。