この記事はAteam Hikkoshi Samurai Inc. & Ateam Connect Inc.(エイチーム引越し侍、エイチームコネクト) Advent Calendar 2019 6日目の記事です。
はじめに
AI やら機械学習やらディープラーニングやらの言葉を聞かない日はないくらいに当たり前の技術になってきていますが、個人的にはだいぶ前に Python で TensorFlow をちょっといじったくらいで止まっていました。
いいかげんちゃんと学習しますか、ということで、改めて始めることに。
で、まず言語は何を使おうかと考えたんですが、また Python に戻るのもおもしろくないし、NumPy があるとはいえ、やっぱり業務で本格的に使うには実行速度がネックになるんじゃないかと思っているし、かといって、20年前の学生時代に使っていた C/C++ や Java を使うのもおもしろくないし、頻繁にトライ&エラーを繰り返すにあたってコンパイルもめんどくさいし…
そんななか、動的言語にも関わらず、JITコンパイラで実行速度が速い! Matlab 風の数式表現が使えて数式が自然にかける!という触れ込みの Julia に出会いました。
2012年産まれと新しい言語だけど、最近は人気も良い意味で落ち着いてきたようだし、メジャーバージョンも 1 になって1年以上がたち安定してそうなのでいよいよ触ってみることに。
いろいろと衝撃を受けたので、興味深い言語仕様をメモ書きしてみました。
(今回は機械学習の話はありません)
準備
Juliaマニュアル v1.3
日本語マニュアル v1.0
https://julialang.org/downloads/
からダウンロードして、インストールして julia で REPL が起動
以降、すべて REPL 内での実行です。
数式、変数名の特徴
まずは最初の衝撃はこれ。
数値と変数の掛け算は「*」を省略できる。
2 * x は 2x と書ける。
そして関数定義
f(x) = x^2 + 3x + 4
まんま数式。まんま。
もちろん、普通に
function f(x, y)
x + y
end
とも書ける。return 文がなくても最後の文の値が暗黙的に返戻される。
数式として一般的に用いられている文字(ascii じゃない unicode な文字)も使える。
円周率や自然対数の底は、π、e として定義済みだし、α、λ とかの文字を変数として使える。
x₀, x₁ なんて変数名も使える。あぁ初期値なんだろうな、って見てすぐに分かる。REPL上での入力はそれぞれ x\_0[tab], x\_1[tab]
プライム「′」を関数名に使って
f′(x) = 2x + 3
って命名してあげれば即座に f(x) の導関数だなってのが見て分かる。
これだけで機械学習に使う言語として優秀だとゆっていいレベル。
(Julia が自動で微分してくれるわけじゃないけど)
REPL上では \prime[tab] で入力できる。
ちなみにシングルクォート「'」じゃないよ。シングルクォートは文字リテラルに使うから変数名には使えない。
REPL上でのその他の [Unicode な文字の入力一覧]
(https://docs.julialang.org/en/v1.3/manual/unicode-input/index.html)
ちなみに、複素数もそのまま普通に計算できる。虚数単位は im
julia> (1+2im) * (2+3im)
-4 + 7im
i じゃないんかーいと思ったけど、Julia は * を省略できるので、一般的なインデックスの変数名の i や j を虚数単位としてしまうと、Python(虚数単位は j)での表現のような 2j が 2*j との区別がつかないので im にしたのは致し方ないと思う…
こんな感じで数式をだいぶそのままプログラムコードとして記述できるのが心地よい。
パフォーマンス上の注意点
せっかく実行速度のために Julia を選んだのだから、性能をきちんと出すための注意点をメモ。
行列のメモリ配置
Juliaは行列のメモリ配置が列方向優先になっているため、列方向に処理をしたほうが効率がよい。
# 列方向
function sumbycol(x)
s = 0.0
for j in 1:size(x, 2)
for i in 1:size(x, 1)
s += x[i, j]
end
end
s
end
# 行方向
function sumbyrow(x)
s = 0.0
for i in 1:size(x, 1)
for j in 1:size(x, 2)
s += x[i, j]
end
end
s
end
ここで、size(配列, i)は、配列において、i 次元(?)の数を返す。
行列においては、size(行列,1) は列数を、size(行列,2) は行数を返す。(あ、行列って言い方と逆だな)
上記のように、例えば全要素をループで回して足し算する場合であれば、列方向は行方向に比べて数倍速かった。
そんなん一緖やんっていいたくなるけど、キャッシュの問題、、、か…
julia> using BenchmarkTools
julia> x = rand(10^4, 10^4);
julia> @btime sumbycol(x2)
100.933 ms (1 allocation: 16 bytes)
5.0003068365876675e7
julia> @btime sumbyrow(x2)
740.561 ms (1 allocation: 16 bytes)
5.0003068365882814e7
型安定性
性能のため 型安定 を意識する。
JITコンパイラが型を迷わないように確定的にしてあげる。途中で型を変えない。
浮動小数点が入るかもしれない変数を 0 で初期化して Int にしてしまったり、
x = ifelse(y > 0, y, 0) のように x に代入するのが typeof(y) なのか 0(Int)なのか分からなくしてしまうことがないように
x = ifelse(y > 0, y, zero(x)) と書いてあげる。
型がコーディング時に決まってる必要はないけど、
同じ型が分かる(暗黙の型変換をしなくてよい)ようにしておくと JIT コンパイラに優しくなる。つまり速くなる。
マニュアルのパフォーマンスの項目に、ダメな例として書かれていたもの。
function foo1(n)
s = 1
for i in 1:n
s /= rand()
end
return s
end
何気なく 1 で初期化しちゃってるので、s は Int になっちゃうけど、その後、浮動小数点の割り算が入るので型が変更されて Float に。
function foo2(n)
s = 1.0
for i in 1:n
s /= rand()
end
return s
end
ちゃんと最初から Float として初期化してあげる。
Test モジュールの @inferred マクロで型推測がうまく行っているかどうかをチェックできる。
julia> using Test
julia> @inferred foo1(100)
ERROR: return type Float64 does not match inferred return type Union{Float64, Int64}
Stacktrace:
[1] error(::String) at ./error.jl:33
[2] top-level scope at REPL[20]:1
foo1() は返戻値の型が Float64 と Int64(引数が 0 の時は返戻値が 1 なので) の Union になっちゃって、実際には Float64 が返ってきたからかエラーになっている。
julia> @inferred foo2(100)
8.190153651053117e51
foo2() はエラーなし。
つぎに BenchmarkTools モジュールでパフォーマンスをみてみる。
julia> using BenchmarkTools
julia> @benchmark foo1(100)
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 628.482 ns (0.00% GC)
median time: 633.171 ns (0.00% GC)
mean time: 655.641 ns (0.00% GC)
maximum time: 2.250 μs (0.00% GC)
--------------
samples: 10000
evals/sample: 170
julia> @benchmark foo2(100)
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 591.670 ns (0.00% GC)
median time: 596.888 ns (0.00% GC)
mean time: 614.801 ns (0.00% GC)
maximum time: 1.808 μs (0.00% GC)
--------------
samples: 10000
evals/sample: 179
もっと気楽に @time マクロでさくっと実行時間を見るのもアリ。
julia> @time [foo1(100) for i in 1:100_000];
0.091100 seconds (74.54 k allocations: 4.655 MiB)
julia> @time [foo2(100) for i in 1:100_000];
0.085508 seconds (66.72 k allocations: 4.219 MiB, 5.16% gc time)
マニュアルのパフォーマンスチップスにも、他の本にもこれで速くなるって書いてあったけど、最近のバージョンは JITコンパイラが優秀なのかそこまでは変化がない。
そこで別のケースで、型が不安定になるのでパフォーマンスの問題があるとマニュアルに書いてあるクロージャでも試してみた。
function bar1(a::Float64)
x = a
return function in()
x += rand()
return x
end
end
f1 = bar1(1.0)
仮引数にも型を指定して、その後も推定ができなくなる箇所はなさそうだけど、
julia> @inferred f1()
ERROR: return type Float64 does not match inferred return type Any
Stacktrace:
[1] error(::String) at ./error.jl:33
[2] top-level scope at REPL[35]:1
怒られた。
さらに詳しく見るために、@code_warntype マクロを使う。
Qiita の julia ハイライトだと分かりにくかったので画像で。
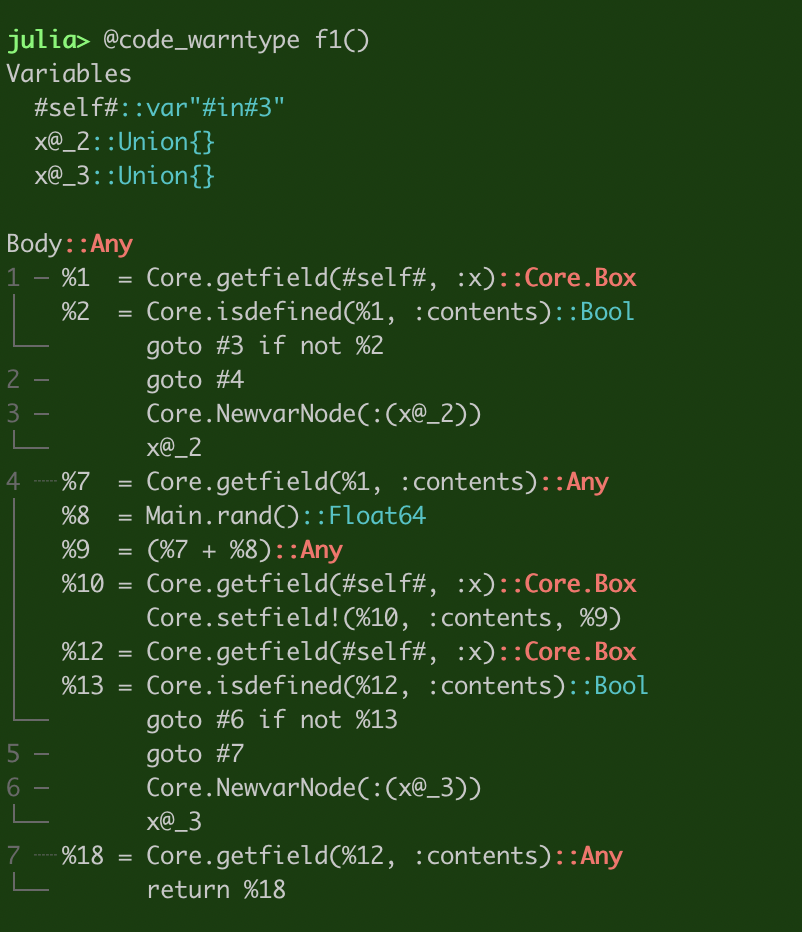
赤字になってる Core.Box や Any のところがあかんっぽい。型が決められてない。
いちおうベンチマークを見ておく。
julia> @benchmark f1()
BenchmarkTools.Trial:
memory estimate: 32 bytes
allocs estimate: 2
--------------
minimum time: 37.759 ns (0.00% GC)
median time: 38.623 ns (0.00% GC)
mean time: 41.275 ns (0.66% GC)
maximum time: 548.599 ns (91.18% GC)
--------------
julia> @time [f1() for _= 1:100_000]
0.042589 seconds (261.78 k allocations: 7.037 MiB)
内部関数内において x の型が分からなくなっちゃってるようなので、アノテーションしてあげる。
function bar2(a::Float64)
x = a
return function in()
x′ = x::Float64
x′ += rand()
x = x′
return x′
end
end
f2 = bar2(1.0)
@code_warntype で見てみる。
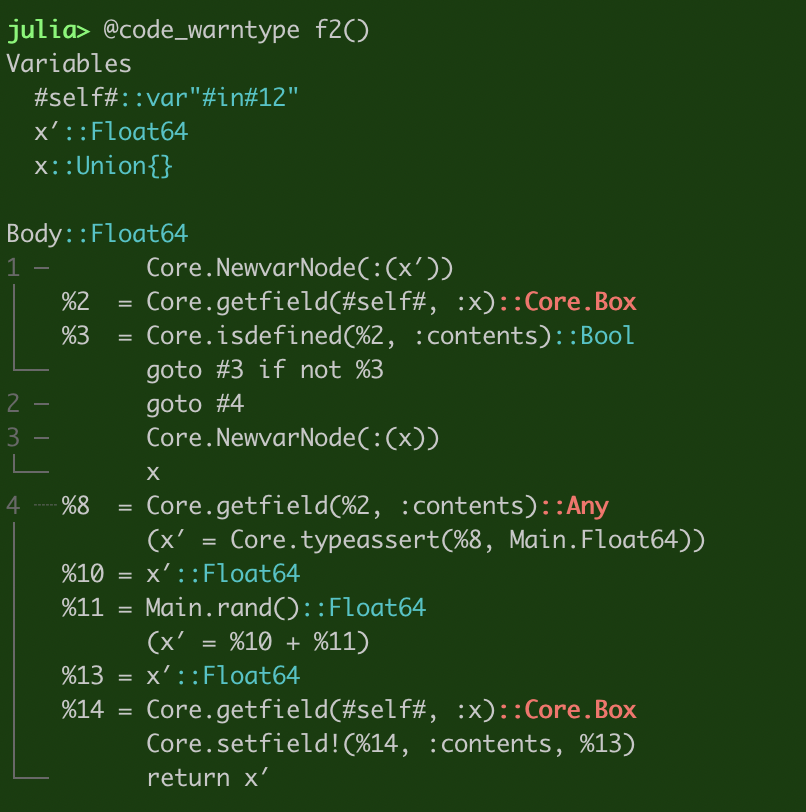
型不明の x に2回アクセスせざるを得ないので完全にはクリーンにはなってないが、Core.Box と Any が減った。
@inferred のエラーもなくなった。
julia> @inferred f2()
1.320610151967484
ベンチを取ってみると、
julia> @benchmark f2()
BenchmarkTools.Trial:
memory estimate: 32 bytes
allocs estimate: 2
--------------
minimum time: 28.974 ns (0.00% GC)
median time: 31.039 ns (0.00% GC)
mean time: 32.889 ns (1.33% GC)
maximum time: 779.424 ns (95.96% GC)
--------------
julia> @time [f2() for _=1:100_000]
0.039468 seconds (252.53 k allocations: 6.520 MiB)
3割くらい速くなった感じかな。
@inferred, @code_warntype でダメそうなところを発見して、修正して、
@benchmark、@btime、@time でチェックしていく感じですね。
ループ内での if 文
ループ内で if 文で分岐すると最適化できないので、ifelse() を使う。
アセンブリコードで分岐命令が吐かれなくなり、代わりに両方のケースの計算が行われるらしい。
両方の計算が軽ければこっちの方が良い
function loop1(x)
s = 0.0
for e in x
if e > 0
s += e
end
end
return s
end
julia> x = randn(100_000);
julia> @time loop1(x)
0.009386 seconds (11.09 k allocations: 521.271 KiB)
39696.262433922166
julia> @benchmark loop1(x)
BenchmarkTools.Trial:
memory estimate: 16 bytes
allocs estimate: 1
--------------
minimum time: 143.752 μs (0.00% GC)
median time: 143.808 μs (0.00% GC)
mean time: 147.395 μs (0.00% GC)
maximum time: 373.223 μs (0.00% GC)
--------------
条件分岐を ifelse() で書き換えてみる。
function loop2(x)
s = 0.0
for e in x
s += ifelse(e > 0, e, 0.0)
end
return s
end
julia> @benchmark loop2(x)
BenchmarkTools.Trial:
memory estimate: 16 bytes
allocs estimate: 1
--------------
minimum time: 97.853 μs (0.00% GC)
median time: 97.873 μs (0.00% GC)
mean time: 101.369 μs (0.00% GC)
maximum time: 407.765 μs (0.00% GC)
3分の2くらいの実行時間になりました!
長くなってきたので、この辺で…
他にもパフォーマンスTipsはいろいろありますが、コンパイラを意識しながらコードを書くのは久々なので楽しみながら学んでいきます!
それでは! Let's enjoy Julia!
お知らせ
エイチームグループでは一緒に活躍してくれる優秀な人材を募集中です。
興味のある方はぜひともエイチームグループ採用ページよりご応募ください!
Qiita Jobsのエイチーム引越し侍社内システム企画 / 開発チーム、社内システム開発エンジニアを募集!からチャットでご質問いただくことも可能です!
明日
明日はスーパー新卒1年目の @hinora くんの記事です! お楽しみに!