はじめに

この記事は Ateam LifeDesign Advent Calendar 2023 の 5日目の記事です。

昨年のアドカレの記事に引き続き、Tableau で何かやろうと考えていたところ、社内から「去年のクリスマスツリーを3D化しろ」という無茶振りが聞こえてきたのですが、それは聞かなかったことにしつつ、そういえば Tableau って3Dを描画する機能ってないよな、と思い、やってみることにしました。

三次元の棒グラフとか円グラフのことではなくて、三次元の座標を Tableau 上で表現する方法です。

まずは Excel でやってみる

Excel だと「等高線」を使うことで簡単に 3D で描画できます。

例えば、以下のスクショのように、2次元のガウス関数を描画する場合、

1行目に X軸として -2〜2 の範囲で 0.1 刻みで値を入れ、
A列に Y軸として同じく -2 〜 2 の範囲で 0.1 刻みで値を入れ、
Z軸の値として、B2セルに =EXP(-(B$1^2 + $A2^2)) と入れる。
それを B2:AP42のセルにコピー。

つまり、
$z = f(x,y) = e^{-(x^2+y^2)}$
という形のグラフ。

A1:AP42 を選択して、「挿入」→「グラフ」で「等高線」を選択すると、上に貼り付けたスクショのように（メキシカンハットのような）図が現れます。

この形を Tableau で実現することを目指してみる。

Tableau 用にデータを準備

Excel だと座標データを行-列の形で持ったけど、Tableau だと扱いにくいので、
x, y, z の3列のデータにしたい。

Excel で作ろうとしたら案外うまく作れなかったので、python でちょちょいと。
z は Tableau の計算フィールドで作れば良いから、(x,y)の組だけ。
ちなみにこのコードは ChatGPT4 にお願いして書いてもらったもの。

values = [i * 0.1 for i in range(-20,21)]
output_lines = [f"{x:.1f}, {y:.1f}" for x in values for y in values]
formatted_output = "\n".join(output_lines)
print(formatted_output)

出力されたCSVファイル

data.csv

-2.0, -2.0
-2.0, -1.9
-2.0, -1.8
-2.0, -1.7
・・・
2.0, 1.6
2.0, 1.7
2.0, 1.8
2.0, 1.9
2.0, 2.0

これを Tableau でテキストファイルとして読み込む。

フィールド名は x, y にしておく。

z は描画したい関数で計算フィールドを作成する。
今回は EXP(-SQUARE([x])-SQUARE([y]))*3 としてみたが、他にも色々試してみるとおもしろい。

SQRT(8 - SQUARE([x]) - SQUARE([y]))     // 楕円面
SQRT(SQUARE([x]) + SQUARE([y]))       // 一葉双曲面
SQRT(2*SQUARE([x]) - 1.5*SQUARE([y])) // 二葉双曲面

（ただし、これらは本来は z = ±√ だが + しか考慮してない）

Tableau で描画できるように 2次元の座標に落とし込む

xyzの3次元の座標を、Tableau で描画できるように平面に投影する。
投影の考え方は個人的にはこちらの資料が分かりやすかったです。（以下の説明はこの資料とは軸の向きが異なるので符号等は一致しません）

Tableau 上の縦軸、横軸をそれぞれ v,h とし x,y,z軸が下図のようにあるとすると、

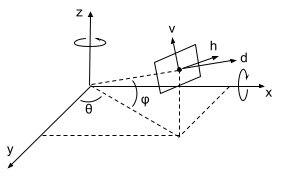
z軸周りに θ だけ回転させる
x軸周りに φ だけ回転させる

これで y軸方向が視点方向(d軸)と一致するので、
奥行方向を無視して縦横(v,h)だけで表現できる。

ちなみに、奥行方向は d として計算はしておく。

1. z軸周りに θ だけ回転させる

xy平面における回転写像は以下の式になるので、

\begin{pmatrix}
x' \\
y'
\end{pmatrix}
 = 
\begin{pmatrix}
cosθ & -sinθ \\
sinθ & cosθ \\
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}

Tableau の計算フィールドでは下記のようになる。

x' = [x]*COS(RADIANS(θ)) - [y]*SIN(RADIANS(θ))
y' = [x]*SIN(RADIANS(θ)) + [y]*COS(RADIANS(θ))
z' = [z]

2. x軸周りに φ だけ回転させる

z軸の時と同様に

x'' = [x']
y'' = [y']*COS(RADIANS(φ)) - [z']*SIN(RADIANS(φ))
z'' = [y']*SIN(RADIANS(φ)) + [z']*COS(RADIANS(φ))

これで、h-v平面と一致するので、

h = [x'']
v = [z'']

となる。
ちなみに奥行き d は

d = [y'']

となる。

これらを計算フィールドとして作成。
θ、φ をパラメーターとして作成。

h を列に、v を行に入れる。
（h,v はメジャーなため、デフォルトだと合計が計算されて一つのプロットになってしまうので、「合計(ｈ)」「合計(v)」となっているのをそれぞれディメンションに変更する）

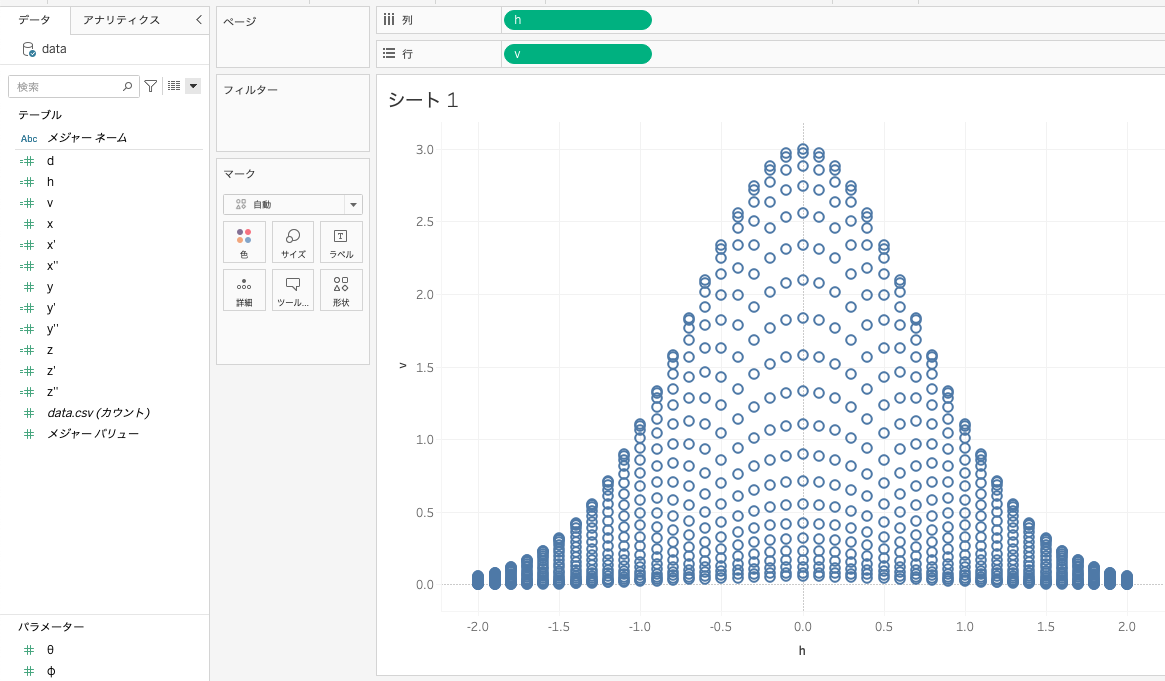
奥行方面がつぶれた平面に投影された図形になる。（θ、φの初期値を0としている）
ここからθ、φの角度を変化させることで斜めから見ているようにする。

見た目の調整

θ、φ のパラメーターを、-180 〜 180 の範囲にして、適当なステップサイズ（例えば 5）を定義し、表示させる
縦軸横軸を -4〜4 くらいで固定し、ヘッダーを非表示とする
高さが分かりやすいように z を「色」に入れ、「温度の分化」でステップドカラーにして等高線っぽくする
d を「サイズ」に入れ、奥に行くほどサイズを小さくする。（手前がマイナスになってしまっていたので d = -[y''] とした）

（一旦）完成

（集合体恐怖症の方ごめんなさい）
θ、φ のスライドをいじることで、上下左右にぐりぐり（とはいきませんが）動かせます。
動かすことで立体がよりイメージしやすくなります。

やりたいけどやれてないこと

プロットの描画で手前を優先する
点ではなく面になるようにプロット円のサイズを大きくして塗りつぶすと、プロットの順番の問題（？）で常に下側から覗いているような感じになってしまう…
（描画が後勝ちだとすると）手前にくる点を後から描画するようにできるといいんだが…
色の濃淡で表現しようとしたけど、色は高さで使ってしまっていて2軸で色を反映する機能はない…（高さの色分けを諦める手もあるけど、そうしても濃淡だけではあまり根本解決にはならなかった）
等高線
描画順のところと関連するけど、Excelの等高線のようにしっかり線を引いて色分けしたい。そのために、高さでグルーピングして何らか順番をつけて「多角形」または「パス」で描画したい。元データをそのように作ってしまえばできそうだけど汎用性がなくなってしまうので Tableau の機能で閉じて実現したい…
軸、目盛り
Excel の図のように x,y,z 軸と目盛りを表示したい。図の上下左右の回転に伴って一緒に回転するように…

さいごに

まだまだとりあえず平面に落とし込んだだけですが、基礎部分はできたので上記のやりたいことを今後拡張していきたい。
3Dプロットを業務上使いたい場面が出てくるかは分かりませんが…

以上、何かの参考になれば幸いです。

続編はこちら（上記の「やりたいけどやれてないこと」を実現しています）

Tableau で3Dプロットをしてみた