動機
筆者は複数のメーカ、大学で機械学習を応用した研究開発、製品開発を経験した後、現在はIT会社で人工知能部門でのマネージメント業務に従事しています。機械学習システムの検証技術の動向について、非専門家である自分が一定レベルで概要を理解すること、また、勉強した結果をシェアすることで同様のニーズを持つ方が短時間で知識を得るために役に立てて頂くことがこの記事を書く動機です。
想定する読者
企業内で機械学習システムの検証試験の内容に関与される方、例えば以下のような方を対象としています。
- 機械学習システムの検収条件を顧客と擦り合わせることができずにいるプロダクトオーナ
- 開発チームが提案する機械学習システムのテストプランが十分か判断できないマネージャ
- 開発部門が提案する検証試験の内容が十分ではないと考えているQAエンジニア
- 品質担当部門と検証試験の内容について合意できずにいる開発担当エンジニア
前置き
伝統的なソフトウエア開発では、要求仕様(requirements specification)を満足することが、ソフトウエアの出荷または検収のための必要条件とみなされます。要求仕様の一つ一つは、検証試験(verification procedure)として具体的な手順に落とし込まれます。品質保証部門のテスト担当者は検証試験を実施し、システムの挙動及び出力が事前に定義された期待と整合するか否かを確認します。全ての検証試験がパスすれば、品質保証部門と開発部門は出荷可の必要条件を満たしたと判断することができます。また、発注元は検収の必要条件が満たしたとみなすことができます。出荷、検収という観点から、ソフトウエアの品質をどのように保証するべきか、という観点についてステークホルダー間で合意がある状態と言えます。
一方、機械学習システムの場合、要求仕様そのものを客観的に記述できない、あるいは現実的なテスト手順に落とし込むことが困難な場合があります。画像分類システムを例にすると、システムに人間と同程度の識別能力を求める場合、そもそも人間と同程度とは何か、厳密かつ客観的に表現することはで困難です。また、考えられうる全ての画像に対して正解を人間が人手で与えることは事実上不可能です。実際、例えば512x512x8 bitのグレースケール画像であれば$256^{262144}$乗通りの画像に正解を与える必要があります。
このような場合、要求仕様に基づく検証試験を定義ないし、実施することが困難であるため、伝統的なソフトウエア開発に慣れ親しんできたステークホルダー間でソフトウエア品質の保証に関する考え方の食い違いが発生することになります。検収を行う顧客や品質保証の責任担当部門は極力仕様を明確にして仕様を満足するように要求する一方で、開発担当部門は仕様を明確化することは技術的に困難であるとして、考え方の食い違いが顕在化するかもしれません。
このようなギャップを解消するためには、機械学習システムの品質をどのように保証するべきか、ステークホルダーが共通の認識をもつ状態を実現していることが前提になります。将来的には学会のガイドラインのようなものが現れ、社会に普及することで徐々に共通の認識が普及することが期待されますが、一方の現実では、明日の契約、明後日のリリースに向けて、実務担当者である我々は現実的な解を見つけていく必要があります。そのためにはソフトウエア検証試験(Verification)に関連した研究動向の実情をある程度のレベルで理解しておき、現状何ができるのか、あるいはできないのか、共通の認識をステークホルダーで共有することが重要と思います。
論文は多量にあって何から読むものか迷いますし、専門的過ぎてわからなかったり、本業の間で勉強する時間がもてなかったりします。以下では、機械学習システムの検証技術の動向について短時間で概要を理解するために代表的な論文をピックアップして簡単な解説を試みてゆきたいと思います。簡単とはいっても、1回の記事で1論文とし、何回かに分けて執筆したいと考えています。
論文の選択方法
GitHub上に集積されているVerificationとTestingに関する文献集([1])を参照しました。この中から2017,2018年中に発表があった文献のabstractに目を通し、被引用数が多く重要と思われた、Xiaowei Huang, Marta Kwiatkowska, Sen Wang, Min Wu ,”Safety Verification of Deep Neural Networks”,を紹介しようと思います([2]。2018/12/1時点でGoogle検索にて136件引用)。これはOxford大学のMarta Kwiatkowska教授の研究グループによるもので、2017年CAV(Computer Aided Verification)にも発表されています。内容はArxivのみでなく動画でも確認することができます([3])。
Safety Verification of Deep Neural Networks
議論の対象
はじめ論文のタイトルをSafe Verificationと読み違えてしまったのですが、このタイトルでいうところの”Safety”とは、一般用語としての”安全な”という意味ではありません。”Safety”いう概念を、ある特定の入力データに対して、十分「近い」範囲では出力が同じになること、として定義しています。そしてSafety Verificationとはその検証、つまり、ある特定の入力データに対して、あらかじめ定義した十分「近い」範囲では出力が漏れなく同じになることを確実に判定することを指しています。言い方を変えると、入力画像に対して十分「近い」範囲における敵対的サンプル(adversarial example)を網羅的に探索する手法の提案になっています。なお、以下の記述では本論文に沿って、画像分類のネットワークを想定して説明します。
注意する必要があるのは、この論文で紹介されているのは、あくまで与えられた「特定の入力データに近い」領域を網羅的に探索して敵対的サンプルを発見する手法であり、入力データの空間に属する任意の敵対的サンプルを網羅的に見つけ出す方法ではないことです。また、「特定の入力データに近い」という点にも難しい問題が含まれていて、入力データの空間の中で定義される距離(ex. $L_2$ノルムなど)に基づく「近さ」は、人間が認知する心理的な「近さ」を必ずしも反映していません。従って、与えられた入力データの「近く」で$L_2$ノルムなどを使って定義した領域の中に含まれない敵対的サンプルが存在しうることになります。また、画像自動分類の性能を評価する場合、データを誤分類する確率としてのリスクなど何らか統計的な尺度で評価することも多いと思いますが、本論文ではモデルの統計的な性質については議論の対象外としています。
問題を解く枠組み
画像分類のニューラルネットは$n$次元実ベクトル空間$R^{n}$から$m$次元実ベクトル空間$R^{m}$への写像とみなすことができます。例えば512x512x8 bitのグレースケール画像を10クラスに分類するネットワークであれば、$n=256^{512x512}$, $m=10$となります。ニューラルネットワークを表す写像を$f$とすると、敵対的サンプルの探索問題は、
*$R^{n}$上の与えられた入力データ$x$の近傍$η$に$f(x)$と$f(y)$が異なるような$y$が存在するか判定し、存在するならばその値を求める *
問題と言えます。ここで、$f$はニューラルネット全体を表現する関数であり、非常に多数のフィルタ演算、活性化関数、max pooling等々によって記述されます。近傍$η$を入力データの周辺に定義した列挙可能な有限個の点の集合とすれば、非常に多数の実数変数の等式、不等式とそれを満足する解を探索する問題として扱うことができます。ここでは大規模な変数をもつ問題に対して効率的に解を探索する手法が必要になります。
SAT/SMT
この問題はSAT(satisfiability problem:充足可能性問題)、SMT(Satisfiability Modulo Theory) の枠組みで扱うことができます。筆者はSAT、SMTについて専門家ではないので、この記事の中できちんと解説することはできないのですが、参考文献([5][6][7][8][9][10])を読んで得た知識を元に最低限の説明を試みたいと思います。間違っているところがあればご指摘頂ければ幸いです。
SATは一つの命題論理式が与えられたとき、その論理式を真にするような変数の値の組み合わせは存在するか、という問題です。SATは計算機科学における最も基本的で本質的な組合せ問題で、システム検証、プランニング、スケジューリング,定理証明,制約充足問題など様々な分野で活用されており、近年では$10^{6}$~$10^{7}$の大規模な数の変数をもつSATを高速に解くアルゴリズムが開発されているようです(参考文献による)。
SATを解くアルゴリズムを実装したソフトウエアはSATソルバと呼ばれます。SATソルバは入力として命題論理式を受け取り、その式全体の値が真になるような変数の値を探索し、存在する場合はその値を出力します。[5]には数独を命題論理式に落とし、SATソルバによって解く例がわかりやすく説明されています。
SATで扱う対象は命題論理で、直接、述語論理を扱うことができません。これに対して、述語論理を扱えるようにしたものが背景理論付きSATとも呼ばれるSMTです。SMTはSATを理論ソルバ(例えばLinear Programmingなどのソルバ)と組み合わせます。[5]に挙げられている例では、等式、不等式からなる述語論理を命題論理式に落とした上でSATソルバを適用し、適当な真偽の割り当てによって充足可能であることがわかったら、今度はLinear Programmingなどの理論ソルバを適用して解の存在を検証する。解が存在しなければ、さらに制約として命題論理式に追加する例が記載されています。
SATを敵対的サンプルの探索に活用する考え方そのものは本論文が初めてではなく、大規模問題を扱えるように急速に発展したSAT/SMTソルバを活用して敵対的サンプルの有無を判定する、というアプローチは本論文も含め機械学習のVerificationの分野における研究の一つの方向性になっているようです。
本論文の特徴
本論文に固有の特徴として以下が挙げられます。
-
与えられたデータを中間層で操作(manipulation。分類結果が変化しないような操作の意味)して敵対的サンプルを探索します。着目する層の直前の層における特徴量の変化に対して敏感に変化する特徴量を選択的に操作することで、敵対的サンプルの検出に有利としています。実験では選択した特徴量の値を事前に決めた一定量、増減させています。
-
探索領域を層から層へ伝播させながら、より精細に探索を行なってゆきます。探索領域を限定することで、多層のニューラルネットにおける敵対的サンプルの探索を効率的に行うことが可能なフレームワークとなっています。これは次の手順で進みます。
- まず、第$k$層において選択された特徴量群を操作して敵対的サンプルを探索します。この時、探索した領域をηkとおきます。
- 敵対的サンプルがηkに存在しなければ、次の第$k+1$層の探索に入ります。まず探索すべき領域ηk+1を、領域ηk+1の逆像が第$k$層において領域ηkを内部に含むように設定します。具体的には第$k$層における探索領域ηkの外接矩形の第$k+1$層における像を領域ηk+1とすることができます。この条件を課することで第$k+1$層では常に第$k$層で探索した領域をより詳細に探索し直すことができます。
- 次いで領域ηk+1の内部で行う操作(manipulation)を求めます。第$k+1$層では第$k$層における操作を精細化(refine)します。第$k$層で0から1に特徴量を変化させた時に(この場合、第$k$層での操作は「1増やす」ことに相当。)、第$k+1$層で特徴量が0から10に変化したとすると、第$k+1$層での操作を同じく「1増やす」ことと定義すれば、第$k+1$層での操作は第$k$層での操作を精細化(refine)したものとなります。実験では高速化のため、第$k+1$層では操作の対象とする特徴量の数は事前に決めておきます。第$k$層でのmanipulationに対して「最も変化した」上位数個の第$k+1$層の特徴量を操作対象とします。
- これで第$k+1$層において探索すべき領域と操作が求まったので、第$k+1$層における敵対的サンプルを探索します。
- 以後このステップを一層一層繰り返します。
一方で、実験では色々な仮定を導入しており、必ずしも厳密ではない探索方法となっています。例えば、
-
与えられたデータ(中間層も含む)に対して、それより「小さい」操作を加えても出力結果は変わらない、という最小の操作(minimal manipulation)という概念を定義しています。実験的には天下り的にある特徴量を単位量変化させることをminimal manipulationとしています。単位量の変化が本当にminimal manipulationになっていない可能性があります。
-
前述のように、実験では、特定の特徴量を増減させて敵対的サンプルを探索しています。従って、他の特徴量を増減させて得られる敵対的サンプルが存在する可能性があります。
これが良くないというよりは、このような仮定をいれることで、多層のニューラルネットにおける敵対的サンプルを検出するフレームワークが提供されています。
実験結果
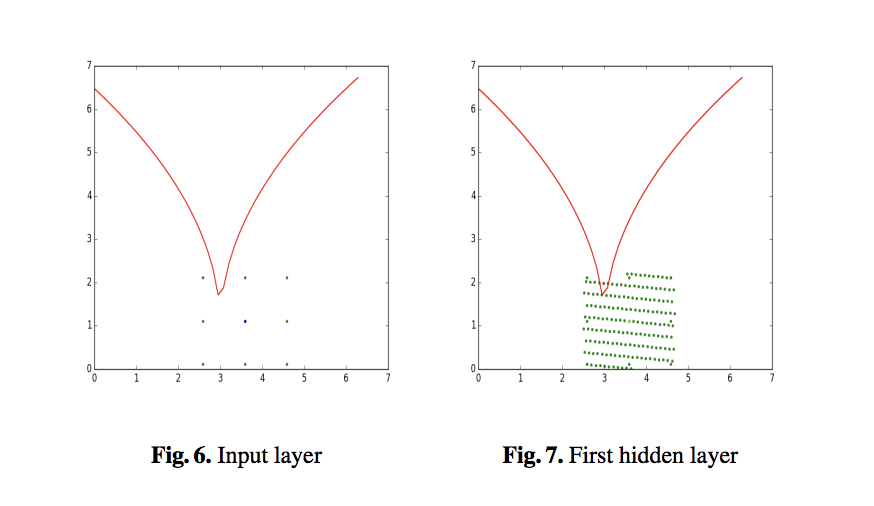
こちらは2層の隠れ層を持つtoy networkでの実験結果です。赤い曲線を境界として2次元の入力データ空間が二つのクラスに分割されています。赤い曲線の境界に近い(3.59,1.11)がデータとして与えられ、敵対的サンプルを見つけることが課題です。Fig. 6はこの点を中心とする間隔1.0、縦横3X3の格子点(緑の点)を探索したものの、格子点は全て赤い曲線の下に位置していて敵対的サンプルが見つからなかった様子を示しています。一方で、Fig. 7は隠れ層の一層目で最も変化の大きい2個の特徴を選択し、入力層で与えられたサンプル(3.59,1.11)の隠れ層の一層目における像を中心とする間隔1.0の格子上で探索した結果を入力層に逆写像した結果をプロットしてあります。ここではadversarial exampleが見つかっています(一部の点が赤い曲線の上に位置している)
こちらはGTSRB(ドイツの道路標識データセット)での結果です。隠れ層の一層目で1000個の特徴を選択し、間隔1.0の格子上で探索し発見した敵対的サンプルを入力層に逆写像した画像を示しています。

終わりに
特定の入力データの周辺に定義した狭い領域の中において敵対的サンプルの有無を検証する手法が今回紹介した論文の扱う問題です。論文では中間層で特徴量を操作し、一層一層探索を精細化してゆく点が新しいとされています。
検証試験に関わる企業の担当者の立場としては、任意の敵対的サンプルの有無を確実にリストアップできる技術が欲しい、あるいは敵対的サンプルが生じないネットワークが欲しいと言いたいところです。しかし、特定データという限られた問題設定に対してでも敵対的サンプルを完全にリストアップすることはまだ研究レベルという前提にたって実際の検証試験は検討する必要があります。
なお、機械学習システムの検証・テスティング研究動向については、国立情報学研究所石川先生の講演スライド([4])のまとめがあり、参考にさせて頂きました。形式的検証技術(SMTソルバー)の応用例として本文献も参照されています。研究動向としては他の重要な方向性もあると思いますが、別稿にて論文紹介の追加を計画したいと思います。
参考資料
[1] https://github.com/TrustAI/Literature-on-DNN-Verification-and-Testing/blob/master/verification.md.
[2] Xiaowei Huang, Marta Kwiatkowska, Sen Wang, Min Wu ,”Safety Verification of Deep Neural Networks”, https://arxiv.org/abs/1610.06940.
[3] https://www.youtube.com/watch?v=XHdVnGxQBfQ.
[4] 石川, ”機械学習における品質保証のチャレンジ”, トップエスイーシンポジウム.http://research.nii.ac.jp/~f-ishikawa/work/1712-JEITA_QA4ML.pdf.
[5] http://d.hatena.ne.jp/ku-ma-me/20080108/p1.
[6] https://ja.wikipedia.org/wiki/%E5%85%85%E8%B6%B3%E5%8F%AF%E8%83%BD%E6%80%A7%E5%95%8F%E9%A1%8C.
[7] 鍋島, 高速SATソルバーの原理, http://www-erato.ist.hokudai.ac.jp/docs/seminar/nabeshima.pdf.
[8] 酒井, Proof Summit 2015, https://www.slideshare.net/sakai/satsmt
[9] https://en.wikipedia.org/wiki/Boolean_satisfiability_problem
[10] https://en.wikipedia.org/wiki/Satisfiability_modulo_theories