Pythonで円運動を追従するPID制御のアニメーションを描画

#はじめに
最近、pythonでアニメーションを簡単に描けることを知り、何か題材はないかと探していたのですが、学部時代に制御工学で習ったPID制御に思い当たりました。
そこで、本記事ではPID制御をpythonで実装し、その様子をアニメーションで可視化します。
ただ、どうせなら少しひねったものをしてみたかったので、今回は円運動する質点を追従する制御を実装してみます。（これはこれで使い古されたネタかも）

#サンプリング方式に基づいた操作量の求め方
操作量はこちらの記事を参考に以下の式で求めます。

MV_n = MV_{n-1} + K_p(e_n-e_{n-1}) + K_i e_n + K_d[(e_n-e_{n-1}) - (e_{n-1}-e_{n-2})]

ここで、Kp,Ki,Kdは比例制御、積分制御、微分制御の係数です。
en,en-1,en-2は現在、前回、前々回の偏差です。MVn,MVn-1は現在、前回の操作量です。
今回は、操作量を「制御する質点のx,y方向の速度」とし、偏差は「x,y方向の目標との距離」とします。

#プログラム
プログラムを順に追っていきます。
なお、円運動する質点を質点A、制御する質点を質点Bとします。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

fig = plt.figure()

kp = 1 # P制御
ki = 1 # I制御
kd = 0 # D制御

bx = 0; by = 0 # 初期位置
bvx = 0; bvy = 0 # 初期速度
errorx = [0]*3 # [0]は現在の偏差 [1]はひとつ前 [2]はふたつ前
errory = [0]*3

matplotlibの機能でアニメーションを描くため、importしておきます。
各制御の係数や質点Bの初期位置、初期速度を設定します。
偏差は前々回の分まで保持する必要があるのでリストにしておきます。

次に、本プログラムの骨子であるPID制御の部分です。

def update(frame):
    global bx,by,bvx,bvy,errorx,errory
    plt.cla() # 現在描写されているグラフを消去
    plt.xlim(-2, 2)
    plt.ylim(-2, 2)
    dt = 0.05
    t = frame * dt
    ax,ay = np.cos(t),np.sin(t)
    # 偏差
    errorx[0] = (ax - bx) 
    errory[0] = (ay - by) 
    # PID制御
    bvx += kp * (errorx[0]-errorx[1]) + ki * errorx[0] + kd * (errorx[0] - 2*errorx[1] + errorx[2])
    bvy += kp * (errory[0]-errory[1]) + ki * errory[0] + kd * (errory[0] - 2*errory[1] + errory[2])
    bx += bvx * dt 
    by += bvy * dt 
    plt.plot(ax,ay,'o')
    plt.plot(bx,by,'o')
    for i in (1,0):
        errorx[i+1] = errorx[i]
        errory[i+1] = errory[i]

最初の一行は、bx,by...がグローバル変数であることを宣言してます。これがないと変数を認識してくれませんでした。元からグローバル変数な気もするのですが、詳細不明。
plt.xlimでグラフの領域を制限します。今回は、質点Aが半径1の円運動を行うので-2~2を描画範囲としました。
dtは時間ステップです。1フレーム（更新）あたりdt秒経過したとして計算を行います。（正直物理的な意味は薄いと思います）
ax,ayは質点Aの座標です。前述の通り円運動を行います。
偏差、PID制御については定義の通り実装します。
末尾部分では偏差の更新を行い、前回の偏差を前々回に、現在の偏差を前回に移しています。

最後に、アニメーションを描画する部分です。

ani = animation.FuncAnimation(fig, update, interval=30, frames=251)
# ani.save("P.gif", writer="imagemagick")
# plt.close()
plt.show()

intervalはフレームが表示される間隔（ミリ秒）です。小さいほど滑らかに動きます。30だとフレームレートでいうと30fps程度です。
framesは総フレーム数です。丁度質点Aが二周するように調整しました。
gifを保存する場合は、コメントアウトを外します。

各制御の比較

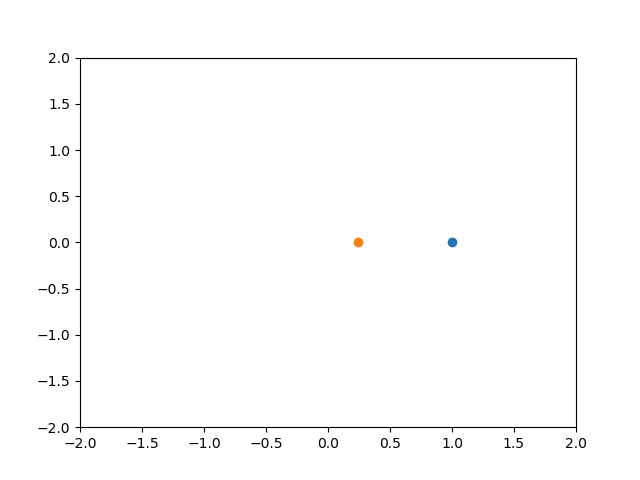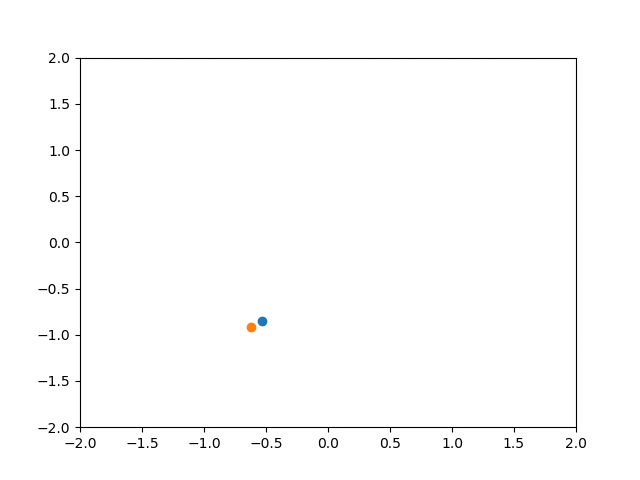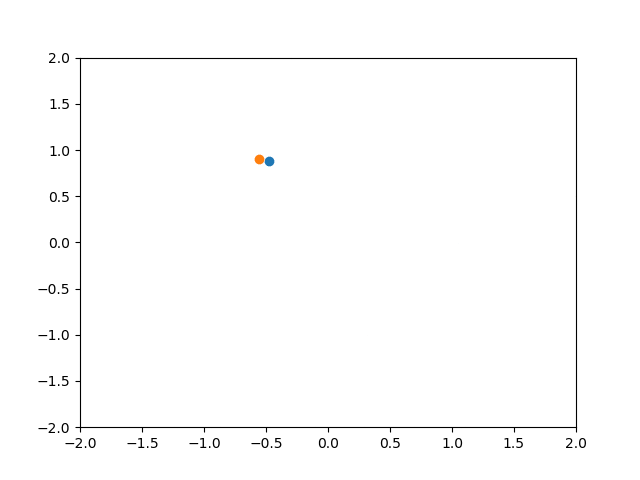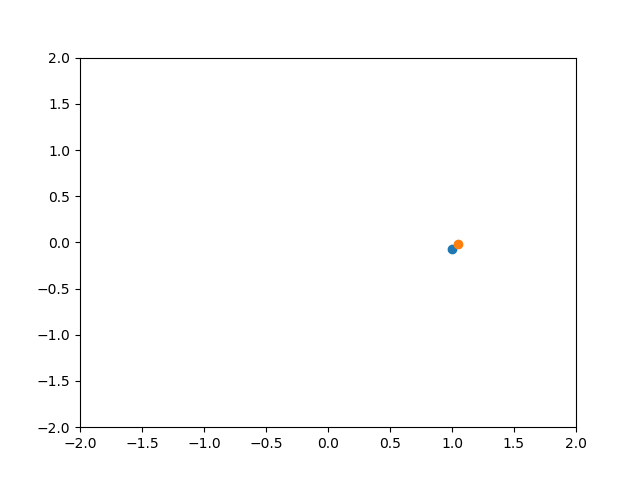
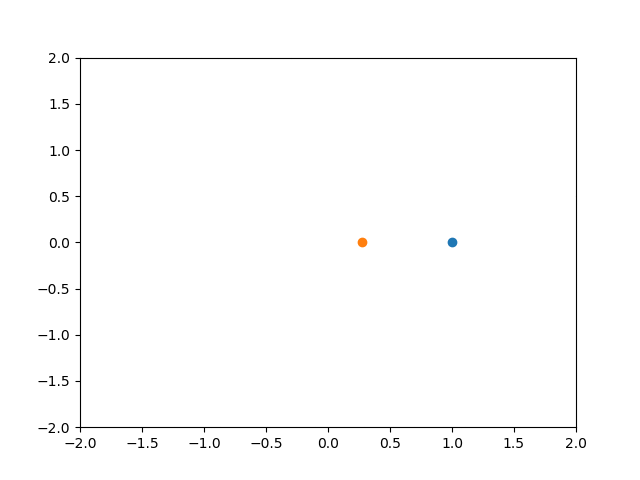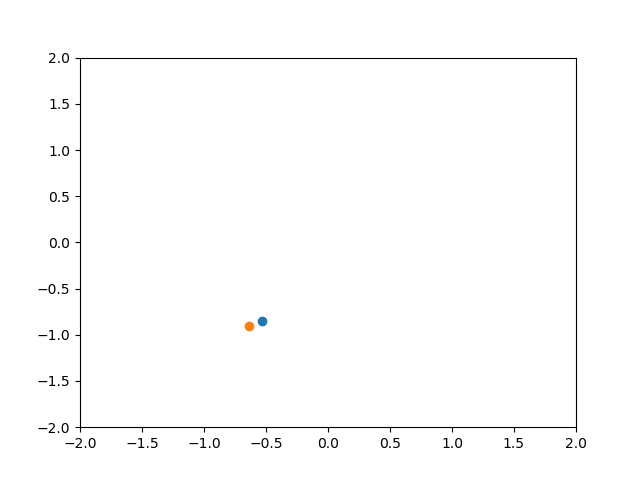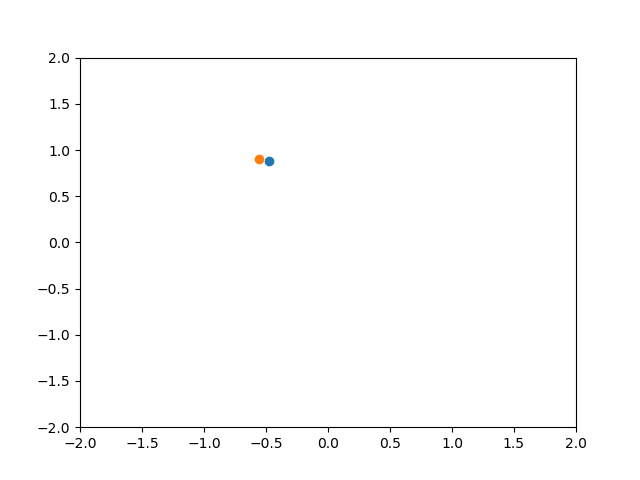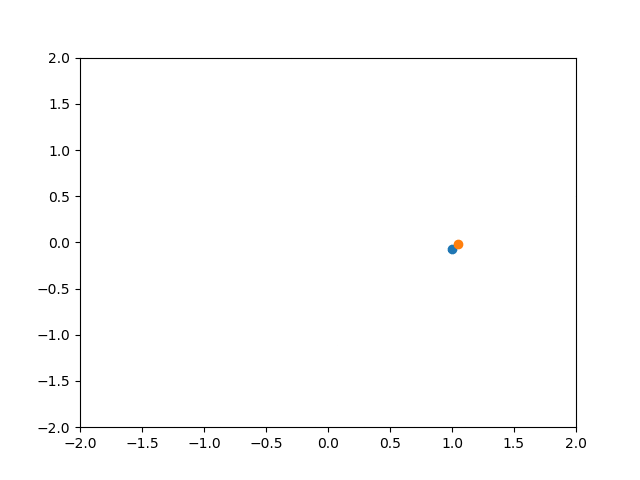
P制御 Kp = 1 Ki = 0 Kd = 0

質点Aが青色の点、質点Bが橙色の点です。
早い段階で安定（質点間の距離がほぼ一定）しますが、質点AとBの間にはかなりの偏差が残ってしまっています。
P制御（比例制御）は定常偏差が残ってしまうことが特徴の一つで、今回の結果はその傾向をよく示しています。
また、x,y方向にのみ着目すると目標に対して振動しているのに対し、質点間の距離に着目すると安定しているのは面白いです。円運動はx,y方向に着目すると振動運動だからでしょうか。

PI制御 Kp = 1 Ki = 1 Kd = 0

P制御の時と比べてしばらく振動していますが、最終的な定常偏差はかなり抑えられています。
I制御（積分制御）は主に定常偏差を解消するために用いられ、今回の結果はその様子がよく分かります。

PID制御 Kp = 1 Ki = 1 Kd = 1

PI制御と比べてもあまり違いは分かりませんでした。
一般に、D制御はP制御やI制御によって生じる急激な変化を抑えることで、振動を防ぎ応答を早くする働きを持ちます。
今回は、目標が動いているためD制御が有効に働かなかった可能性があります。

#まとめ
PID制御をpythonを用いてアニメーションで可視化することが出来ました。
このような単純な式で表される制御でも、入力が対象の座標しかない（速度や加速度は不明）にも関わらず、十分追従できていたのは驚きでした。
また、プログラミングし可視化することで、教科書を眺めていたころに比べてより実感を持って理解できたように思います。
最後に、参考にしたサイトを列挙します。

#参考

PID制御

pythonでアニメーション