湧き出しと吸い込み(ソースとドレイン)をもつ有向ネットワークに対して、そこを流れる水量の最大値を求める方法がFord-Fullkersonアルゴリズムです。
解説記事は色々あるのですが、qiita上でc++のコードが見当たらなかったので載せてみました。
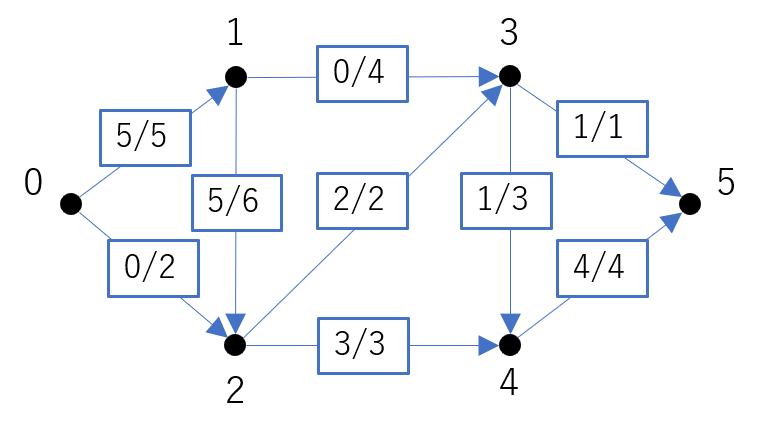
例えば次のネットワークを入力とします。
最初の行はノード数とエッジ数、2行目はソースとドレインのノード番号です。
3行目からは各エッジの始点、終点、エッジのコスト(容量)です。
6 9
0 5
0 1 5
0 2 2
1 2 6
1 3 4
2 3 2
2 4 3
3 4 3
3 5 1
4 5 4
図で表すと次のようになります。
アルゴリズム
ネットワークのソースを$s$、ドレインを$d$、各頂点を$v_i \in V$、$v_i$から$v_j$への有効エッジを$e=(v_i,v_j) \in E$、その容量を$C[e]$とします。
ソースからドレインに水を流したとき、パスを1つ選んでその各エッジで流せる流量の最小値$\delta$を求めます。するとすべてのエッジで$\delta$だけ流すことが可能なので、$\delta$だけ流すとすると各エッジの残りの容量は$C[e] \rightarrow C'[e] = C[e]-\delta$となります。この更新後のグラフで再び流量の最小値を求めてそれを流すということを繰り返して流量を増やしていく方法がFord-Fullkersonアルゴリズムの基本方針です。ここで、この最小値$\delta$はDFSやBFSによるパスについての全探索を用いて求めることができます。
しかし、一般にこの今のやり方ではネットワークの最大流量に到達するとは限りません。なぜなら、それまでに流した流量を一部のエッジで減らして各点で入出量が釣り合うようにしなければならないからです。そこでそれまでにエッジ$e$へ流した流量$f(e)$を減らすという操作の代わりに容量$f(e)$で逆向きのエッジ$-e=(v_j,v_i)$に水を流すというように取り扱います。この逆向きのエッジ(残留エッジ)を付け足したネットワークで最小の流量だけ水を流すというのが、Ford-Fullkersonアルゴリズムの肝になります。
例えば、容量3のエッジ$(A,B)$に水を1だけ流した時、流す前は
C[(A,B)]=3 \\
C[(B,A)]=0
だったのが、水を1だけ流して
C[(A,B)]=2 \\
C[(B,A)]=1
と更新されます。
ちなみに各エッジの容量については
C[e] \geq 0 \\
C[-e] \geq 0 \\
C[e] + C[-e] = const.
という制約があります。
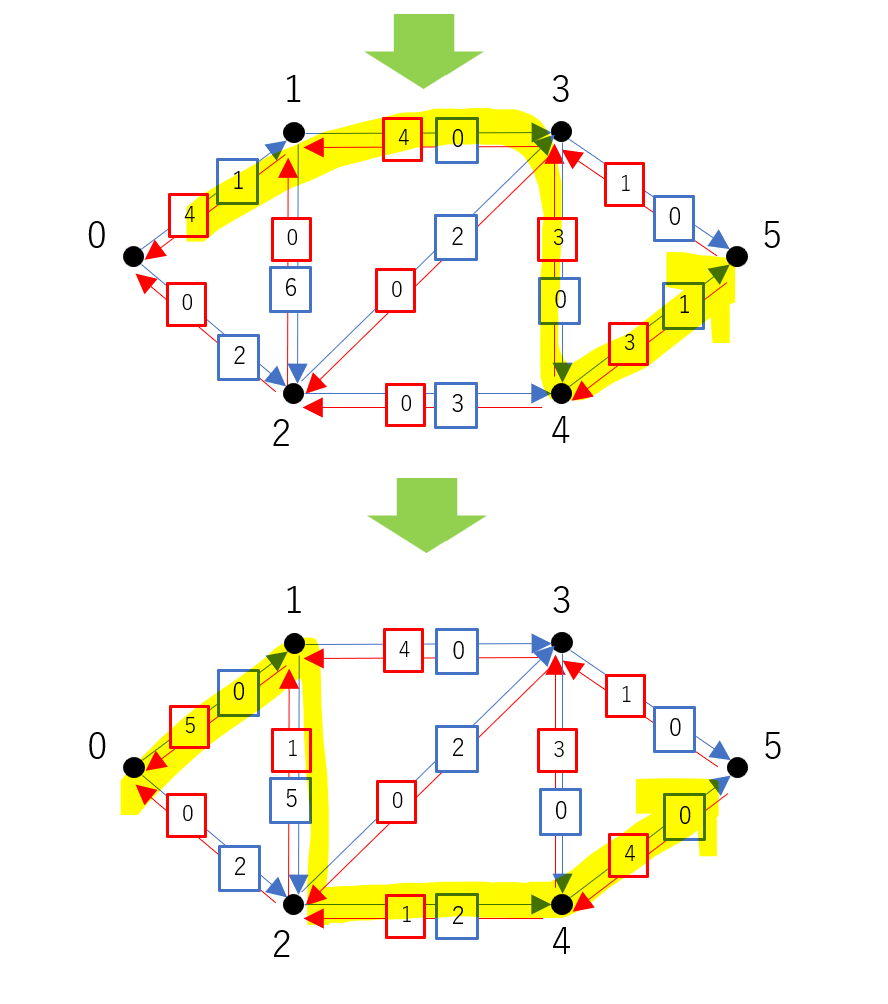
今の例で試してみると、以下のようになります。青色が元のネットワーク、赤色が残留ネットワークです。
これ以上操作を続けることはできますが、ソース・ドレイン間の流量に変化はありません。
(3回目の操作で既に最大値に達していますが、以下のコードと合うようにさらに2回操作を繰り返しています。)
また残留ネットワークの各エッジの容量は実際に流した流量になっています。
実装
Ford-Fullkersonアルゴリズムに従ってネットワークフローを計算する構造体を以下のようにしました。
#include<bits/stdc++.h>
using namespace std;
//Ford-Fulkerson algorithm
//construct residual network => find augumented path
//~O(V^2*E)
struct network{
struct edge{
//rev: id of array G[to] from the front for the starting point; not id of node
int to, cap, rev;
//judge original or residual
bool forward;
};
int n;//# of node
int source, drain;
vector<vector<edge>> G; //residual graph (same as given network at first)
vector<vector<pair<int,int>>> flow;
vector<bool> used; //flag of dfs
network(int n_, int s_, int d_): n(n_),source(s_),drain(d_),G(n_,vector<edge>()),used(n_,false),flow(n_,vector<pair<int,int>>()){}
//add edge to the graph
void add( int from, int to, int cap ){
G[from].push_back((edge){ to, cap, (int)G[to].size(),true});
//reverse path ( cap is 0 <=> not exist at first)
G[to].push_back((edge){ from, 0, (int)G[from].size()-1,false});
return;
}
//u->v
//f: flow of augumented path (= bottleneck capacity) between u->v
//search bottleneck with dfs
int dfs( int u, int v, int f ){
if(u==v) return f;
used[u] = true;
for( int t=0; t<G[u].size(); ++t ){
edge &e = G[u][t]; //pointer ref to overwrite G[u][t]
if(!used[e.to] and e.cap>0){
int d = dfs(e.to, v, min(f,e.cap));
if(d>0){
e.cap -= d; //decrease cap. of forward edge
G[e.to][e.rev].cap +=d; //increase cap. of reverse edge
return d;
}
}
}
return 0;
}
void __init__optimul_graph(){
for( int v=0; v<n; ++v )for( edge e : G[v] )if(!e.forward){
flow[e.to].emplace_back(v,e.cap);
}
return;
}
int maxflow(){
int inf = numeric_limits<int>::max();
int f=1;
int ans=0;
while(f>0){
used = vector<bool>(n,false);
f = dfs(source,drain,inf);
ans += f;
}
__init__optimul_graph();
return ans;
}
};
構造体networkはノード数とソース、ドレインのノード番号を与えて宣言します。
メンバ関数は
- add
- maxflow
の2つで、関数addはグラフにエッジを追加する操作になっていて、maxflowはグラフの最大流計算を実行し、その最大流量を返す関数です。
また、flowはエッジの始点についての配列となっていて、最大流を流すときの各エッジの終点と流量のペアを格納しています。
int main(){
//# of node & edge
int n,m;
cin >> n >> m;
//source &drain in the network
int s,d;
cin >> s >> d;
//declear network struct
network net(n,s,d);
//add edge
int from,to,cap;
for( int i=0; i<m; ++i ){
cin >> from >> to >> cap;
net.add(from,to,cap);
}
cout << net.maxflow() << endl;
for( int v=0; v<n; ++v )for( auto p : net.flow[v] ){
cout << v << " " << p.first << " " << p.second << endl;
}
return 0;
}
すると最大流量は
5
で、それを実現する各エッジの流量の一例を
始点、終点、流量の順に列挙すると、
0 1 5
0 2 0
1 2 5
1 3 0
2 3 2
2 4 3
3 4 1
3 5 1
4 5 4
です。図にすると以下の通りです。
参考文献
- Jon Kleinberg, Eva Tardos, 「Algorithm Design」
- 秋葉拓哉, 岩田陽一, 北川宜稔, 「プログラミングコンテストチャレンジブック」 第2版