はじめに
以前、「機械学習の分類」で取り上げたアルゴリズムについて、その理論とpythonでの実装、scikit-learnを使った分析についてステップバイステップで学習していく。個人の学習用として書いてるので間違いなんかは大目に見て欲しいと思います。
今回は基本の「単回帰分析」。参考にしたのは次のページです。
基本
$ x $軸、$ y $軸からなる平面上の直線は$$ y=Ax+B $$として表される。$ A $は傾きで$ B $は切片とも言いますね。
多数の$ x $、$ y $の組み合わせに、いい感じの直線を引くための$ A $と$ B $を求めるのが単回帰です。人間ならなんとなく「こんな感じかな?」という直線を引くことができるが、これをコンピュータに引かせようというアプローチですね。
お題
pythonのscikit-learnにはいくつかのテスト用のデータセットがある。今回はその中からdiabetes(糖尿病データ)を使う。コードはGoogle Colaboratoryなんかで試すことができます。
前準備
まずはテストデータを眺める。
詳しい説明はAPIドキュメントに記載があるが、10個のデータに対してターゲット(1年後の進行状況)が用意されている。
10個の要素のうち、BMIのデータがどう影響するかを散布図で見て見たい。なぜBMIかはいずれ触れる。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
diabetes = datasets.load_diabetes()
df = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
x = df['bmi']
y = diabetes.target
plt.scatter(x, y)
横軸がBMI、縦軸が進行状況です。図で見るとなんとなく右肩上がりの直線を引けそうですね。

単回帰の解き方
与えられた$ N $個の$ (x, y) $列に対し、いい感じの直線を引くためのパラメータ$ A $と$ B $は、直線$ y = Ax + B $と$ i $番目の $(x_i, y_i) $との差の二乗の和を最小にする$ A $と$ B $を探せばいいことになる。つまり、$$ \sum_{i=1}^{N} (y_i-(Ax+B))^2 $$が最小となるような$ A $と$ B $を求めていく。
具体的には、上式を$ A $と$ B $で偏微分し、連立方程式を解くことになるのだが、割愛する。是非紙と鉛筆で書いてみるといいと思います。$ \sum_{i=1}^{N}x_i $が$ n\bar{x} $、$ \sum_{i=1}^{N}y_i $が$ n\bar{y} $で表すと$ A $と$ B $はそれぞれ$$ A = \frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^{n}(x_i-\bar{x})^2} $$ $$ B= \bar{y}-A\bar{x}$$となる。ここまでくれば与えられた$ (x_i, y_i) $を上式にぶち込めば$ A $、$ B $は簡単に求まる。
pythonで愚直に実装してみる。
$ A $、$ B $を素直にコーディングしてもいいのだが、numpyに便利な関数がすでにあるのでそれを使う。$A$の分母は$x$列の分散(の$1/n$)、分子は$x$列と$y$列の共分散(の$1/n$)である。
S_xx = np.var(x, ddof=1)
S_xy = np.cov(np.array([x, y]))[0][1]
A = S_xy / S_xx
B = np.mean(y) - A * np.mean(x)
print("S_xx: ", S_xx)
print("S_xy: ", S_xy)
print("A: ", A)
print("B: ", B)
結果は以下である。なお、分散(var)は、標本分散と不偏分散というのがあり、あとで説明するscikit-learnは不偏分散であるため、不偏分散で計算する。標本分散と不偏分散については別で説明する。
<追記>ありました
S_xx: 0.0022675736961455507
S_xy: 2.1529144226397467
A: 949.43526038395
B: 152.1334841628967
実はnp.cov[0][0]はxの分散なので計算する必要は無いのだが理解のために上記のようにしている。ここで求めた直線をさきほどの散布図にプロットしてみる。
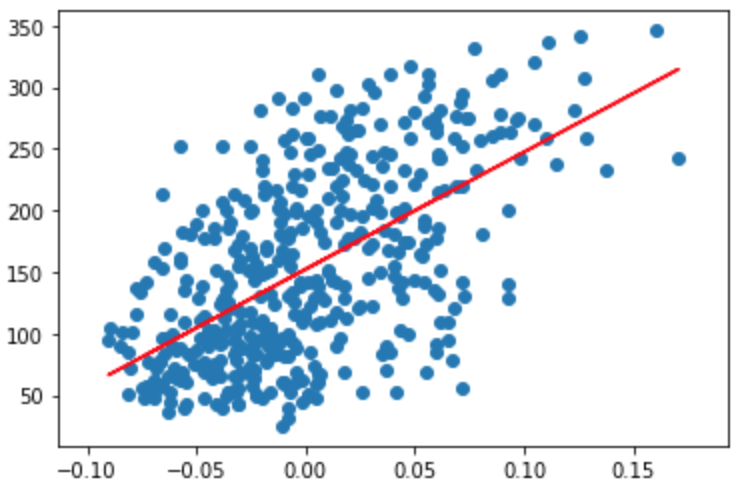
plt.scatter(df['bmi'], diabetes.target)
plt.plot(df['bmi'], A*df['bmi']+B, color='red')
結果のグラフを見るとなんとなくいい感じの直線が引けていることがわかる。
同じことをscikit-learnでやってみる
同じことをscikit-learnでやるともっと簡単になる。なんとなく使えてしまうのがわかると思うが理論的なところをわかった上で使うと全然腹落ちがちがうというのも理解いただけるだろうか。
from sklearn.linear_model import LinearRegression
model_lr = LinearRegression()
model_lr.fit(x.to_frame(), y)
これだけです。fitメソッドの第一引数はpandas.DataFrameしか受け付けないらしいのでto_frameで強制的にDataFrameにする必要がある(参考)。
傾きと切片はそれぞれ、coef_とintercept_なので(API参照)、先ほどの結果と比較してみる。
print("coef_: ", model_lr.coef_[0])
print("intercept: ", model_lr.intercept_)
coef_: 949.4352603839491
intercept: 152.1334841628967
同じ結果になりましたね。
さらなる理解(相関係数Rと決定係数R2)
相関係数
相関係数(correlation coefficient)Rは、2つの変数間にどれくらいの関連性があるか(どれくらい影響を及ぼしあっているか)を表す係数で、-1〜1の数字をとる。
相関係数$r$は$x$と$y$の共分散をそれぞれの標準偏差で割った値で、numpyではcorrcoefメソッドで求められる。
r = S_xy/(x.std(ddof=1)*y.std(ddof=1))
rr = np.corrcoef(x, y)[0][1]
0.5864501344746891
0.5864501344746891
こちらも同じ値ですね。値が大きいほど、それぞれの関連性が強いということになります。
決定係数
決定係数は、求めた直線と実際のデータがどれくらい合致しているかの指標で、1に近いほどもとのデータに近いということになる。
決定係数は、全変動と残差変動という値をもとに求めることができ、相関係数の二乗と等しくなる。くわしくはこちらを参照。
決定係数はLinearRegressionクラスのscoreメソッドで求められる。
R = model_lr.score(x.to_frame(), y)
print("R: ", R)
print("r^2: ", r**2)
R: 0.3439237602253803
r^2: 0.3439237602253809
等しくなりますね。
まとめ
単回帰分析について、理論を確認しながらpythonの実装を試してみた。回帰直線を引く方法と、求めた直線がどれくらいもとのデータを表現しているかがわかることを理解できたと思う。
ちなみにターゲットに対してBMIを選んだのは、相関係数がもっとも高かったからである。そのあたりの確認方法についてもいずれ書いていきたいと思っている。