はじめに
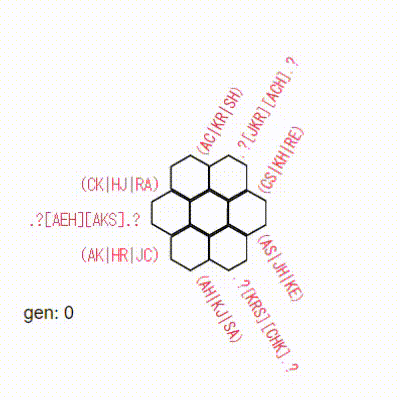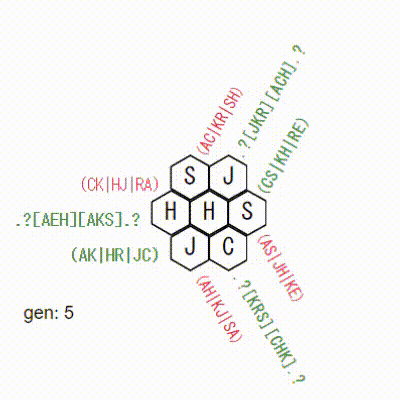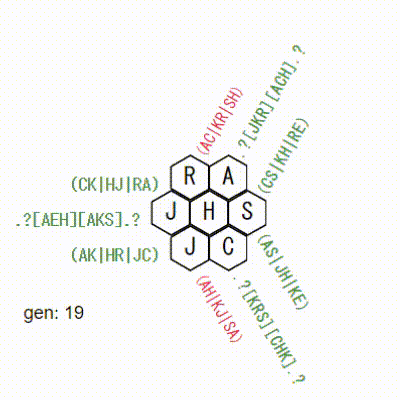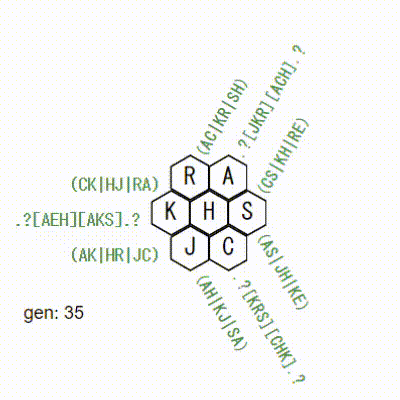
1週間ほど前、社内のチャットで、こんなクロスワードパズルがあるよ!とリンクが流れてきました。
なんじゃ、これは! おもしろそうすぎる!
さっそく、午後を半休にして、というわけにはいかなかったので、夜にがんばってみました。
やってみるとわかると思いますが、解いているときの感覚は、通常のクロスワードパズルと違って、お絵かきロジック(ノノグラム)や、マインスイーパーをやってるような感じでした。
結局夜にあまり時間が取れず、2晩かけて解いたのですが、ふと、こんなの、遺伝的アルゴリズムとかで推測させれば楽勝じゃね? という考えが浮かび、試してみました。
設計方針
得意なPythonで書き直そうかとも思ったのですが、画面でうにょうにょ動く方が楽しそうなので、元のソースを改造してみることにします。
遺伝的アルゴリズムとは
Wikipediaによると、
- あらかじめ N 個の個体が入る集合を二つ用意する。以下、この二つの集合を「現世代」、「次世代」と呼ぶことにする。
- 現世代に N 個の個体をランダムに生成する。
- 評価関数により、現世代の各個体の適応度をそれぞれ計算する。
- ある確率で次の3つの動作のどれかを行い、その結果を次世代に保存する。
- 個体を二つ選択(選択方法は後述)して交叉(後述)を行う。
- 個体を一つ選択して突然変異(後述)を行う。
- 個体を一つ選択してそのままコピーする。
- 次世代の個体数が N 個になるまで上記の動作を繰り返す。
- 次世代の個体数が N 個になったら次世代の内容を全て現世代に移す。
- 以降の動作を最大世代数 G 回まで繰り返し、最終的に「現世代」の中で最も適応度の高い個体を「解」として出力する。
ということだそうです。
仕様
まずは、この流れをベースに実装してみることにします。
途中経過が見えた方が楽しいので、「現世代」の中で最も適応度の高い個体を画面に表示することにします。
元ソースの研究
まず、キーボードの入力が前提になっているので、画面表示は自前で用意する必要がありそうです。
「評価関数」は成立している正規表現の数を数えればいいでしょう。
checkRules()という関数があるので、これを改造することにします。
実装
データの表示
こんな感じで実装してみました。
sizeはglobal変数のようでしたのでそのまま使います。
function draw(data) {
var rows = data.rows
var i, j, id, val;
for (i = 0; i < size; i += 1) {
for (j = 0; j < rowSize(i); j += 1) {
id = '#cell_' + i + '_' + j
val = (rows[i] && rows[i][j] || '')
if (val === '?') {
val = ''
}
$(id).val(val)
}
}
}
ランダムなデータの取得
こんかいは、アルファベット大文字だけのようなので、アルファベット大文字からなるランダムな盤面を返す関数を作成します。
function getRandomChar() {
return String.fromCharCode('A'.charCodeAt(0) + Math.random() * 26)
}
function getRandomData() {
var i, j
var data = { rows: [] }
for (i = 0; i < size; ++i) {
var row = []
for (j = 0; j < rowSize(i); ++j) {
row[j] = get_random_char()
}
data.rows[i] = row
}
return data
}
評価関数
これは、もともとある、checkRules()を改造します。
user_dataというglobal変数しかチェック出来ない極悪仕様なので、引数にデータを取れるようにします。
また、常に、結果の画面表示を変更してしまうので、制御できるようにします。
function checkRules(data=user_data, show=true) {
var ii;
var debug = [];
var match_num = 0;
function check(str, axis, idx) {
var rule = board_data[axis][idx];
var regex = new RegExp(rule);
var match = str.match(regex);
var ret;
if (match && match[0] === str) {
if (show) {
$('#rule_' + axis + '_' + idx).removeClass('nomatch');
$('#rule_' + axis + '_' + idx).addClass('match');
}
ret = 1;
} else {
if (show) {
$('#rule_' + axis + '_' + idx).removeClass('match');
$('#rule_' + axis + '_' + idx).addClass('nomatch');
}
ret = 0;
}
debug.push(axis + idx + ': ' + str + (match ? ' (match)' : ''));
return ret
}
for (ii = 0; ii < size; ++ii) {
var str = '';
for (jj = 0; jj < rowSize(ii); ++jj) {
str += data.rows[ii][jj];
}
match_num += check(str, 'y', ii);
str = '';
for (jj = 0; jj < size; ++jj) {
var i = jj;
var j = ii;
if (jj > mid) {
j -= (jj - mid);
}
if (data.rows[i][j] !== undefined) {
str += data.rows[i][j];
}
}
str = strReverse(str);
match_num += check(str, 'x', ii);
str = '';
for (jj = 0; jj < size; ++jj) {
var i = jj;
var j = ii;
if (jj < mid) {
j -= (mid - jj);
}
if (data.rows[i][j] !== undefined) {
str += data.rows[i][j];
}
}
match_num += check(str, 'z', ii);
}
$('#debug').html(debug.join('<br/>'));
return match_num
}
テスト
試しに動かしてみます。
data = getRandomData()
draw(data)
console.log(checkRules(data, true))
consoleには4が出力されました。
いい感じです。
N個のランダムな初期データを作成
現世代のデータN個を作成します。
データuser_dataとそれぞれの適応度matchを持つ配列を作成します。
それをsolveMainに渡して、そちらで判定、描画、次世代の計算をおこなうことにします。
const N = 200
function solve() {
var user_datas = []
for (var i = 0; i < N; i++) {
data = getRandomData()
user_datas.push({ user_data: data, match: checkRules(data, false) })
}
solveMain(user_datas)
}
描画と判定、次世代への繰り返し
ループで回したいところですが、ループで回してもブラウザが描画してくれませんので、setTimeout()を使ってG世代まで、または、解が見つかるまで繰り返します。
最も適応度の高いもののみを描画します。
次世代のデータはgetNextGen()で取得することにします。
function getBestData(user_datas) {
var best_data
var best_match = 0
for (var data of user_datas) {
if (data.match > best_match) {
best_match = data.match
best_data = data.user_data
}
}
return { user_data: best_data, match: best_match }
}
const G = 50
var g = 1
function solveMain(user_datas) {
finish = false
best = getBestData(user_datas)
$("#gen").text(g)
draw(best.user_data)
checkRules(best.user_data, true)
if (best.match == size * 3) {
console.log("solved!")
finish = true
}
if (g < G && !finish) {
g += 1
next_user_datas = getNextGen(user_datas)
window.setTimeout(() => solveMain(next_user_datas), 300);
} else {
console.log(g)
$("#gen").val(g)
}
}
次世代のデータの作成
次世代の要素として、適応度の高いものを高い確率で使うために、「ルーレット選択」を利用します。
簡単に言えば、たわしの部分が大きく、パジェロの部分が小さくなっている、アレです。たわしの適応度が高い場合、そのようになります。
getNextGenでは、ルーレットを作成し、データがN個になるまで遺伝子組み換えなどを繰り返します。
遺伝子組み換えはgetNextDataでおこないます。
function getNextGen(user_datas) {
var best_data
var best_match = 0
var next_user_datas = []
// Make a roulette (The more match has the more win)
var roulette = []
user_datas.forEach(arg => {
for (var i = 1; i <= arg.match; i++) {
roulette.push(arg.user_data)
}
})
for (var n = 0; n < N;) {
for (var new_data of getNextData(roulette)) {
match = checkRules(new_data, false)
next_user_datas.push({ user_data: new_data, match: match })
n += 1
if (n >= N) break
}
}
return next_user_datas
}
遺伝子組み換え
確率により、二点交叉、一様交叉、突然変異、ただのコピーをおこないます。
二点交叉は、端の方が変わりにくいので、終端と先端をつなぐようにしてみました。
const mutation_rate = 0.3;
const two_point_crossover_rate = 0.3;
const uniform_crossover_rate = 0.3;
const copy_rate = 1.0 - mutation_rate - two_point_crossover_rate - uniform_crossover_rate;
function deep_copy(o) {
return JSON.parse(JSON.stringify(o))
}
function swap(data1, data2, i, j) {
tmp = data1.rows[i][j]
data1.rows[i][j] = data2.rows[i][j]
data2.rows[i][j] = tmp
}
function getNextData(roulette) {
var ret = []
var rand = Math.random()
var new_data, new_data2
if (rand < copy_rate) {
// Copy
new_data = deep_copy(roulette[Math.floor(Math.random() * roulette.length)])
// do nothing
ret.push(new_data)
} else if (rand - copy_rate < mutation_rate) {
// Mutation
new_data = deep_copy(roulette[Math.floor(Math.random() * roulette.length)])
var swap_num = Math.floor(Math.random() * size)
for (i = 1; i <= swap_num; i++) {
i1 = Math.floor(Math.random() * size)
j1 = Math.floor(Math.random() * rowSize(i1))
new_data.rows[i1][j1] = getRandomChar()
}
ret.push(new_data)
} else {
tmp = roulette[Math.floor(Math.random() * roulette.length)]
new_data = deep_copy(tmp)
do {
tmp2 = roulette[Math.floor(Math.random() * roulette.length)]
} while (tmp2 == tmp)
new_data2 = deep_copy(tmp2)
if (rand - copy_rate - mutation_rate < uniform_crossover_rate) {
// Uniform Crossover
for (i = 0; i < size; i++) {
for (j = 0; j < rowSize(i); j++) {
if (Math.random() < 0.5) {
swap(new_data, new_data2, i, j)
}
}
}
} else {
// Two Point Crossover
i1 = Math.floor(Math.random() * size)
j1 = Math.floor(Math.random() * rowSize(i1))
i2 = Math.floor(Math.random() * size)
j2 = Math.floor(Math.random() * rowSize(i2))
if (i1 == i2) {
if (j1 <= j2) {
for (j = j1; j <= j2; j++) {
swap(new_data, new_data2, i1, j)
}
} else {
for (j = j1; j < rowSize(i1); j++) {
swap(new_data, new_data2, i1, j)
}
for (i = i1 + 1; i < size; i++) {
for (j = 0; j < rowSize(i); j++) {
swap(new_data, new_data2, i, j)
}
}
for (j = j2; j >= 0; j--) {
swap(new_data, new_data2, i1, j)
}
for (i = i1 - 1; i >= 0; i--) {
for (j = 0; j < rowSize(i); j++) {
swap(new_data, new_data2, i, j)
}
}
}
} if (i1 <= i2) {
for (j = j1; j < rowSize(i1); j++) {
swap(new_data, new_data2, i1, j)
}
for (i = i1 + 1; i < i2; i++) {
for (j = 0; j < rowSize(i); j++) {
swap(new_data, new_data2, i, j)
}
}
for (j = j2; j >= 0; j--) {
swap(new_data, new_data2, i2, j)
}
} else {
for (j = j1; j < rowSize(i1); j++) {
swap(new_data, new_data2, i1, j)
}
for (i = i1 + 1; i < size; i++) {
for (j = 0; j < rowSize(i); j++) {
swap(new_data, new_data2, i, j)
}
}
for (j = j2; j >= 0; j--) {
swap(new_data, new_data2, i2, j)
}
for (i = i2 - 1; i >= 0; i--) {
for (j = 0; j < rowSize(i); j++) {
swap(new_data, new_data2, i, j)
}
}
}
}
ret.push(new_data)
ret.push(new_data2)
}
return ret
}
動作確認
3x3で確認
元のソースに、3x3のデータも入ってたので、これで試してみます。
おーーー!
なかなかいい感じです。
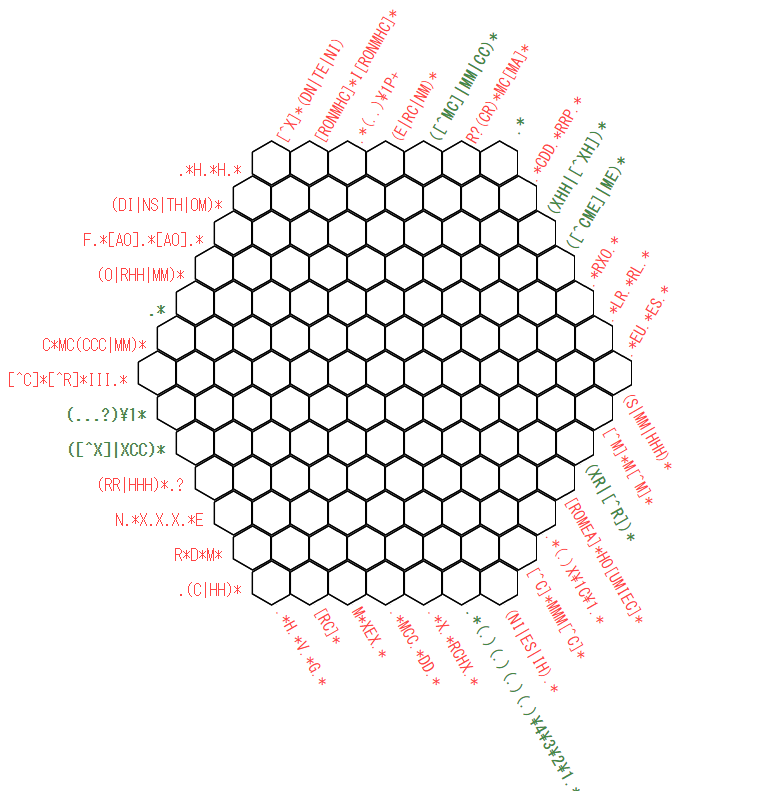
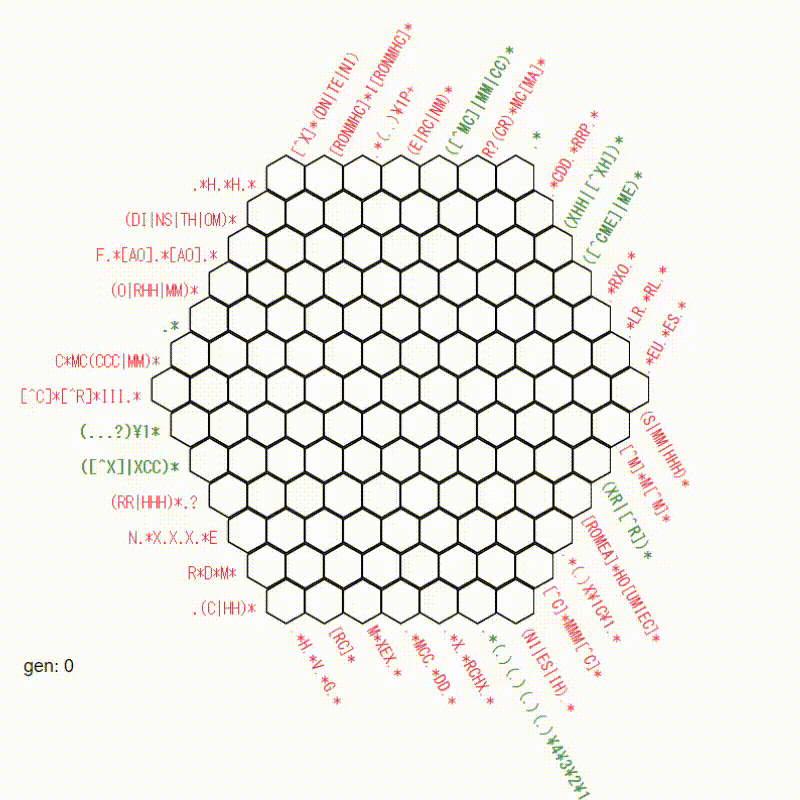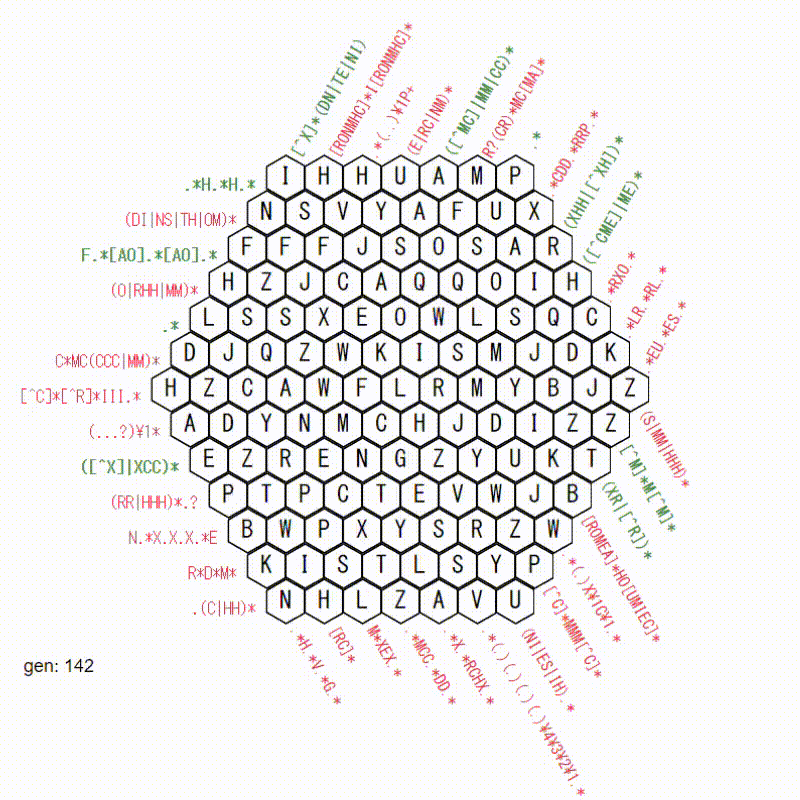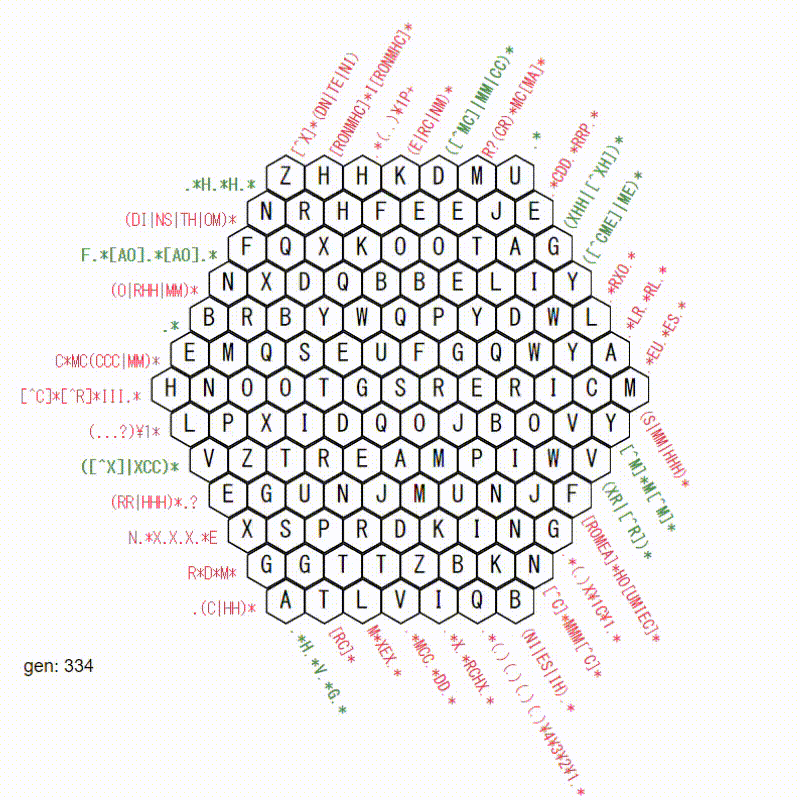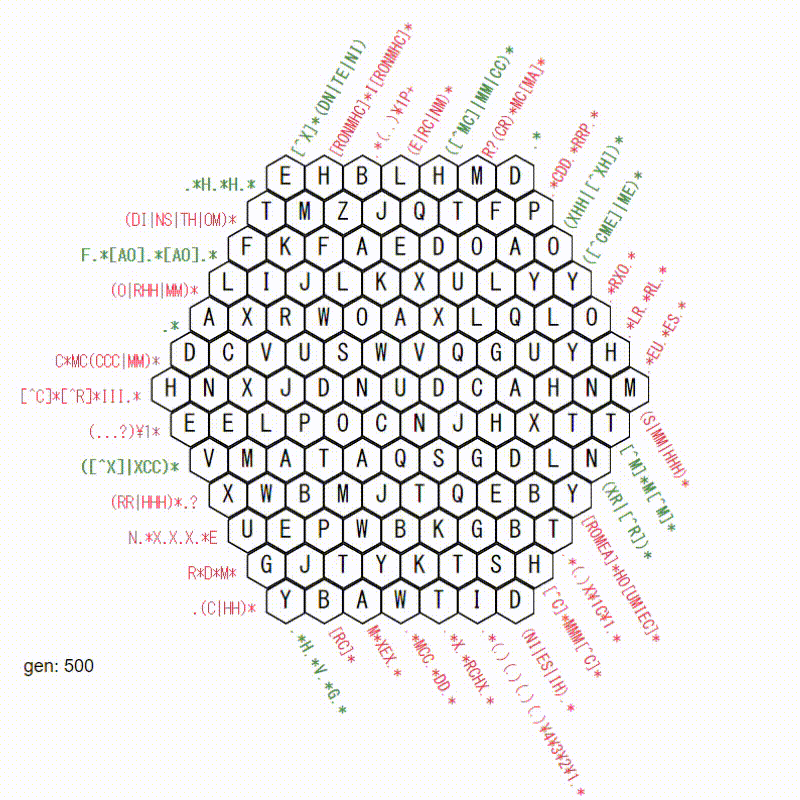
13x13で確認
おー!すげぇ!なんかかっこいいです!
でも、あまり、解けている感じがしません。
世代が足りないのでしょうか。
50000世代目です。
だいぶ進みましたが、この後続けてもほとんど進展がありませんでした。
考察
なんとなく眺めていて感じた感想なのですが、どうも、.*や([^X]|XCC)*の何でもマッチする系とは相性が悪いようです。
今回作成した評価関数は、単純に成立する正規表現の数なので、例えば、([^X]|XCC)*の場合、AAAAAAAAAAAは適応度が1で、XCAAAAAAAAAの適応度は0になります。
せっかく、XCCができるかも知れないチャンスが生かされないということです。
また、[RC]*のような特定の文字のみ許す系も、特定の文字以外が1文字でもあれば評価は0です。つまり、この[RC]*が成立するのは、奇跡的にRかCの文字のみで構成されたときだけで、おそらく、この行が成立することはないでしょう。
正規表現の評価関数が、0/1ではなく、0.3くらい合ってる、というようなふうにできれば、いい線行くのではないかと思うのですが、それは簡単ではなさそうですし、そこまでできるなら、別の方法で答えが出せそうな気がします。
結論
頑張って、自力で解きましょう。
おまけ
今回のコードは
においてあります。
feature/solverブランチです。