LoginSignup
0
1

More than 3 years have passed since last update.

@hinaqiita

再帰処理で求める順列(nPr)【JavaScript】

Posted at

この記事について

プログラミングクイズを解くにあたり、再帰処理を使うとスラッと解けそうな気がする問題がいくつかありました。
そのなかでも「順列」は特に使いこなせるようになりたかったので調べて記事にまとめました。

以下の説明をしています。
- 順列とは何か
- 順列を出力するサンプルコード

以下は説明しません。
- 公式 $nPr=\frac{n!}{(n-r)!}$を使った順列総パターン数の計算方法

順列とは何か

そもそも順列ってなんでしょうか？

結論

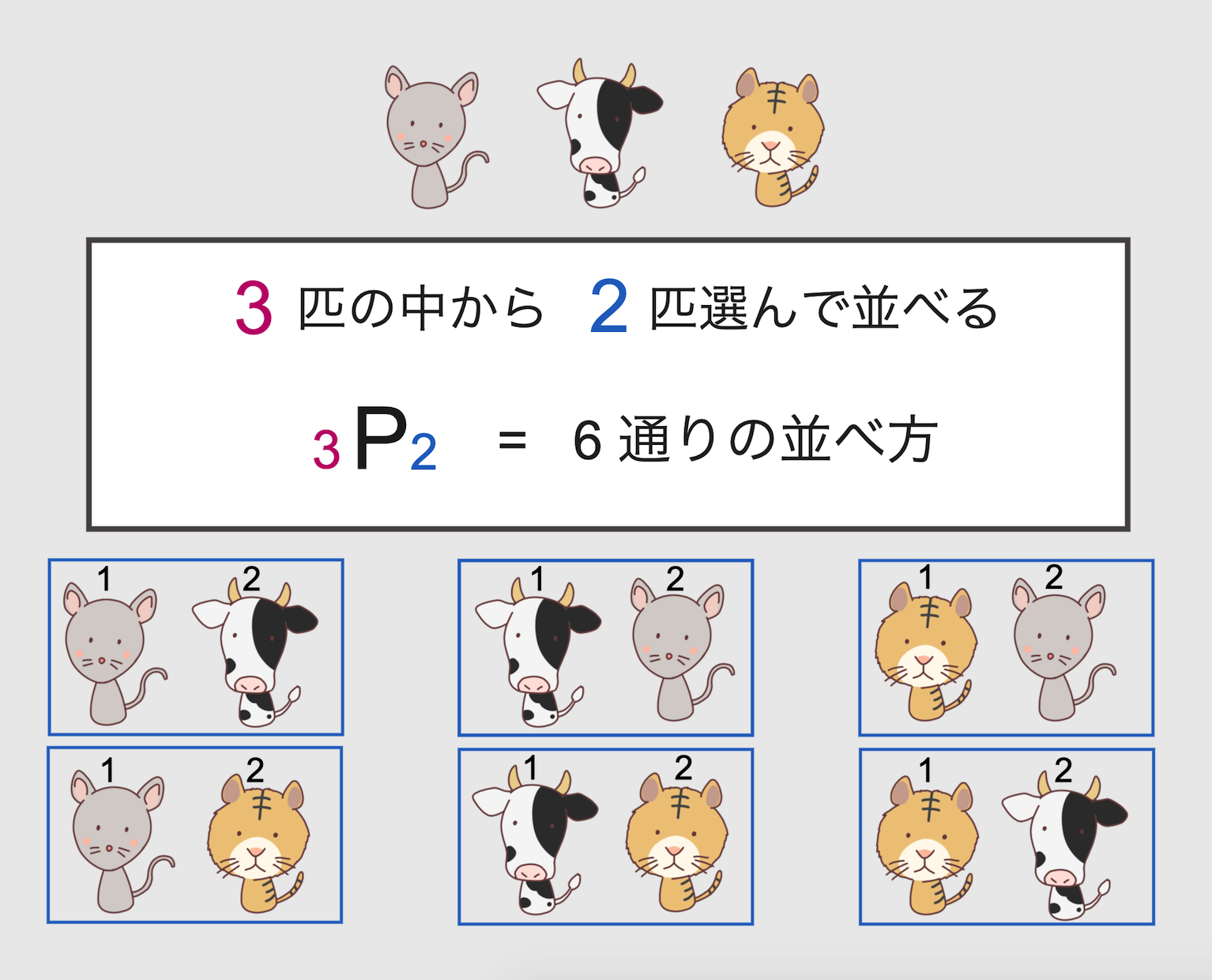
順列(nPr)は、「n個の物の中からr個を取り出して一列に並べたもの」です。
nPrのPはpermutationの略で、そのまま「順列」という意味です。
例えば3匹の動物から2匹を取り出して一列に並べると、以下のような順列になります。

image

組み合わせ(nCr)との違いに注意

注意しなければならないのは、「1:ねずみ」「2:うし」と「1:うし」「2:ねずみ」は異なるものだという点です。
image
上記を「同じ」とみなす考え方は「組み合わせ(nCr)」といいます。
この2つはよく混同されますが別物なので気をつけてください。

nCrについては以下の記事がわかりやすかったです。
５分で分かる！確率統計「nCr」の計算方法

順列の洗い出し方

どのように並べれば順列を取得のか、例を上げて解説します。

4匹から２匹選ぶ例

4匹の動物ねずみ🐭、うし🐮、とら🐯、うさぎ🐰から2匹選んで並べるとき、以下の手順で並べるとパターンを網羅できます。

  1. [ねずみ]と[それ以外の動物]を並べる
  2. [うし]と[それ以外の動物]を並べる
  3. [とら]と[それ以外の動物]を並べる
  4. [うさぎ]と[それ以外の動物]を並べる
  🐭
  - [ねずみ]と
      - [うし]
      - [とら]
      - [うさぎ]

  🐮
  - [うし]と
      - [ねずみ]
      - [とら]
      - [うさぎ]

  🐯
  - [とら]と
      - [ねずみ]
      - [うし]
      - [うさぎ]

  🐰
  - [うさぎ]と
      - [ねずみ]
      - [うし]
      - [とら]

4匹の動物それぞれに3匹の動物を並べています。
よって 4 × 3 = 12 通り の順列ができあがります。

4匹から3匹選ぶ例

4匹の動物ねずみ🐭、うし🐮、とら🐯、うさぎ🐰から3匹選んで並べるとき、以下の手順で並べるとパターンを網羅できます。

  1. [ねずみ]と[うし]と[それ以外の動物]を並べる
  2. [ねずみ]と[とら]と[それ以外の動物]を並べる
  3. [ねずみ]と[うさぎ]]と[それ以外の動物]を並べる
  4. [うし]と[ねずみ]と[それ以外の動物]を並べる
  5. [うし]と[とら]と[それ以外の動物]を並べる
  6. [うし]と[うさぎ]]と[それ以外の動物]を並べる
  7. [とら]と[ねずみ]と[それ以外の動物]を並べる
  8. [とら]と[うし]と[それ以外の動物]を並べる
  9. [とら]と[うさぎ]]と[それ以外の動物]を並べる
  10. [うさぎ]と[ねずみ]と[それ以外の動物]を並べる
  11. [うさぎ]と[うし]と[それ以外の動物]を並べる
  12. [うさぎ]と[とら]と[それ以外の動物]を並べる

  🐭
  - [ねずみ]と
      - [うし]と
          - [とら]
          - [うさぎ]
      - [とら]と
          - [うし]
          - [うさぎ]
      - [うさぎ]と
          - [うし]
          - [とら]

  🐮
  - [うし]と
      - [ねずみ]と
          - [とら]
          - [うさぎ]
      - [とら]と
          - [ねずみ]
          - [うさぎ]
      - [うさぎ]と
          - [ねずみ]
          - [とら]

  🐯
  - [とら]と
      - [ねずみ]と
          - [うし]
          - [うさぎ]
      - [うし]と
          - [ねずみ]
          - [うさぎ]
      - [うさぎ]と
          - [ねずみ]
          - [うし]

  🐰
  - [うさぎ]と
      - [ねずみ]と
          - [うし]
          - [とら]
      - [うし]と
          - [ねずみ]
          - [とら]
      - [とら]と
          - [ねずみ]
          - [うし]

4匹の動物それぞれに3匹の動物を並べています。
さらにそこから2匹を並べたパターンを列挙しています。
よって 4 × 3 × 2 = 24通り の順列ができあがります。

余談: 順列のパターンの総数

上記で説明したように、順列は並べる数(r)が増えれば増えるほどパターンの総数も増えていきます。
その総数を知りたい場合は「nのr回分の階乗」を求めればOKです。
階乗はその数から1ずつ引いた数を掛け合わせた数のことで、たとえば5の階乗は5×4×3×2×1です。

例：

  • 5種類から3つ選んで並べる(5の3回分の階乗)
    $ _{5}P_{3} = 5\times 4 \times3 = 60$ 通り

  • 6種類から4つ選んで並べる(6の4回分の階乗)
    $ _{6}P_{4} = 6\times 5 \times 4 \times 3 = 360$ 通り

  • 5種類から1つ選んで並べる(5の1回分の階乗)
    $ _{5}P_{1} = 5$ 通り

  • 3種類から3つ選んで並べる(3の3回分の階乗)
    $ _{3}P_{3} = 3\times 2 \times1 = 6$ 通り

上記のイメージを持っておくとコードの理解がしやすくなると思います👍
きちんとした公式($nPr=\frac{n!}{(n-r)!}$)を使って求める方法もありますが、これはコードの説明から話が逸れすぎるので割愛します。

参考:【高校数学】1から分かる順列と組み合わせの違い

サンプルコード

紹介した順列の羅列方法を元にコードを書いてみます。

関数

const getPermutation = (types, r) => {
  const result = [];

  // r が 1 の場合
  if (r === 1) {
    for (let i = 0; i < types.length; i++) {
      result[i] = [types[i]];
    }
    return result;
  }

  // r が 2以上の場合
  for (let i = 0; i < types.length; i++) {
    const parts = types.slice(0);
    parts.splice(i, 1)[0];
    const row = getPermutation(parts, r - 1);
    for (let j = 0; j < row.length; j++) {
      result.push([types[i]].concat(row[j]));
    }
  }

  return result;
};

参考: 順列・組み合わせ のサンプルコード JS [permutation] [combination]

4匹から１匹選ぶ例

実行結果

const result = getPermutation(['ねずみ', 'うし', 'とら', 'うさぎ'], 1);
console.log(JSON.stringify(result));

// 実行結果
// [
//   ['ねずみ'],
//   ['うし'],
//   ['とら'],
//   ['うさぎ']
// ]

解説

rが1だった場合は、以下の条件分岐に当てはまり、ただただ要素を1つずつ別の配列にしたものが返却されます。

  // r が 1 の場合
  if (r === 1) {
    for (let i = 0; i < types.length; i++) {
      result[i] = [types[i]];
    }
    return result;
  }

4匹から2匹選ぶ例

実行結果


// 実行
const result = getPermutation(['ねずみ', 'うし', 'とら', 'うさぎ'], 2);
console.log(result);

// 実行結果
// [
//   ['ねずみ', 'うし'],
//   ['ねずみ', 'とら'],
//   ['ねずみ', 'うさぎ'],
//   ['うし', 'ねずみ'],
//   ['うし', 'とら'],
//   ['うし', 'うさぎ'],
//   ['とら', 'ねずみ'],
//   ['とら', 'うし'],
//   ['とら', 'うさぎ'],
//   ['うさぎ', 'ねずみ'],
//   ['うさぎ', 'うし'],
//   ['うさぎ', 'とら'],
// ];

解説

関数が実行されると、まず['ねずみ','うし','とら','うさぎ']を順に処理するためのループを開始します。
(以降はループ1回目(i = 0)の前提で説明します。)

 for (let i = 0; i < n.length; i++) {

次に、「parts」という変数に [ 'うし', 'とら', 'うさぎ' ]を代入しています。

const parts = types.slice(0);
parts.splice(i, 1)[0];
// [ 'うし', 'とら', 'うさぎ' ]

slice(0)は値コピーのためにつけています。 (参考:JavaScriptで配列のコピー（値渡し）)
splice()は要素を一部削除する関数です。 (参考:MDN -Array.prototype.splice()-)

次に、自分自身の関数を実行します。 

const row = getPermutation(parts, r - 1);

このように、自分で自分自身の関数を呼ぶことを再帰呼び出しといいます。
(参考:再帰関数を学ぶと、どんな世界が広がるか)

再起呼び出しをする際の引数は以下の通りです。

第一引数 : parts( ['うし', 'とら', 'うさぎ'])
第二引数 : 1

処理の流れは前章で説明した通りで、r = 1 だった場合の処理が実行されています。
戻り値は以下のようになっています。

// lowの中身
// [
//   ['うし'],
//   ['とら'],
//   ['うさぎ']
// ]

最後に、concat()で[ねずみ]と['うし'],['とら'],['うさぎ']をそれぞれ結合し、result配列に格納しています。

for (let j = 0; j < row.length; j++) {
      result.push([types[i]].concat(row[j]));
    }

ここでresult配列に格納された値は以下の通りです。

[
  [ 'ねずみ', 'うし' ],
  [ 'ねずみ', 'とら' ],
  [ 'ねずみ', 'うさぎ' ],
]

上記の動きを、ネズミ以外の動物にも順次繰り返すことで結果が得られます。

4匹から3匹選ぶ例

実行結果


const result = getPermutation(['ねずみ', 'うし', 'とら', 'うさぎ'], 3);
console.log(result);

// 実行結果
// [
//   ['ねずみ', 'うし', 'とら'],
//   ['ねずみ', 'うし', 'うさぎ'],
//   ['ねずみ', 'とら', 'うし'],
//   ['ねずみ', 'とら', 'うさぎ'],
//   ['ねずみ', 'うさぎ', 'うし'],
//   ['ねずみ', 'うさぎ', 'とら'],
//   ['うし', 'ねずみ', 'とら'],
//   ['うし', 'ねずみ', 'うさぎ'],
//   ['うし', 'とら', 'ねずみ'],
//   ['うし', 'とら', 'うさぎ'],
//   ['うし', 'うさぎ', 'ねずみ'],
//   ['うし', 'うさぎ', 'とら'],
//   ['とら', 'ねずみ', 'うし'],
//   ['とら', 'ねずみ', 'うさぎ'],
//   ['とら', 'うし', 'ねずみ'],
//   ['とら', 'うし', 'うさぎ'],
//   ['とら', 'うさぎ', 'ねずみ'],
//   ['とら', 'うさぎ', 'うし'],
//   ['うさぎ', 'ねずみ', 'うし'],
//   ['うさぎ', 'ねずみ', 'とら'],
//   ['うさぎ', 'うし', 'ねずみ'],
//   ['うさぎ', 'うし', 'とら'],
//   ['うさぎ', 'とら', 'ねずみ'],
//   ['うさぎ', 'とら', 'うし'],
// ];

解説

最初の処理は$_{４}P_{2}$の処理と同じです。
まず['ねずみ','うし','とら','うさぎ']を対象にするループを開始し、parts配列([ 'うし', 'とら', 'うさぎ' ])を作成します。

  for (let i = 0; i < n.length; i++) {
    const parts = types.slice(0);
    parts.splice(i, 1)[0];
    // [ 'うし', 'とら', 'うさぎ' ]

次に、自分自身の関数を実行します。 

const row = getPermutation(parts, r - 1);

再起呼び出しをする際の引数は以下の通りです。

第一引数 : parts( ['うし','とら', 'うさぎ'])
第二引数 : 2

今回は第二引数が2になるので、 r が 2 以上の場合に該当し、さらに再帰処理を行います。

'うし'と'それ以外' などのペアになる順列を取得します。

  for (let i = 0; i < n.length; i++) {
    const parts = types.slice(0);
    parts.splice(i, 1)[0];
    // [ 'とら', 'うさぎ' ]

const row = getPermutation(['とら', 'うさぎ'], 1);

rowには以下の結果が格納されています。

//[
//   [ 'うし', 'とら' ],
//   [ 'うし', 'うさぎ' ],
//   [ 'とら', 'うし' ],
//   [ 'とら', 'うさぎ' ],
//   [ 'うさぎ', 'うし' ],
//   [ 'うさぎ', 'とら' ]
// ]

最後に、['ねずみ']と、row配列の要素['うし']['とら']などを結合し、result配列に格納しています。

  for (let i = 0; i < n.length; i++) {
    const parts = types.slice(0);
    parts.splice(i, 1)[0];
    // 実行結果
    // [
    //   ['ねずみ', 'うし', 'とら'],
    //   ['ねずみ', 'うし', 'うさぎ'],
    //   ['ねずみ', 'とら', 'うし'],

    // ...(略)

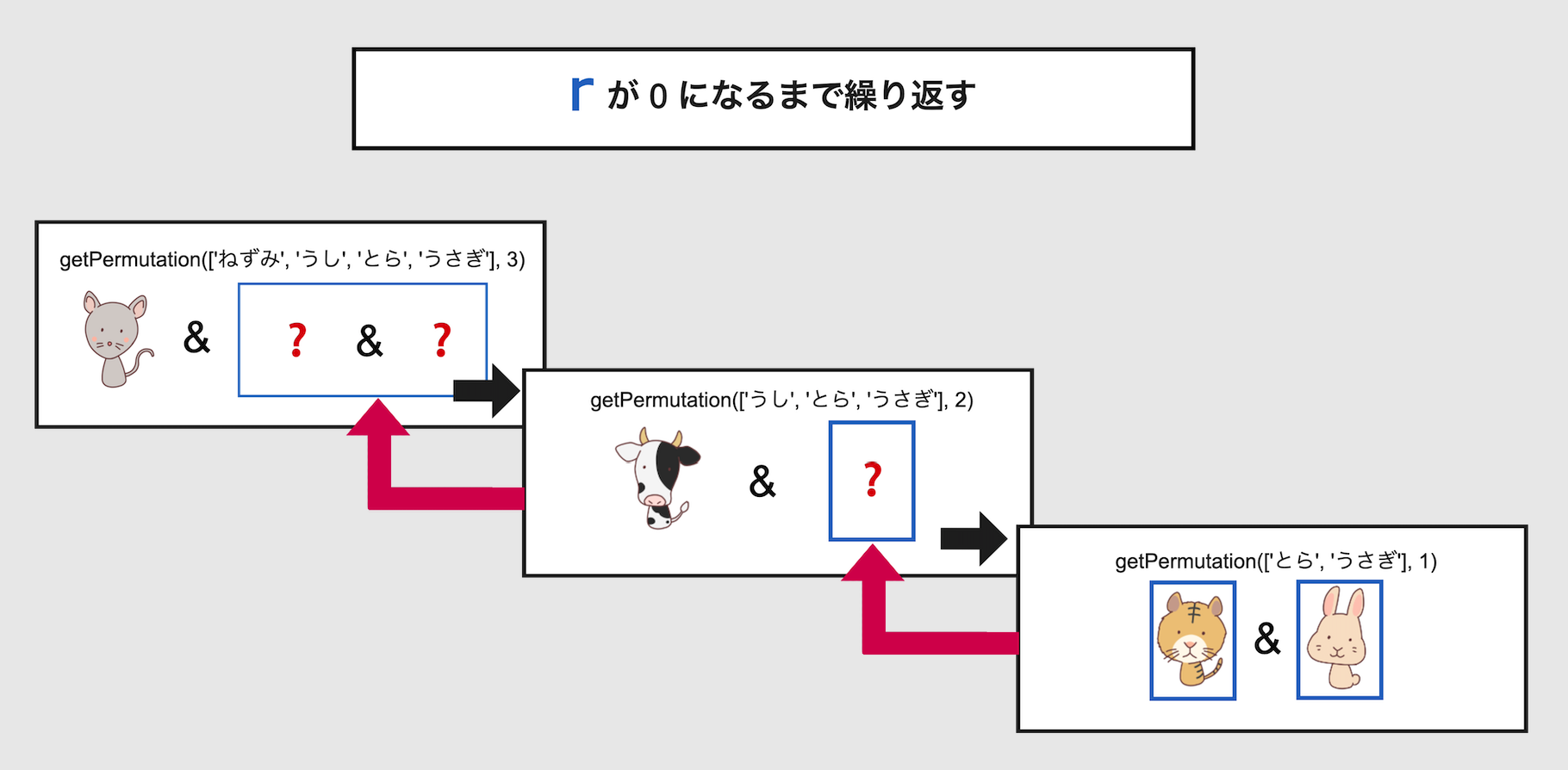
上記サイクルを終えて'ねずみ'から始まる全ての順列を洗い出したら、以降同じ手順で'うし'や'とら'から始まる順列を取得します。
このようにr === 1になるまで何度も繰り返し再帰呼び出しを行うことで、最終的に必要な配列を出力することができます。

image

まとめ

順列(nPr)は、「n個の物の中からr個を取り出して一列に並べたもの」です。
r回数分再帰処理を繰り返すことで答えを導くことができます。

再帰処理を使えば、倍々に選択肢が増えていくような処理(チェスのコマを置く場所や移動経路の探索など)が書けるようになると思います。
例題はたくさんあるので、他の処理もいつか記事にしてみたいと思います。

ちなみにとてもかわいい動物の素材はこちらにお借りしました。
イラストレイン

0
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
1