~8080Labsが考案した新スコア「PPS」は、相関係数を凌駕できるだろうか?!~
はじめに
「相関係数よ、安らかに眠れ」
変数間の関係性を示す新たな尺度PPS(Predictive Power Score:予測パワースコア)を考案した8080Labs のブログ記事は、このようなちょっと過激なタイトルがつけられています。

※これらはすべて相関係数=0
相関は、2変数の線形関係を示すものなので、線形関係以外の関係は存在しても表現することができません。
例えば、𝑦 = 𝑥² の相関係数は0です。相関はAとB、BとAの関係が同じとなる対照関係を相手にしています。𝑥が2なら𝑦は4、𝑥が-2でもなら𝑦は4となりますが、𝑦が4のときは𝑥が2か-2かはわかりません。現実世界はこのような非対称性がよくありますし、2変数の関係は数値同士だけではなく、カテゴリー型もあります。
このPPS(Predictive Power Score)は、線形だろうと非線形だろうと、ガウスだろうと、カテゴリー型だろうと、これらにとらわれない尺度として、8080Labs が考案したスコアだそうです。
相関係数とPPSの比較
| 相関 | PPS | |
|---|---|---|
| 扱える2変数 | 線形のみ | 線形•非線形とも |
| 2変数の傾向とスコアの関係 | 正弦波、二次曲線などはr≒0 | 非対称関係も扱える |
| データ型 | 数値同士のみ | カテゴリーデータも可 |
| スコアの解釈 | 相関 = 線形関係 | PPS = パターン発見 |
| スコアの値 | -1〜+1 | 0〜1 |
| スコアの意味 | 1なら完全な正の相関、-1なら負の相関、 0なら無相関 | 1なら𝑥で完璧に𝑦を予測でき、0なら𝑥で𝑦を予測する力が全くない |
PPSのメリット
先の通り、二次関係𝑦=𝑥² の相関係数は0となりますが、PPS は𝑥から𝑦が0.67 、𝑦から𝑥のPPSは0となります。相関では関係の有無がわからない非線形関係もPPSなら検出することができます。
ブログでは、kaggle「タイタニック生存予測」での比較例も示されていました。
『「中程度の負の相関(-0.55)」があったTicketPriceとClass(客室クラス)のPPSをみると「TicketPriceはClass (客室クラス)の強い予測因子(0.9PPS)、Class (客室クラス)はTicketPriceを0.2PPSで予測するだけ」という関係にあった』とあります。
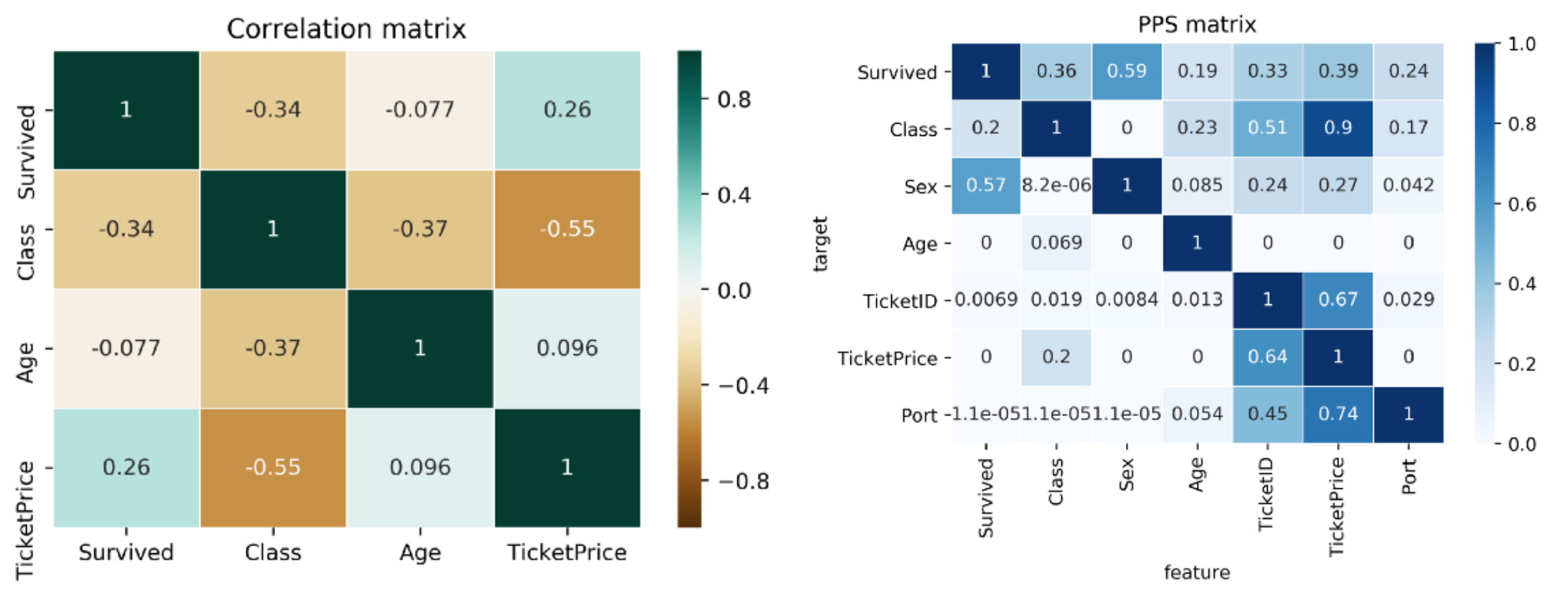
※Datasetのカラム名 Fare⇒TicketPrice,Ticket⇒TicketID,Pclass⇒Class,Embarked⇒Portに変えてる?
TicketPriceでClass (客室クラス)は予測できるが、あるClass (客室クラス)の人がTicketにいくら支払ったかの予測はむつかしいという非線形関係の存在がわかります。
また、PPSのスコアからはSurvived(生存)の最良の一変量予測因子はSex(性別)であることもわかります。カテゴリーデータが扱えない相関係数行列では、そもそもこれに気がつけません。
TicketPriceがSurvived(生存)に対して予測力を持っている(PPS 0.39)ことも示されていました。相関係数は0.26でしかありませんので、(これに気がつけるのは)ありがたいですね。
PPSが紹介された記事
https://qiita.com/ssl_ds_sps/items/ba218ebd641eafa7927b
こちらの記事では、特徴量選択時の使用法について、簡潔に述べられています。
- PPSの低い特徴量を変数重要度のように除外する
- PPSのマトリクスを作って、特徴量間のPPSが高い者同士は、相関マトリクスで多重共線性を見出すのと同様に、冗長な情報を互いに含んでいる特徴量である可能性が高いので、重要なものだけ残す
- カテゴリカル変数と数値変数の双方に対してPPSが算出されるので、様々な変数間の非線形性を含めた関係性を見出すのに便利
とてもわかりやすく、参考になりますね。
予測力スコア(PPS)の算出方法
PPSは、
- データ型や水準数によって、二つの特徴量間もしくは特徴量とターゲット変数間の関係性を回帰問題もしくは分類問題のいずれかに判別し、
- 欠損値の除外、カテゴリ特徴量のone-hotエンコード、ターゲットのlabelエンコード等の前処理を行ったうえで
- クロスバリデーションによる決定木(ターゲットが数値の場合、Mean Absolute Error(MAE)を、ターゲットがカテゴリーの場合、重み付きF1を計算)モデルを構築し算出。。。とのこと。
なかなか、手が混んだスコアなんだなということはわかります。
実行条件など
・Google colabで実行
・Kaggleのタイタニックデータで実行
■ タイタニックのデータセットについて
以下サイト(Kaggle)の「train.csv」を使わせていただいた。
**タイタニックデータセットの項目と内容**
|項目|内容|
|:-----------|:------------------|
|PassengerId|乗客ユニークID|
|Survived|生存フラグ(0=死亡,1=生存)|
|Pclass|チケットクラス(1=上級,2=中級,3=下級)|
|Name|乗客名|
|Sex|性別(male=男性,female=女性)|
|Age|年齢|
|SibSp|同乗している兄弟,配偶者の数|
|parch|同乗している親,子供の数|
|ticket|チケット番号|
|fare|料金|
|cabin|客室番号|
|Embarked|出港地(C=Cherbourg,Q=Queenstown,S=Southampton)|
PPSスコアを求めてみよう!
1. ライブラリのインストールおよびインポート
以前もある記事で描いたが、使用するライブラリをいちいち検討するのは面倒なので、基本以下としています。乱暴ですいません。
pip install -U ppscore
# 日本語化
pip install japanize-matplotlib
# Import required libraries
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
sns.set(font="IPAexGothic")
from scipy.stats import norm
import ppscore as pps
import warnings
warnings.simplefilter('ignore')
2. データの読み込み
df = pd.read_csv('train.csv')
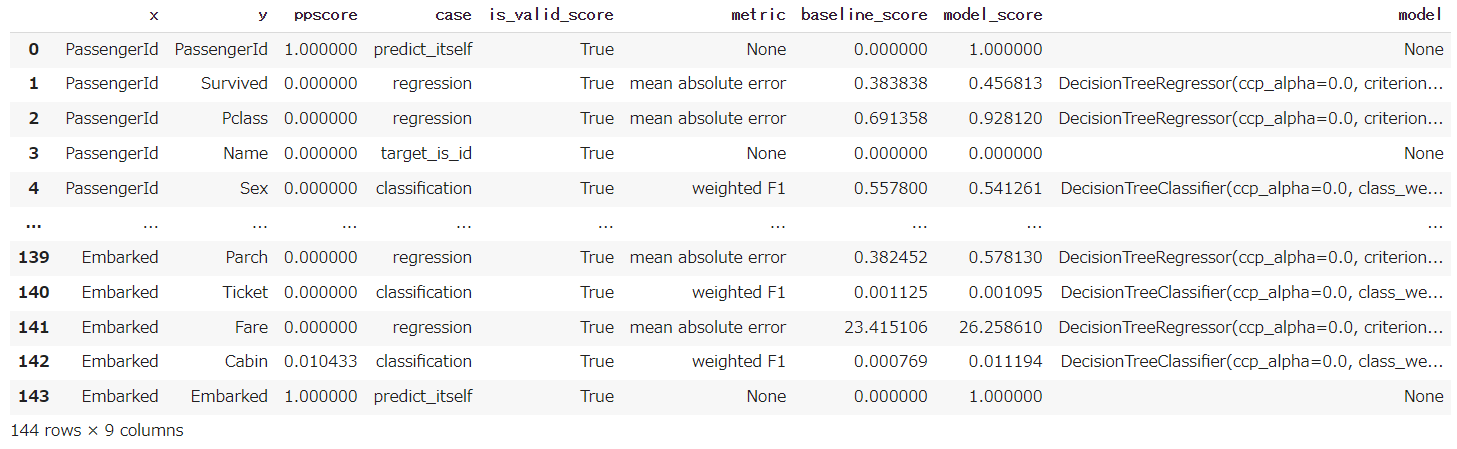
df.head()
3. PPSスコア計算
pps.matrix(df)
4. PPSマトリクス
plt.figure(figsize=(18,6))
sns.set(font_scale = 1.5)
plt.title('PPS:Predictive Power Score (x = feature, y = target)', fontsize = 22)
matrix_df = pps.matrix(df)[['x', 'y', 'ppscore']].pivot(columns='x', index='y', values='ppscore')
sns.heatmap(matrix_df, vmin=0, vmax=1, cmap="Blues", linewidths=0.5, annot=True)
plt.show()
PPSとの付き合い方
8080Labs は、ブログ記事でPPS の限界を知っておく必要があると述べられています。
- PPSスコアの計算は相関関係(マトリックス)に比べて遅いです。(※私は気になるレベルではないと思いました)
- PPSスコアは、発見された関係について何も教えてくれないので、相関関係のように簡単に解釈することはできません。PPS はパターンを見つけるのに適しています。相関は見つけた線形関係を伝えるのに適しています。
- PPSスコアを把握することに価値はありますが、異なるターゲット変数のスコアは、異なる評価基準で計算されたものなので、厳密に数学的に比較することはできません。
- PPSはターゲットに対する特徴間の相互作用効果は検出できません。
最後に
PPSは、特徴量エンジニアリングにおいていつもと異なる示唆を与えてくれそうです。
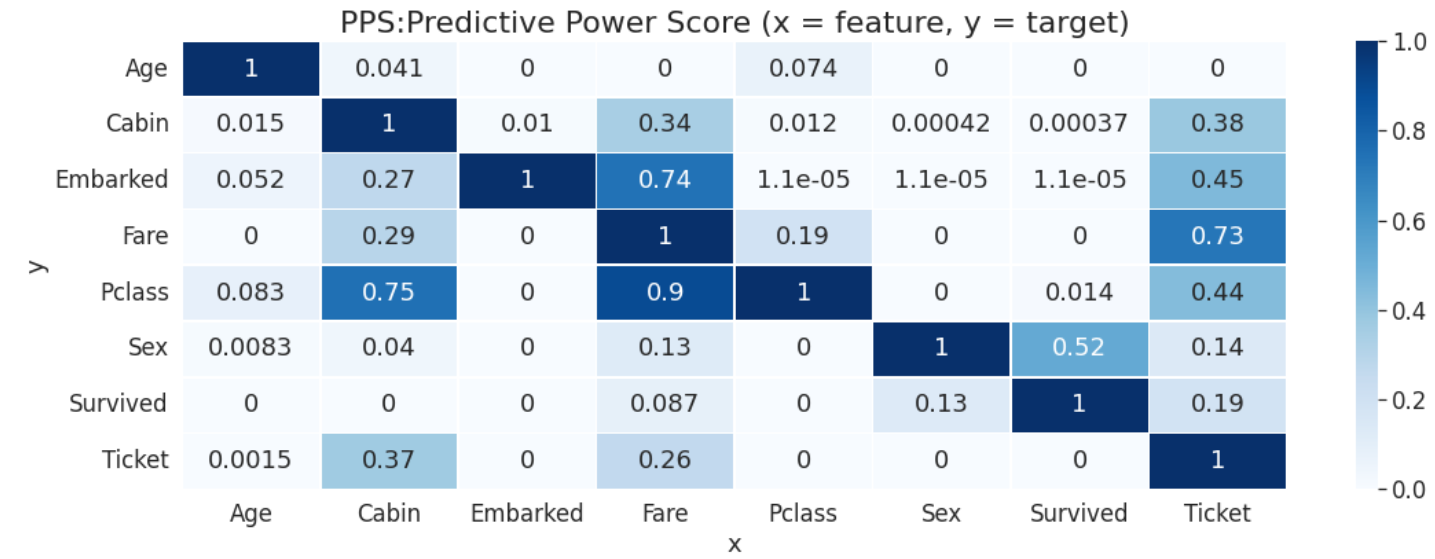
マトリクスは読み方に注意が必要です。
x≂feature, y=targetです。x(特徴量)がy(ターゲット)に対してどれだけ予測力を持っているか?です。
添付のマトリクスならば、Ticket(x)はSurvived(y)に対して予測力を持っている(PPS 0.19)んだなという具合です。ちなみにSurvivedからTicketのPPSは0となっています。
チケットで生死は予測できる可能性があるが、生死からチケットは予測できない・・・たしかにその通りですね。
これは現実の感覚にとても近いスコアですね。
参考サイト