特徴量選択
この記事では、今年4月に公開されたPredictive Power Scoreという特徴量選択に活用できる指標と、それを実装したライブラリppscoreを紹介します。
さて、予測モデルを作成する際に、使用する特徴量や説明変数を選ぶことを特徴量選択といい、
- 予測に無関係なデータのノイズを減らす
- 計算コストを削減するために、冗長なデータを減らす
といった目的で行われます。
特徴量選択の手法は大きく以下のように分類することができます。Predictive Power ScoreはWrapper手法に相当しますが、実装内容からFilter手法の良さも兼ね備えています。
| 手法 | 概要 | 特徴 |
|---|---|---|
| Filter | データ自体の統計量等を計算し、閾値を設けて足切りすることで、特徴量を選択する | 相対的に最も計算コストが少なく、大規模なデータセットに適している |
| Embedded | 正則化のように、特徴量選択とモデル構築を同時に行う | Filter手法とWrapper手法の中間的な特徴を持つ |
| Wrapper | モデル構築と特徴量選択を繰り返し、試行することで予測に有用な特徴量を選択する | 実際にモデル構築を行っているため、予測に有用な特徴量選択を精緻に行うことができる反面、計算コストが高い |
Predictive Power Score
主な特徴
Predictive Power Score(以降PPSとする)はドイツに拠点を持つ8080Labsというソフトウェア会社が開発した考え方です。
EDA等でよく用いられるピアソン相関係数の相関マトリックスを使った分析と似たような形で使え、より汎用的に使用できるような指標を作れないだろうかというのモチベーションのもと開発されているようです。
PPSに以下のような特徴があります。
- カテゴリカル変数と数値変数のいずれに対しても適用できる
- PPSは0と1の間の値を持ち、0とは、xという特徴量で、yというターゲットを予測する力が全くないということに対応し、1は、xで完璧にyを予測できることに対応する
- ピアソン相関係数等はxとyの線形な関係を前提にしているが、PPSは非線形な関係に対しても評価はできる
- ただし、変数間の相互作用に関しては考慮されていない
- 後述するが、シンプルなモデルを構築しているため、計算速度はFilter手法のものより劣る反面、普通のWrapper手法(変数重要度やPermutation Importanceのような手法)よりは早い
- PPSの値は0~1の間だが、異なるターゲットに対して計算されたPPS同士の比較に数学上の厳密な意味はない
- PPSの算出にはMAEとF1を使った場合でしか実装されておらず、他の指標を試したい場合は自分で実装が必要になる
PPSの算出方法
- データの型や水準数(カーディナリティ)によって、二つの特徴量間もしくは特徴量とターゲット変数間の関係性を回帰問題もしくは分類問題のいずれかに判別する
- 欠損値の除外、カテゴリ特徴量のone-hotエンコード、ターゲットのlabelエンコード等前処理を行う
- 回帰問題と分類問題それぞれで、異なるPPSの定義式に従い、PPSの計算をする
2.で言及されている定義式は、下表の通りです。
| タスク | PPSの計算定義式 |
|---|---|
| 回帰 | PPS = 1 - (MAE_model / MAE_naive) |
| 分類 | PPS = (F1_model - F1_naive) / (1 - F1_naive) |
MAE_modelとMAE_naiveはそれぞれxを用いてyを予測したときのMAE、yの中央値を予測した際のMAEです。_naiveを計算している理由は、PPSを0~1の範囲に収めるために正規化する基準を設定するためです。
F1_naiveの場合は、最も頻出のクラスに対しての重み付きF1を算出しております。
ここで疑問に思われた方もいると思いますが、「予測」はどのように行っているのでしょうか。
Wrapper手法に相当しますが、実装内容からFilter手法の良さも兼ね備えています
前述のように、特徴量選択の文脈ではPPSの算出はWrapper手法に分類することができるのですが、予測は決定木モデルを構築して行っており、モデルを介在したスコアだからです。(スコア計算時に交差検証でモデルを構築している)ただ、PPSを一回算出してしまえば、絞り込んだ特徴量セットをより複雑なモデルに入れることも可能なのでFilter手法的に使うことも可能です。というのも、開発者がうたっているように、スコア計算時に一変数のシンプルな決定木モデルを構築している上に、決定木自体SVM、GBDT、NNなどに比べて計算速度が速いからです。
また、決定木であれば、非線形な関係も捉えられて、予測性能が比較的にロバストであることも使用されている理由です。
特徴量選択時の使用法
- 変数重要度のようにPPSの低い特徴量を除外する
- 特徴量間でPPSのマトリックスを作って、特徴量間のPPSが高い者同士は、相関マトリックスで多重共線性を見出すのと同様に、冗長な情報を互いに含んでいる特徴量である可能性が高いので、重要なものだけ残す
- より精緻に特徴量選択を行う場合には、Greedy(貪欲に)に変数を増やしていったり、減らしていったり、変数の増減をランダムに入れたりして試行することも考えられる
特徴量選択以外の使い方
- データからパターンを見出す
- データリーケージの検出
1.カテゴリカル変数と数値変数の双方に対してPPSが算出されるので、様々な変数間の非線形性を含めた関係性を見出すのに便利です。
2.著しくPPSがほかの特徴量に比べて高い場合には、予測時に活用できない情報を多く含んでいるリーケージに寄与する特徴量である可能性を疑うことができます。
ライブラリーの紹介
インストール
pip install ppscore
インポートとスコアの計算
import ppscore as pps
pps.score(df, "feature_column", "target_column")
PPSマトリックスの出力
pps.matrix(df)
実際にデータに適用してみた
使用データと環境
Telco Customer Churnというインターネットサービスの利用顧客情報とその解約情報に関するデータセットです。
環境はKaggleのnotebookを使用します。

データセットページに「New Notebook」という青いボタンがあるので、それをクリックすればすぐにデータセットにアクセスできる形でノートブックが立ち上がります。
準備
インストールします。
!pip install ppscore
ライブラリインポートとデータの読み込みを行います。
import numpy as np
import pandas as pd
import ppscore as pps
import seaborn as sns
import matplotlib.pyplot as plt
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
PATH ='/kaggle/input/telco-customer-churn/WA_Fn-UseC_-Telco-Customer-Churn.csv'
df = pd.read_csv(f'{PATH}')
df.shape
列名を確認します。
list(df.columns)
Churnがターゲットです。
['customerID',
'gender',
'SeniorCitizen',
'Partner',
'Dependents',
'tenure',
'PhoneService',
'MultipleLines',
'InternetService',
'OnlineSecurity',
'OnlineBackup',
'DeviceProtection',
'TechSupport',
'StreamingTV',
'StreamingMovies',
'Contract',
'PaperlessBilling',
'PaymentMethod',
'MonthlyCharges',
'TotalCharges',
'Churn']
データタイプを確認します。
df.dtypes
customerID object
gender object
SeniorCitizen int64
Partner object
Dependents object
tenure int64
PhoneService object
MultipleLines object
InternetService object
OnlineSecurity object
OnlineBackup object
DeviceProtection object
TechSupport object
StreamingTV object
StreamingMovies object
Contract object
PaperlessBilling object
PaymentMethod object
MonthlyCharges float64
TotalCharges object
Churn object
dtype: object
PPSの計算
pps.score(df, 'InternetService', 'Churn')
結果は辞書形式で返されます。
{'x': 'InternetService',
'y': 'Churn',
'task': 'classification',
'ppscore': 1.625853361551631e-07,
'metric': 'weighted F1',
'baseline_score': 0.6235392486748098,
'model_score': 0.6235393098818076,
'model': DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='gini',
max_depth=None, max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort='deprecated',
random_state=None, splitter='best')}
PPSマトリックスの可視化
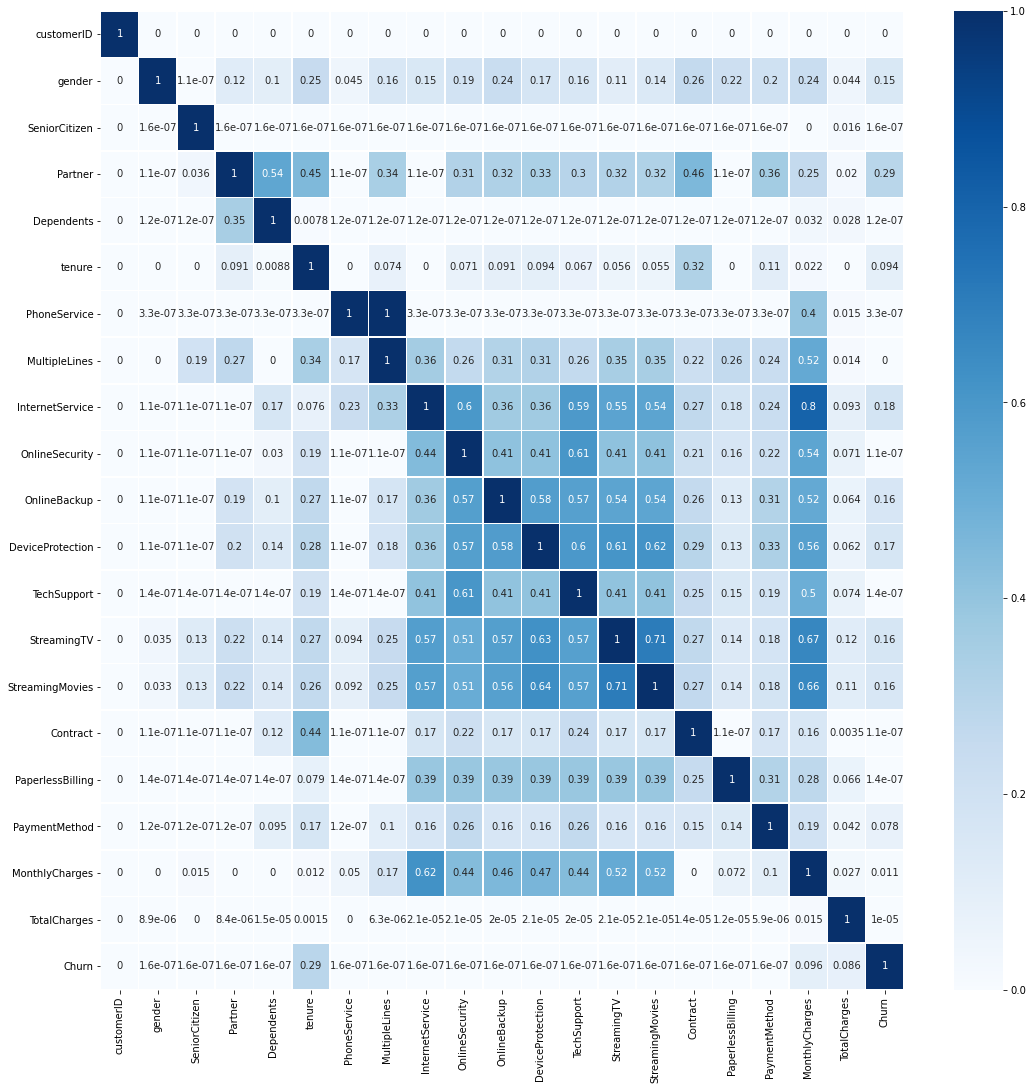
マトリックスを見ると、Churnの行では、ターゲットに対する各特徴量のPPSがヒートマップで表されており、特にtenure、MonthlyCharges、TotalChargesのPPSが大きくなっています。それぞれの意味は、サービス利用期間、月額利用料、累計利用料であり、解約と大きく関係のある特徴量となっています。
また、MonthlyChargesの行に注目すると、InternetServiceからStreamTVまでのPPSのコントラストが濃くなっています。これらの特徴量は上でデータ型を確認したように、カテゴリカル変数ですが、数値変数であるMonthlyChargesとの関係性を一緒に見ることができるのは便利ですね。解釈もしやすく、様々なインターネットサービスのオプション加入状況が利用料と強い関係性があることが確かめられます。
加えて、InternetServiceからStreamTVの特徴量間のPPSを見ますと、濃いコントラストになっており、類似した情報をお互いに持っていることが推察され、次元圧縮や次元削減を考慮できます。
なお、マトリックスの計算は(7043, 21)のデータフレームで1分55秒かかりました。決して早くはありませんが、万単位のデータであれば少し待てばよく、もっとデータ件数が増える場合にはサンプリングして傾向をつかむことも試してよいでしょう。
df_matrix = pps.matrix(df)
plt.figure(figsize=(18,18))
sns.heatmap(df_matrix, vmin=0, vmax=1, cmap="Blues", linewidths=0.5, annot=True)
plt.show()
最後に
ここまで、Predictive Power Score (PPS)について紹介してきました。
気軽にデータに適用でき、且つデータ間の関係性が簡単に可視化されるため、EDAでも特徴量選択でも使用できることがわかりました。ppscoreの実装ではMAEとF1をPPSの計算に使用していますが、PPSの概念を取り入れつつ、他の指標も試すこともできるでしょう。