前回に引き続き、Pythonを用いて、実数のみを用いた簡単な関係式をシミュレートすると不思議な結果が出てくること及び、虚数を使うとそれがうまく説明できるようなケースを紹介することで、より皆様に虚数に親しみを持ってもらおうと思います。
惑星の運動方程式
突然ですが、万有引力による惑星の運動方程式は以下のようなものになります。
\displaylines{
\vec{F} = m\vec{a} = -\frac{GMm}{r^3}\vec{r} \\
\vec{F}:力 \\
m:惑星の質量 \\
\vec{a}:惑星の加速度 \\
G:万有引力定数 \\
M:恒星の質量 \\
m:惑星の質量 \\
\vec{r}:惑星の位置 \\
r:\vec{r}の長さ}
解析的に解くには2回積分をする必要があり、かなりめんどくさいのですが、そこはPythonに任せて力任せにシミュレートすればなんともないです。また、仮定は可能な限り単純化します。$GM=1$となるような都合のいい恒星(質点)を考えます。すると以下のようになります。
\displaylines{
m\vec{a} = -m\frac{\vec{r}}{r^3} \\
\vec{a} = \frac{\vec{r}}{r^3} \\}
これをプログラムでシミュレートしていきます。
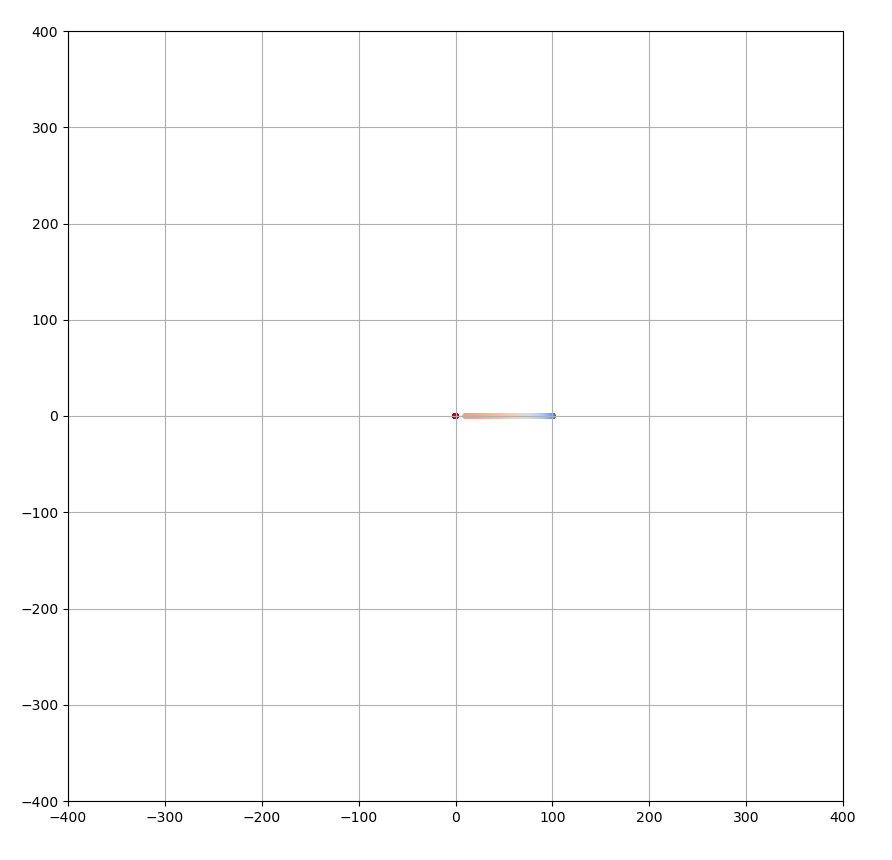
自由落下
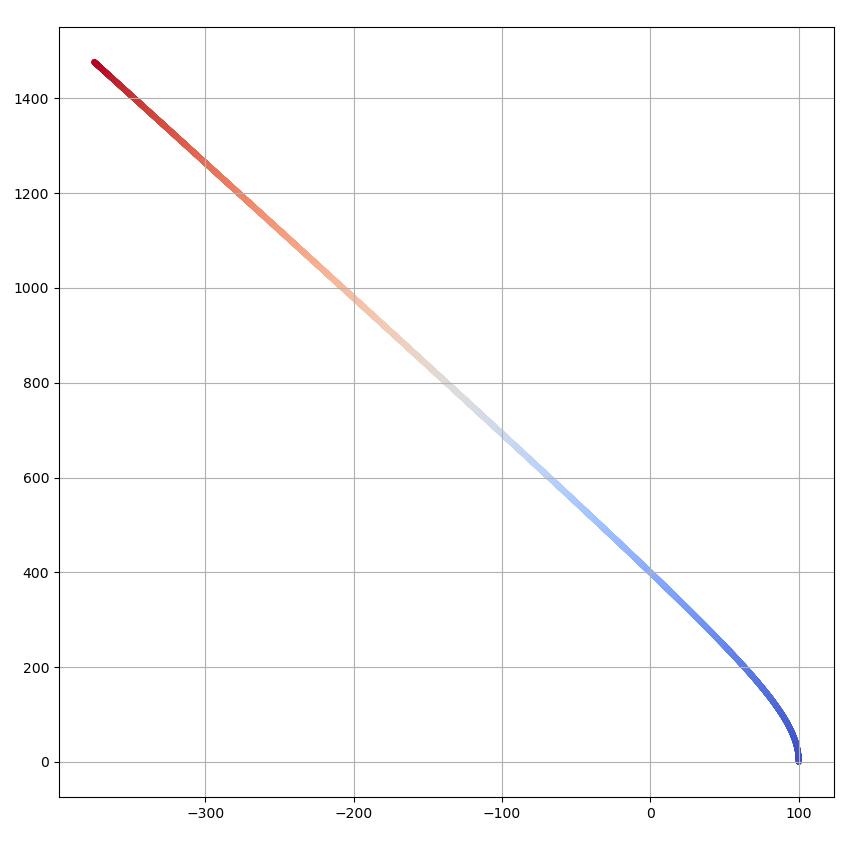
初期条件として、$\vec{r}=(100,0),\vec{v}=(0,0)$を考えます。恒星の中心から100mの位置にある惑星が、恒星に向かって自由落下していくようなイメージです。ソースコードは以下のようになります(import等は省略)。
size = 1500
x, y, vx, vy, ax, ay = np.zeros((6, size))
x[0] = 100
y[0] = 0
vx[0] = 0.0
vy[0] = 0.0
for i in range(size-1):
r = np.linalg.norm((x[i], y[i]))
if r < 10:
print("too close!")
break
ax[i] = -x[i]/r**3
ay[i] = -y[i]/r**3
vx[i+1] = vx[i] + ax[i]
vy[i+1] = vy[i] + ay[i]
x[i+1] = x[i] + vx[i]
y[i+1] = y[i] + vy[i]
plt.figure(figsize=(10, 10))
plt.scatter(x, y, s=10, c=range(size), cmap=cm.coolwarm)
plt.xlim(-400, 400)
plt.ylim(-400, 400)
plt.grid()
plt.show()
x,y,vx,vy,ax,ayがそれぞれ座標、速さ、加速度を表していて、運動方程式をシミュレートしています。rが0に近すぎる場合、計算結果がおかしくなってしまうので(現実世界でも、その前に地表に激突したり、電子の反発力に阻まれたりして、0に近い距離には近づけません)、ある閾値より小さくなった計算を打ち切ることにします。
結果は以下のようになります。
青がスタート位置、赤が終点になります。
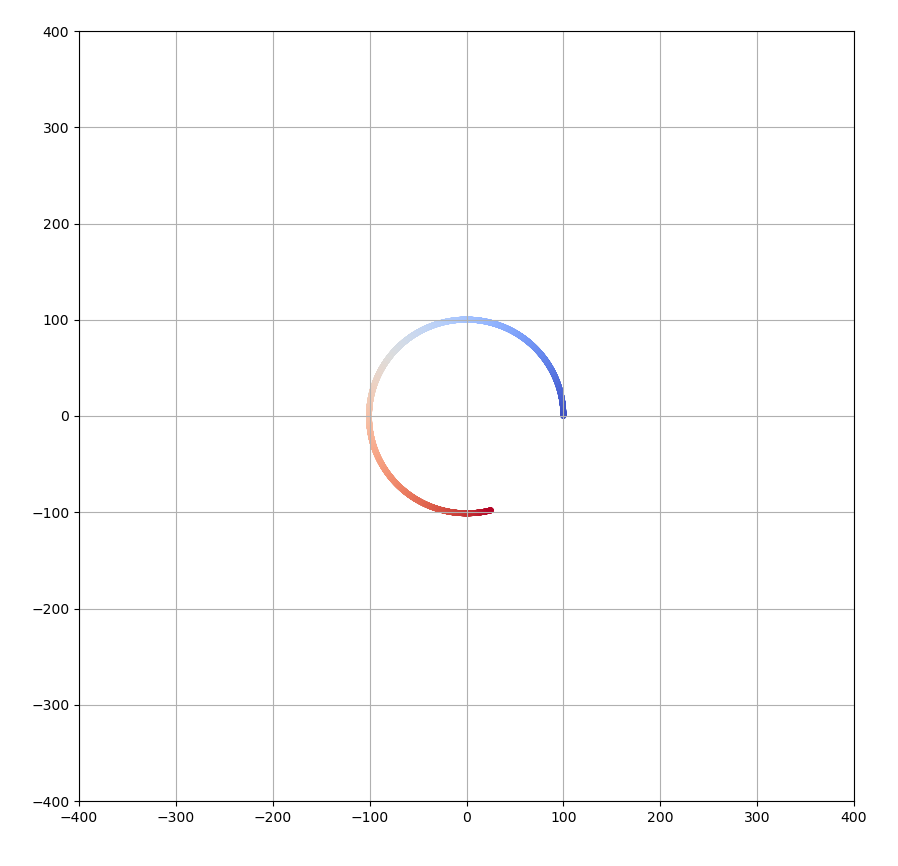
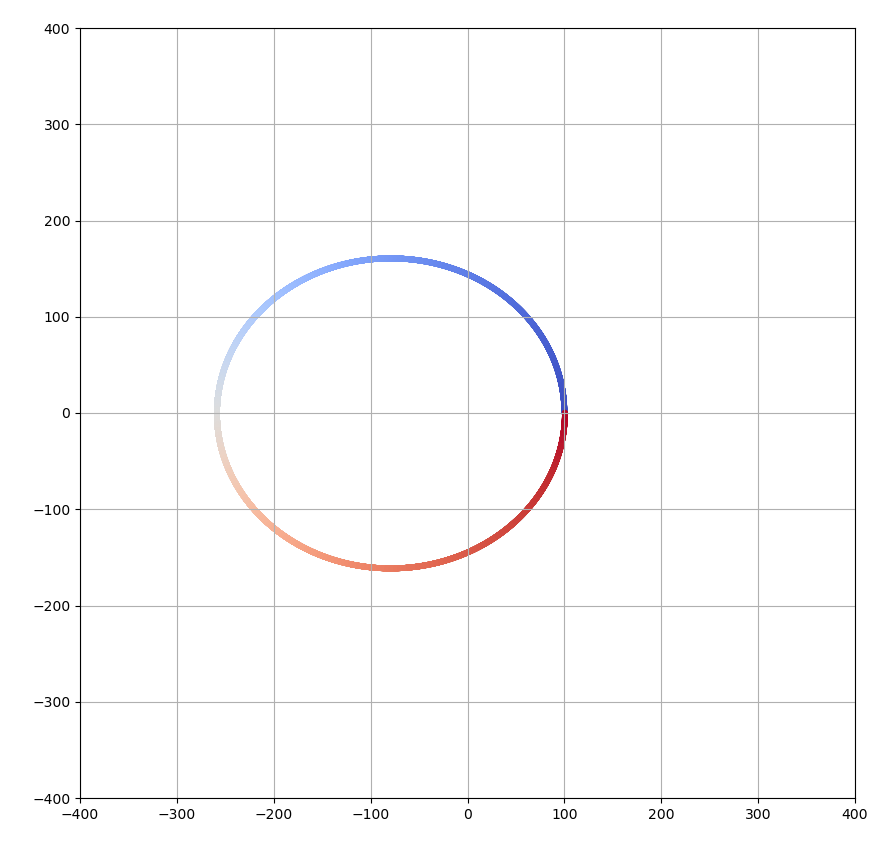
円軌道
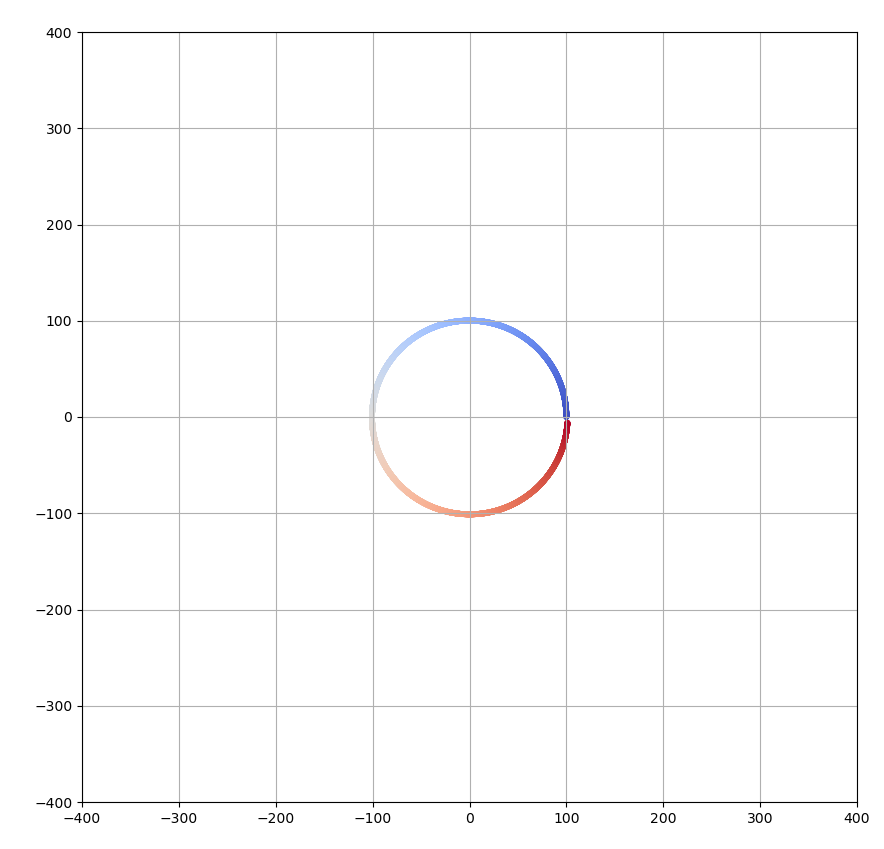
次に、グラフで言うと上向きに方向に初速度を加えます。うまく値を設定すると、真円の軌道に乗せることができます。vy[0]=0.1がそのような値となります。(sizeもうまく描画範囲になるように調整しています)
x, y, vx, vy, ax, ay = np.zeros((6, size))
x[0] = 100
y[0] = 0
vx[0] = 0.0
vy[0] = 0.1 # ここの部分
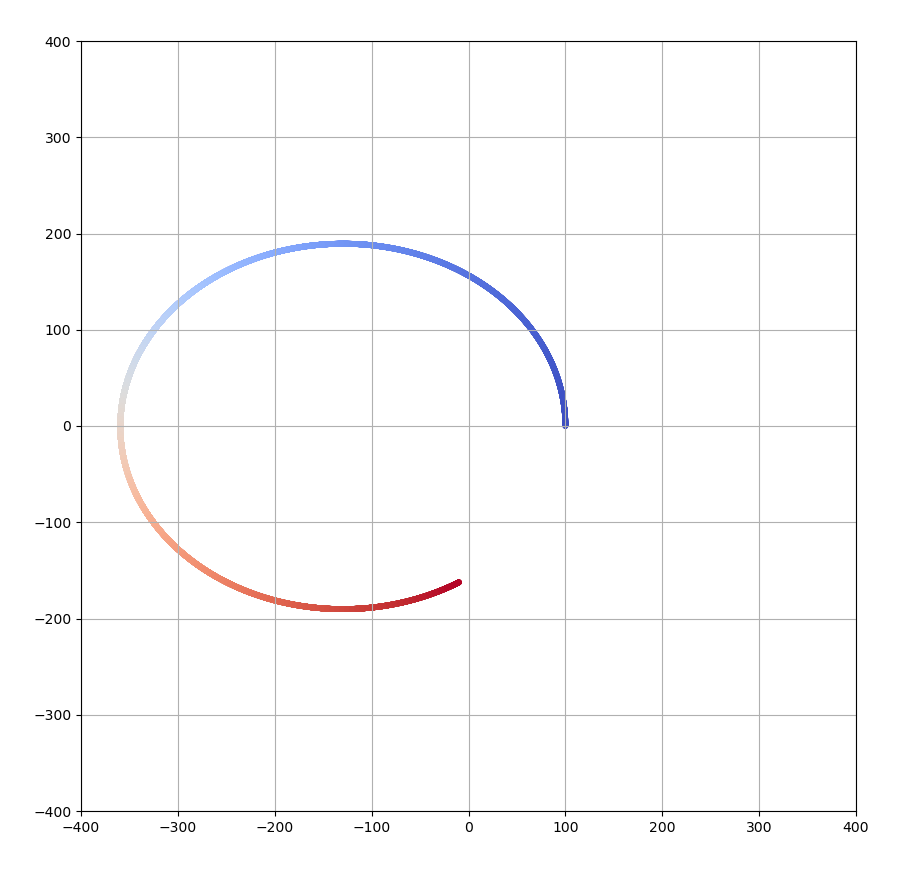
ちなみに、vy[0] = 0.125だと以下のような楕円になります。
円でなくなる
しかし、ある速度を超えると、円軌道ではなくなってしまいます。
vy[0] = 0.1414だと以下のような感じになります。
ネタバレをするとこれは放物線になります。
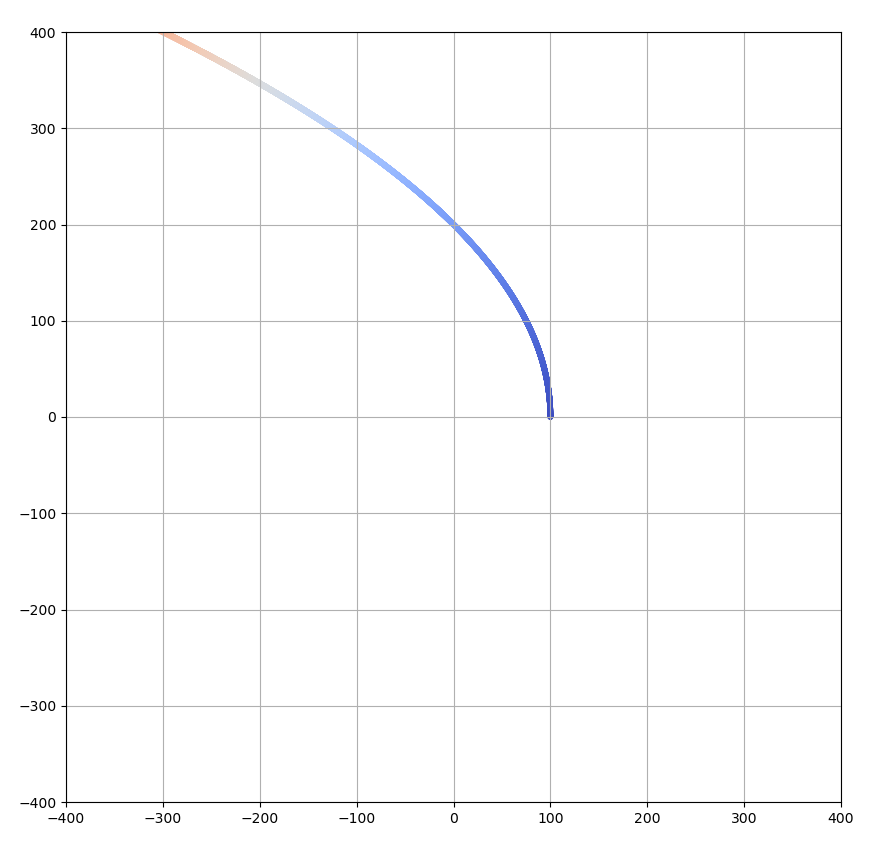
vy[0] = 0.2だと以下のような感じになります。(軌道の特徴を見やすくするため、グラフの中心と尺度を変えています)
明らかに双曲線ですね。
現実の世界の天体も、(おおまかに近似すれば)このように楕円軌道(惑星、衛星)や双曲線運動(彗星等はこれの場合もあります)を行うことが知られています。
楕円曲線のパラメータ
この挙動を定量的に解析するためには、先の運動方程式を解く必要がありますが、そのあたりは先人の知恵があるので、要点だけを拝借します。楕円軌道の各パラメータは以下のようになります。
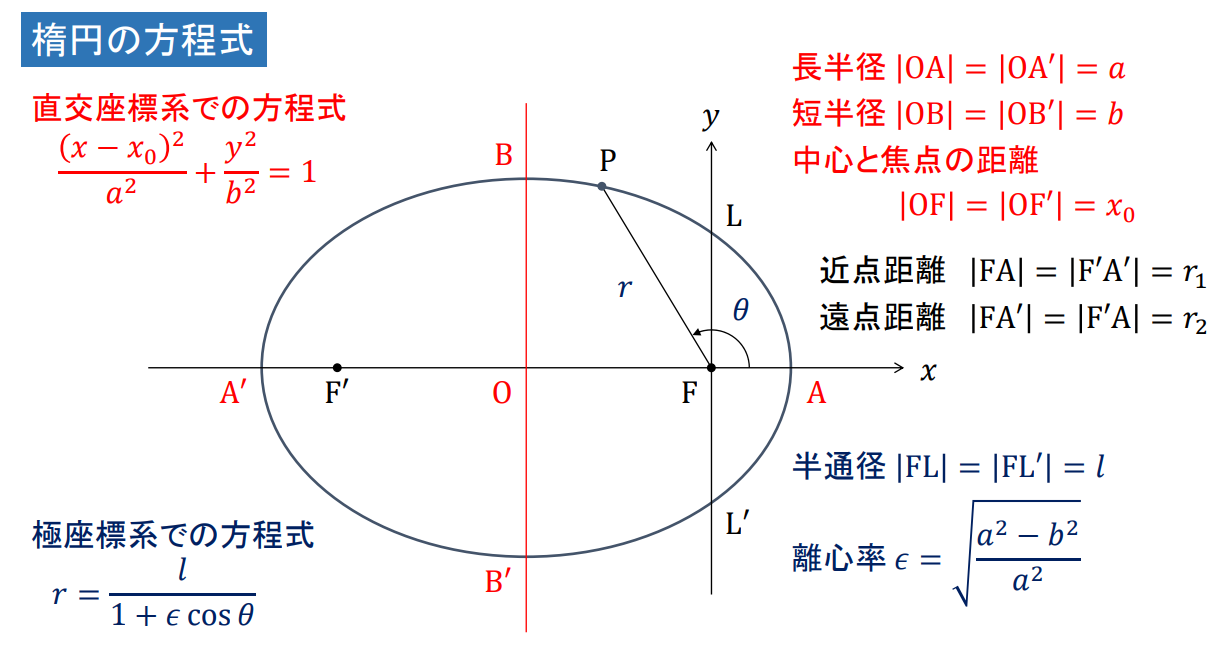
(https://www.eee.kagoshima-u.ac.jp/~watanabe-lab/misc/%E6%A5%95%E5%86%86%E3%81%A8%E5%B9%B3%E5%9D%87.pdf より引用)
半通経 $l$ は以下のように計算されます。(なお、以下のパラメータ群は、__恒星の質量$M$を都合のいい場合に設定し、垂直方向にのみ初速度ある場合に成り立つ特殊値__であることに注意してください)
l = r^2v^2
離心率$e$はどうなるでしょうか。これは計算が少しめんどくさいのですが、結論を述べると、
e=\sqrt{1+r^2v^4-2rv^2}
になります。要は、$v=\pm\frac{1}{\sqrt{r}}$の時に最小値0を取り、$v=\pm\sqrt{\frac{2}{r}}$の時に1となり、後は増え続けるだけになります。
離心率は、
- 0の時は真円に
- 1未満の時は楕円に
- 1の時に放物線に
- 1より大きい時は双曲線
になるので、シミュレーションの結果と一致していることがわかります。
余談になりますが、以下のケースは高校物理の範囲でも計算することができます。
- 真円...遠心力と重力が釣り合う時
\displaylines{
\frac{m}{r^2} = \frac{mv^2}{r} \\
v = \pm\frac{1}{\sqrt{r}}}
- 放物線...無限遠で運動エネルギー+位置エネルギーが0になる時
\displaylines{
0 = \frac{1}{2}mv^2 - \frac{m}{r} \\
v = \pm\sqrt{\frac{2}{r}}}
さて、話を戻して、楕円のパラメータをもう少し詳しく見てみます。
軌道長半径$a$は、
\displaylines{
a = \frac{l}{1-e^2} \\
=\frac{r^2v^2}{1-(1+r^2v^4-2rv^2)} \\
=\frac{r^2v^2}{2rv^2-r^2v^4} \\
=\frac{r}{2-rv^2}}
になります。
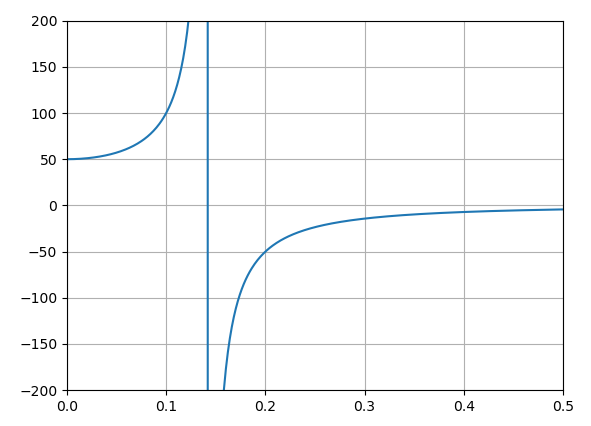
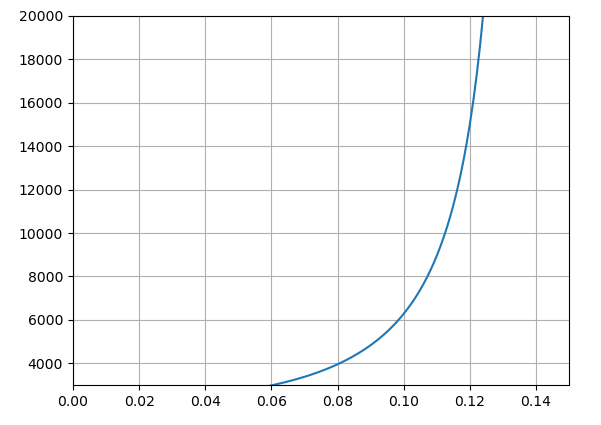
$a=f(v)$をグラフにするとこんな感じです。
vy[0]=0.1で半径100の真円になります。ちなみに、0.1以下の値だと、原点を「左側の」焦点とした楕円運動に、0.1以上だと、原点を「右側の」焦点とした楕円運動になります。軌道長半径は大きくなり続けていきますが、vy[0]が$\frac{\sqrt{2}}{10}$ でついに無限半径の楕円軌道、つまり放物線に至ります。
そこからが少し奇妙です。軌道長半径がマイナスとなってしまいました。マイナスの半径、というのはあり得るのでしょうか。そして実際の運動は双曲線となっているのですが、これらの物理的関係を見出すことはできるのでしょうか。
周期
このあたりを深堀りするために、円軌道のもう1つの要素である周期を考えてみたいと思います。
ケプラーの法則より、惑星の公転周期$P$は、
\frac{a^3}{P^2} = \frac{G(M+m)}{4\pi^2}
となりますが、今回は都合の良い物理定数を採用しているので、
P = 2\pi{\sqrt{(\frac{r}{2-rv^2})}}^3
こんな感じになります。
vy[0] = 0.1``size=62831の時、
vy[0] = 0.12``size=15109の時、
という感じに、周期を含めて正確にシミュレートできていることがわかります。
虚数
ここでやっとメインテーマである虚数に移ります。$v$がある値を超えると、軌道長半径$a$がマイナスになりました。
ということは、計算上は、その平方根に比例する周期は虚数の周期となります。観測上では双曲線運動となっていますが。
虚数を用いれば、$v$がある値を超えると運動の種類が変わるという「場合分け」は必要なく、「惑星は$v$の値に関わらず円運動をし、その周期は軌道長半径の3乗の平方根に比例する」という1つの記述で対応できることになります。
前回の漸化式の例では「基本的には指数関数で、ある場合に振動が現れるが、それは虚数を含めて考えたら指数関数の一種である」という整理ができましたが、今回は「基本的には円軌道で、ある場合に双曲線が現れるが、それは虚数を含めて考えたら円運動の一種である」という整理ができました。また、その「境目」には、直線が現れたり、放物線が現れたりします。
もちろんこれは同じ構造を持っていて、虚数の指数が振動的な挙動を示す、またその逆も然りということは、オイラーの公式から自然に推論できます。
余談
軌跡を計算する際に、角運動量 $\vec{L}=\vec{r} \times \vec{v}$ を計算すると、角運動量保存則が(楕円や放物線においても)成り立っていることがわかります。
rvec = np.array([x[i],y[i],0])
vvec = np.array([vx[i],vy[i],0])
momentum = np.cross(rvec,vvec)
print(momentum)
以下は、vy[0]=0.1414 の時。
[ 0. 0. 14.14]
[ 0. -0. 14.14001414]
[ 0. -0. 14.14002828]
[ 0. -0. 14.14004242]
[ 0. -0. 14.14005656]
[ 0. -0. 14.1400707]
[ 0. -0. 14.14008484]
[ 0. -0. 14.14009898]
[ 0. -0. 14.14011312]
[ 0. -0. 14.14012726]...