虚数って何?
という問いに対して、的確な答えを用意するのは難しいです。信号や電気を扱う人だったらあって当たり前のものでしょうし、逆に数学に馴染みのない人には意味のない計算手段にしか感じられないと思います。
そこで、Pythonを用いて、実数のみを用いた簡単な関係式をシミュレートすると不思議な結果が出てくること、虚数を使うとそれがうまく説明できるようなケースを紹介することで、より皆様に虚数に親しみを持ってもらおうと思います。
三項間漸化式
この事例については、「虚数って何?意味あんの?」と高校生に言われたらどう答えるかという非常にわかりやすい記事が既に存在しているため、問題の数値等を一部流用させてもらっています。しかし、後半からは、記事では説明されていなかった発展的な部分について私なりの補足を書きます。
さて、三項間漸化式とは、受験数学とかではおなじみの、
\displaylines{
a_{n+2} = 5a_{n+1} - 6a_{n} \\
a_0 = 1, a_0 = 5}
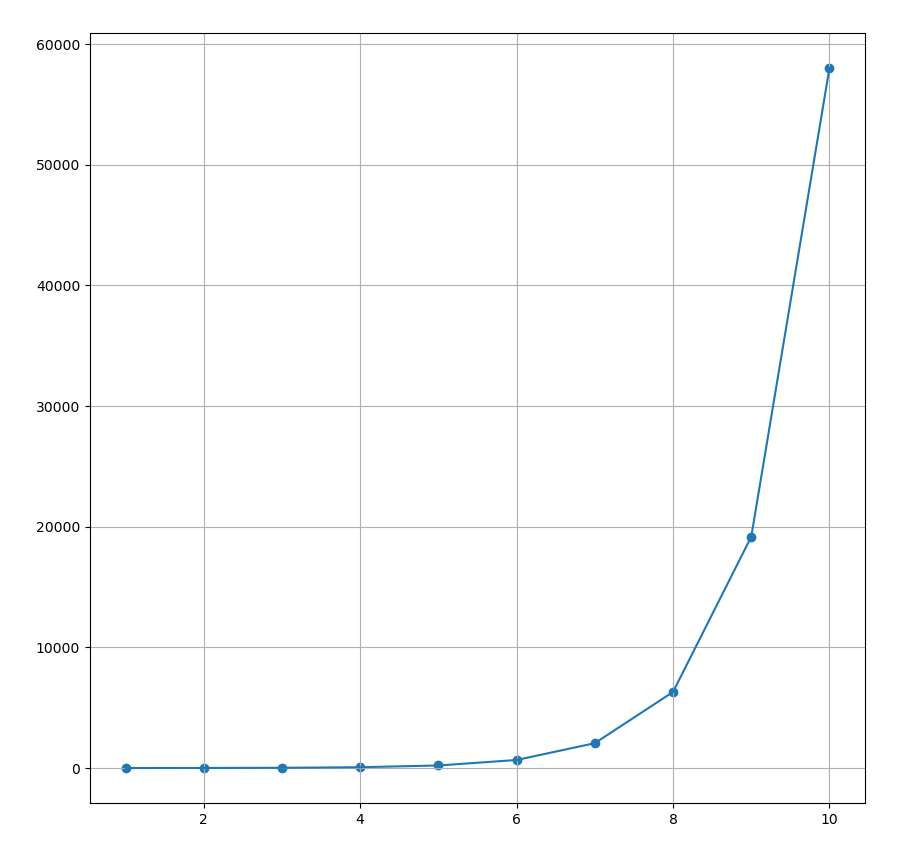
みたいなやつです。これを解くと、$1,5,19,65...$という数列が生成されて、グラフは以下のようになります。Pythonだと以下の感じでシミュレートできます。(import等は省略)
def func():
size = 10
x = np.arange(size)
y = np.zeros(size)
y[0] = 1
y[1] = 5
for i in range(size-2):
y[i+2] = 5*y[i+1] - 6*y[i]
x = x + 1
return x, y
x, y = func()
plt.figure(figsize=(10,10))
plt.scatter(x,y)
plt.plot(x,y)
plt.grid()
plt.show()
見事なまでに指数関数です。一般式は、
a_n = 3^n - 2^n
になります。
漸化式から、大体の場合は指数関数になってすごい増加をすることは予想できますが、数値の調整によっては面白い挙動をします。
a_{n+2} = 1.99a_{n+1} - a_n
これだとどうでしょう。シミュレートしてみます。
def func():
size = 100
x = np.arange(size)
y = np.zeros(size)
y[0] = 1
y[1] = 1.99
for i in range(size-2):
y[i+2] = 1.99*y[i+1] - y[i]
x = x + 1
return x, y
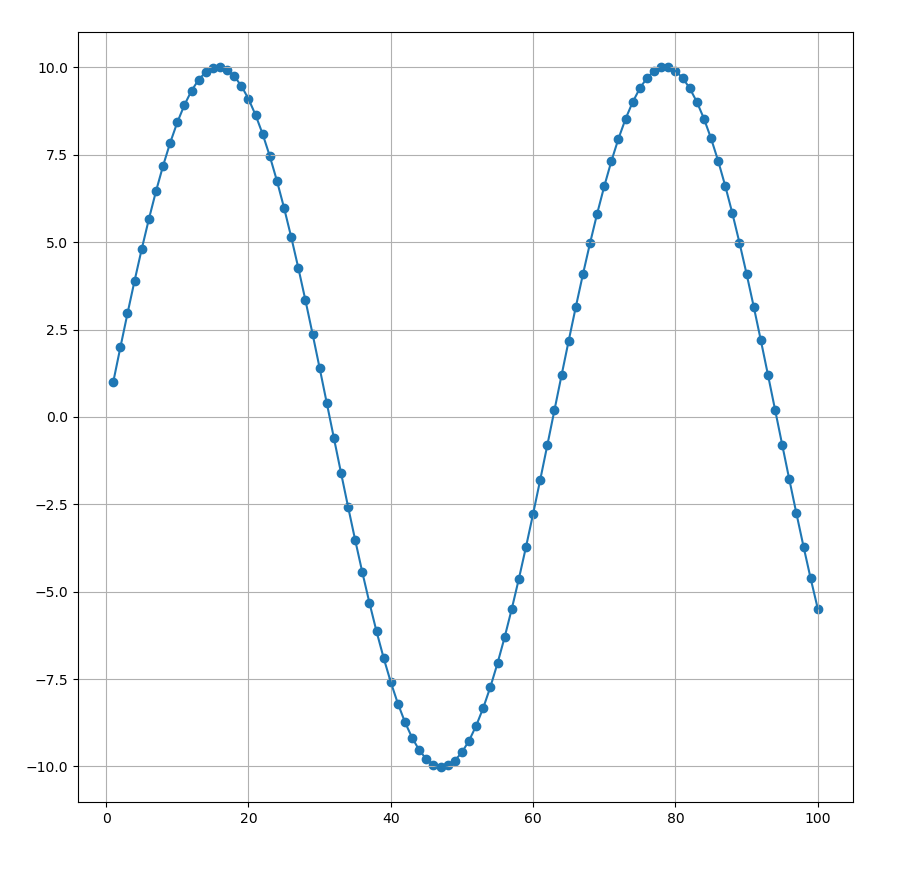
サインカーブになっている!
実際に数列を確認してみると、
[ 1. 1.99 2.9601 3.900599 4.80209201
5.6555641 6.45248055 7.18487219 7.84541511 8.42750388
8.92531762 9.33387817 9.64909994 9.86783072 9.98788319
10.00805682 9.92814989 9.74896146 9.47228341 9.10088253...
とグラフ通りの値が出力されていることがわかります。
一般式
ここからが発展部分。なぜサインカーブになるのか、その周期はどのように決定されるのかについて説明します。
そのためにはまず、三項間漸化式の一般解を求めます。
\displaylines{
a_{n+2} = p \cdot a_{n+1}-q \cdot a{n}\\
\begin{pmatrix}
a_{n+2} \\
a_{n+1} \\
\end{pmatrix}
=
\begin{pmatrix}
p & -q \\
1 & 0 \\
\end{pmatrix}
\begin{pmatrix}
a_{n+1} \\
a_n \\
\end{pmatrix}
\\
\begin{pmatrix}
a_{n+1} \\
a_{n} \\
\end{pmatrix}
=
\begin{pmatrix}
p & -q \\
1 & 0 \\
\end{pmatrix}^{n-1}
\begin{pmatrix}
a_2 \\
a_1 \\
\end{pmatrix}
\\
\begin{pmatrix}
a_{n+1} \\
a_{n} \\
\end{pmatrix}
=
\frac{1}{\beta-\alpha}
\begin{pmatrix}
\beta & \alpha \\
1 & 1 \\
\end{pmatrix}
\begin{pmatrix}
\beta & 0 \\
0 & \alpha \\
\end{pmatrix}^{n-1}
\begin{pmatrix}
1 & -\alpha \\
-1 & \beta \\
\end{pmatrix}
\begin{pmatrix}
a_2 \\
a_1 \\
\end{pmatrix}
\\
(\alpha,\betaは固有値)\\
(\alpha+\beta = p \alpha \cdot \beta =q)\\
\begin{pmatrix}
a_{n+1} \\
a_{n} \\
\end{pmatrix}
=
\frac{1}{\beta-\alpha}
\begin{pmatrix}
\beta & \alpha \\
1 & 1 \\
\end{pmatrix}
\begin{pmatrix}
\beta^{n-1} & 0 \\
0 & \alpha^{n-1} \\
\end{pmatrix}
\begin{pmatrix}
1 & -\alpha \\
-1 & \beta \\
\end{pmatrix}
\begin{pmatrix}
a_2 \\
a_1 \\
\end{pmatrix}}
このまま解くと少し複雑になるので、都合の良い初期値 $a_1=1,a_2=\beta+\alpha$ を選びます。
\displaylines{
a_{n}
=
\frac{1}{\beta-\alpha}
\begin{pmatrix}
1 & 1 \\
\end{pmatrix}
\begin{pmatrix}
\beta^{n-1} & 0 \\
0 & \alpha^{n-1} \\
\end{pmatrix}
\begin{pmatrix}
1 & -\alpha \\
-1 & \beta \\
\end{pmatrix}
\begin{pmatrix}
\beta + \alpha \\
1 \\
\end{pmatrix}
\\
a_{n}=
\frac{1}{\beta-\alpha}
\begin{pmatrix}
1 & 1 \\
\end{pmatrix}
\begin{pmatrix}
\beta^{n-1} & 0 \\
0 & \alpha^{n-1} \\
\end{pmatrix}
\begin{pmatrix}
\beta \\
-\alpha \\
\end{pmatrix}
\\
a_{n}=
\frac{1}{\beta-\alpha}
\begin{pmatrix}
1 & 1 \\
\end{pmatrix}
\begin{pmatrix}
\beta^n \\
-\alpha^n \\
\end{pmatrix}
\\
a_{n}=
\frac{1}{\beta-\alpha}
(\beta^n - \alpha^n)}
以上が一般式になります。冒頭に示したケースは $\beta=3,\alpha=2$ のものになります。(余談ですが、 $\beta = \frac{1+\sqrt{5}}{2},\alpha=\frac{1-\sqrt{5}}{2}$ だとフィボナッチ数列になります)
これを別の見方から言えば、先に$\alpha$と$\beta$を決めてしまえば、どのような指数関数でも生み出せるということです。また、
- $\alpha$と$\beta$の絶対値がともに $1$ 未満 $\rightarrow$ 収束
- $\alpha$と$\beta$の絶対値のいずれかが $1$ より上 $\rightarrow$ 発散
- どちらでもないとき $\rightarrow$ 振動
となることも伺えます。
虚数を入れてみる
せっかくなので、$\alpha$と$\beta$に虚数を入れてみましょう。$\alpha$と$\beta$は二次方程式の解ゆえに共役になることに注意すると、例えば$\beta=i,\alpha=-i$はどうでしょうか。
a_{n} = \frac{1}{2i}(i^n-(-i)^n)
初期値を$1,0$としてこれを計算すると $1,0,-1,0,1...$ という数列になることがわかります。実は、漸化式の形に直すと、
\displaylines{
a_{n+2} = p \cdot a_{n+1} - q \cdot a_n \\
p = i + -i = 0 \\
q = i \cdot -i = -i^2 = 1 \\
a_{n+2} = -a_{n} \\}
となります。こうして見ると単純な漸化式ですが、一般式が虚数を使った形になるのは面白いですね。
周期関数として一般化
さて、このようなバーチャル三角関数(今名付けました)をもう少し一般化できないでしょうか。$\alpha$と$\beta$の絶対値がともに1の時、$a_n$は振動する周期関数となりますが、両者が共役であることを考えると複素数平面上にある単位円1上の共役複素数であるということになります。つまり、適当な$\theta$を用いて、
\displaylines{
\beta = \cos{\theta} + i \cdot \sin{\theta} \\
\alpha = \cos{\theta} - i \cdot \sin{\theta} \\}
と一般化できます(上の例は$\theta=\frac{\pi}{2}$の時)。また、これはオイラーの公式を用いて、
\displaylines{
\beta = e^{i\theta} \\
\alpha = e^{-i\theta}
}
と更に簡潔に記述できます。
これにより、「振動する漸化式」は、1つの変数 $\theta$ を用いて
\displaylines{
a_{n+2} = (\beta + \alpha) \cdot a_{n+1} - \beta \cdot \alpha \cdot a_n \\
a_{n+2} = 2\cos{\theta} \cdot a_{n+1} - a_n\\}
一般式(※初期値 $a_1 = 1,a_2=\beta + \alpha$ )は
\displaylines{
a_{n} = \frac{1}{e^{i\theta}-e^{-i\theta}}(e^{in\theta} - e^{-in\theta}) \\
a_{n} = \frac{1}{2i \cdot \sin{\theta}} 2i \sin{n\theta} \\
a_{n} = \frac{1}{\sin{\theta}}\sin{n\theta}}
と表現することができます。
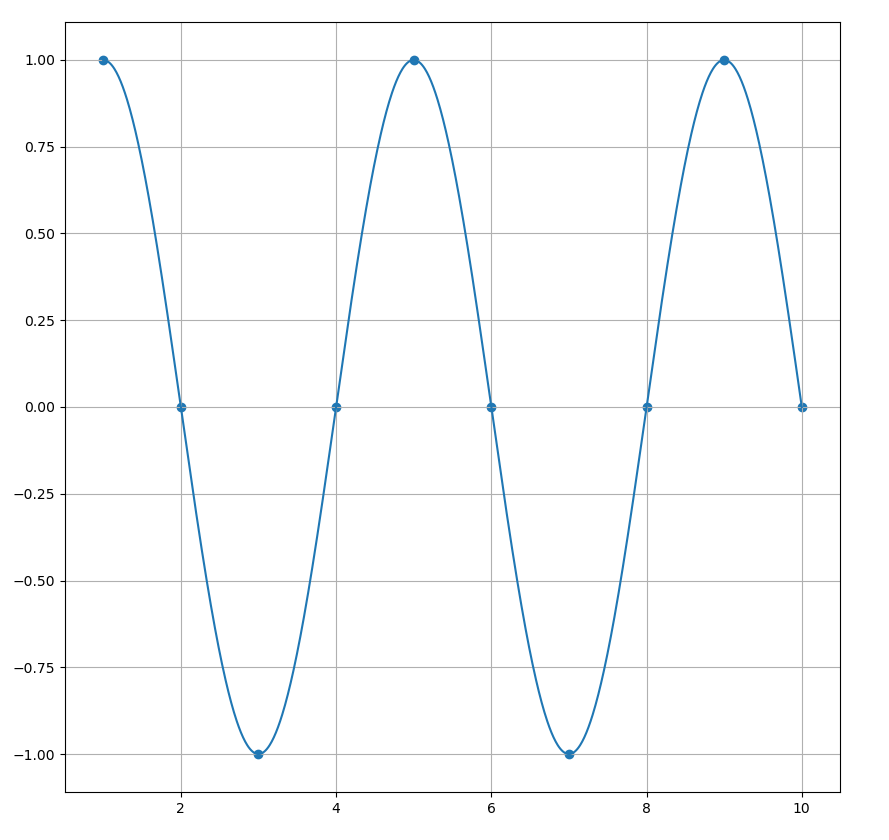
実際に、先程の例で検証してみましょう。$\beta=i,\alpha=-i$ の時、$\theta = \frac{\pi}{2}$ となるので、
\displaylines{
a_n = \frac{1}{\sin{\frac{\pi}{2}}} \cdot \sin{\frac{\pi}{2}n} \\
a_n = \sin{\frac{\pi}{2}n}}
実際に計算すると、$1,0,-1,0,1...$ という数列になることがわかります。
def disc():
size = 10
x = np.arange(size)
y = np.zeros(size)
y[0] = 1
y[1] = 0
for i in range(size-2):
y[i+2] = - y[i]
x = x + 1
return x, y
def cont():
x = np.linspace(1,10,1000)
y = np.sin(x*np.pi/2)
return x, y
p,q = cont()
x,y = disc()
plt.figure(figsize=(10,10))
plt.plot(p,q)
plt.scatter(x,y)
plt.plot(x,y)
plt.grid()
plt.show()
漸化式としては単純ですが、背後にはこのような三角関数が潜んでいると考えることもできます。
振幅も周期も係数によって決まる
ここで、少し前に出した
a_{n+2} = 1.99a_{n+1} - a_n
について考えてみます。
こちらはかなりダイナミックなサインカーブになっています。このような振幅と周期はどのように決まるのでしょうか。
もともと $\theta$ は $\beta+\alpha=2\cos{\theta}$ という計算に使う値でした。ということは、
\theta = \cos^{-1}(\frac{\beta + \alpha}{2})
という逆計算によって、振幅と周期が同時に決まるということになります。
検証してみます。振幅$A$と周期$T$は
\displaylines{
\cos^{-1}{\frac{1.99}{2}} \simeq 0.100 \\
A \simeq 0.100^{-1} = 10.0 \\
T \simeq 2\pi \cdot 0.100^{-1} = 62.8}
と計算されますが、上のグラフがよく一致していることがわかります。この値は $a_{n+1}$ が2に近づくほど指数関数的に伸びて周期と上限は無限大に近づきます。2になると重解となって直線となります。2を超えると指数関数になります。
三間項漸化式を、虚数を含めた指数関数の一種と捉えると、係数によって色々な曲線が生成されることの、その全体像を掴みやすくなります。
間接的な結果しか観測できないのでは?
それでも、上のように思う人もいると思います。グラフがサインカーブになることはわかった。でもそれは間接的な観測でしかないのではないかと。
しかし、観測を通してしかその存在を確認をできないというのは、実数も同じではないでしょうか。
$1$ 箱みかん $300$ 個入の段ボールが $100$ 個あるのでみかんが $30,000$ 個ある、という計算をする時、誰も $30,000$ 個のみかんをその目で確認している訳ではありません。誰かが頑張って $30,000$ 個人力で数える? 確認中、目を離した場所にあるみかんは本当に存在しているのですか? ...という懐疑論を出すまでなく、そのような作業をミスなく一貫性を持って行うのはほぼ不可能です。しかし、日常的には $300 \times 100=30,000$ という「計算」で済ませてしまって問題ありません。
そういった意味では、我々は数の上では、計算のつじつまが合うだけのイリュージョンの生活を送っているのです。それが破綻しなく便利だから計算というマジックを採用しているだけの話です。(多く現代人なら日常的に行う複利計算も、金融に疎い人から見たら得体のしれないインチキに見えるかもしれません)
そして、それは虚数も同じです。別に虚数が(物理的に?)存在しようとしまいとと計算のつじつまが合って便利だから、場合分けの手間が省けるから使うだけです。その点は、実数を使う理由と何ら変わることはありません。
続編
もうひとつのケースとして、惑星の公転軌道について話そうと思っていたのですが、疲れたので、またすごい文量になってきたので一旦休みます。10いいねぐらいついたら続編を書きます(乞食)。
(追記:続編の惑星の軌道編を書きました)