想定読者
- ABC359-C で苦しんだ人
- 公式解説とは違う角度での解説が欲しい人
- 座標系とか座標変換とかに興味がある人
- その他数学全般が好きな人
ヘックス座標系での最短距離
ABC359-C は、要約するとヘックス座標系(六角形のマス目からなる座標系)の最短距離を求める問題でした。公式解説では、以下の数式により高速に求められると述べられています。
\text{dist} = \frac{|y|+\text{max}(|x|,|y|)}{2}
ここで、ヘックス座標系での最短距離を、違う観点から考えてみます。
とりあえず問題の設定は忘れて、ヘックス座標での最短距離を並べてみましょう。
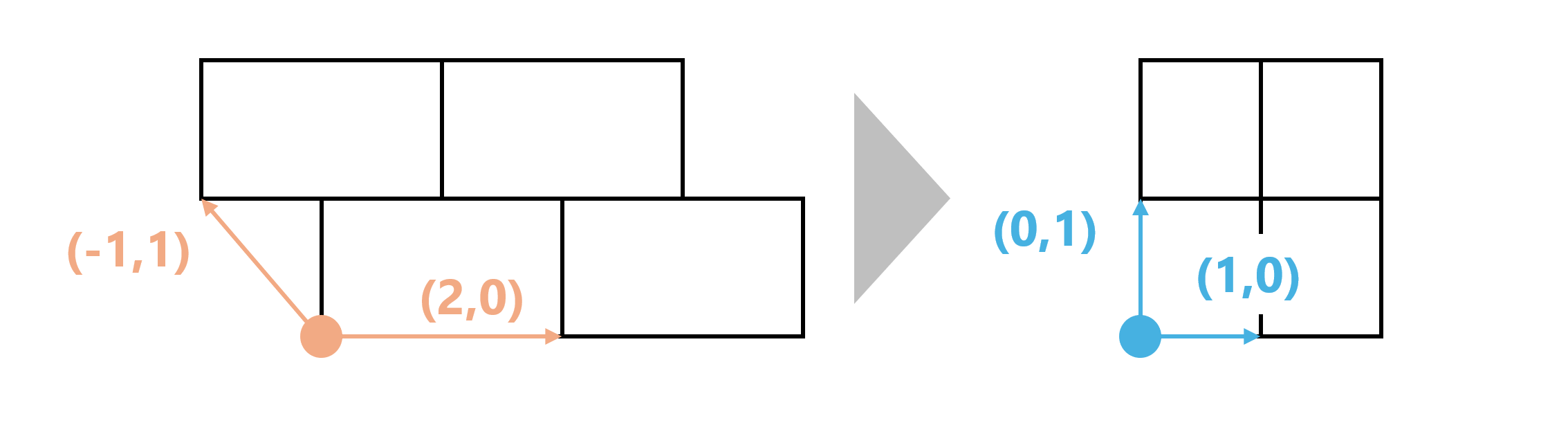
これを 無理矢理 直交座標系に変換することを考えます。互い違いに 1/2 マスずつずれているので、それを右にせん断するようにずらすと以下のようになります。

この時、原点 $(0,0)$ から見て右上と左下の領域は正方形、左上と右下の領域は直角三角形の形になります。また、正方形の領域の最短距離はいわゆるチェビシェフ距離、直角三角形の領域はいわゆるマンハッタン距離になります。
つまり、変換後の座標を $x',y'$ とすると、答えは以下です。
- 正方形の領域にあるとき $\text{max}(|x'|,|y'|)$
- 直角三角形の領域にあるとき $|x'|+|y'|$
問題に戻ります。直交座標系で与えられていた横長のタイルを、上のような形に矯正するためにはどうすればいいか。
$e_x=(2,0),e_y=(-1,1)$ から、$e'_x=(1,0),e'_y=(0,1)$ への基底変換を行えばよいので、
\displaylines{
\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 & -1 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} x' \\ y' \end{pmatrix} \\
\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} 2 & -1 \\ 0 & 1 \end{pmatrix}^{-1}\begin{pmatrix} x \\ y \end{pmatrix} \\
\begin{pmatrix} x' \\ y' \end{pmatrix} = \frac{1}{2}\begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix}^{-1}\begin{pmatrix} x \\ y \end{pmatrix}
}
$x',y'$ が第 $1,3$ 象限にある時はチェビシェフ距離、第 $2,4$ 象限にある時はマンハッタン距離となるので、
- $x'y'\geq 0$ のとき $\text{max}(|x'|,|y'|)$
- $x'y'< 0$ のとき $|x'|+|y'|$
元の座標系に直すと、以下が答えになります。
- $(x+y)\cdot y\geq 0$ のとき $\text{max}(\frac{|x+y|}{2},|y|)$
- $(x+y)\cdot y< 0$ のとき $\frac{|x+y|}{2}+|y|$
(なお、本番中は、こんな本質は見えずに、気合の場合分けと二分探索でなんとかしました)
ヘックス座標系と距離空間
面白いのはここからで、以下の事実が示唆されます。
- ヘックス座標系における距離は、チェビシェフ距離とマンハッタン距離の両方の性質を併せ持つ
- ヘックス座標系での六角形は、直交座標系において正方形と直角三角形を組み合わせた領域と一対一対応を持つ
ヘックス座標系における距離をヘックス距離と定義します。
距離を定義すると、円 が定義できます。まるいやつ(だけ)ではなく、ある点から等距離にある集合と定義します。
- マンハッタン距離の 円 は、ひし形となる
- チェビシェフ距離の 円 は、正方形となる
- ユークリッド距離の 円 は、円となる
ヘックス距離の 円 は、正方形とひし形を半分ずつ合成したものになります。これは六角形と考えることもできます。これをせん断変形したものは、正六角形を並べた座標として理解しやすいため、戦略シミュレーションゲームなどでは良く採用されます。
チェスの駒が生み出す距離空間
更に、このことを別の面から考えて「どのような移動手段がどのような距離を生み出すか」を考えます。
マンハッタン距離は、タテ・ヨコを $1$ マスずつ移動することから定義することもできます。
チェスにはそのようなコマは存在しませんが、仮想的に、以下のようなコマが存在した場合、マンハッタン距離とは、以下のコマが移動する時の最短経路になります。
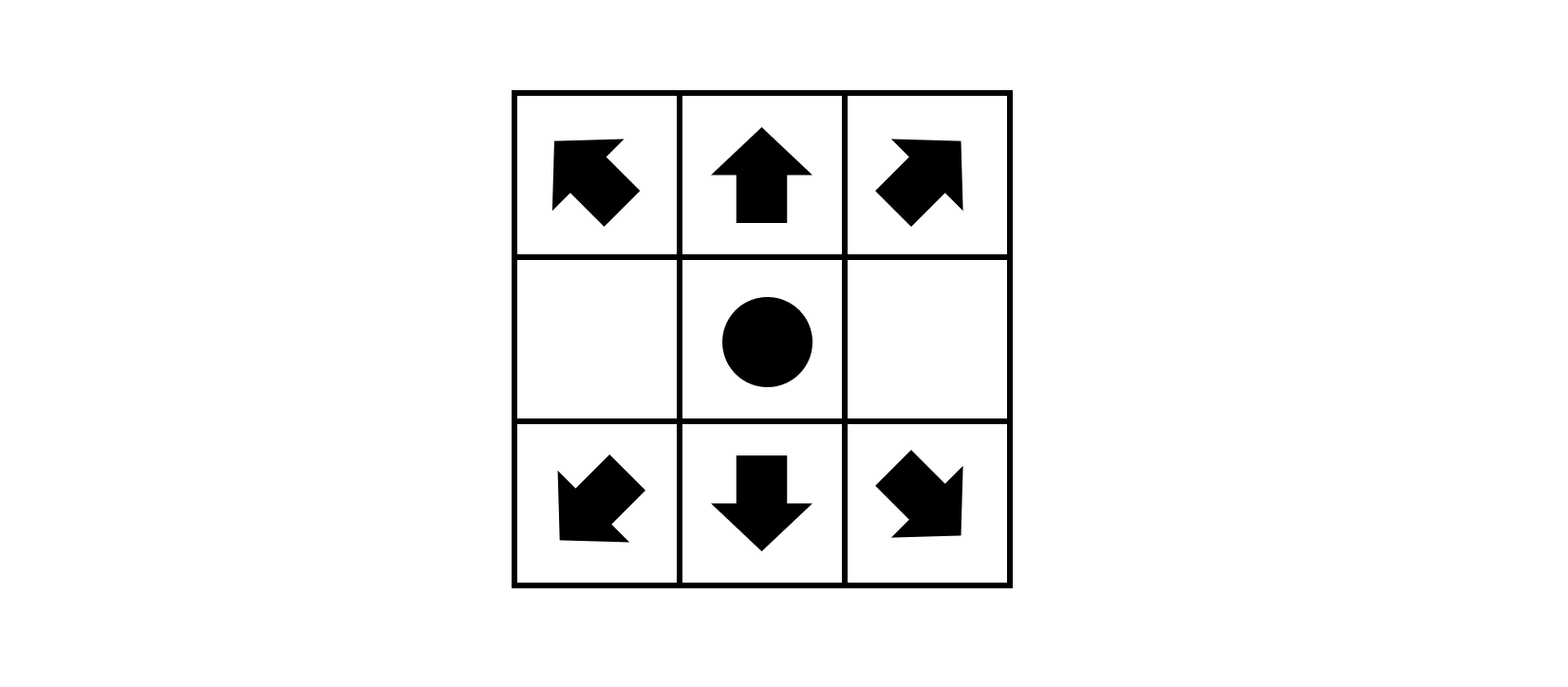
では、チェビシェフ距離は? これは実は キングの最短経路 がまさにそれになります。
そして、ヘックス距離を生み出すようなコマは当然、以下のような移動手段を持つと考えられます。
もしそのようなコマが存在した場合、直交座標系の中でこのコマだけは六角座標系を生きていると言えなくもないです。
他にも、「座標系」を生み出すようなコマは存在するでしょうか?
ポーン
- - - - - 5 - - - - -
- - - - - 4 - - - - -
- - - - - 3 - - - - -
- - - - - 2 - - - - -
- - - - - 1 - - - - -
- - - - - 0 - - - - -
- - - - - - - - - - -
- - - - - - - - - - -
- - - - - - - - - - -
- - - - - - - - - - -
- - - - - - - - - - -
ポーンの移動は距離の公理を満たしません。逆移動不可能な点があるため、任意の点同士における $d(x,y)=d(y,x)$ を満たさないからです。
ルーク
2 2 2 2 2 1 2 2 2 2 2
2 2 2 2 2 1 2 2 2 2 2
2 2 2 2 2 1 2 2 2 2 2
2 2 2 2 2 1 2 2 2 2 2
2 2 2 2 2 1 2 2 2 2 2
1 1 1 1 1 0 1 1 1 1 1
2 2 2 2 2 1 2 2 2 2 2
2 2 2 2 2 1 2 2 2 2 2
2 2 2 2 2 1 2 2 2 2 2
2 2 2 2 2 1 2 2 2 2 2
2 2 2 2 2 1 2 2 2 2 2
ルークの移動は距離の公理を満たします。
- $x=0$ かつ $y=0$ のとき $0$
- それ以外で $x=0$ または $y=0$ のとき $1$
- それ以外のとき $2$
ビショップ
1 - 2 - 2 - 2 - 2 - 1
- 1 - 2 - 2 - 2 - 1 -
2 - 1 - 2 - 2 - 1 - 2
- 2 - 1 - 2 - 1 - 2 -
2 - 2 - 1 - 1 - 2 - 2
- 2 - 2 - 0 - 2 - 2 -
2 - 2 - 1 - 1 - 2 - 2
- 2 - 1 - 2 - 1 - 2 -
2 - 1 - 2 - 2 - 1 - 2
- 1 - 2 - 2 - 2 - 1 -
1 - 2 - 2 - 2 - 2 - 1
ビショップの移動は距離の公理を満たします。ただし、要素は $x+y$ が偶数となるような $(x,y)$ に限られます。$d(x,y)$ の定義は以下。
- $x=0$ かつ $y=0$ のとき $0$
- それ以外で $x=y$ または $x=-y$ のとき $1$
- それ以外のとき $2$
以上のことから、ビショップは、盤面の約半分は絶対に移動できないことがわかります。
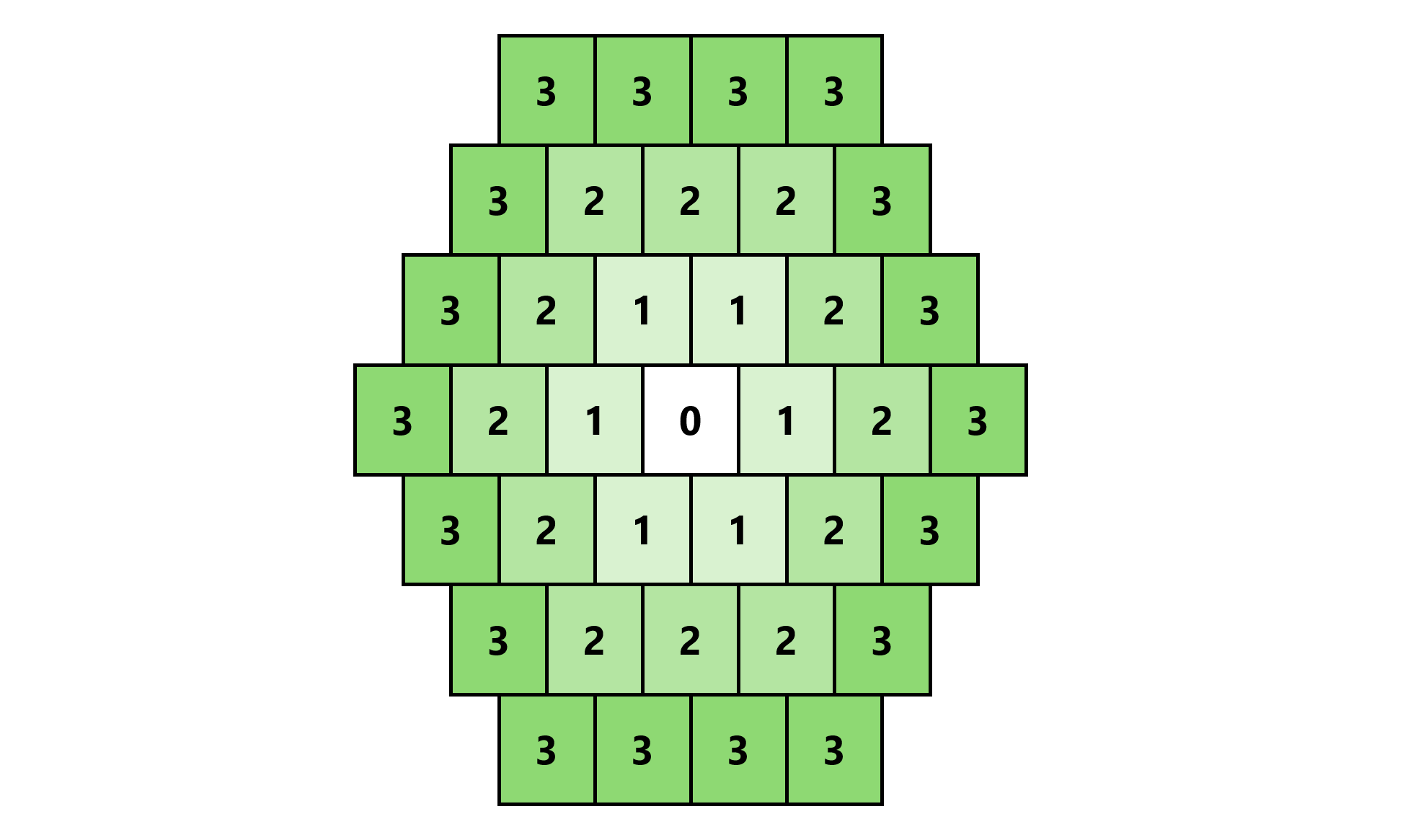
クイーン
1 2 2 2 2 1 2 2 2 2 1
2 1 2 2 2 1 2 2 2 1 2
2 2 1 2 2 1 2 2 1 2 2
2 2 2 1 2 1 2 1 2 2 2
2 2 2 2 1 1 1 2 2 2 2
1 1 1 1 1 0 1 1 1 1 1
2 2 2 2 1 1 1 2 2 2 2
2 2 2 1 2 1 2 1 2 2 2
2 2 1 2 2 1 2 2 1 2 2
2 1 2 2 2 1 2 2 2 1 2
1 2 2 2 2 1 2 2 2 2 1
クイーンの移動は距離の公理を満たします。$d(x,y)$ の定義は省略します。
ハーフキング
キング……はもう論じたので、以下のような動きをする、ハーフキング を考えます。
5 5 5 5 5 5 5 5 5 5 5
6 4 4 4 4 4 4 4 4 4 6
5 5 3 3 3 3 3 3 3 5 5
6 4 4 2 2 2 2 2 4 4 6
5 5 3 3 1 1 1 3 3 5 5
6 4 4 2 2 0 2 2 4 4 6
5 5 3 3 1 1 1 3 3 5 5
6 4 4 2 2 2 2 2 4 4 6
5 5 3 3 3 3 3 3 3 5 5
6 4 4 4 4 4 4 4 4 4 6
5 5 5 5 5 5 5 5 5 5 5
これも「距離」になりますが、ヘックス移動に比べて少し複雑です。円を直感的に描くことも難しいです。$d(x,y)$ の定義は以下。
- $y^2\geq x^2$ のとき $|y|$
- $y^2< x^2$ かつ $x+y$ が偶数のとき $|x|$
- $y^2< x^2$ かつ $x+y$ が奇数のとき $|x|+1$
ハーフナイト
ナイトが実質的なラスボスなので、その前に簡単な ハーフナイト について触れます。
これがハーフナイトです。
- - - 7 - - 4 - - 3 -
- 8 - - 5 - - 2 - - 3
- - 6 - - 3 - - 2 - -
7 - - 4 - - 1 - - 2 -
- 5 - - 2 - - 1 - - 4
- - 3 - - 0 - - 3 - -
4 - - 1 - - 2 - - 5 -
- 2 - - 1 - - 4 - - 7
- - 2 - - 3 - - 6 - -
3 - - 2 - - 5 - - 8 -
- 3 - - 4 - - 7 - - -
これは基底 $e_x=(2,1),e_y=(1,2)$ を用いた実質的な直交座標系とみなすことができます。当然、距離の公理を満たします。
ナイト
ラスボスのナイトです。こいつが一番、変な動きをします。
4 3 4 3 4 3 4 3 4 3 4
3 4 3 2 3 2 3 2 3 4 3
4 3 2 3 2 3 2 3 2 3 4
3 2 3 4 1 2 1 4 3 2 3
4 3 2 1 2 3 2 1 2 3 4
3 2 3 2 3 0 3 2 3 2 3
4 3 2 1 2 3 2 1 2 3 4
3 2 3 4 1 2 1 4 3 2 3
4 3 2 3 2 3 2 3 2 3 4
3 4 3 2 3 2 3 2 3 4 3
4 3 4 3 4 3 4 3 4 3 4
ナイトの世界で生きると、隣に見えるコマよりもその遠くの方が「近い」変な世界になります。$d(x,y)$ の定義はできるでしょうか?
これが思ったより超複雑で難儀していたのですが、何事にも先達はいるもので先行研究がみつかりました。
結論として、以下が $d(x,y)$ の定義になります。
- $(x,y)=(0,0)$ のとき $0$
- $(x,y)=(1,0),(0,1),(-1,0),(0,-1)$ のとき $3$
- $(x,y)=(2,2),(-2,2),(-2,-2),(2,-2)$ のとき $4$
- それ以外のとき
- $a=\text{max}(\frac{|x|}{2},\frac{|y|}{2},\frac{|x|+|y|}{3})$ を四捨五入したものとする
- $2$ で割ったあまりを $\text{mod}2$ と定義する
- $d(x,y)=a+(a+|x|+|y|)\text{mod}2$