やったこと
ストラテジーゲームとかで採用されるヘクスマップ(六角形を敷き詰めたやつ)における「距離」を考えてみました。
ヘクスマップにおける「円」
簡単のために、まず原点中心半径1の円を書くことを考えます。
ヘクスマップにおける「円」は正六角形になります。
ここで、チェビシェフ距離やマンハッタン距離では「円」が正方形になることを利用します。
下図は適当にGrapherで書いた、チェビシェフ距離とマンハッタン距離での半径1の円。斜めになってる方がマンハッタン。
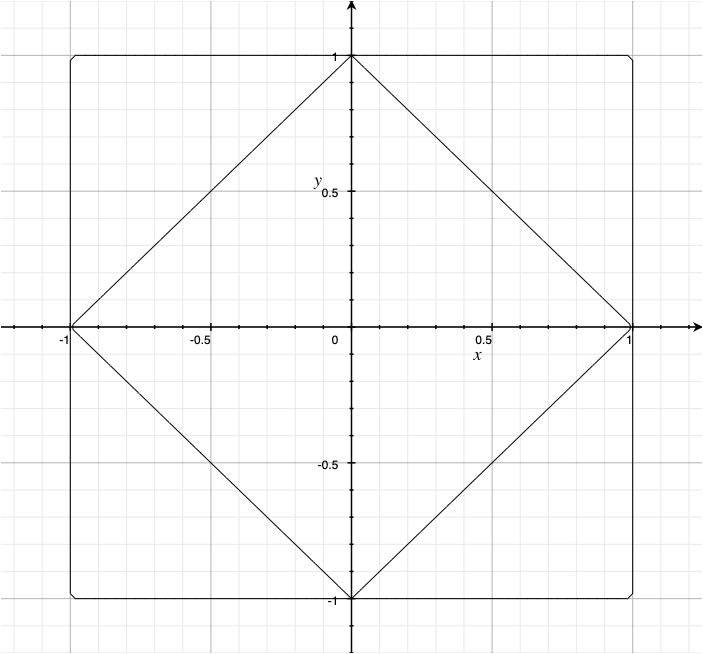
というわけでこれを活用して、$120^{\circ}$で交わる斜交座標系で、以下のように第一・第三象限ではチェビシェフ距離、第二・第四象限ではマンハッタン距離を取るようにすれば良い。

式にするとこんな感じ。
1 =
\begin{cases}
\max(|\ x'|,|\ y'|) & (x'y' \geq 0) \\
|\ x'|+|\ y'| & (x'y' < 0)
\end{cases}
斜交座標だと使いにくいので、直交座標との変換式も載せておく。(「'」が付いてないのが直交座標、付いてるのが120度斜交座標)
\begin{align}
x' &= x+\frac{y}{\sqrt{3}} \\
y' &= \frac{2y}{\sqrt{3}}
\end{align}
これをgrapherに突っ込んでみると...

いい感じに正六角形の円が描けた。
へクスマップにおける距離
ここまではあくまで原点からの距離を考えていたので、最後に二点間の距離に一般化するとこんな感じ。(120度斜交座標)
d((x'_1,y'_1),(x'_2,y'_2)) =
\begin{cases}
\max(|\ x'_1 - x'_2|,|\ y'_1 - y'_2|) & ((x'_1-x'_2)(y'_1-y'_2) \geq 0) \\
|\ x'_1 - x'_2|+|\ y'_1 - y'_2| & ((x'_1-x'_2)(y'_1-y'_2) < 0)
\end{cases}
ちなみに、
\begin{align}
d(x,y) &\geq 0 \\
d(x,y) &= 0\ \textrm{if and only if}\ (x=y) \\
d(x,y) &= d(y,x) \\
d(x,z) &\leq d(x,y) + d(y,z)
\end{align}
という距離関数の定義を満たす気がするので、厳密性ガチ勢の方でもたぶん安心です。
で?
特にこれといった応用は思いついていません。
ボロノイ図を使ったゲームみたいなものを作っている最中に、マンハッタン距離ともユークリッド距離とも違う面白い距離関数はないかと、気まぐれにこの距離を考えてみたのですが、そのゲームについてはまたの機会に。
ちなみに、マンハッタン距離、チェビシェフ距離、ユークリッド距離、今回作った距離(Hex距離とでも言いましょうか)における、原点中心半径1の円を並べて描くとこんな感じ。

Hex距離はマンハッタン距離とユークリッド距離の間くらいの性質を持っていそうなので、この性質を使った応用が何かあるかもしれません。
何かいいアイデアがあったら教えてください。