遅延セグメントツリーのモノイドを†理解†して自作できるようになろう

　皆さんも、そろそろ遅延セグメントツリー（遅延セグ木）を †カスタマイズ† する領域に到達しつつあるのではないでしょうか。

　チートシートに頼らずとも、自力でモノイドを構築できるようにしましょう。

以後、ACL（AtCoder Library）の lazy_segtree を基準に話しますが、本質は他のライブラリでも変わりません。

通常のセグ木の op と e は理解している前提で話します。理解していない場合、この先を読み進めるのはつらいと思います。

　ACL では、遅延セグ木のコンストラクタは以下のように定義されます。

• lazy_segtree<S, op, e, F, mapping, composition, id> seg(int n);

　これらの各要素を丁寧に解説していきます。

S

　まず、　S は Segment のことです。確証はないですがほぼ間違いないと思います。

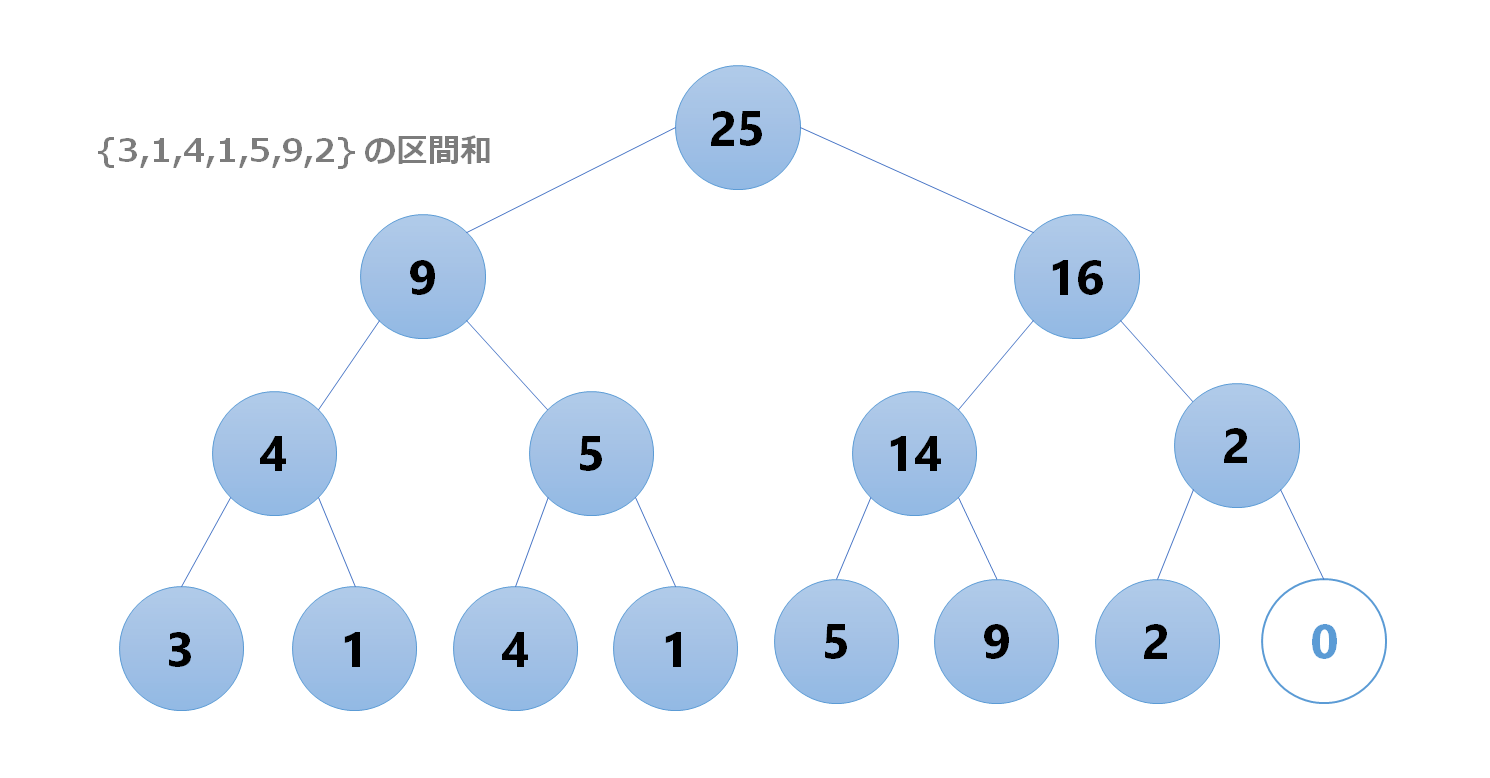
　下の図は、通常のセグ木においてセグメントを構築するときの図です。

　このノードのひとつひとつがセグメントです。通常のセグ木を理解していればこれは大丈夫だと思います。

op

　op はセグメント同士を結合するときのはたらきです。おそらく Operation でしょうか。ライブラリによっては、merge と称されることもありますが、こちらの方がはたらきを想像しやすいです。

　要は、ふたつのセグメントを結合するときに、どのようなセグメントを残すかです。

e

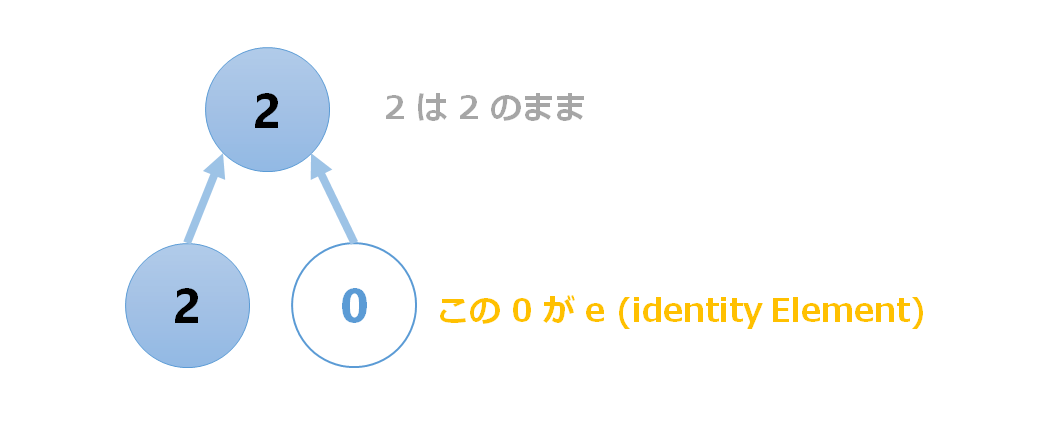
　e は単位元です。単位元のことを英語で identity Elementと言いますが、その E だと思います（たぶん）。

　これは、作用させても何も影響を与えないようなものを指します。

• + ならば $0$
• XOR ならば $0$
• * ならば $1$
• max ならば、事実上無限小とみなせる十分小さい値
• min ならば、事実上無限大とみなせる十分大きな値

　等です。

F

　このあたりから、遅延セグ木独特の要素が入ってきます。F は Function の略です（だと思います）。日本語にすると関数ですが、ここでははたらきを想像しやすくするために 作用素 と呼ぶことにします。

　これは、セグメントに対してある「作用」をする要素です。

• 区間加算ならば、加算する値
• 区間変更ならば、変更先となる値

　等です。

　遅延セグ木の apply とは、指定した範囲のセグメントにある F を作用させることを指します。

　図にするとこんな感じです。

　S がカスタマイズによっては複雑になっていく一方で、F は単純なかたちを保つ傾向があります（なんとなく）。なので、ほとんどの場合は、独自に構造体を定義するまでもなく、int とか long long とかを直接利用しても大丈夫だと思います。

mapping

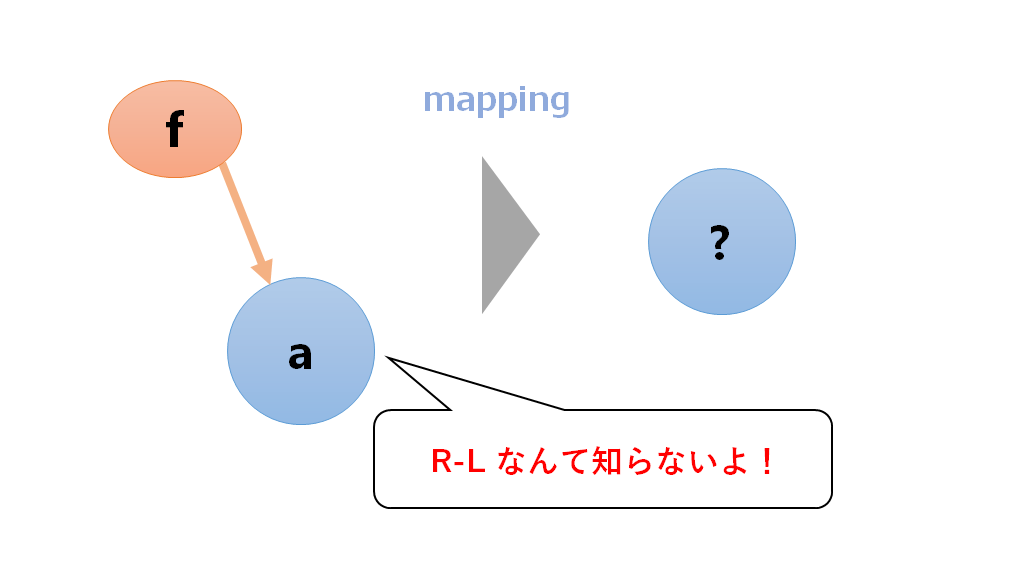
　日本語にすると写像です。作用素がセグメントにどう作用するかを決めます。

　大事なこととして、mapping の型はセグメント になります。図にすると以下のような感じになります。

composition

　日本語にすると合成です。

　作用素同士がぶつかったとき（apply が重ねがけされたとき）にどうするかを決めています。大事なこととして、composition の型は作用素 になります。つまり F です。

　ここが理解できれば遅延セグ木のモノイドの本質を理解できたといってよいと思います。

　図にすると以下のようになります。

　また、composition には順序があります。composition(F f,F g) は数学の関数のかたちで表すと $f \circ g$ となり、要は $g$ を作用させた 後 に $f$ を作用させます。この順序は区間変更などでは重要です。

id

　作用素の 単位元です。（これに対して、e はセグメントの単位元です）

　IDentity element の ID だと思います。余談ですが、この名前は、言語によっては予約語とぶつかる（少なくとも Python では）ので、すこし困るところです。

　これは、セグメントに作用させても、何もそのセグメントを変化させないような作用素になります。

練習：区間加算区間最小値

　では、実際に構築していきます。区間最小値なので、

int op(int a,int b){
    return min(a,b);
}
int e(){
    return INT_MAX;
}

　は既知です。

　区間加算はどうなるでしょうか？

　ある区間に一定の値を足せば、そのどこかは最小値になるので、当然最小値もその分足されます。よって、

int mapping(int f,int a){
    return f+a;
}

　となります。また、加算同士の合成は当然に加算であり、その単位元は $0$ なので、他の設定も以下のようになります。

int composition(int f,int g){
    return f+g;
}
int id(){
    return 0;
}

　これで設定が完了しました。なお、

• セグメントには a, b
• 作用素には f, g

　という変数名を充てています。

　なお、mapping を考えるにあたっては、数式で考えることもできます。

\displaylines{
\min_{i \in [l,r)} (a_i + f) = \min_{i \in [l,r)} a_i + \min_{i \in [l,r)} f \\
= \min_{i \in [l,r)}a_i + f \\

}

　

練習：区間変更区間最小値

　区間最小値なので以下は既知。

int op(int a,int b){
    return min(a,b);
}
int e(){
    return INT_MAX;
}

　作用素がすこし厄介で、

• 作用素があるならそれに
• ないならそのまま

　というかたちになります。このとき、単位元に $0$ を指定するようなことをすると、

• それとも単位元なのか？
• これは $0$ に改変したいのか？

　ということが曖昧になるのでよくないです。実用上は、「ありえない値」（事実上無限大や事実上無限小）を事実上の単位元に充てることが多いです。

　すべての値を改変するので、最小値は当然それになります。

int ID = 2e9; // 制約上ありえない値など
int mapping(int f,int a){
   if(f != ID){
       return f;
   }
   return a;
}

　合成については、介入する関数（f）が単位元なら何もせず、そうでないならその値にします。

int composition(int f,int g){
   if(f != ID){
       return f;
   }
   return g;
}

　数式では以下のような感じに。

\displaylines{
\min_{i \in [l,r)} a_i = \min_{i \in [l,r)}f
= f （f が単位元でないとき）
}

練習：区間加算区間和

　このあたりからすこし難しくなります。その理由を説明するために、まず区間和の数式を出します。

\displaylines{
\sum_{i \in [l,r)} (a_i + f) = \sum_{i \in [l,r)}  a_i + \sum_{i \in [l,r)} f \\
= \sum_{i \in [l,r)}  a_i + (r-l) \cdot f
}

　ここで困ったことが起こります。

　セグメントが持っているのは「今までの合計」だけです。なので、この mapping を成立させるためには、$r-l$、つまり自分のセグメントが分担している範囲も知っている必要があります。

　そのために、「長さ」の情報を追加した、以下のようなセグメントツリーを考えます。

　こうすれば、セグメントに対する作用素を計算できます。

　以上の内容を踏まえて、コードにします。

struct S
{
    int size;
    int sum;
};
S op(S a,S b){
    return {a.size+b.size,a.sum+b.sum};
}
S e(){
    return {0,0};
}
S mapping(int f,S a){
    return {a.size,a.sum+f*a.size};
}
int composition(int f,int g){
    return f+g;
}
int id(){
    return 0;
}

練習：区間乗算区間和

\displaylines{
\sum_{i \in [l,r)} (f \cdot a_i) = f\sum_{i \in [l,r)}  a_i \\
}

　シンプルですね。

int op(int a,int b){
    return a+b;
}
int e(){
    return 0;
}
int mapping(int f,int a){
    return f*a;
}
int composition(int f,int g){
    return f*g;
}
int id(){
    return 1;
}

参考：区間加算区間二乗和

\displaylines{
\sum_{i \in [l,r)} (a_i + f)^2 = \sum_{i \in [l,r)} (a_i^2+2a_i \cdot f + f^2)\\
= \sum_{i \in [l,r)}  a_i^2 + \sum_{i \in [l,r)}2a_i \cdot f + \sum_{i \in [l,r)} f^2 \\
= \sum_{i \in [l,r)}  a_i^2 + 2f\sum_{i \in [l,r)}a_i + \sum_{i \in [l,r)} f^2 \\
= \sum_{i \in [l,r)}  a_i^2 + 2f\sum_{i \in [l,r)}a_i + (r-l) \cdot f^2 \\
}

注意点

　上のモノイドの例は、書きやすさを重視して int にしているのでオーバーフローの危険があります。チートシートみたいに使いたい人は注意してください。

　まあ、チートシートは既に存在しますし、チートシートなしで書けるようにしよう、というのが本記事の趣旨なのでご容赦。