数独のBacktrackingによる解法

#概要
ネットに幾つか解法がありますので，無意味かもしれませんが，自己満足です．

https://news.mynavi.jp/article/zeropython-54/
での，下記の方法が一番簡単だろう
(1) 左上から右下へと順に空白マスを調べていく
(2) 空白マスがあれば、その時点で配置可能な数字を調べる
(3) 配置可能な数字を仮に配置して、次のマスを調べていく
(4) もし配置がうまくいかなければ(3)に戻る
(5) 最後のマスに到達するまで、(2)以降の処理を繰り返す
(6) 最後に到達したら結果を出力する

やっていることは，総当たりである．

例
2*2の時（ありえないが），

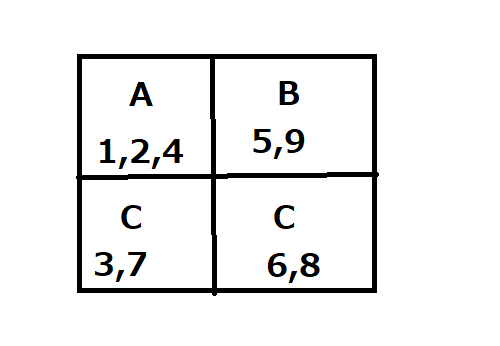
Aの場所には{1,2,4}のどれかが入るとする．このとき，

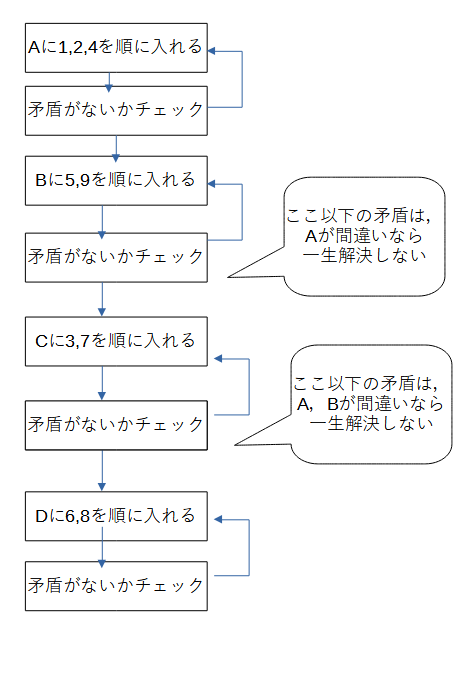
このように，A,B,C,Dの順に可能性のある数値を入れていきます．入れるたびに，矛盾がないか確認します．矛盾が発生した時点で，ほかの可能性のある数値を入れていきます．
これだけだと，各セルすべて試してダメだった時に戻らないので，すべて試してダメだった場合，ひとつ前のセルに戻らせます．

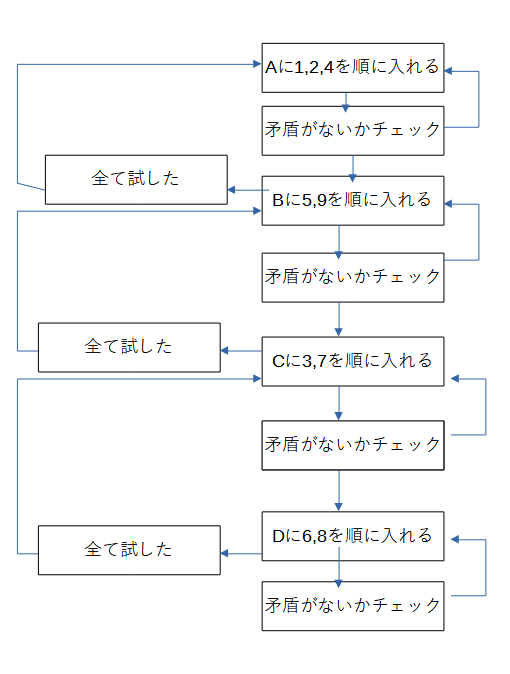
「すべて試した」「矛盾あり」で戻る場合は，そのセル以降の状態は初期状態に戻す必要があります．

#プログラム

import numpy as np		#	Numpyライブラリ
import copy


box = np.full((9,9,9),[1,2,3,4,5,6,7,8,9])

box = box.tolist()

"""
問題の定義
"""
problem = [[0,3,0,0,5,9,0,0,0],[0,5,4,0,0,0,0,9,0],[6,2,0,8,0,0,1,4,0],[4,0,0,0,0,2,0,0,8],[0,0,0,0,4,0,0,6,0],[0,0,0,1,0,6,0,0,0],[0,0,0,0,0,0,0,2,6],[0,6,0,5,0,0,0,0,0],[8,0,0,0,9,0,7,0,4]]
#0は空箱という意味

for i in range(9):
    for j in range(9):
        if problem[i][j] != 0:
            box[i][j] =[problem[i][j]]
            

            """
            可能性のある数値を除く
            """
            #列
            for k in range(9):
                if box[i][k].count(problem[i][j]) != 0 and k != j:
                    box[i][k].remove(problem[i][j])
            #行
            for k in range(9):
                if box[k][j].count(problem[i][j]) != 0 and k != i:
                    box[k][j].remove(problem[i][j])
                    
            #箱
            box_x = int(i/3)
            box_y = int(j/3)
            for x in range(3):
                for y in range(3):
                    if x + box_x*3 != i and y + box_y*3 != j:    #(i,j)での削除は除く
                        if box[x + box_x*3][y + box_y*3].count(problem[i][j]) != 0: #removeはないとエラーになるため
                            box[x + box_x*3][y + box_y*3].remove(problem[i][j])
            
            
            

        
class Cell:
    def  __init__( self,position,box,before,origin ) :
        self.position = position                     #[1,2]のような形式
        self.box = copy.deepcopy(box)                #popでのみ，変化していく
        self.before = before
        self.origin = origin
        self.result = []                             #回答が出たら，保存するための変数．
        
    def make_next_cell(self):
        while True:
            if len(self.box[self.position[0]][self.position[1]]) == 0: #popできないとき
                #beforeのインスタンスに戻る
                if self.before != -1:
                    return 0      
                    
                else:
                    #全選択肢チェック完了    (0,0)でpopできないため，これ以上はない
                    return 1
                    
                
            else:    #popできるとき
                self.box2 = copy.deepcopy(self.box)          #次のインスタンス生成用
                x = self.position[0]
                y = self.position[1]
                fixed_value = self.box[x][y].pop()  #確定値にする      
                self.box2[x][y] = [fixed_value]
                
                #check
                self.check(self.box2,self.position,fixed_value)
                
                #次の場所のインスタンスを生成する．
                x = self.position[0]
                y = self.position[1]
                if x == 8:
                    x=0
                    if y != 8:
                        y=y+1
                    else:
                        #正解が求まったことになる．　originに保存し終了
                        self.origin.result =  copy.deepcopy(self.box2)
                        return 1
                else:
                    x=x+1
                
                self.next_cell = Cell([x,y],self.box2,self,self.origin) 
                flag = self.next_cell.make_next_cell()
                
                
                if flag == 1:  #これ以上の探索は必要ない・これ以上探索できない　　 while ループを抜ける
                    break
                  
        
        
        
    def check(self,box,position,fixed_value):   #今回は，入れた数値は必ず正しく，他のセルの可能性のある数値を除く
        i = position[0]
        j = position[1]
        #列
        for k in range(9):
            if box[i][k].count(fixed_value) != 0 and k != j:
                box[i][k].remove(fixed_value)
        #行
        for k in range(9):
            if box[k][j].count(fixed_value) != 0 and k != i:
                box[k][j].remove(fixed_value)
        
        #箱
        box_x = int(i/3)
        box_y = int(j/3)
        for x in range(3):
            for y in range(3):
                if x + box_x*3 != i and y + box_y*3 != j:    #(i,j)での削除は除く
                    if box[x + box_x*3][y + box_y*3].count(fixed_value) != 0: #removeはないとエラーになるため
                        box[x + box_x*3][y + box_y*3].remove(fixed_value)
                        
    def disp(self):
        for i in range(9):
            print(origin.result[i])
        

origin =  Cell([-1,-1],box,-1,[]) 
cell = Cell([0,0],box,-1,origin)  
cell.make_next_cell()           #一つ目のセルを呼び出すことで，以降のセルもどんどん作られる

print(origin.result)

#連立方程式的解法
変数は81個
列9拘束，行9拘束，箱9拘束 で合計27個の拘束条件になります．
さらに，列，箱，行それぞれで同じ数字は入らないという拘束．これは，一つの列に対し8個の不等号拘束．よって合計8*27=216個の不等号拘束．
さらに，全変数は1~9の整数のみが入る

という問題になります．一般逆行列のような形で，等号拘束$Ax=y$から，$x=By+\alpha$の形に変形し，$By$は一定値になるので，あとは，不等号拘束・全整数1~9を成立させるように$\alpha$を探索する方法が考えられます．

表の，要素を$x_{ij}$とすると，$A$行列は

import numpy as np		#	Numpyライブラリ
import copy

A=[]


#列
for j in range(9):
    retu = []
    for i in range(81):
        if int(i/9) == j:
            retu.append(1)
        else:
            retu.append(0)
     
    A.append(retu)
    
#行
for j in range(9):
    retu = []
    for i in range(81):
        if i%9 == j:
            retu.append(1)
        else:
            retu.append(0)
            
            
    A.append(retu)

#箱
for k in range(3):
    for m in range(3):
        retu = []
        for i in range(81):
            x=i%9
            y=int(i/9)
            
            if int(x/3) == k and int(y/3):
                retu.append(1)
                
            else:
                retu.append(0)
        
        A.append(retu)
            
    

A=np.array(A)
invA = np.linalg.pinv(A)
    
print(A)

で計算できます．

ちょっと一般逆行列の知識が足らないので，もう少し知識を付けたら更新します．