球体の充填構造

はじめに

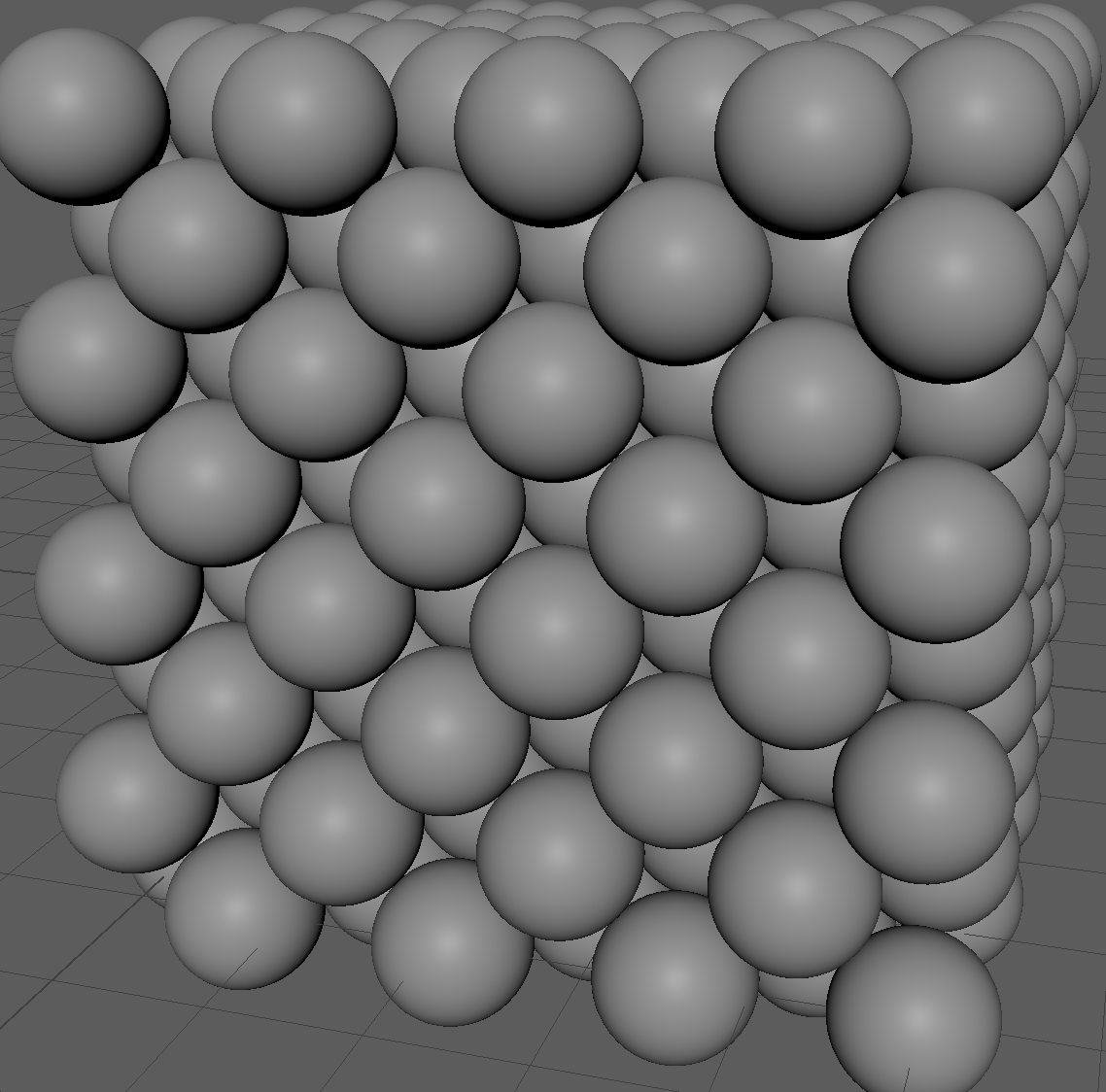
充填構造についてのメモと、Maya & MELでの配置です。
あと、元素の結晶構造についてとか。

充填構造

名称	略	英語	充填率	備考
六方最密充填構造	HCP	Hexagonal Close Packed	74
面心立方格子構造	FCC	Face Centered Cubic	74	CPPと同義
立方最密充填構造	CCP	Cubic Close Packed	74	FCCと同義
体心立方格子構造	BCC	Body Centered Cubic	68

六方最密充填構造

球を下段から順に積み重ねればいいのだが、積み重ね方によって呼び名が異なる。
１段目をそのまま３段目に持ってきた場合が、六方最密充填構造となる。

真上から見て、１段目と３段目がズレている場合、面心立方格子構造（斜めになってる）となる場合もあるし、別の配列になる場合もあるので、要注意。

パチンコ玉のような大量の球体を、適当に、ぎゅうぎゅうに並べた場合、勝手に最密充填にはなるが、並べ方を分類すると、HCPの場合もあるし、FCC(CCP)の場合もあるし、違う場合もある。

MEL

//六方最密充填構造
float $n0817 = 0.81649658092; // sqrt(2/3)=0.81649658092
float $n0577 = 0.57735026919; // 1/sqrt(3)=0.57735026919
float $n0866 = 0.86602540378; // sqrt(3)/2=0.86602540378

for ( $z = 0.0; $z < 5.0; $z += $n0866*2) {
for ( $y = 0.0; $y < 5.0; $y += $n0817*2) {
for ( $x = 0.0; $x < 5.0; $x += 1) {
    polySphere -r 0.5 -sx 60 -sy 60 -cuv 0;
    move -r $x $y $z;
}}}

for ( $z = $n0866; $z < 5.0; $z += $n0866*2) {
for ( $y = 0.0; $y < 5.0; $y += $n0817*2) {
for ( $x = 0.5; $x < 5.0; $x += 1) {
    polySphere -r 0.5 -sx 60 -sy 60 -cuv 0;
    move -r $x $y $z;
}}}

for ( $z = $n0577; $z < 5.0; $z += $n0866*2) {
for ( $y = $n0817; $y < 5.0; $y += $n0817*2) {
for ( $x = 0.0; $x < 5.0; $x += 1) {
    polySphere -r 0.5 -sx 60 -sy 60 -cuv 0;
    move -r $x $y $z;
}}}

for ( $z = $n0577+$n0866; $z < 5.0; $z += $n0866*2) {
for ( $y = $n0817; $y < 5.0; $y += $n0817*2) {
for ( $x = 0.5; $x < 5.0; $x += 1) {
    polySphere -r 0.5 -sx 60 -sy 60 -cuv 0;
    move -r $x $y $z;
}}}

setAttr "persp.translateX" 6;
setAttr "persp.translateY" 6;
setAttr "persp.translateZ" 14;
setAttr "persp.rotateX" -16;
setAttr "persp.rotateY" 16;
setAttr "persp.rotateZ" 0;

面心立方格子構造

MEL

float $n1414 = 1.41421356237; // sqrt(2)=1.41421356237

for ( $z = 0.0; $z < 5.0; $z += $n1414) {
for ( $y = 0.0; $y < 5.0; $y += $n1414) {
for ( $x = 0.0; $x < 5.0; $x += $n1414) {
    polySphere -r 0.5 -sx 60 -sy 60 -cuv 0;
    move -r $x $y $z;
}}}

for ( $z =      0.0; $z < 5.0; $z += $n1414) {
for ( $y = $n1414/2; $y < 5.0; $y += $n1414) {
for ( $x = $n1414/2; $x < 5.0; $x += $n1414) {
    polySphere -r 0.5 -sx 60 -sy 60 -cuv 0;
    move -r $x $y $z;
}}}

for ( $z = $n1414/2; $z < 5.0; $z += $n1414) {
for ( $y = $n1414/2; $y < 5.0; $y += $n1414) {
for ( $x =      0.0; $x < 5.0; $x += $n1414) {
    polySphere -r 0.5 -sx 60 -sy 60 -cuv 0;
    move -r $x $y $z;
}}}

for ( $z = $n1414/2; $z < 5.0; $z += $n1414) {
for ( $y =      0.0; $y < 5.0; $y += $n1414) {
for ( $x = $n1414/2; $x < 5.0; $x += $n1414) {
    polySphere -r 0.5 -sx 60 -sy 60 -cuv 0;
    move -r $x $y $z;
}}}

setAttr "persp.translateX" 6;
setAttr "persp.translateY" 6;
setAttr "persp.translateZ" 14;
setAttr "persp.rotateX" -16;
setAttr "persp.rotateY" 16;
setAttr "persp.rotateZ" 0;

体心立方格子構造

MEL

float $n1155 = 1.1547005; // 2/sqrt(3)=1.1547005

for ( $z = 0.0; $z < 5.0; $z += $n1155) {
for ( $y = 0.0; $y < 5.0; $y += $n1155) {
for ( $x = 0.0; $x < 5.0; $x += $n1155) {
    polySphere -r 0.5 -sx 60 -sy 60 -cuv 0;
    move -r $x $y $z;
}}}

for ( $z = $n1155/2; $z < 5.0; $z += $n1155) {
for ( $y = $n1155/2; $y < 5.0; $y += $n1155) {
for ( $x = $n1155/2; $x < 5.0; $x += $n1155) {
    polySphere -r 0.5 -sx 60 -sy 60 -cuv 0;
    move -r $x $y $z;
}}}

setAttr "persp.translateX" 6;
setAttr "persp.translateY" 6;
setAttr "persp.translateZ" 14;
setAttr "persp.rotateX" -16;
setAttr "persp.rotateY" 16;
setAttr "persp.rotateZ" 0;

元素の周期表

下記に、各元素の結晶が
・六方最密充填構造
・面心立方格子構造
・体心立方格子構造
のいずれになるか、色分けした周期表がある。

分類されていないマンガン(Mn)は、とても複雑で温度によって変化する。

	温度	単位胞あたりの原子数	構造
αマンガン	~742	58	体心立方格子類似構造
βマンガン	742~1095	20	立方晶
γマンガン	1095~1134	3	面心立方構造
δマンガン	1134~1245	1	体心立方構造

「αマンガン」やばすぎる！
https://zh.wikipedia.org/zh-cn/File:Alpha-Mn.png

ほかに、周期表の14の縦列(C,Si,Ge,Sr,Pb)には、条件によって「ダイヤモンド構造」となる性質がある。

ダイヤモンド構造 (diamond structure)西川 和弘

斜方硫黄と単斜硫黄の原子配列

ちょっと、後日、MELにしておきたい。

参考サイト

その他