Zipperというデータ構造について、図を使ってわかりやすく解説したいと思います。
この記事ではZipperがどういったものかは説明しますが、それがどう応用されうるかは紹介しません。
応用例については、少し長いですが以下の記事がわかりやすかったです。
また、ComonadとしてのZipperの応用例は、以下の記事がとてもわかりやすかったです。
コモナドを使った抽象化の威力をライフゲームで試してみた - Qiita
ただ、Haskellは遅延評価で、PureScriptは正格評価なので、この記事とは実装がところどころ異なります。
サンプルコードはPureScriptですが読めなくても図さえ見れば理解に大きな支障はないと思います。
これは余談ですが、シンタックスハイライトの関係で```haskell ... ```でコードブロック書いてるの悲しさがありますね。
Zipperとは
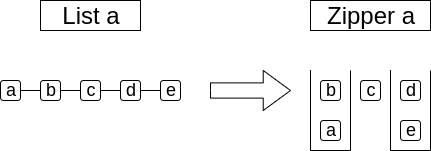
Zipperは、簡単に言うと「注目している位置」をもったデータ構造です。
今回はListのZipperについて考えます(実はList以外にもTreeのZipperなどが考えられます)。
図のように、ZipperはListのある要素に注目したデータ構造です。
上の図では、Zipper aは「List aの要素cに注目したもの」になっています。
イメージとしては、左右にスタックをもっていて、それぞれに「注目している要素より左の要素」、「注目している要素より右の要素」が積まれている、という感じです。
以下はPureScriptでの実装です。
data Zipper a = Zipper (List a) a (List a)
ここで注意ですが、Zipperの中身のListは
Zipper [a, b] c [d, e]
ではなく、
Zipper [b, a] c [d, e]
となります。
※PureScriptでは[]はListではなくArrayですが、わかりやすさのためListを[]で表現しています
これは先ほど言ったとおり、左右のListをそれぞれ「注目している要素より左の要素」「注目している要素より右の要素」のスタックとして扱っているためです。
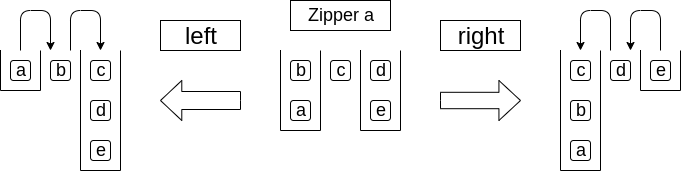
さらに、Zipperには注目している位置を変える操作としてleftとrightが存在します。
leftは1つ左の要素に、rightは1つ右の要素に注目します。
PureScriptでの実装は以下です。
left :: forall a. Zipper a -> Maybe (Zipper a)
left (Zipper Nil _ _) = Nothing
left (Zipper (l:ls) c rs) = Just (Zipper ls l (c:rs))
right :: forall a. Zipper a -> Maybe (Zipper a)
right (Zipper _ _ Nil) = Nothing
right (Zipper ls c (r:rs)) = Just (Zipper (c:ls) r rs)
left、rightはそれぞれ左端、右端まできたときそれ以上移動できず失敗するので、Maybeで表現しています。
ZipperはComonad
実はZipperはComonadになります。
Comonadの正体についてはとても抽象的で説明できる自信がないので、この記事では説明しません。
Zipperという具体例を通してなんらかの理解が得られればと思います。
Comonadになるためには、以下の関数を実装する必要があります。
extract :: Comonad w => w a -> a
duplicate :: Comonad w => w a -> w (w a)
extend :: Comonad w => (w a -> b) -> w a -> w b
Control.Comonad - purescript-control - Pursuit
今はまだ全然読めなくても大丈夫です。
実は、後ほどわかりますが
duplicate = extend identity
extend f = map f <<< duplicate
となるので、duplicateとextendはどちらか片方だけ実装すれば十分です。
では、順に説明していきます。
ZipperはFunctor
Comonadであるためには、まずFunctorである必要があります。
Functorであるためには、関数mapを実装している必要があります。
map :: forall a b f. Functor f => (a -> b) -> f a -> f b
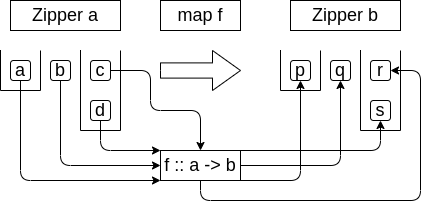
Zipperでは以下のようになります。
Zipperのmap fは、Listと同じように、中身の要素すべてにfを適用するだけです。
PureScriptでの実装は以下です。
map :: forall a b. (a -> b) -> Zipper a -> Zipper b
map f (Zipper ls c rs) = Zipper (map f ls) (f c) (map f rs)
extract
extractは、「注目している要素を取り出す」操作です。
Zipperは要素の1つに注目しているのですから、その注目している要素を取り出したくなるのは自然ですね。
extract :: forall a. Zipper a -> a
extract (Zipper ls c rs) = c
duplicate
extendは少し複雑なので、先にduplicateから説明します。
Zipperは、注目している要素をもち、またその注目している要素を移動させることができるのでしたよね。
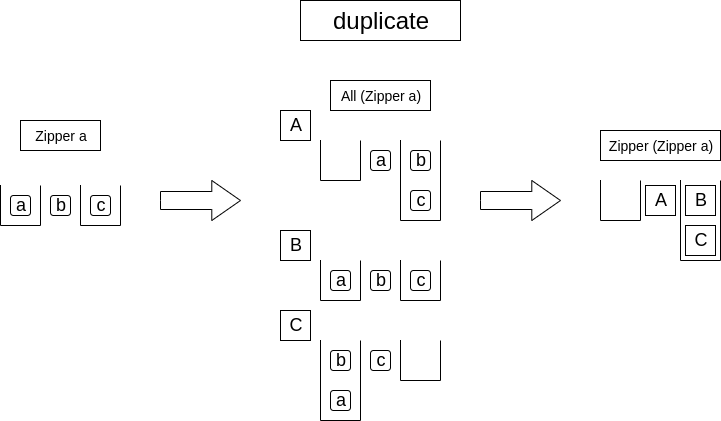
duplicateは、それぞれの要素について注目しているZipperをすべて集めてきて、さらにそれらのZipperを作ります。
A, B, Cがそれぞれ「aに注目している状態のZipper」「bに注目している状態のZipper」「cに注目している状態のZipper」ですね。
そして、それらを集めてまたZipperにしたものがZipper (Zipper a)となります。
duplicateはイメージとしては簡単なのですが、実装は少しだけ複雑になります。
iterateLeft :: forall a. Zipper a -> List (Zipper a)
iterateLeft z = iterateLeft' z Nil
where
iterateLeft' :: Zipper a -> List (Zipper a) -> List (Zipper a)
iterateLeft' z@(Zipper Nil _ _) accum = z : accum
iterateLeft' z@(Zipper (l:ls) c rs) accum =
iterateLeft' (z : accum)
(Zipper ls l (c:rs))
iterateRight :: forall a. Zipper a -> List (Zipper a)
iterateRight z = iterateRight' z Nil
where
iterateRight' z@(Zipper ls c Nil) accum = z : accum
iterateRight' z@(Zipper ls c (r:rs)) accum =
iterateRight' (z : accum)
(Zipper (c:ls) r rs)
duplicate :: forall a. Zipper a -> Zipper (Zipper a)
duplicate z = Zipper (drop 1 $ iterateLeft z)
z
(drop 1 $ iterateRight z)
むずかしいことをしているように見えますが、やりたいことは簡単で
iterateLeft (Zipper [b, a] c [d, e])
= [ Zipper [] a [b, c, d, e]
, Zipper [a] b [c, d, e]
, Zipper [b, a] c [d, e]
]
iterateRight (Zipper [b, a] c [d, e])
= [ Zipper [d, c, b, a] e []
, Zipper [c, b, a] d [e]
, Zipper [b, a] c [d, e]
]
です。
※わかりやすさのため[]をAraryではなくListとしています
つまり、iterateLeftは「現在のZipperと、1つ左に注目したZipperと、もう1つ左に注目したZipperと、...」を集めてきて、それらをListにして返します。
iterateRightも同様に、「現在のZipperと、1つ右に注目したZipperと、もう1つ右に注目したZipperと、...」を集めたListを返します。
duplicateでは、それらを使ってそれぞれの要素に注目したZipper全体のZipperを作っています。
iterateLeftとiterateRightをそのまま使うと現在のZipperが被るので、duplicateの中でそれらの返り値を1つのZipperにするとき**drop 1で現在のZipperを落としています**。
もしdrop 1をせず
duplicate (Zipper [b, a] c [d, e])
= Zipper
(iterateLeft (Zipper [b, a] c [d, e])
(Zipper [b, a] c [d, e])
(iterateRight (Zipper [b, a] c [d, e])
としてしまうと、
Zipper [C, B, A] C [C, D, E]
A = Zipper [] a [b, c, d, e]
B = Zipper [a] b [c, d, e]
C = Zipper [b, a] c [d, e]
D = Zipper [c, b, a] d [e]
E = Zipper [d, c, b, a] e []
となってしまい、Cが3つもあることになります。
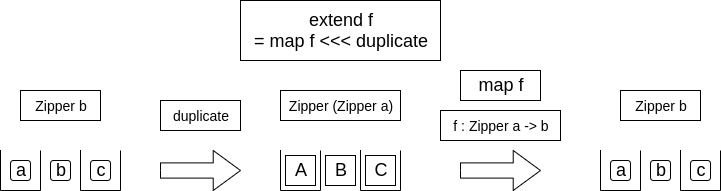
extend
extendは少し複雑だと言いましたよね。
その理由は2つの処理を一度に行っているからです。
そしてその2つというのが、**mapと、先ほどのduplicate**です。
つまり、最初に少し触れたとおり
extend f = map f <<< duplicate
となります。もう少し丁寧に書くと
extend f z = map f (duplicate z)
ですね。
これが本当なのかは、型を見てみると良いです。
map :: (a -> b) -> w a -> w b
duplicate :: w a -> w (w a)
extend :: (w a -> b) -> w a -> w b
f :: w a -> b
extend f :: w a -> w b
map f :: w (w a) -> w b -- map の型について a = w a と見る
map f <<< duplicate :: w a -> w b
extend f = map f <<< duplicate
exten fはmap f <<< duplicateになりそうですね。
つまり、extend fは**duplicateしてから、その各要素にfを適用します(map f)**。
duplicateのときと同様に、A, B, Cがそれぞれ「aに注目している状態のZipper」「bに注目している状態のZipper」「cに注目している状態のZipper」です。
そしてextendはf :: Zipper a -> bという関数を受け取るので、最終的な出力はZipper bになります。
PureScriptでの実装は以下です。
extend :: forall a b. (Zipper a -> b) -> Zipper a -> Zipper b
extend f = map f <<< duplicate
-- または
extend f z = map f (duplicate z)
まとめ
ここまでで、Zipperがどういったデータ構造で、またどのようにComonadとなるのかがわかったと思います。
今回はListのZipperがComonadになることを見ましたが、TreeのZipperなど他のZipperを見てみたり、他のComonadを見てみると面白いかもしれませんね。
Pursuitで色々見てみると面白いかもしれません。
Data.Tree - purescript-tree - Pursuitなんて言うのがありますが、Treeの実装にCofreeを使っているので、先にCofreeをやらないと少し読みづらいですね。
そのうちCofreeでTreeをつくる記事とか書いてみたいです。
さらっとだけ言うと、FreeはFunctorからMonadが作れ、CofreeはFunctorからComonadがつくれます。
言ってませんでしたが、TreeはそのZipperだけでなく、それ自体もComonadになれます。
ちなみにCofreeと関係のあるFreeに関しては以下の記事がわかりやすかったです。
そろそろFreeモナドに関して一言いっとくか - モナドとわたしとコモナド
この方のブログは大変わかりやすく、とてもお世話になりました。
おまけ1:PureScriptでの実装コード全文
PureScriptではComonadをより抽象化したExtendが定義されています。
また、今回はわかりやすさのためextendをduplicateを使って実装しました。
ただ、PureScriptではduplicateはControl.Comonadで
duplicate :: forall a w. Extend w => w a -> w (w a)
duplicate = extend identity
と実装されているので、直接extendを実装しています。
詳しくはPursuitで見てみてください。
Control.Comonad - purescript-control - Pursuit
module Data.List.Zipper where
import Prelude
import Control.Comonad (class Comonad)
import Control.Extend (class Extend)
import Data.List (List(..), (:), drop)
import Data.Maybe (Maybe(..))
data Zipper a = Zipper (List a) a (List a)
left :: forall a. Zipper a -> Maybe (Zipper a)
left (Zipper Nil _ _) = Nothing
left (Zipper (l:ls) c rs) = Just $ Zipper ls l (c:rs)
right :: forall a. Zipper a -> Maybe (Zipper a)
right (Zipper _ _ Nil) = Nothing
right (Zipper ls c (r:rs)) = Just $ Zipper (c:ls) r rs
instance functorZipper :: Functor Zipper where
map f (Zipper ls c rs) = Zipper (map f ls) (f c) (map f rs)
iterateLeft :: forall a. Zipper a -> List (Zipper a)
iterateLeft = flip go Nil
where
go z@(Zipper Nil _ _) accum = z : accum
go z@(Zipper (l:ls) c rs) accum = go (Zipper ls l (c:rs)) (z : accum)
iterateRight :: forall a. Zipper a -> List (Zipper a)
iterateRight = flip go Nil
where
go z@(Zipper _ _ Nil) accum = z : accum
go z@(Zipper ls c (r:rs)) accum = go (Zipper (c:ls) r rs) (z : accum)
instance extendZipper :: Extend Zipper where
extend f z = Zipper (map f $ drop 1 $ iterateLeft z) (f z) (map f $ drop 1 $ iterateRight z)
instance comonadZipper :: Comonad Zipper where
extract (Zipper _ c _) = c
おまけ2:ComonadとMonad
Comonadは“Co”monadというくらいですから、Monadと関係があります。
実際ComonadとMonadは**双対(dual)**になります。
ここではComonadとMonadの間にどういった関係があるのか、簡単なイメージを説明します。
型の対応
ComonadとMonadの対応を、それぞれの型を見ることで考えてみます。
まず、ComonadとMonadがそれぞれ実装する必要のある関数を見ます。
-- Monad
pure :: forall a m. Monad m => a -> m a
join :: forall a m. Monad m => m (m a) -> m a
bind :: forall a b m. Monad m => m a -> (a -> m b) -> m b
-- Comonad
extract :: forall a w. Comonad w => w a -> a
duplicate :: forall a w. Comonad w => w a -> w (w a)
extend :: forall a b w. Comonad => (w a -> b) -> w a -> w b
HaskellやPureScriptを知らない人はforall a m. Monad m =>のところが読みにくいと思いますが、とりあえずそこは無視して後ろだけ見てください。
まずpureとextractです。
pure :: a -> m a
extract :: w a -> a
mとwを読み替えれば、->が反対になっていますね。
次にjoinとduplicateを見てみます。
join :: m (m a) -> m a
duplicate :: w a -> w (w a)
これもmとwを読み替えれば、->の向きを逆にしたものになっていますね。
最後にbindとextendです。
bind :: m a -> (a -> m b) -> m b
extend :: (w a -> b) -> w a -> w b
このままではちょっとわかりづらいですね。
ということで、extendの引数の順番を変えてみます。
bind :: m a -> (a -> m b) -> m b
extend :: w a -> (w a -> b) -> w b
だいぶん見えてきましたね。
最後に、わかりやすいようextendのaとbを入れ替えてみます。
bind :: m a -> (a -> m b) -> m b
extend :: w b -> (w b -> a) -> w a
これでbindとextendも、mとwを読み替えれば**->の向きが反対なだけの関係**になりましたね。
具体例
Comonadの例としてZipperを、Monadの例としてListを考えます。
-- Monadの例(List)
pure :: forall a. a -> List a
pure x = x : Nil
join :: forall a. List (List a) -> List a
join Nil = Nil
join (xs:xss) = xs <> (join xss)
bind :: forall a b. List (List a)
bind xs f = join (map f xs)
-- Comonadの例(Zipper)
extract :: forall a. Zipper a -> a
extract (Zipper ls c rs) = c
duplicate :: forall a. Zipper a -> Zipper (Zipper a)
-- 省略
extend :: forall a b. (Zipper a -> b) -> Zipper a -> Zipper b
-- 省略
MonadとしてのList
pureは要素を1つ受け取って、それだけをもつListを作る関数ですね。
singletonという名前で定義されることがあります。
joinは、ListのListをすべて結合して1つのListにしてしまう関数です。
flattenなどと呼ばれることが多いです。
最後にbindですが、少しイメージがしづらいかもしれません。
実は、
bind xs f = join (map f xs)
となります。
型を見てみると、
map :: (a -> b) -> List a -> List b
join :: List (List a) -> List a
bind :: List a -> (a -> List b) -> List b
xs : List a
f :: a -> List b
bind xs f :: List b
map f :: List a -> List (List b) -- map の b を List b とみる
map f xs :: List (List b)
join (map f xs) :: List b
bind xs f = join (map f xs)
となり、確かにbind xs f = join (map f xs)となりそうですね。
つまり、bindはListと「要素1つを受け取ってListを返す」ような関数を受け取り、その関数をすべての要素に適用し、またその結果のListをすべて結合する、という処理になります。
ComonadとしてのZipper
extractは、Zipperが現在注目している要素を取り出す関数でしたね。
duplicateは、すべての要素についてその要素に注目したZipperをもってきて、それらのZipperを作る関数でした。
extendはduplicateとmapに分解することができて、
extend f z = map f (duplicate z)
でしたね。
なんだかMonadとしてのListで似たような説明を見た気がしますね。
対応
pure :: forall a. a -> List a
extract :: forall a. Zipper a -> a
pureは「1つの要素からListを作る」関数でした。
そして、extraxtは「Zipperから注目している要素を(1つ)取り出す」関数でしたね。
join :: forall a. List (List a) -> List a
duplicate :: forall a. Zipper a -> Zipper (Zipper a)
joinはListのListを、すべて結合して1つのListにまとめてしまう関数でした。
つまり「重なりを潰す」関数ですね。
duplicateはすべての要素について、それに注目したZipperをもってきて、それらのZipperを作る関数でしたね。
つまり、Zipperを「重ねる」関数です。
bind :: forall a b. List a -> (a -> List b) -> List b
extend :: forall a b. (Zipper a -> b) -> Zipper a -> Zipper b
bindとextendはそのままではわかりづらいですね。
ここで、bindはmapとjoin、extendはmapとduplicateで書き換えられたことを思い出します。
bind f xs = join (map f xs)
extend f z = map f (duplicate z)
bindは「それぞれの要素にf :: a -> List bを適用してから、重なりを潰す」関数ですね。
extendは「Zipperを重ねてから、それぞれの要素(Zipper)にf :: Zipper a -> bを適用する」関数となりますね。
どうでしょう、具体例を見ることで、少しだけ対応関係のイメージが掴みやすくなったでしょうか。
まとめ
こういったComonadとMonadのような、矢印の向きを反対にした関係を、圏論の用語で双対と言うそうです。
ただ、矢印は必ずしも関数というわけではありません。
説明できる自信がないのでここでは触れませんが、気になる人は圏論を学んでみると良いかもしれません。