コモナドはHaskellで実現できる圏論的な抽象化パターンのひとつです。モナドと名前に入っている通り あのモナドと密接に関係しており、圏論の世界ではモナドの双対となっています1。定義を見てみましょう。
class Functor w => Comonad w where
extract :: w a -> a
extend :: (w b -> a) -> w b -> w a
duplicate :: w a -> w (w a)
duplicate = extend id
extend f = fmap f . duplicate
モナドの定義と見比べてみると、
class Functor m => Monad m where
return :: a -> m a
(>>=) :: (a -> m b) -> m a -> m b
join :: m (m a) -> m a
join = (>>= id)
k >>= m = join $ fmap k m
extract は return と、extend は >>= と、duplicate は join と、それぞれなんとなく反対になってるような気がしますよね?(m と w も上下反対の対応がありますねw)
コモナドの感覚を掴むために具体的な実装を見てみましょう。
-- | List Zipper
data Z a = Z [a] a [a]
left, right :: Z a -> Z a
left (Z (l:ls) c rs) = Z ls l (c:rs)
right (Z ls c (r:rs)) = Z (c:ls) r rs
iterate1 :: (a -> a) -> a -> [a]
iterate1 f = tail . iterate f
instance Functor Z where
fmap f (Z ls c rs) = Z (fmap f ls) (f c) (fmap f rs)
instance Comonad Z where
extract (Z _ a _) = a
duplicate z = Z (iterate1 left z) z (iterate1 right z)
extend f z = Z (fmap f $ iterate1 left z) (f z) (fmap f $ iterate1 right z)
これはZipperと呼ばれているデータ構造で、特にListのZipperとなっています。Zipperはデータ全体と注目している要素の2つを併せ持つデータ構造で、すごいH本でも紹介されています。
イメージとしては Z [a] a [a] は以下のようになっていて、一本のリストの中にある途中の要素に注目している形になっています。left や right を使えば注目している場所を左右に動かすことができるという寸法です。

このZipperのコモナドの実装を見てみると、extractは注目している値を返していて、duplicateは注目する場所を左右にずらした全てのZipperを集めたZipperになっています。イメージにすると以下のような感じです。
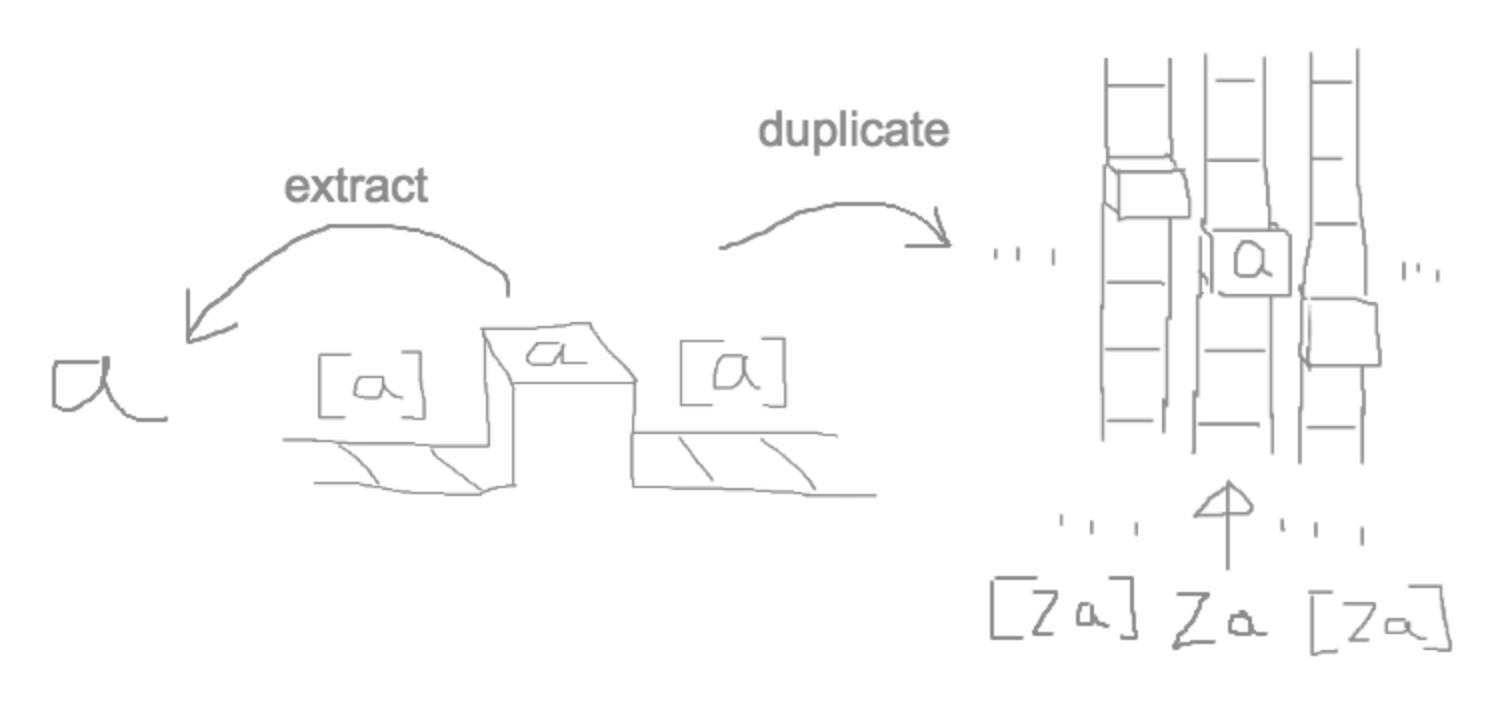
コモナドにはZipper以外にもStreamやStoreなどたくさんのインスタンスがあり、どれもとても便利なものです2。Zipperは特にコモナドと縁が深く、コモナドはZipperの一般化になっているようです3。
それではコモナドを使うことによってどのような恩恵を受けることができるのか、実際にライフゲームを作りながら試してみましょう。ライフゲームは2次元の盤面上で発展していくので先ほどのZを組み合わせて2次元のデータ構造を作ります。
newtype Z2 a = Z2 (Z (Z a))
instance Functor Z2 where
fmap f (Z2 zz) = Z2 (fmap (fmap f) zz)
instance Comonad Z2 where
extract (Z2 zz) = extract (extract zz)
duplicate (Z2 zz) = fmap Z2 . Z2 . roll $ roll zz where
roll zz = Z (iterate1 (fmap left) zz) zz (iterate1 (fmap right) zz)
roll は2重になったZipperの内側を左右にずらしたものを集めてより大きなZipperを作っています。
- 生きているマスは隣接しているマスの中で生きているマスが2個もしくは3個であれば次のターンも生きている
- 死んでいるマスは隣接しているマスの中で生きているマスがちょうど3個であれば次のターンで生きているマスになる
- それ以外の場合は次のターンで死んでいるマスになる
というルールで2次元のマスを発展させていくものです。これをZ2 Boolを使って実装すると
countNeighbours :: Z2 Bool -> Int
countNeighbours (Z2 (Z
(Z (n0:_) n1 (n2: _):_)
(Z (n3:_) _ (n4:_))
(Z (n5:_) n6 (n7: _):_))) =
length $ filter id [n0, n1, n2, n3, n4, n5, n6, n7]
life :: Z2 Bool -> Bool
life z = (a && (n == 2 || n == 3)) || (not a && n == 3) where
a = extract z
n = countNeighbours z
のように書くことが出来ます。Z2 BoolはZipperなので注目している場所があってcountNeighboursがスッキリ書けていますね。
そして、 lifeを使うとZ2 Boolを1ステップ発展させる関数は
extend life
と書くことが出来ます。 これがコモナドの威力です! countNeighboursとlifeはどちらも1つの点の振る舞いについて記述しているだけですがこれをextendを使って全体を発展させる処理に簡単に変換することが出来ました。for文で走査しながら変更していく処理を記述する手間が全く無くなりましたね!
extend lifeがやっていることは以下のようなイメージです。duplicateによって全ての点に注目するZ2を複製してそれをfmap lifeで各点で集約して並べたものを作っています。こんな計算をしても遅延評価があるおかげで計算量が無限になってしまうことはありません。

あとはlifeを繰り返し適用して表示する機能を実装すれば以下のようにライフゲームを作ることが出来ます。
実はZ2は無限に広がる2次元の盤面を表現しているのでこのライフゲームは無限の盤面上の発展をシミュレーションできています。しかし時間が経つに連れて考慮するマスがどんどん増えていくのでどんどん重くなってきてしまいます。トーラスの上でライフゲームを考えればこの問題はなくなりそうです。トーラス上のZipperを定義してこの問題を解決するのはとても面白そうな演習なので気になった人は是非やってみて下さい!
最後に今回実装したライフゲームの全てのコードを載せて終わりたいと思います。
import Control.Monad (replicateM_)
import Control.Concurrent (threadDelay)
import Data.List (intercalate)
---------------------------
-- Comonad
---------------------------
class Functor w => Comonad w where
extract :: w a -> a
extend :: (w b -> a) -> w b -> w a
duplicate :: w a -> w (w a)
duplicate = extend id
extend f = fmap f . duplicate
---------------------------
-- List Zipper
---------------------------
data Z a = Z [a] a [a]
left, right :: Z a -> Z a
left (Z (l:ls) c rs) = Z ls l (c:rs)
right (Z ls c (r:rs)) = Z (c:ls) r rs
iterate1 :: (a -> a) -> a -> [a]
iterate1 f = tail . iterate f
instance Functor Z where
fmap f (Z ls c rs) = Z (fmap f ls) (f c) (fmap f rs)
instance Comonad Z where
extract (Z _ a _) = a
duplicate z = Z (iterate1 left z) z (iterate1 right z)
extend f z = Z (fmap f $ iterate1 left z) (f z) (fmap f $ iterate1 right z)
toZ :: a -> [a] -> Z a
toZ a xs = Z (repeat a) a (xs ++ repeat a)
---------------------------
-- 2D List Zipper
---------------------------
newtype Z2 a = Z2 (Z (Z a))
instance Functor Z2 where
fmap f (Z2 zz) = Z2 (fmap (fmap f) zz)
instance Comonad Z2 where
extract (Z2 zz) = extract (extract zz)
duplicate (Z2 zz) = fmap Z2 . Z2 . roll $ roll zz where
roll zz = Z (iterate1 (fmap left) zz) zz (iterate1 (fmap right) zz)
toZ2 :: a -> [[a]] -> Z2 a
toZ2 a xss = Z2 $ toZ (toZ a []) (map (toZ a) xss)
---------------------------
-- Life Game
---------------------------
countNeighbours :: Z2 Bool -> Int
countNeighbours (Z2 (Z
(Z (n0:_) n1 (n2: _):_)
(Z (n3:_) _ (n4:_))
(Z (n5:_) n6 (n7: _):_))) =
length $ filter id [n0, n1, n2, n3, n4, n5, n6, n7]
life :: Z2 Bool -> Bool
life z = (a && (n == 2 || n == 3)) || (not a && n == 3) where
a = extract z
n = countNeighbours z
showZ2 :: Int -> Int -> Z2 Char -> IO ()
showZ2 w h (Z2 (Z _ _ rows)) = do
flip mapM_ (take h rows) $ \(Z _ _ row) -> do
putStrLn . intercalate " " . map pure $ take w row
main :: IO ()
main = do
let c2b c = if c == ' ' then False else True
b2c b = if b then '#' else ' '
(w, h) = (10, 10)
field = [ " # "
, " #"
, "###"
]
initState = fmap c2b $ toZ2 ' ' field
loop state = do
let state' = extend life state
replicateM_ h $ putStr "\ESC[A\ESC[2K" -- clear terminal
showZ2 w h (fmap b2c state)
threadDelay 300000
loop state'
replicateM_ h $ putStrLn ""
loop initState