皆さんご存じのUnionFind。
使い方は知っていても中身の仕組みを知らないと思います(というか自分があまり知らない)
中身の仕組みが知らないとUnionFindの改造もできません
という事で色々調べてみます
UnionFindの基本的な機能
どんなことができるかを一応書きます
グラフを連結させるのと頂点同士が連結になっているかを調べることができます
つまりグループ分けすることと同じグループにいるか判定することができます
最初は{0},{1},{2},{3},{4},{5}と全てバラバラでunite(1,2)を使うことで
{0},{1,2},{3},{4},{5}とまとめることができます
グラフの連結の判定や閉路検出、グリッド問題とかでよく出てきますね
最小全域木(クラスカル法)でも使いますね
UnionFindの流れ
何が起きているかを見てみましょう
こんな感じでグラフがあります

二つのグラフが連結するときは一方からもう一方に有向辺を作る感じです
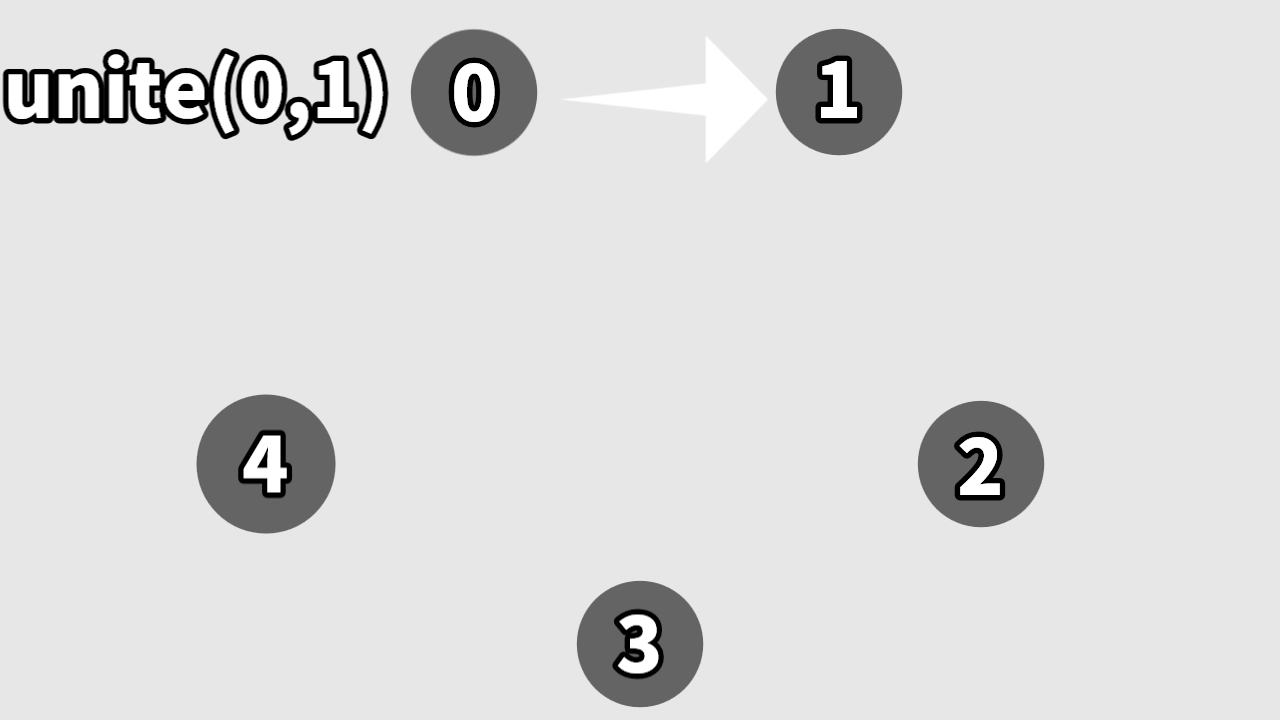
ただし指定された番号の頂点をそのままつなぐわけではありません
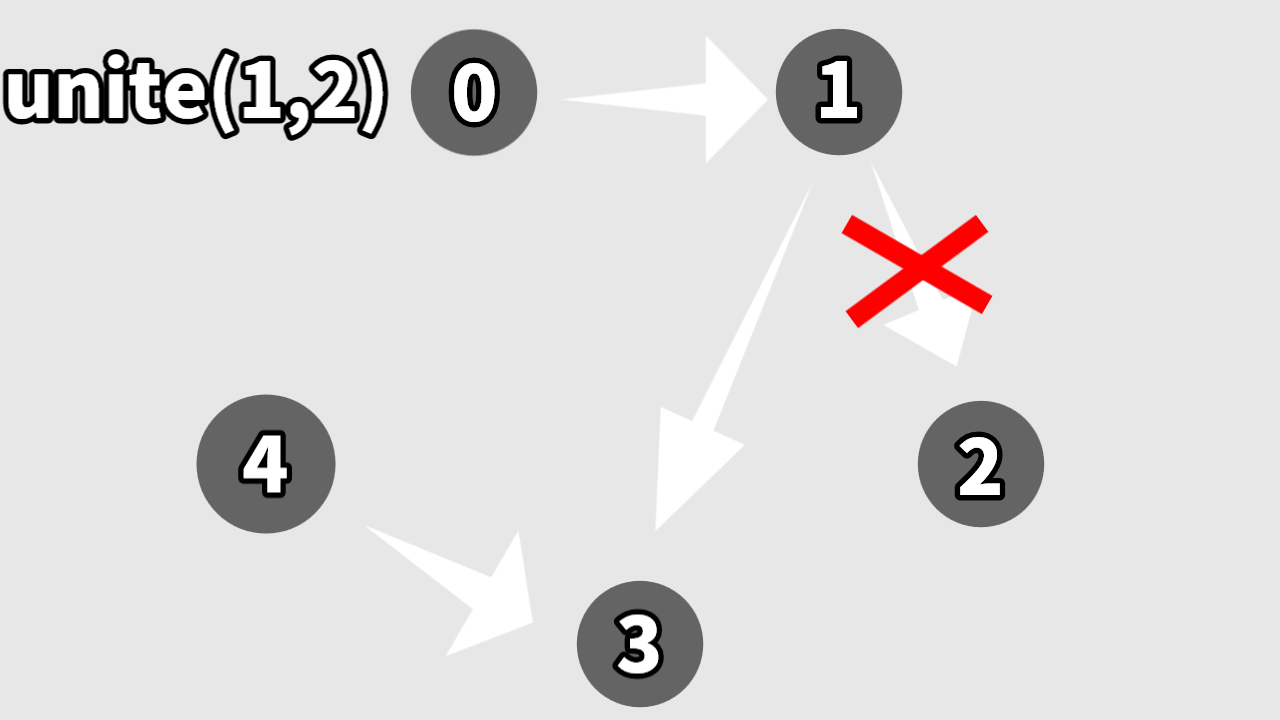
グラフを連結するとき、指定された頂点の根同士をつなぎます
根とは何か?その頂点から辺をたどって行き着く先です
例えば頂点0の根は0→1→3と辿って3となります
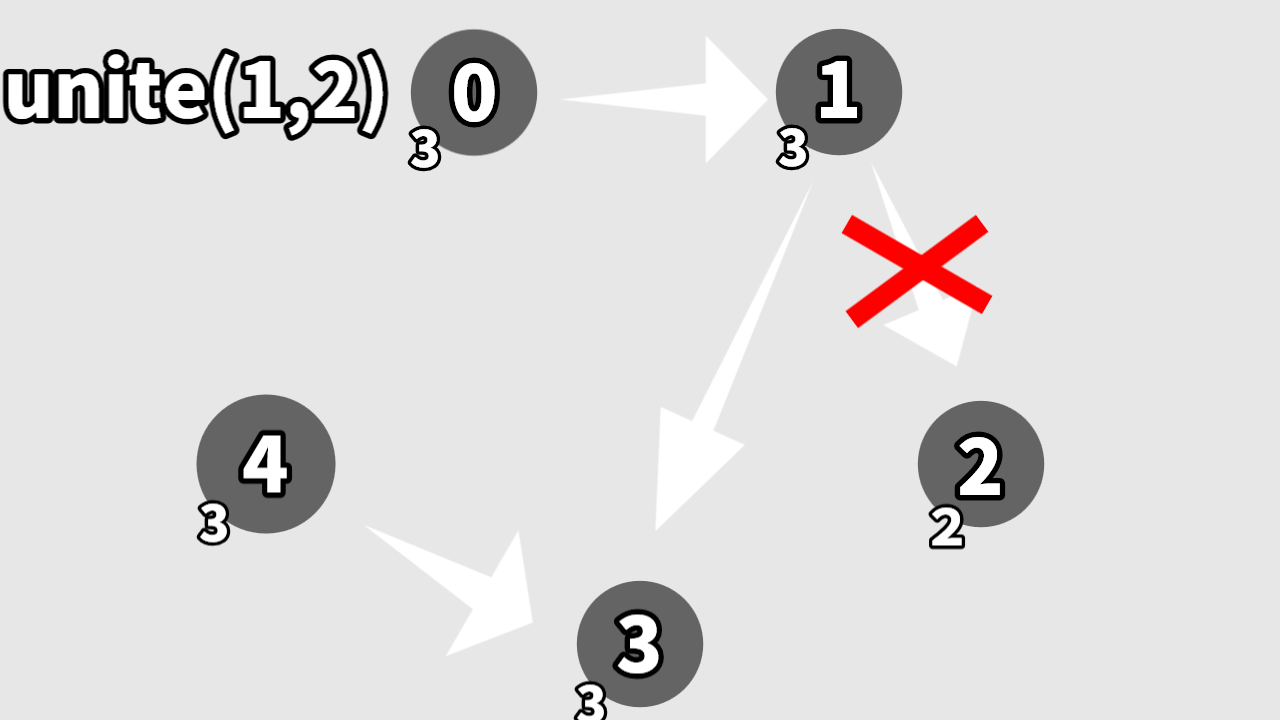
unite(1,2)だとこういう風になります
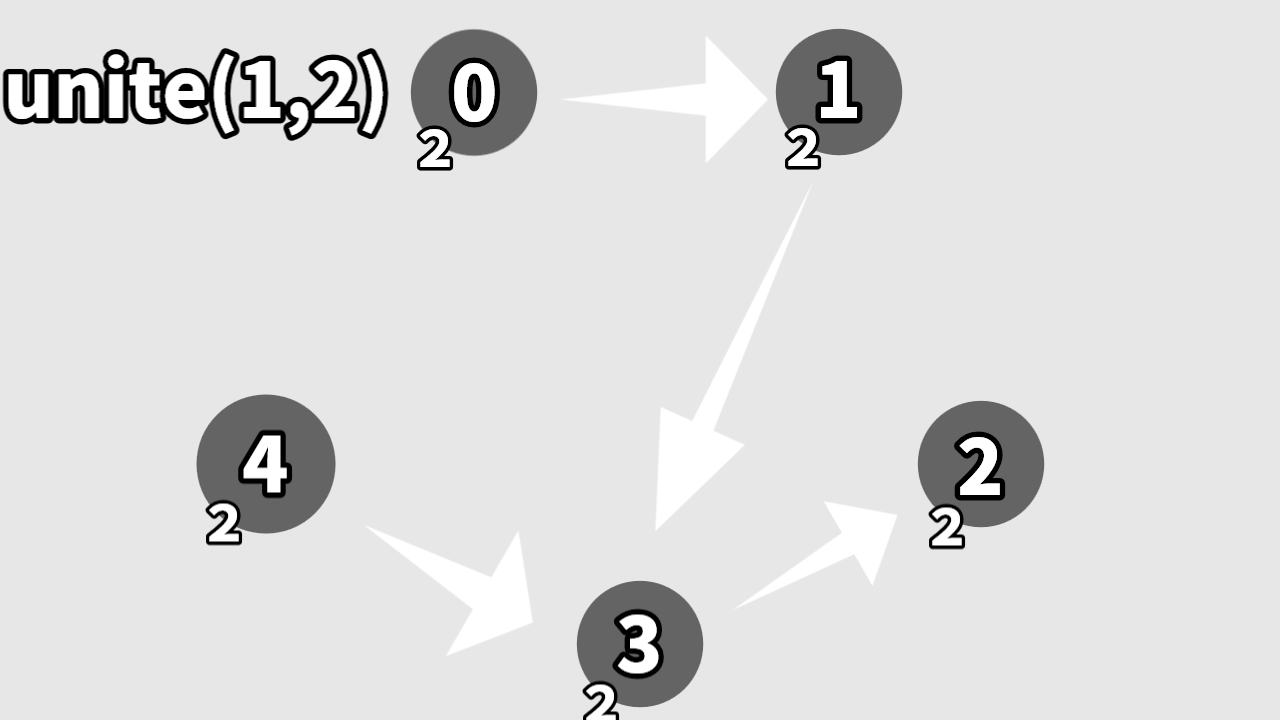
根同士をつなぐと閉路ができず、根が同じ頂点は連結されてる頂点になって、連結の判定ができます
根をたどるのも計算量がとても小さくO(a(N))です。Nは頂点数、aアッカーマン関数の逆関数とかいうよくわからないものです。実質O(1)とみなせるくらい小さいらしいです
改造してみる
たまにUnionFindを改造しないと解けない問題が出てきます
連結している頂点の番号を持たないといけなかったり、辺数を調べないといけなかったりします。
こういう問題をどう解けばいいかというと頂点に新しい情報を持てばいいです
今回は連結している頂点の数を調べていきましょう
まず、グラフを作ります。左下が根の番号で、右下が連結頂点の数です。

二つの頂点をつなげるときは根の頂点同士をつなげます
この時に、頂点数を根にする方に足します。根にしなかった方は念のため初期化しときましょう
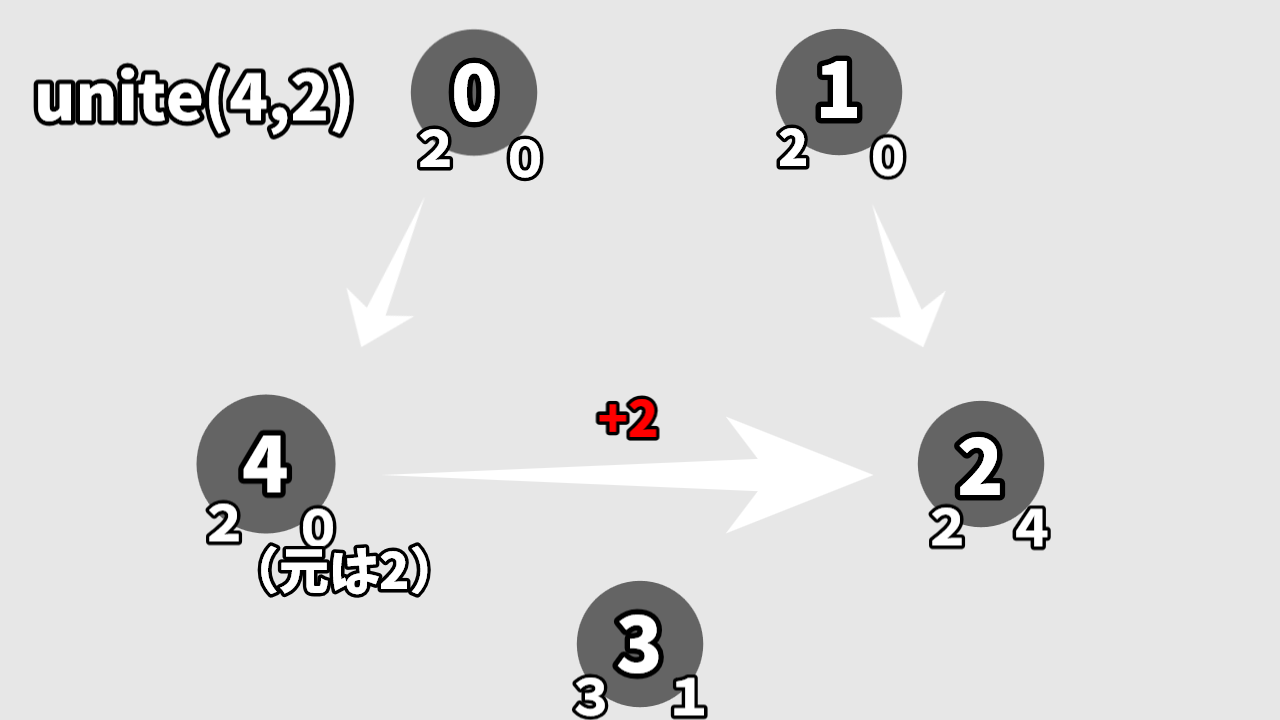
頂点数が知りたいときは指定した頂点から根をたどってそこの頂点数を持ってくればよいです
おわり
例題を置きます
https://atcoder.jp/contests/abc292/tasks/abc292_d
https://atcoder.jp/contests/abc372/tasks/abc372_e
ここまで読んでくださりありがとうございます
よくわかんないことあったらコメントしてください