右から読んでも左から読んでも変わらないもの

どうも、文字列大好き @hdbn です。

「今日は12月21日なので回文の話か！」と期待した方には申し訳ありません。違う話をします。今回は色々な文字列処理アルゴリズムによく使われる二つの重要な配列: $\mathit{LCP}$ 配列 と $\mathit{LPF}$ 配列 を紹介したいと思います。今回は時間がなかったせいで、あまり親切な文章になっていないと思いますが、分かりにくいところなどがあればなるべく補足説明を追加しますので気軽にご指摘ください。

接尾辞配列、接尾辞の逆配列

紹介したい2つの配列は皆が大好きな 接尾辞配列 (Suffix Array) に関係しているのでまずはその定義から始めます。

定義(接尾辞配列)
長さ $n$ の文字列 $T$ の接尾辞配列 $\mathit{SA}[1..n]$ は、${1,...,n}$ の順列であり、任意の $1 \leq i\leq n$ に対して $\mathit{SA}[i] = j$ は $T[j..n]$ が辞書式順序¹で $i$ 番目に小さい接尾辞であることを示す。また、接尾辞配列の逆配列 $\mathit{rank}[1..n]$ はすべての $1 \leq i \leq n$ に対して $\mathit{rank}[SA[i]] = i$ を満たす配列である。

接尾辞配列は索引構造の一つです。文字列 $T$ とその接尾辞配列があれば、辞書式順序でソートされた接尾辞にアクセスできるので、接尾辞配列上の２分探索を使うことで任意の文字列 $P$ を接頭辞として持つ $T$ の接尾辞すべて(すなわち $T$ 中の $P$ の出現すべて)を $O(|P|\log |T| +\mathit{occ})$ 時間で求めることができます。ここで、$\mathit{occ}$ は $P$ の $T$ 中の出現回数です。ちなみに、$P$ を接頭辞に持つ $T$ の接尾辞は、接尾辞配列上の連続した区間になり、その区間の長さが $\mathit{occ}$ になります。区間を見つけるのに $O(|P|\log |T|)$ 時間、区間の全要素を出力するのに$O(\mathit{occ})$ 時間、といった感じです。

LCP 配列

次に、紹介したい 1 目の配列、$\mathit{LCP}$ (Longest Common Prefix) 配列を定義します。

定義(LCP 配列)
長さ $n$ の文字列 $T$ の $\mathit{LCP}[1..n]$ 配列とは、次のように定義される配列である。

$\mathit{LCP}[1] = 0$、また、任意の $2 \leq i \leq n$ に対して
$\mathit{LCP}[i] =\mathit{lcp}(T[\mathit{SA}[i-1]..n], T[\mathit{SA}[i]..n])$

ただし、$\mathit{SA}$ は $T$ の接尾辞配列、$\mathit{lcp(x,y)}$ は文字列 $x,y$ の最長共通接頭辞の長さを表す。

つまり、$\mathit{LCP}$ 配列の $\mathit{LCP}[i]$ には、辞書式順序が $i$ 番目の接尾辞と辞書式順序が $i-1$ 番目の接尾辞の最長共通接頭辞の長さが格納されています。以下に例を示します。

例えば、$\mathit{LCP}[6] = 2$ となっているのは、辞書式順序が 6 番目の接尾辞「ナドーナードーナー」と、辞書式順序が 5 番目の接尾辞「ナドナドーナードーナー」の最長共通接頭辞が「ナド」で、その長さが 2 だからです。

ちなみに、$\mathit{LCP}$ 配列は、接尾辞配列があれば線形時間で求めることができます²。以下に疑似コードを示します。

線形時間LCP計算の擬似コード

std::vector<int> calcLCP(const std::string & T, const std::vector<int> & SA){
  int lcp = 0, n = T.size();
  std::vector<int> LCP(n), rank(n); // それぞれ大きさ n の配列
  for(int i = 0; i < n; i++) rank[SA[i]] = i;
  for(int p = 0; p < n; p++){
    int i = rank[p]; // SA[i] = p
    if(i > 0){
      while(T[p+lcp] == T[SA[i-1]+lcp]) lcp++;
    } else {
      lcp = 0;
    }
    LCP[i] = lcp;
    if(lcp > 0) lcp--;
  }
  return LCP;
}

何故これで正しく計算できているかは、簡単に言うと、**「任意の接尾辞 $T[p..n]$ の対応する位置での $\mathit{LCP}$ の値は、1 文字短い接尾辞 $T[p+1..n]$ の対応する位置での $\mathit{LCP}$ の値よりも高々 1 大きい」**という性質 (数式で書くと $\mathit{LCP}[\mathit{rank}[p+1]] \geq \mathit{LCP}[\mathit{rank}[p]] - 1$) が成り立つからです。計算量は、for 文の中に while 文があって二重ループとなっていますが、lcp の最大値が $n$ であることと、for 文の中で lcp が高々1つずつしか減らないため、while 文の実行が全体で $O(n)$ 回で収まり $O(n)$ 時間となります。

$\mathit{LCP}$ 配列は、接尾辞木と接尾辞配列をつなぐための情報と考えることもできて、接尾辞木中の内部接点の根からの深さ(パスラベル長)に対応します。接尾辞配列と $\mathit{LCP}$ 配列を使うと、接尾辞木を明示的に作らずとも、後置順の走査が可能になったり²と、色々な使い方があります。

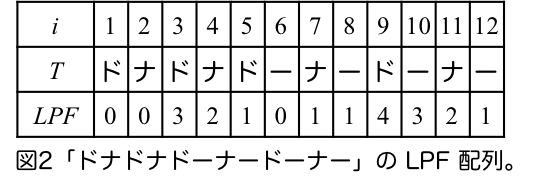
LPF 配列

次に、$\mathit{LPF}$ (Longest Previous Factor) 配列を定義します。

定義(LPF 配列)
長さ $n$ の文字列 $T$ の $\mathit{LPF}[1..n]$ 配列とは、すべての $1 \leq i \leq n$ に対して、次のように定義される配列である。

$\mathit{LPF}[1] = 0$、また、任意の $2 \leq i \leq n$ に対して
$\mathit{LPF}[i] = \max\{ \mathit{lcp}(T[i..n], T[j..n]) \mid 1 \leq j < i \}$

つまり、$\mathit{LPF}[i]$ は位置 $i$ から始まる接尾辞 $T[i..n]$ と $i$ 未満の任意の位置 $j$ から始まる接尾辞 $T[j..n]$ の最長共通接頭辞の長さの最大値です。別の言い方をすると $\mathit{LPF}[i]$ は、位置 $i$ から始まる $T$ の部分文字列のうち、位置 $i$ より前に出現する最長のものの長さです。以下に例を示します。

例えば、$\mathit{LPF}[3] = 3$ となっているのは、$T[3..n]$ の接頭辞でかつ $3$ 未満の位置から開始する接頭辞との最長共通接頭辞で最長なものは、$T[2..n]$ との最長共通接頭辞の「ドナド」でありその長さが $3$ だからです。
$\mathit{LPF}$ 配列は、接尾辞配列があれば線形時間で求めることができます。計算方法は幾つかありますが、あまり簡単に記述できなさそうだったので説明は割愛します。なお、$\mathit{LPF}$ 配列があると、圧縮で有名な LZ77分解 を簡単に計算することができるようになります。(本当は長さだけでなく、対応する位置 $j$ も計算しておかないとあまり面白いことができないのですが、今回は説明を割愛します)

LPF配列を用いたLZ77分解の計算(LZ77分解の項の長さの列を出力)

// ちょっと手抜きですみません
p = 0;
while(p < n){
  l = max(1, LPF[p]);
  output(l);
  p += l;
}

LCP 配列と LPF 配列の関係

さて、導入が少し長かったですが、ここからがいよいよ本題です。$\mathit{LCP}$ 配列と $\mathit{LPF}$ 配列の間には次のような面白い関係があります。

定理1
文字列 $T$ の $\mathit{LCP}$ 配列の全要素の多重集合は文字列 $T$ の $\mathit{LPF}$ 配列の全要素の多重集合と等しい。

つまり、$\mathit{LCP}$ 配列を並び替えて $\mathit{LPF}$ 配列が得られる、ということです。俄かには信じがたいですが、先の例を見てみましょう。図1と図2を見ると「ドナドナドーナードーナー」の $\mathit{LCP}$ 配列と $\mathit{LPF}$ 配列はどちらも

$0$ が 3 つ、$1$ が 4 つ、$2$ が 2 つ、$3$ が 2 つ、$4$ が 1 つ

からなっていて、一致します。マジっぽい！ ということで、証明を考えてみましょう。

証明
もうすこし一般的なことを証明します。長さ $n$ の文字列 $T$ と任意の $[1..n]$ の順列 $\pi = (\pi_1, \ldots, \pi_n)$ によって定義される次の配列

$L_\pi[1] = 0$、また、任意の $2\leq i < n$ に対して
$L_\pi[i] = \max \{ \mathit{lcp}(T[\pi_i..n], T[\pi_j..n]) \mid 1 \leq j < i\}$

の要素の多重集合が $\pi$ に依らず等しいことを示します。ちょっと考えると、$\pi = (1,\ldots n)$ としたのが $\mathit{LPF}$ 配列に対応することが分かると思います。また、$\pi = (\mathit{SA}[1], \ldots, \mathit{SA}[n])$ とすると $\mathit{LCP}$ 配列に対応しています。$\mathit{LCP}$ 配列の定義には $\max$ が出てきておらず、ちょっと違うのでは、と思うかもしれませんが、辞書式順序で並んでいれば辞書式順序が1つ前の接尾辞との $\mathit{lcp}$ が最大値を取るため、同じことになります。以上のことから、この命題が証明できれば、定理1が示せることになります。

接尾辞木を構築するアルゴリズムとして (計算効率は考えず)、$\pi$ の順に接尾辞を1つずつ追加して構築することを考えます。ある接尾辞 $T[\pi_i..n]$ を追加するとき、途中まで構築された接尾辞木の根から $T[\pi_i..n]$ で辿れるだけ辿り、辿れないところで必要であれば頂点を追加し、枝分かれさせて新たな葉を作る、という操作を繰り返すことで接尾辞木を構築することができます。この際に枝分かれする時の根からのパス長が $L_\pi[i]$ に対応します。このため、最終的な $L_\pi$ の要素の多重集合に対し、各頂点 $v$ からは、その子の数を $c_v$ とすると、$v$ のパスラベル長 $c_v-1$ 個の寄与があります。一方でこのアルゴリズムで作られる接尾辞木は任意の順列 $\pi$ に対して同じ形になるため、$\pi$ によらず $L_\pi$ の要素の多重集合は等しくなります。(証明終わり)

これだけでもまぁまぁ面白いのですが、驚くのはまだ早いです！ 更に次のような関係が成り立ちます。

定理2³
文字列 $T$ の逆文字列を $T^R$ とする (任意の $1 \leq i \leq |T|$ に対して $T^R[i] = T[|T|-i+1]$)。文字列 $T$ の LCP 配列の全要素の多重集合は、文字列 $T^R$ の LCP 配列の全要素の多重集合と等しい。

幾ら何でも嘘でしょう。例を考えてみましょう。

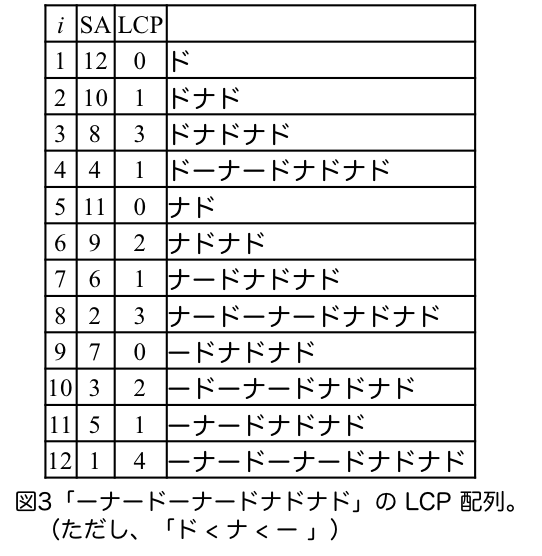
図3を見ると、「ドナドナドーナードーナー」の逆文字列「ーナードーナードナドナド」の $\mathit{LCP}$ 配列には やはり

$0$ が 3つ、$1$ が 4つ、$2$ が 2つ、$3$ が2つ、$4$ が1つ

あり、一致します！ マジだった！ ということで、証明を考えてみましょう。

証明
まず、任意の $1 \leq k\leq n$ に対して、値が $k$ 未満になる $\mathit{LCP}$ 配列の要素が幾つかあるか、というのを数えてみます。接尾辞の長さが $k$ 未満であれば、対応する $\mathit{LCP}$ の値は当然 $k$ 未満になります。そのような、長さが $k$ 未満の接尾辞は $k-1$ 個あります。次に、長さが $k$ 以上の接尾辞について考えます。文字列 $T$ のある長さ $k$ の部分文字列 $P$ を考えると、先に述べたように $P$ を接頭辞として持つ接尾辞は接尾辞配列上の区間に対応します。例えば、図3 の例では、「ドナ」を接頭辞に持つ区間は $[2,3]$ となります。この区間に含まれる接尾辞はすべて長さが $k$ 以上であること、一番最初の要素を除いて $\mathit{LCP}$ 配列の値は $k$ 以上 ($P$ を共通の接頭辞として持つため)であること、また、その区間の一番最初の要素の $\mathit{LCP}$ 配列の値は $k$ 未満 (一つ前の接尾辞は $P$ を接頭辞に持たないため)、であることが分かります。

以上のことから、$T$ 中の長さ $k$ の部分文字列の集合を $S_T(k)$ とすると、$|S_T(k)|$ 個の接尾辞については長さが $k$ 以上かつ対応する $\mathit{LCP}$ の値が $k$ 未満であること、$k-1$ 個の接尾辞についてはは長さが $k$ 未満かつ対応する $\mathit{LCP}$ の値が $k$ 未満であること、また、その他残りの接尾辞は対応する $\mathit{LCP}$ の値が $k$ 以上、ということになります。すなわち、値が $k$ 未満になる $\mathit{LCP}$ 配列の要素数が $|S_{T}(k)| + k -1$ となります。同様の議論で、値が $k+1$ 未満になる $\mathit{LCP}$ 配列の要素数は $|S_T(k+1)| + k$ となるため、値がちょうど $k$ となる $\mathit{LCP}$ 配列の要素数は $|S_T(k+1)| + k - (|S_T(k)| +k-1) = |S_T(k+1)| - |S_T(k)| + 1$ となります。次に、逆文字列 $T^R$ に対して同様の議論で、$T^R$の $\mathit{LCP}$ 配列の値がちょうど $k$ になる要素数は $|S_{T^R}(k+1)| - |S_{T^R}(k)|+1$ となります。

最後に、任意の $1 \leq k \leq n$ に対して長さ $k$ の部分文字列の種類数は逆文字列を考えても変わらないことから $|S_T(k)| = |S_{T^R}(k)|$ が成り立ち、それぞれの $\mathit{LCP}$ 配列の要素の多重集合は等しいことになります。(証明終わり)

つまり、これらのことから、以下が成り立ちます。

系
文字列 $T$ の LCP 配列と LPF 配列、文字列 $T^R$ の LCP 配列と LPF 配列はいずれもお互いの順列である。

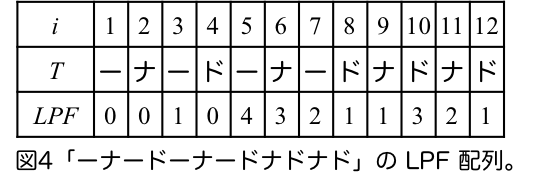
最後のダメ押しに、「ーナードーナードナドナド」の $\mathit{LPF}$ 配列を図4に示します。

確かに $\mathit{LPF}$ 配列は

$0$ が 3つ、$1$ が 4つ、$2$ が 2つ、$3$ が2つ、$4$ が1つ

となっています。なんというキモさでしょう！すごいですね。

まとめ

いかがでしたでしょうか。文字列を右から読んでも ($T^R$) 左から読んでも ($T$) 変わらないものとは $T$ と $T^R$ の $\mathit{LCP}$ 配列と $\mathit{LPF}$ 配列それぞれの全要素の多重集合でした。文字列マニア以外の方にはまったく面白くないと思いますが、文字列マニアでもまぁまぁ知らない人がいそうなので、話の種としての利用価値はあるかもしれません...

1. 「辞書式順序」の正確な定義は @nakashi18 さんの Lyndon 文字列入門 に書かれていますので、知らない人は参考にして見てください。 ↩

2. Toru Kasai, Gunho Lee, Hiroki Arimura, Setsuo Arikawa, Kunsoo Park: Linear-Time Longest-Common-Prefix Computation in Suffix Arrays and Its Applications, Proc. CPM 2001: 181-192. link ↩ ↩²

3. Enno Ohlebusch, Timo Beller, Mohamed I. Abouelhoda: Computing the Burrows–Wheeler transform of a string and its reverse in parallel, Journal of Discrete Algorithms 25 (2014) 21–33. link ↩