これは「文字列アルゴリズム Advent Calendar 2016」13日めの記事です。
この記事では有名な文字列圧縮法であるLZ77とLZ78、そしておまけとしてLZ78をシンプルに拡張したLZDについて簡単に紹介します1。
はじめに
LZ77とLZ78はそれぞれJacob ZivさんとAbraham Lempelさんが1977年と1978年に提案した可逆圧縮法です。可逆とは圧縮した文字列を元の文字列に復元可能なことを意味しています。LZ77はgzipやlz4、LZ78はgif画像の圧縮プログラムなどに使われており、提案されて40年弱立った今でも幅広い場面で使われる重要な圧縮法です。両者共シンプルな定義で、かつ様々な良い性質を兼ね備えていることから、単なる圧縮だけでなく圧縮索引やその他のデータ構造の計算などにも用いられています。
LZ77
LZ77分解
まずは、LZ77分解から説明します。
いきなり「分解」という言葉が出てきてびっくりしたかもしれません。実はLZ77は入力文字列を圧縮する圧縮法という側面と、入力文字列を分割する分解法という側面の2つを持っています(後ほど説明するLZ78とLZDも同様です)。本質を理解するためには、まずは分解法の側面に注目したほうがより理解が深まるので、まずは分解とは何か、そしてLZ77分解とは何かについて説明していきたいと思います。
文字列$T$が入力された時、$T=f_1, f_2, ..., f_n$を$T$の分解と定義します。各factor $f_i$は$T$の部分文字列を表し、$f_1$から$f_n$の連結文字列は$T$に一致します。より正確に述べると、$f_i$は$p_i=|f_1, ..., f_{i-1}|+1$から始まる$T$の部分文字列$T[p_i..p_i+|f_i|-1]$と一致します(ここで、文字列は1始まりで$p_1=1$とします)。
分解法では各factorをどのように定義するかが肝となります。LZ77分解ではfactor $f_i$を$p_i$未満に出現し最長一致する部分文字列とし、そのような部分文字列が出現しない場合は$T[p_i]$と定義します。
例を見ると分かりやすいです。
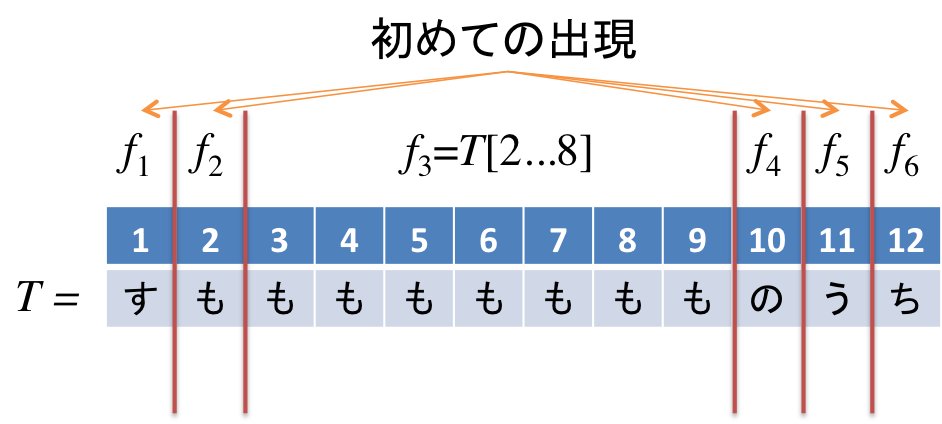
以下は、入力テキスト「すもももももももものうち(スモモも桃も桃のうち)」をLZ77分解した例です。
$f_1$、$f_2$は初めて出現する文字のため、1文字で分解されています。位置3から始まる$f_3$は3未満の位置2から始まる長さ7の部分文字列と最長一致します。$f_4$、$f_5$、$f_6$は初めて出現する文字のため、1文字で分解されています。
例から見て分かるように、各factorはそれ以前に出現した部分文字列で表され、繰り返しが多いような文字列は分割数が少なくなる傾向にあることが分かるかと思います。
LZ77の圧縮表現
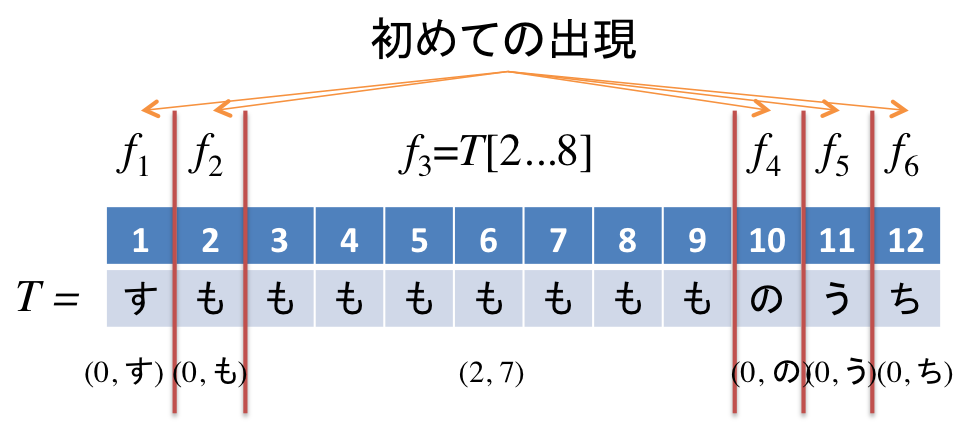
LZ77圧縮では各factorを文字列ではなく、2つの整数で表すことで圧縮を実現します。
factorが初めて出現した文字の場合は(0, その文字を表す整数)のペア、それ以外の場合は(一致した部分文字列の開始位置, その文字列の長さのペア)で表現します。
この圧縮表現の最大の特徴はfactorがどんなに長くても2つの整数で表せる点にあります。極端な場合、ababab...などの繰り返しは(0, a), (0, b), (1, 繰り返し回数)とどれだけ繰り返したとしても6つの整数で表すことが可能です。このように繰り返しが多い文字列の場合は分割数が少なくなり、結果として圧縮表現は入力文字列よりも小さくなる傾向にあります。
もちろんこの圧縮表現は元の文字列へ復元することが可能です。
先頭から順番にfactorを読み込んでいき、factorが始めて出現した文字を表す場合は整数で表された文字を、それ以外の場合はそれ以前の文字列を参照することで各factorが表す文字列を復元することが出来ます。
LZ78
LZ78分解
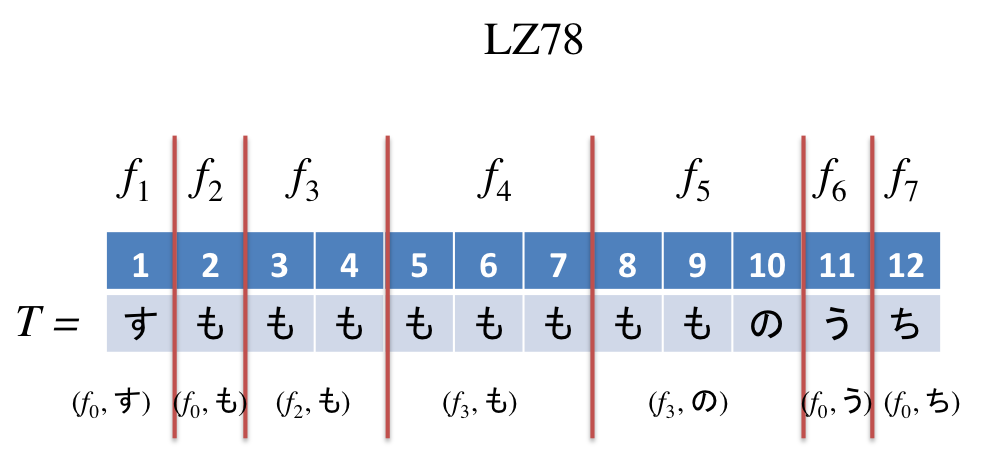
LZ78では文字列$T$が入力された時、$T=f_0, f_1, f_2, ..., f_n$に分解します。$f_0$は長さ0の空文字列を表します。LZ78の場合、$f_0$を導入したほうが定義がシンプルになるためこのように定義します。
さて、肝心のLZ78のfactorの定義です。
LZ78では、$f_0$以外のfactor $f_i$を$f_0$から$f_{i-1}$のfactorの中で最長一致するfactor $f_j$とそれに続く1文字$c$と定義します($f_i=f_j c$)。
LZ78はLZ77の最長一致する部分文字列の開始位置と終了位置に制限がついた分解法と考えるとわかりやすいでしょう。
LZ78の圧縮表現
LZ78では各factor $f_i=f_j c$は整数$j$と文字$c$のペアで表します(例ではわかりやすさのため、$f_j$のまま表示しています)。
LZ77と同様にそれ以前のfactor(と続く文字)で定義されているため、先頭から順に文字列を復元し参照することで元の文字列を復元することが出来ます。
LZ77とLZ78の比較
いろいろな観点から比較できますが、ここでは簡単に圧縮と、部分文字列展開の性能について比較したいともいます。
圧縮性能
LZ77とLZ78の圧縮性能を比べるとLZ77の方が優れています。これは両者とも、factorの開始位置未満の部分文字列で表されるという点は同じでありながら、LZ78には最長一致する部分文字列に制約があるためです。LZ77とLZ78で同じ位置から始まるfactorの長さを比較すると、LZ78のfactor長はLZ77のfactor長を超えることはなく、LZ77の分割数はLZ78の分割数を超えません。
部分文字列展開
あるfactorが表す文字列を得る部分文字列展開の操作はLZ78の方が優れています。LZ77は展開文字列の位置と長さで定義されるため、展開するためには対応する位置の部分文字列を参照する必要があり、この操作は最悪の場合、元の文字列全てを展開する必要があります。一方LZ78はfactorと文字のペアで定義されるため、展開するにはそのfactorを展開した文字列と文字を連結させるだけでよく、展開文字列長に比例した時間で展開することが出来ます。
小まとめ
まとめると、以下のようになります。
評価の程度は僕の主観を反映しています。
| 圧縮性能 | factorの展開 | |
|---|---|---|
| LZ77 | ◎ | ✕ |
| LZ78 | △ | ◎ |
LZD
最後はおまけとしてLZ78を拡張したLZ Double(LZD)を紹介します。
LZDではLZ78の定義を少しだけ変更するだけで、LZ78の利点であるfactorの展開の高速さを保ちながら、圧縮性能を向上させることが出来ます。
LZD分解
LZ78分解の分割数が多い(圧縮性能が低い)のはfactorの長さの増加が緩やかだということです。LZ77とLZ78は部分文字列をfactorに置き換えることで圧縮を実現してるため、当然ながらfactorが長くなればなるほど、置き換え可能な部分文字列が長くなり圧縮性能が良くなります。LZDではLZ78よりもfactorの長さの増加を加速させます。
それではLZDの定義に入りたいと思います。
LZ78の定義は$f_i=f_j c$のようにfactorと文字のペアでした($f_j$は最長一致する$f_0$から$f_{i-1}$のfactor、$c$は$f_j$に続く文字)。
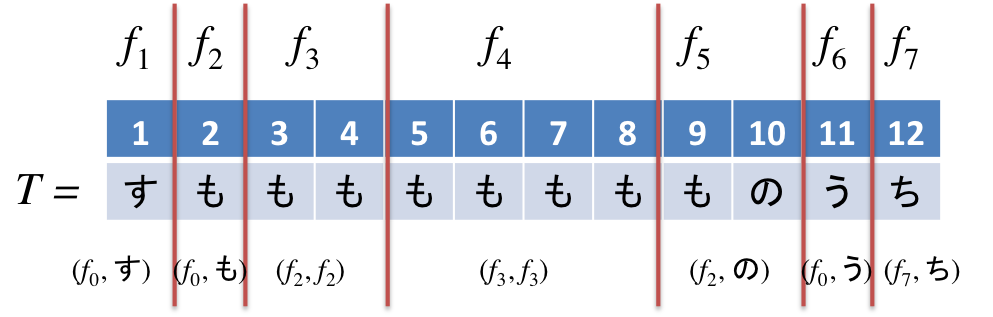
LZDでは$f_i=f_j f_k$のようにfactorとfactorのペア(double factor)となります($f_j$は最長一致する$f_0$から$f_{i-1}$のfactor、$f_k$は$f_1$から$f_{i-1}$のfactor、もしそのような$f_k$が無ければ$f_j$に続く1文字)。
え、これだけ?と思うかもしれませんが、はいこれだけです。
LZ78のfactorの長さの増加が緩やかな原因は1文字ずつしか増えない事が原因です。LZDでは最長一致するfactorの後に1文字追加するのではなく、そこからまた最長一致するfactorを追加することでこの問題を解決します。$f_j$と$f_k$で少し定義が違うのは、factorが必ず1以上になることを保証するというテクニカルな理由なのであまり気にしないでください
$f_4$の部分に着目すると、LZ78では3文字だった所がLZDでは4文字がになっており、LZDの方がfactorが長くなりやすく分割数も小さくなる傾向になることが分かるでしょう。
LZDの圧縮表現
LZ78とほとんど同じです。
最長一致するfactorを表す場合はその添字を、文字の場合は文字を表す数字で表し、各factorを2つの整数のペアで表します。
LZDとLZ77、LZ78の比較
圧縮性能
LZ78とLZDの理論的な圧縮性能の比較についてはまだ解析が十分ではありません。ただし実験的にはLZDの方がLZ78より分割数が小さくなることが確認されています。LZ77とLZDを比較した場合、LZ78と同様の観点から、LZ77の分割数はLZDの分割数を超えないことを示すことが出来ます。
部分文字列展開
LZDのfactorが表す文字列の計算はLZ78と同様で、展開文字列に比例した時間で求めることが出来ます。
小まとめ
まとめると以下のようになります。
| 圧縮性能 | factorの展開 | |
|---|---|---|
| LZ77 | ◎ | ✕ |
| LZ78 | △ | ◎ |
| LZD | ◯ | ◎ |
おわりに
簡単にですが、古典的でありながら現在でもよく使われている重要な圧縮法のLZ77とLZ78、そしてその拡張であるLZDを紹介しました。今回は計算方法について触れませんでしたが、興味のある方は是非調べてみて下さい。
参考文献
- Jacob Ziv, Abraham Lempel:
A universal algorithm for sequential data compression. IEEE Trans. Information Theory 23(3): 337-343 (1977) - Jacob Ziv, Abraham Lempel:
Compression of individual sequences via variable-rate coding. IEEE Trans. Information Theory 24(5): 530-536 (1978) - Keisuke Goto, Hideo Bannai, Shunsuke Inenaga, Masayuki Takeda:
LZD Factorization: Simple and Practical Online Grammar Compression with Variable-to-Fixed Encoding. CPM 2015: 219-230
-
LZ77は様々な亜種があります。この記事で紹介するLZ77は原著とは少し違いますが、現在のアルゴリズムの分野で最もよく使われている定義を取り扱います。 ↩