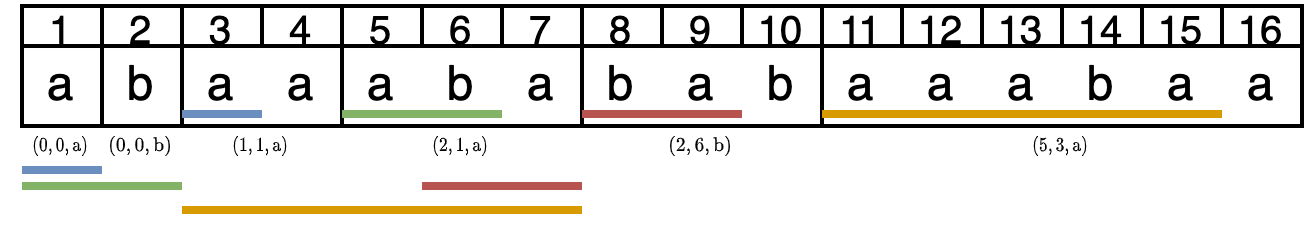どうも、文字列大好き @hdbn です。去年のアドベントカレンダーに予告がありつつも、エントリがなかったみたいなので LZ-End の話します。
LZ77 に代表される辞書式圧縮は、例えば Wikipedia や GitHub 等の編集履歴を含めた文書集合や、同一生物種のゲノムの集合など、極めて繰返しが多い様なデータ に対して有効であることから文字列業界では最近また注目されています。
LZ77 の基本的なアイディアは文字列中に複数回現れるような文字列の 2 回目以降の出現をそれ以前の出現への参照で表現することで圧縮する方法です。色々な変種がありますが、LZ77 では文字列を先頭(左)から見ていき、文字列を「『それ以前の出現を持つ最長の接頭辞』+ 1 文字」で項に分割していきます。このように分割をすると各項は、(以前の出現の長さ, 以前の出現の位置, 追加する 1 文字(の文字コード)) の整数三組で表現できます1 2。
LZ77 は線形時間で計算でき、高速に計算できる辞書式圧縮アルゴリズムの中では圧縮性能が理論的にも実用的にも最も良いものの1つとして知られていますが、圧縮率を損うことなく、(元のデータをすべて復元せずに)データの任意位置に効率よくアクセスする方法がまだ知られていません。この様な透過的なアクセスに適した辞書式圧縮としては、「LZ圧縮:LZ77とLZ78、そしてLZD」 で紹介されている LZ78 や LZD 等の「文法圧縮表現」がありますが、その圧縮性能は (仮に文字列を表現する最も小さい文法が求まったとしても) LZ77 と同等か、それ未満であることが知られています。
LZ-End はこのアクセスを効率良く行うことを目的に考案された LZ77 の変種で、文字列を分割する際の条件を「『終了位置が項の終わりに一致する様な、それ以前の出現を持つ最長の接頭辞』 + 1 文字」に変更したものです。以下に例を示します。
最初の 2 項は文字の初出現のため、以前の出現の長さ(空文字列)と出現の位置はそれぞれ 0 としています。第 3 項以降は以前の出現を色のついた横棒で示しています。以前の出現(下の枠外にある方の色のついた横棒)の終わりはすべて項の終わりに一致しています。特に、LZ77 との違いは第 4 項で初めて現れます。LZ77 では以前に $\mathrm{aba}$ までは出現しているので長さ 4 の項 $\mathrm{abab}$ となりますが、LZ-End では $\mathrm{aba}$ の以前の出現の終了位置 3 が項の終わりではないため採用できず、項の終わりの出現を持つ $\mathrm{ab}$ が採用され、1 文字追加した長さ 3 の $\mathrm{aba}$ が項となります。LZ-End の計算は LZ77 と比べると難しくなりますが、文字列の長さに線形な時間で求まることが知られています。
なお、図中では各項は (以前の出現の長さ, 以前の出現の位置, 追加する 1 文字) で表現していますが、(以前の出現の長さ, 終了位置が一致する項番号, 追加する 1 文字) と表現することもできます。上の例では $(0,0,\mathrm{a})$, $(0,0,\mathrm{b})$, $(1,1,\mathrm{a})$, $(2,2,\mathrm{a})$, $(2,4,\mathrm{b})$, $(5,4,\mathrm{a})$ となります。
このような表現にしておくと、任意の項の終了位置から左向きに 1 文字あたり定数時間で復元ができます。方法は簡単で、まずは目当ての項の三つ組にある「追加する 1 文字」が最後の文字であることがわかります。その後は、その項が参照している項番号の三つ組を見れば、その「追加する 1 文字」が最後から 2 番目の文字であることがわかります。後は同様に、再帰的に参照している項を辿っていきます。以前の出現が複数の項を跨っていたとしても、その前の項に対して同じことをします。
例えば、上の例で $(2,2,\mathrm{a})$ で表現される 4 番目の項の終了位置から展開してみましょう。
- まず、最後の文字は $\mathrm{a}$ です。残り 2 文字は項 2 の終わりと一致するので、次は項 2 を後ろから展開します。
- 項 2 は $(0,0,\mathrm{b})$ なので、次の文字は $\mathrm{b}$ であることがわかります。また、項 2 は長さが 1 文字なので、残り 1 文字は、その前の項 1 $(0,0,\mathrm{a})$ を後ろから展開します。
- 項 1 は $(0,0,\mathrm{a})$ なので、次の文字は $\mathrm{a}$ であることがわかります。
以上で 4 番目の項は $\mathrm{aba}$ であることがわかります。さらに左に展開したい場合は、3 番目の項で同様のことをします。
最近の話題
上で述べた方法では、任意の位置の 1 文字の復元が効率良くできることにはなりません。しかし、最近 $O(z_e)$ 領域 ($z_e$ は LZ-End の項数) のデータ構造で任意位置の文字を $\tilde{O}(1)$ 時間で復元する方法発見されました3。ちなみに、任意の文字列に対して $z \leq z_e$ が成り立ちます ($z$ は LZ77 の項数) が、$z_e$ が $z$ にくらべてどのくらい大きくなり得るかについてはまだ完全に分かっていません。具体的には $z_e = O(z\log^2 N)$ ($N$ は文字列の長さ) であることは証明されましたが、これがタイトかどうかは未解決です。
更に、項と以前の出現が重ならない、という条件を付した LZ77 (自己参照無し LZ77) の項数を $z_{\mathrm{no}}$ とすると、$z \leq z_{\mathrm{no}} \leq z_e$ が成り立ち、$z_e / z_{\mathrm{no}} = 2$ に近づく文字列の無限系列も知られていますが、$z_e/z_{\mathrm{no}} \leq 2$ と予想されています。つまり、LZ-End の項数は自己参照無し LZ77 の項数の定数倍しか悪くならないのではないか、といった予想です。
一方で、上で述べた LZ77/LZ-End の定義では、項の分割は左から貪欲に条件を満たす最長の項を採用していましたが、「最長の接頭辞」という条件を取り外し、全体で最も項数が小さくなるような分割するとどうでしょうか。LZ77 については貪欲が最適になりますが、LZ-End は分割する場所の選び方が以降の分割に影響するため、単純には解析ができません。最適 LZ-End は文法圧縮と比べると、同等か、より圧縮性能が良いことが知られています。しかし、最適 LZ-End を効率良く計算するのは簡単ではなさそうであり、また、貪欲 LZ-End と最適 LZ-End の項数の差がどの程度開き得るのかについてもまだ完全には分かっていません。
以上、まだ色々と細かい所が解明されていませんが、もしかすると圧縮性能とアクセスの高速性のより良いトレードオフを実現できる、魅力的な圧縮手法に今後なるのかもしれない LZ-End の紹介でした。来年には上で述べた幾つかの疑問が解決していると嬉しいですね!良いお年を!
参考文献
- Sebastian Kreft, Gonzalo Navarro: LZ77-Like Compression with Fast Random Access. DCC 2010: 239-248
- Sebastian Kreft, Gonzalo Navarro: On compressing and indexing repetitive sequences. Theoretical Computer Science 483: 115-133 (2013)
- Dominik Kempa, Dmitry Kosolobov: LZ-End Parsing in Linear Time. ESA 2017: 53:1-53:14
- Takumi Ideue, Takuya Mieno, Mitsuru Funakoshi, Yuto Nakashima, Shunsuke Inenaga, Masayuki Takeda: On the Approximation Ratio of LZ-End to LZ77. SPIRE 2021: 114-126
- Dominik Kempa, Barna Saha: An Upper Bound and Linear-Space Queries on the LZ-End Parsing. SODA 2022: 2847-2866
-
+1 文字を、以前の出現を持つ接頭辞がない(空文字列)の場合だけにする変種もあります。例えば 「LZ圧縮:LZ77とLZ78、そしてLZD」 の説明はそのバージョンです。 ↩
-
ここではビット表現まで符号化するまでの解析はせず、分解の項数を圧縮サイズと捉えることにします。 ↩
-
本当はそのアルゴリズムを紹介したかったのですが時間切れで LZ-End の簡単な紹介だけになってしまいました。機会があればまた... ↩