pytorchで初めてゼロから書くSOTA画像分類器（上）

#はじめまして

初投稿になります。よろしくお願いします。
これをやる前はゼロからネットワークを構築したことはありません。せいぜいGITHUB既存のコードをいじった程度です。
初めての挑戦ということで、タスクは一番簡単な画像分類で、CIFAR‐10データセットにしました。

この記事はタスクに対して、最低限動けるやつを、SOTAに近づけるように進化させていく過程を記録したものです。
対象はある程度理論を知っていて、実装経験があまりない方になります。
最終的にはGastaldi氏が2017年に発表したShake-Shake Regularizationを実装しています。
ライブラリはpytorchを使います。
pytorch tutorialやfastaiからいろいろ参考し、自己流に理解して書いたものになります。
これから初めての実装に踏み出そうとする人の参考になれればいいと思います。

初心者がやらかしそうな（実際やらかした）ことにも触れていきます。

#まずは最低限で動けるものを試しに作る
以下のことをやっていれば、画像分類器が完成します：

• データセットの準備
• data loaderの作成
• ネットワークを作る
• 損失関数, optimizerの指定
• training loopを書く

コードで一つずつ見ていきましょう。

###データセットの準備

TRAIN_PATH = './data/cifar/train/'
TEST_PATH = './data/cifar/test'
TRANSFORM = transforms.Compose([
    transforms.ToTensor(),
    ])
BATCH_SIZE = 32

train_data = torchvision.datasets.ImageFolder(root=TRAIN_PATH, transform=TRANSFORM)
test_data = torchvision.datasets.ImageFolder(root=TEST_PATH, transform=TRANSFORM)

パスとtransformの設定が必要です。
transformというのは実際の画像をどういう風に読み込むかのことです。
後述のnormalization, data augmentationもここでやります。
だが、今は何もやりません。ただ要求されたフォーマットに変えて、動けるようにします。

###data loaderの作成

train_loader = torch.utils.data.DataLoader(train_data, batch_size=BATCH_SIZE, shuffle=True, num_workers=4)
test_data = torchvision.datasets.ImageFolder(root=TEST_PATH, transform=TRANSFORM)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=BATCH_SIZE, shuffle=False, num_workers=4)

文字通り、どうやってデータをロードするかを設定するのがdata loaderです。
最低限training dataをシャッフルしましょう。
batch_sizeとnum_workerは主にメモリや演算速度に関連するものです。batch_sizeは他に収束とlearning rateに関係するが、この記事の主題ではないので説明を省けます。

###いよいよ本体を

class VeryBasicNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc = nn.Linear(3 * 32 * 32, 10)
    def forward(self, x):
        x = x.view(x.size(0), -1)
        x = self.fc(x)
        return x

これはディープですらないですが、試しにやってみます。パラメータ数は30,730。

###損失関数, optimizerの指定

nepoch = 4
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')

model = VeryBasicNet()
model.to(device)

loss_func = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)

分類タスクなので、損失関数をCross Entropyにします。
いろんなアーキテクチャを試す予定なので、便宜上optimizerは自動的に調節してくれるAdamにします。
Learning rateをとりあえず0.003に設定する以外、何もしません。

###training loopを書く

for epoch in range(nepoch):
    running_loss = 0.0
    for i, data in enumerate(train_loader):
        inputs, labels = data
        inputs = inputs.to(device)
        labels = labels.to(device)        
        optimizer.zero_grad()
        
        outputs = model(inputs)
        
        loss = loss_func(outputs, labels)
        loss.backward()
        
        optimizer.step()
        
        running_loss +=loss.item()
        
        if i%500 == 499:
            print("epoch:{}, step:{}, loss:{:.4f}".format(epoch+1, i+1, running_loss/500.))
            running_loss = 0.0
print("Finished training")        

correct = 0
total = 0

with torch.no_grad():
    test_loss = 0.0
    for data in test_loader:
        inputs, labels = data
        inputs = inputs.to(device)
        labels = labels.to(device)          
        outputs = model(inputs)

        loss = loss_func(outputs, labels)
        test_loss += loss.item()
        
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()
        
print("Accuracy on 10000 test image: %d %%" % (100 * correct / total))
print("Validation loss:{:.4f}".format(test_loss / (10000/BATCH_SIZE)))

これはtrainingを「epochの数」回まわして、最後に一度だけtestingをするように書いています。
これで最低限の画像分類器は完成しました。
さっそく結果を見てみましょう。

###結果

epoch:1, step:500, loss:2.3222
epoch:1, step:1000, loss:2.2138
epoch:1, step:1500, loss:2.1942
epoch:2, step:500, loss:2.1391
epoch:2, step:1000, loss:2.1111
epoch:2, step:1500, loss:2.1219
epoch:3, step:500, loss:2.1811
epoch:3, step:1000, loss:2.1709
epoch:3, step:1500, loss:2.1764
epoch:4, step:500, loss:2.0907
epoch:4, step:1000, loss:2.1205
epoch:4, step:1500, loss:2.0839
Finished training
Accuracy on 10000 test image: 32 %
Validation loss:2.1942

なんと、それなりに仕事をしてくれるではありませんか。
少なくともby chance の10%を上回っています。
だが、ここでは終わりません。
モデルを中心に、各部をレベルアップしていきます。

#Network部分のレベルアップ
###Deepにしてみる

class BasicNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(3 * 32 * 32, 40)
        self.fc2 = nn.Linear(40, 10)
    def forward(self, x):
        x = x.view(x.size(0), -1)
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return x

Accuracy on 10000 test image: 25 %
Validation loss:1.9429

パラメータ数123,330。
ロスは小さくなったけど、結果が悪くなっています。

###Conv layerを導入してみる

# just try some basic architectures
class BasicCNN(nn.Module):
    def __init__(self):
        super(BasicCNN, self).__init__()
        self.conv1 = nn.Conv2d(3, 8, 5)
        self.conv2 = nn.Conv2d(8, 16, 5)
        self.pool = nn.MaxPool2d(2,2)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)
        
    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

Accuracy on 10000 test image: 53 %
Validation loss:1.3162

パラメータ数62,958。
なんとこれだけで50%台に上りました。
便宜上チャネル数は適当にハードコードしたので、入念にいじったらもっと行けたかもしれません。
それでconvolution layerの威力が垣間見えます。

###Batch Normとdropoutを導入してみる

class BnLayer(nn.Module):
    def __init__(self, in_chan, out_chan, kernel_size=3, stride=2):
        super().__init__()
        self.dropout = nn.Dropout2d(p=0.2)
        self.conv = nn.Conv2d(in_chan, out_chan, kernel_size=kernel_size, stride=stride, padding=1, bias=False)
        self.bn = nn.BatchNorm2d(out_chan)
        
    def forward(self, x):
        return self.bn(F.relu(self.conv(x)))
    
class ConvBnNet(nn.Module):
    def __init__(self, layers, out_dim):
        super(ConvBnNet, self).__init__()
        self.conv1 = nn.Conv2d(3, layers[0], kernel_size=5, stride=1, padding=2)
        self.layer = nn.ModuleList([BnLayer(layers[i], layers[i+1]) for i in range(len(layers) - 1)])
        self.out = nn.Linear(layers[-1], out_dim)
        
    def forward(self, x):
        x = self.conv1(x)
        for l in self.layer: x = l(x)
        x = F.adaptive_avg_pool2d(x, 1)
        x = x.view(x.size(0), -1)
        return F.log_softmax(self.out(x), dim=-1)

layers = [10, 20, 40, 80]
out_dim = 10
model = ConvBnNet(layers, out_dim)

一見複雑になってきましたが、逐一見ていきます。

1. dropout層の導入。一言だとpの確率でユニットの値を0にして、過学習を防ぐ措置です。ここは軽めでp=0.2とします。これは簡単です。

2. BatchNorm2d層の導入。ここは論文自体を見ることお勧めします。
   例えば「猫と猫じゃない」の分類器を訓練するとします。
   仮に訓練に使うデータが黒猫しか含まれないとして、いざテストをするときにいろんな色の猫が出てきたら、分類がうまくできません。入力の分布が違いますから。その当たり前のことをCovariate Shiftと言います。
   ニューラルネットワークにも同じことが起きます。ある層nのパラメータの学習が前の層n-1の出力に基づきます。n-1層の出力の分布がゴロゴロ変わると、n層のパラメータの学習がうまくいきません。出力が変わるのが構いません、分布が変わるのがまずいのです。
   一層ならまだしも、多層ネットワークの場合になると伝言ゲームのように、影響が格段に大きくなります。
   それを解消すべく、層ごとの値をnonlinearity(e.g.ReLUなど)に入れる前に一度正規化します。それで前の層の出力の分布の変化を押さえます。
   しかし、正規化した値をそのまま使うとモデルの表現力を削ぐことになります。
   またそれを解消すべく、ユニットごとに新たに平均μと標準偏差σをパラメータとして与えます。それらパラメータは訓練可能(trainable)なので、それを使った「消して戻す」作業により、正規化したうえで、表現力を保つことができます（厳密な言い方ではありませんが、あくまでイメージとして）。そしてもう一つ、訓練中に得られた最終的なμとσ値ををテストの時に使うことになります。
   英語だが、Andrew Ng氏によるCovariate Shiftの解説がとても分かりやすいです。
   日本語の記事だとこの記事を参照すればいいでしょう。表現力のことについも書いてあります。

3. BatchNormの導入により、その前のConv2d層のbiasが不要になりました。bias=Falseにしています。別にあっても問題はありませんが、メモリがかかります。

4. 書き方として、ネットワークの部分を予めclassとして定義し(BnLayer)、後ほどネットワーク本体を書くときに呼び出すことができます。
   さらに、ネットワークを組む時にfor loopを使って同じ構造の層を複数作ることができます。
   先にnn.ModuleListを使って複数の層を一個のvariable(ここはself.layer)に丸め込みます。
   forwardの時にself.layerをfor loopで層ごと呼び出しています。
   print(model)するとこうなります。

ConvBnNet(
  (conv1): Conv2d(3, 10, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  (layer): ModuleList(
    (0): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(10, 20, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(20, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (1): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(20, 40, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(40, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (2): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(40, 80, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(80, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (out): Linear(in_features=80, out_features=10, bias=True)
)

パラメータ数39,650。
結果を見てみると、

epoch:4, step:1500, loss:0.9134
Finished training
Accuracy on 10000 test image: 13.320000 %
Validation loss:3.8425

ところが、ここで盛大に躓きました。
訓練ではロスが順調に下がっているのに、なぜテストではダメなんですか。
そう、ここで初心者やらかしたNo.1, model.eval()を忘れたからです。
テストに移行する前に、必ずmodel.eval()を入れましょう。
BatchNorm Layerは訓練とテストの時での動きが違いますので、BatchNormを入れるとテストのときにmodel.eval()にする必要があります。

上のコードのwith torch.no_grad():の前に、model.eval()を入れたら、無事解決：

epoch:4, step:1500, loss:0.9411
Finished training
Accuracy on 10000 test image: 65.820000 %
Validation loss:0.9660

いい感じに65%まで上がりました。

さらにディープにしてみます。

class DeepBnNet(nn.Module):
    def __init__(self, layers, c):
        super().__init__()
        self.conv1 = nn.Conv2d(3, 10, kernel_size=5, stride=1, padding=2)
        self.layers = nn.ModuleList([BnLayer(layers[i], layers[i+1]) for i in range(len(layers) - 1)])
        self.layers2 = nn.ModuleList([BnLayer(layers[i+1], layers[i+1], stride=1) 
                                      for i in range(len(layers) - 1)])
        self.out = nn.Linear(layers[-1], c)
        
    def forward(self, x):
        super(DeepBnNet).__init__()
        x = self.conv1(x)
        for l, l2 in zip(self.layers, self.layers2):
            x = l(x)
            x = l2(x)
        x = F.adaptive_max_pool2d(x, 1)
        x = x.view(x.size(0), -1)
        return F.log_softmax(self.out(x), dim=-1)

layers = [10, 20, 40, 80, 160]
out_dim = 10
model = DeepBnNet(layers, out_dim)

DeepBnNet(
  (conv1): Conv2d(3, 10, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  (layers): ModuleList(
    (0): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(10, 20, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(20, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (1): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(20, 40, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(40, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (2): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(40, 80, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(80, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (3): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(80, 160, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(160, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (layers2): ModuleList(
    (0): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(20, 20, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(20, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (1): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(40, 40, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(40, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (2): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(80, 80, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(80, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (3): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(160, 160, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(160, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (out): Linear(in_features=160, out_features=10, bias=True)
)

パラメータ数が一気に462,570まで跳ね上がりましたね。
ただ、この表記だと分かりにくいと思いますが、forwardのfor loopにより、実際のアーキテクチャが
self.layersの第0層＞self.layers2の第0層＞self.layersの第1層＞self.layers2の第1層＞....
のようになっているはずです。

Accuracy on 10000 test image: 71.060000 %
Validation loss:0.8312

70%台まで上がりました。
まだまだ行けます。

#ResNetを導入してみる

class BnLayer(nn.Module):
    def __init__(self, in_chan, out_chan, kernel_size=3, stride=2):
        super().__init__()
        self.dropout = nn.Dropout2d(p=0.2)
        self.conv = nn.Conv2d(in_chan, out_chan, kernel_size=kernel_size, stride=stride, padding=1, bias=False)
        self.bn = nn.BatchNorm2d(out_chan)
        
    def forward(self, x):
        return self.bn(F.relu(self.conv(x)))

class ResnetLayer(BnLayer):
    def forward(self, x): return x + super().forward(x)

class Resnet(nn.Module):
    def __init__(self, layers, c):
        super().__init__()
        self.conv1 = nn.Conv2d(3, 16, kernel_size=5, stride=1 ,padding=2)
        self.layers = nn.ModuleList([BnLayer(layers[i], layers[i+1]) for i in range(len(layers) -1)])
        self.layers2 = nn.ModuleList([ResnetLayer(layers[i+1], layers[i+1], stride=1)
                                     for i in range(len(layers) -1)])
        self.layers3 = nn.ModuleList([ResnetLayer(layers[i+1], layers[i+1], stride=1)
                                     for i in range(len(layers) -1)])
        self.out = nn.Linear(layers[-1], c)
        
    def forward(self, x):
        x = self.conv1(x)
        for l, l2, l3 in zip(self.layers, self.layers2, self.layers3):
            x = l3(l2(l(x)))
        x = F.adaptive_max_pool2d(x, 1)
        x = x.view(x.size(0), -1)
        return F.log_softmax(self.out(x) ,dim=-1)

layers = [16, 32, 64, 128, 256]
out_dim = 10
model = Resnet(layers, out_dim)

BnLayerは上からを流用します。
ResnetLayerの方はまずBnLayerクラスのメソッドを継承します。それからインプットのxを二つに分かれて（1.そのまま, 2.継承先(BnLayer)のforwardを経由したもの。）、加算します。(fastaiの例でもこの書き方のはず)

ResNetとは要するに入力と出力のマッピングより、入力と出力の差分（残差）を用いてパラメータの学習をしようとするものです。
イメージとしてはこうなります。
---->
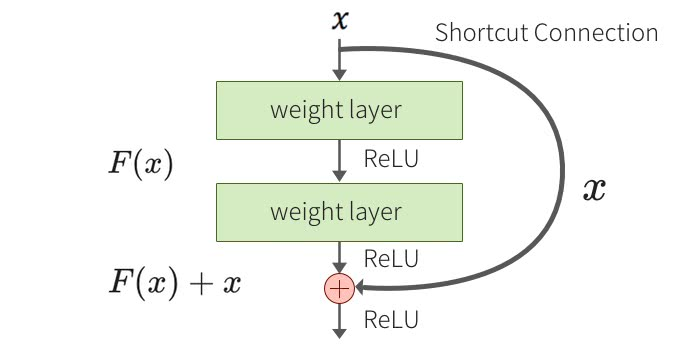
これにより従来の十数層のネットワークより遥かに深く、百層以上のネットワークを構築することを可能にしています。
ResNetについては詳しく説明してくれる記事が山ほどあるので、ここでは割愛します。

アーキテクチャを見てみると

Resnet(
  (conv1): Conv2d(3, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
  (layers): ModuleList(
    (0): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(16, 32, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (1): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(32, 64, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (2): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (3): BnLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (layers2): ModuleList(
    (0): ResnetLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (1): ResnetLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (2): ResnetLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (3): ResnetLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (layers3): ModuleList(
    (0): ResnetLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (1): ResnetLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (2): ResnetLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (3): ResnetLayer(
      (dropout): Dropout2d(p=0.2)
      (conv): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (out): Linear(in_features=256, out_features=10, bias=True)
)

上と同じ、forwardのfor loopにより、実際のアーキテクチャが
self.layersの第0層＞self.layers2の第0層＞self.layers3の第0層＞self.layersの第0層＞....
すなわちBatchNorm(16, 32)>Resnet(32, 32)>Resnet(32, 32)>BatchNorm(32, 64)>....
のようになっているはずです。

ただ、このモデルだと、パラメータ数が1,965,066になりました。

結果については

Accuracy on 10000 test image: 73.280000 %
Validation loss:0.7926

よくはなりましたが、あんまり伸びなかったですね。

#最後に
結構長くなりましたので、前後編に分けようと思います。
後編ではこの記事の肝となるShake-Shake Regularizationの実装について書きます。
pytorchで初めてゼロから書くSOTA画像分類器（下）(Shake-Shake Regularization実装)