前提
本記事では、.csはUnityC#を表し、.shaderはshaderlabsを表すことを前提とします。
また、前回の記事で三角関数を理解しているものとします。
概要
今回、ベクトルを0から説明すると膨大なので、この記事を読む人の経験に合わせた記事構成にしています。
あなたの読みたいと思ったところから読むといいと思います。
ただ、ベクトルの概念は初めて読むと理解しづらい部分もありますので、ゆっくり考えてみてください。
数学的基礎
ベクトルとは
ベクトルのとは、向きと大きさを持つものです。
これの反対としてスカラーがあり、これは大きさのみを持つものです。
例として、遠心力は向きと大きさを持つのでベクトル量ですが、体重は大きさのみを持つのでスカラー量です。
単純に、「0」とか「$\pi$」とかもスカラー量です。
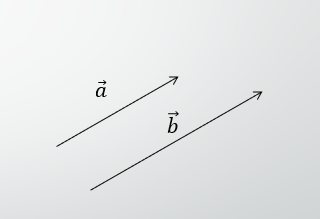
またベクトルは、向きと大きさを持つので、必ず始点と終点が存在します。
矢印を書くと、必ず始点と終点が存在するはずです。
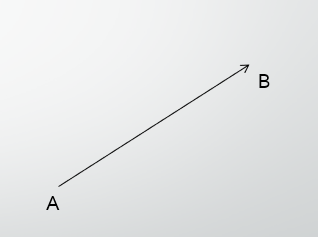
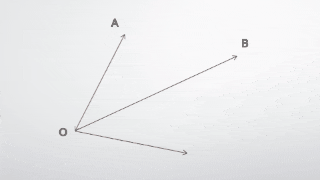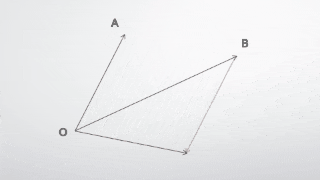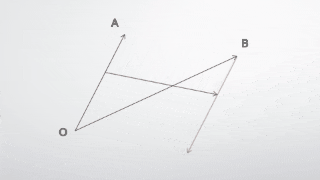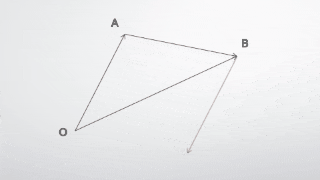
下図の矢印は、点Aから点Bに矢印が書かれているので $\overrightarrow{AB}$ と書きます。
くれぐれもABの書き順を逆にしないように!!
もし、 $\overrightarrow{BA}$ と書くと、逆ベクトルとして点Bから点Aに矢印が書かれます。
なのでこの関係から、このように書くこともできます。
\vec{BA}=-\vec{AB}
ベクトルの和算・減算
ベクトルは、スカラーのように和と差を求めることができますが、少し扱いがトリッキーです。
まずは和について考えていきましょう。
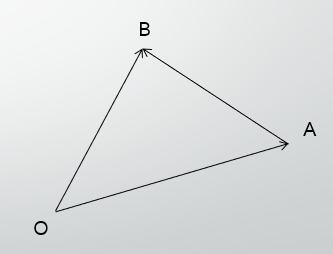
下図のように、三点$O,A,B$があるとしましょう。
すると、 $\overrightarrow{OB}$ は次のように表せます。
\vec{OB}=\vec{OA}+\vec{AB}
これがなんとなく直感的にわかるといいですね。
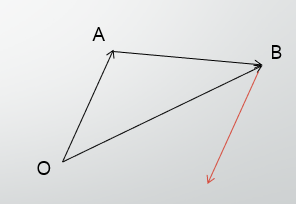
これと同様にして、減算も考えていきます。
減算はベクトルからベクトルを引くという考え方ではなく、ベクトルと逆ベクトルを足すという考え方をします。
なので、減算は以下の通りになりますが、仕組みとしては下図のとおりです。
\vec{AB}=\vec{OB}-\vec{OA}=\vec{OB}+(-\vec{OA})
減算の仕組みは毎度悩みますが、悩むたびに図を描くといいでしょう。
ベクトルのスカラー倍
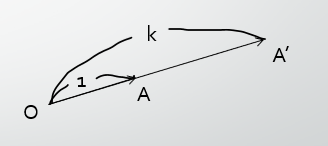
そもそもスカラー倍とは、$\times2$とか$\times\pi$のように、何倍の「何」の部分がスカラーである倍率のことを言います。
なのでベクトルのスカラー倍とは、$k$を実数として、 $k\overrightarrow{OA}$ のようなものです。
スカラー倍の応用
ある二つのベクトル $\vec{a},\vec{b}$ が平行にあるとします。
このとき、ベクトルは位置を考えないため次のことが言えます。1
\vec{a} // \vec{b}⇔\vec{b}=k\vec{a}~~~~~~(ただし、kは実数)
これをベクトルの平行条件と言います。
また、この条件は一直線上にあるための条件ともなります。
ベクトルの積
ベクトルの積はかなり気を使ってください。なぜなら積が複数存在するからです。
内積
まずは、内積について説明します。
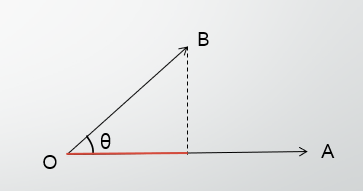
内積は、二次元以上の世界で発揮するスカラー量です。
内積の定義は以下の通りです。2
(内積を表すときは「$\times$」は禁止です。かならず「$\cdot$」を使います。)
\vec{a} \cdot \vec{b}=|a||b|\cos{θ}~~~~~~(0\leqθ\leq\pi)
。。。
なにこれ。って感じですよね。
実際なんでこういう定義なのか。
上図を例に挙げると、上に太陽があった時、ベクトルOAの赤い部分はベクトルOBの陰になりますよね。
その陰になる部分の長さが内積によって求まります。
じゃあいったい何に使うのかっていうのが次の話です。
ちなみに、ベクトルを成分表示すると次のように内積を表すこともできます。
\vec{a}=(a_1,a_2),\vec{b}=(b_1,b_2)とすると
\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2
内積の応用
先ほどは、ベクトルの平行条件について紹介しました。
実は、内積を用いることで垂直条件を作れます。
実際に見ていきましょう。
ある二つのベクトルが垂直にあるとします。
このときの内積を求めてみると
\vec{a} \cdot \vec{b}=|a||b|\cos\biggl({\frac{\pi}{2}}\biggr)=0
となります。($\cos$が垂直だと0をとるため)
なので、垂直条件は次の通りとなるわけです。3
\vec{a}\perp\vec{b} ⇔ \vec{a}\cdot\vec{b}=0
また、実際にCG(例えばlight方向ベクトルの計算とか)で内積を使いますが、ベクトルの長さを考える必要が無い時、$|a|=|b|=1$とすることがあります。
なので、こうしたときの内積は次のようにあらわされるため、内積は実質$\cos$ということになるわけです。
\vec{a} \cdot \vec{b}=1\times1\times\cos{θ}=\cos{θ}
外積
もう一つの積は、外積と呼ばれるものです。
外積は一次元・三次元・七次元の世界でのみ発揮されるベクトル量です。
こちらの演算子は「$\times$」で表します。「$\cdot$」は禁止です。
厳格ではないですが、三次元空間での定義は以下の通りです。
\vec{a}=(a_1,a_2,a_3),~\vec{b}=(b_1,b_2,b_3)とすると、
\vec{a} \times\vec{b}=(a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_1b_2-a_2b_1)
。。。なんでこんな複雑な式なんだ。
という顔をしていますね。
理由については、行列を話すときに教えましょう。
今はこういうものなのかを唇を噛みしめてください。
では、外積にどんな利点があるのかを見ていきましょう。
外積の応用
先ほどの定義の時にも話しましたが、外積はベクトルを表します。
実際、$x$成分、$y$成分、$z$成分がありますからね。
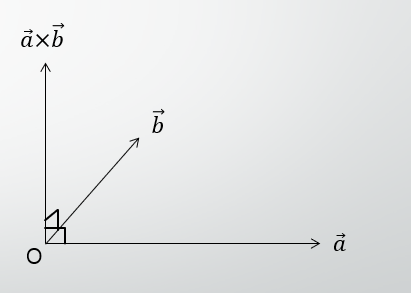
では、 $\overrightarrow{a}\times\overrightarrow{b}$ は一体どんなベクトルでしょうか。
実は、 $\overrightarrow{a}$とも $\overrightarrow{b}$ とも垂直なベクトル成分を表します。
下図のような感じですね。
なので、外積ベクトルは主に、ポリゴンの法線4ベクトルとかに使用されるケースが多いかと思います。
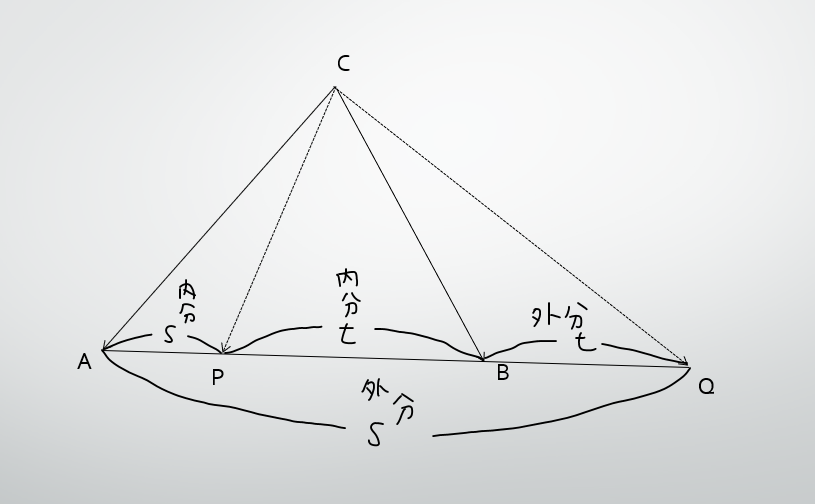
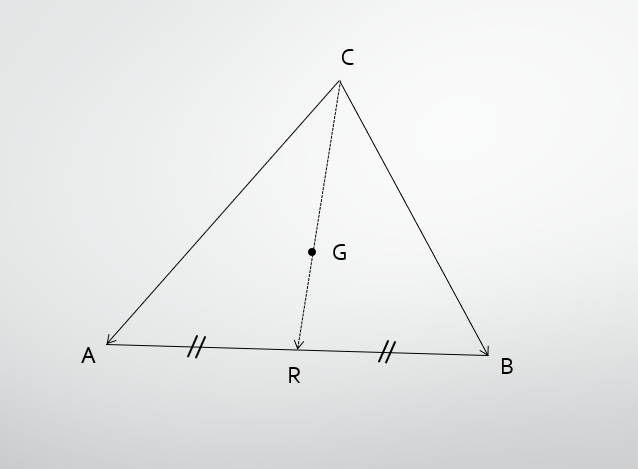
内分・外分・重心
そもそも内分外分って何?とか位置ベクトル5とは?ってなったらこことかを参照しながら見てください。
二つのベクトル $\overrightarrow{a},\overrightarrow{b}$ が張る三角形ABCのある線分を「$s:t$」に内分・外分する内分点、外分点と中点、重心を表す位置ベクトルをそれそれ$P(\overrightarrow{p})$、$Q(\overrightarrow{q})$、$R(\overrightarrow{r})$、$G(\overrightarrow{g})$とするとき、
\vec{p}=\frac{t\vec{a}+s\vec{b}}{s+t}
\vec{q}=\frac{-t\vec{a}+s\vec{b}}{s-t}
\vec{r}=\frac{\vec{a}+\vec{b}}{2}
\vec{g}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}
ベクトル方程式
ベクトルで表された方程式をベクトル方程式といいます。
2次元
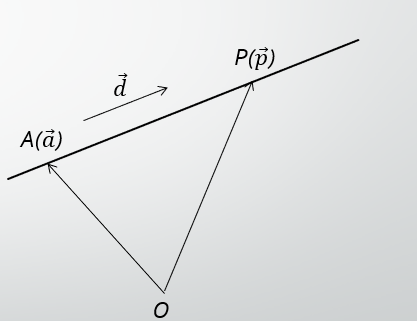
直線のベクトル方程式
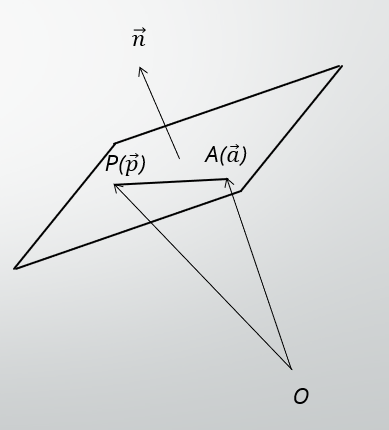
上図のような状態を考えると、直線上の任意の位置ベクトル$P(\overrightarrow{p})$は以下のように表されます。
\vec{p}=\vec{a}+t\vec{d}~~~~~(tは実数)
ここで、 $\overrightarrow{d}$ のことを方向ベクトルといい、点Aから点Pへの方向を表します。なので、 $\overrightarrow{d}$ の長さは1で良いのです。
$t$はAP間の距離を表すので、任意の実数です。
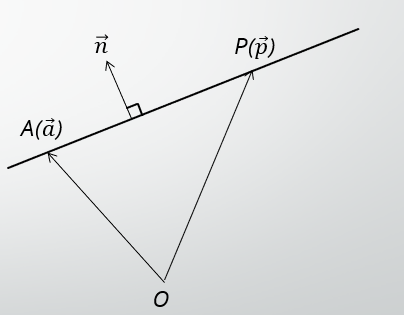
また、上図のような状態を考えることもできます。
すると、直線のベクトル方程式は次のように内積で表せるのです。
\vec{n}\cdot\overrightarrow{AP}=0
このとき、 $\overrightarrow{n}$を法線ベクトルと言います。 同じように長さの情報は必要ないので、$|\vec{n}|=1$で良いのです。
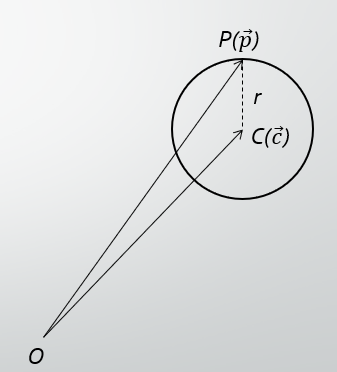
円の方程式
上図のような状態を考えると、円上の任意の位置ベクトル $P(\overrightarrow{p})$ は次のように表されます。6
|\vec{p}-\vec{c}|=r~~~~~(r>0)
(\vec{p}-\vec{c})(\vec{p}-\vec{c})=r^2
$\overrightarrow{c}$ は円の中心を表し、$r$は円の半径を表します。
3次元
平面の方程式
上図のような状態のとき、平面上の任意の点をPとすると、平面のベクトル方程式は次のように表せます。
\vec{AP} \cdot \vec{n} =0
ここで、$\vec{n}=(a, b, c)、A=(x_0, y_0, z_0)、P=(x, y, z)$とすると、原点をOとして、
\vec{AP}=\vec{OP}-\vec{OA}=(x-x_0, y-y_0, z-z_0)
となるので、これをベクトル方程式に当てはめると、
\vec{AP} \cdot \vec{n}=a(x-x_0)+b(y-y_0)+c(z-z_0)=0
ax+by+cz-(ax_0+by_0+cz_0)=0
$d=-(ax_0+by_0+cz_0)$と置くことで、平面の方程式は
ax+by+cz+d=0
となります。
球の方程式
球の方程式を考えるとしても、ベクトル方程式ならば二次元の時と全く同じ式になるので、
|\vec{p}-\vec{c}|=r~~~~~(r>0)
となります。よって
$P=(x,y,z)、C=(x_0,y_0,z_0)$とおくと。
(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=r^2
という成分表示になります。
実践
ここからは、実際にベクトルはどのように活用されているかの一例を取り上げます。
著者の傾向もあると思います。
内積の使用例
内積の使用例として、平行光源のオブジェクトに対する拡散光の計算に使用されたりします。
例としては、以下の通りです。
fixed4 frag(v2f i) : SV_Target
{
fixed4 col = tex2D(_MainTex, i.uv);
float3 lightDirection = normalize(_WorldSpaceLightPos0.xyz);
float3 normal = normalize(i.normal);
//ここで内積を用いて拡散度合いを計算している
//max関数を用いているのは、負数を発生させないため。
float diffuse = max(dot(lightDirection, normal), 0.0);
return diffuse * col;
}
外積の使用例
カメラを操作する場合とかに外積が使用されることもあります。
極端ではありますが、例を挙げてみましょう。
二つのベクトル$v_1,v_2$がわかっているとします。
その二つを用いてどちらにも垂直なベクトルを求めようとすると、以下の通りです。
Vector3 CulcVector(Vector3 a, Vector3 b)
{
return Vector3.Cross(a, b);
}
Vector3 v1 = new Vector3(1.0f, 0.0f, 0.0f);
Vector3 v2 = new Vector3(0.0f, 1.0f, 0.0f);
//外積で第三のベクトルを求めている
Vector3 v3 = CulcVector(v1, v2);
//この計算ではv3は(0.0f, 0.0f, 1.0f)のベクトルになる
内分の使用例
内分の計算自体はUnityで事前に用意されており、Lerpという関数があります。
なので、それを使って内分計算することが可能です。
例では、$v_1, v_2$のちょうど中点を求めています。
Vector3 v1 = new Vector3(2.4f, 5.2f, 8.4f);
Vector3 v2 = new Vector3(1.5f, 3.5f, 0.2f);
//中点を求めている
Vector3 vp = Vector3.Lerp(v1, v2, 0.5f);
ベクトル方程式の使用例
ベクトル方程式、レイマーチングのレイを飛ばすときなんかに使いますよねー(かなりニッチ)
fixed4 frag(v2f i) : SV_Target
{
float3 ro = i.camerapos;
float3 rd = normalize(i.pos - i.camerapos);
float ds = 0;
fixed3 col = 0;
for (int i = 0; i < 99; i++)
{
//ここで直線のベクトル方程式のようなものを使っている!!
float3 pos = ro + rd * ds;
float d = length(pos) - 2.0;
if (d < 0.0001)
{
col = float3(1.0 - (float)i*0.02, 1.0 - (float)i*0.02, 1.0 - (float)i*0.02);
break;
}
ds += d;
}
return fixed4(col, 1);
}
以上で、ベクトルに関する基本的なものを紹介しました。
誤字等ありましたら、リクエストお願いします。
次回は行列に関する話が出来たらなと思っています。