前提
本記事では、.csはUnityC#を表し、.shaderはshaderlabsを表すことを前提とします。
話題に入る前に
弧度法
通常、私たちは角度を表すときに 180° のように度数法で表すことが多いですが、三角関数ではこれとは別に弧度法で角度を表現するのが一般的です。
本記事でも弧度法を普通に扱っていくので、内容に入る前に紹介していこうと思います。
視点としては、一周をどのように定義しているだろうか?という部分に着目していきます。
度数法では、一周を$360°$として角度を表現し、単位に「°」を用います。
反対に弧度法は、一周を$2\pi$として角度を表現し、単位に「ラジアン」を用いる表現方法です。1
なので関係式としては、同じ一周という部分に着目しているので、
2\piラジアン=360°⇔1°=\frac{\pi}{180ラジアン}
という関係式が導けます。
なので、もし本記事を読んでいて弧度法で何度か分からない時は最後の式を活用してもらえればと思います。
例えば、$30°$は何ラジアンなのかを計算するとこのようになります。
\frac{\pi}{180}×30=\frac{\pi}{6}
ちなみに、コードで表すと次のようになります。
float angle = 30f; //度数表示
float rad; //弧度法
rad = angle * Mathf.Deg2Rad; //弧度変換
三角関数の定義
三角関数自体は次のように定義されていますが、CG屋には必要ないため興味ある人だけ見るといいと思います。
**正式な定義**
-
>
- *define*(三角関数) >
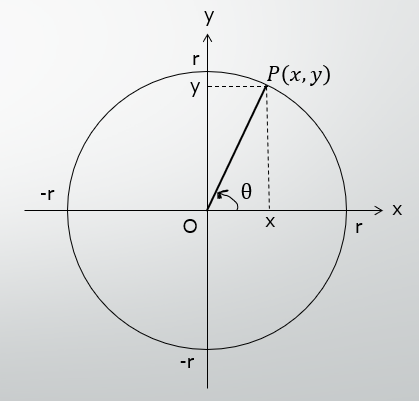
- 座標平面上で、下図のように$x$軸の正の部分に始線をとり、一般角$\theta$の動径と原点を中心とする半径$r$の円との交点$P$の座標を$(x, y)$とする。(下図参照)
この時、$\frac{y}{r}, \frac{x}{r},\frac{y}{x}$の各値は円の半径$r$に関係なく$\theta$だけで定まるので、$\sin\theta, \cos\theta, \tan\theta$を
\sin\theta=\dfrac{y}{r}, \cos\theta=\dfrac{x}{r}, \tan\theta=\dfrac{y}{x}
>と定め、それぞれ一般角$theta$の、**正弦、余弦、正接**と言う。 これらはどれも$\theta$の関数であり、まとめて**三角関数**という。 (もういちど読む数研の高校数学 より) </dd> </dl> </div></details> *** 定義自体は長いですが、簡潔にまとめると以下のようになります。 ```math \sin\theta=\dfrac{y}{r}, \cos\theta=\dfrac{x}{r}, \tan\theta=\dfrac{y}{x}これをまとめて三角関数と呼びます。($x,y,r,\theta$は下図や定義内参照)
三角関数自体の定義はこうなっていますが、CGの世界では$r=1$で扱うことが非常に多いです。
(なぜなら、角度の度合いしか考えないため、長さは必要ないと考えることが多いから)
なので、$r=1$とすると、定義はこのように変えれます。\sin\theta=y, \cos\theta=x, \tan\theta=\dfrac{y}{x}こうすると凄いシンプルに考えれますね。
(補足)
感の良い人なら分かると思いますが、$\tan\theta$は直線の傾きを表します。
この性質は、CG屋でよく使う話なので覚えておくと良いでしょう。
上図を例にして、原点と点Pの傾きを考えてみます。*** # 三角関数の値の求め方 基本的に、三角関数の値は計算機を使わない限りほとんどわからないです。 しかし、有名角[^2]のみは知られている($\tan\frac{\pi}{2}$を除く)のでそれを紹介します。 そして、以降は弧度法で角度を書きます。 *****例**
-
直線の傾きは
(直線の傾き)=\dfrac{(yの変化量)}{(xの変化量)}なので、上図の直線OPの傾きは
(直線の傾き)=\dfrac{(y-0)}{(x-0)}=\dfrac{y}{x}となりますが、これは$\tan\theta$と同じ値ですね。
なので、ここからも$\tan\theta$は直線の傾きを示すことがわかると思います。角度 $\sin\theta$ $\cos\theta$ $\tan\theta$ $0$ $0$ $1$ $0$ $\dfrac{\pi}{6}$ $\dfrac{1}{2}$ $\dfrac{\sqrt{3}}{2}$ $\dfrac{1}{\sqrt{3}}$ $\dfrac{\pi}{4}$ $\dfrac{1}{\sqrt{2}}$ $\dfrac{1}{\sqrt{2}}$ $1$ $\dfrac{\pi}{3}$ $\dfrac{\sqrt{3}}{2}$ $\dfrac{1}{2}$ $\sqrt{3}$ $\dfrac{\pi}{2}$ $1$ $0$ undefined $\pi$ $0$ $-1$ $0$ $2\pi$ $0$ $1$ $0$
このように有名角は値が知られているので、それを組み合わせてあらゆる角度に対する値を計算します。
しかし、どのように計算するのか。
三角関数にはこれらを解決するための公式がたくさんあります。
三角関数の様々な公式
ここからは、こんな公式があるというのを紹介していくので、こんな公式があるんだ程度に見てください。
また、実際に角度変換する際としての参照先として使ってくれるとありがたいです。
三角関数の相互関係
$\sin\theta,\cos\theta,\tan\theta$には次のような関係があります。
\tan\theta=\frac{\sin\theta}{\cos\theta}\sin^2\theta+\cos^2\theta=11+\tan^2\theta=\dfrac{1}{\cos^2\theta}特に、$\sin^2\theta+\cos^2\theta=1$は非常によく使うので、覚えておくと良いでしょう。
少し解説すると、一番目は、$\tan\theta$の定義であり、二番目は定義の図の斜辺の求め方であり、三番目は二番目の式の両辺を$\cos^2\theta$で割ると出てきます。
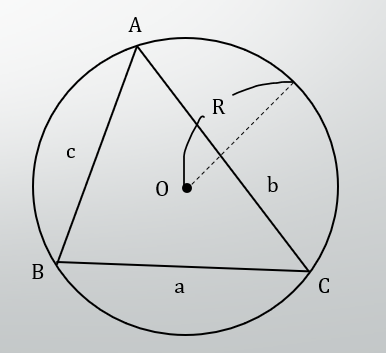
正弦定理
下図のように三角形ABCがあり、三角形の外で接する外接円の半径をRとすると、以下のような関係が成り立ちます。
\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}=2Rこの定理は外接円とも絡むため、CG屋としての出番はそんなにないかもしれないです。
角度同士の関係を導く際には使うかもしれません。
ちなみにこれをコードにすると以下の通りとなります。
example1.csa / Mathf.Sin(A) == 2 * R; //正弦定理example1.shadera / sin(A) == 2 * R //正弦定理example2.csb / Math.Sin(B) == c / Mathf.Sin(C); //正弦定理example2.shaderb / sin(B) == c / sin(C); //正弦定理
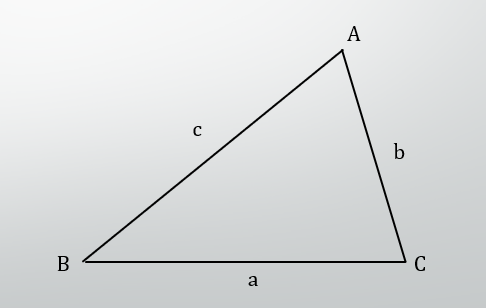
余弦定理
下図のような三角形ABCにおいて、以下のような関係が成り立ちます。
a^2=b^2+c^2-2bc\cos{A}b^2=c^2+a^2-2ca\cos{B}c^2=a^2+b^2-2ab\cos{C}こっちのほうがかなりCG屋としても使うことが多いでしょう。
(辺の長さを求めるのに便利なため)
ちなみに余弦定理をコードで書くと次のようになります。
example.csa * a == b * b + c * c -2 * b * c * Mathf.Cos(θ); //余弦定理example.shadera * a == b * b + c * c -2 * b * c * cos(θ); //余弦定理
加法定理
三角関数を扱う上で以下の式は非常に重要な式となっています。
コード上では、任意の角度でコンピュータが計算してくれるので必要ないですが、論理を考える際には切っても切れない関係式です。\sin(α+β)=\sinα\cosβ+\cosα\sinβ\sin(α-β)=\sinα\cosβ-\cosα\sinβ\cos(α+β)=\cosα\cosβ-\sinα\sinβ\cos(α-β)=\cosα\cosβ+\sinα\sinβと言っても、覚えておくのは一番目と三番目だけで十分ですよ。
(他は符号を変えるだけなため)
倍角の公式・半角の公式
倍角の公式は加法定理を変形して作ります。
(具体的には、$α$と$β$を共に$\theta$とする。)
コード上では、任意の角度でコンピュータが計算してくれるので必要ないですが、同じく論理を考える際に出てくるでしょうね。
結果としては以下の通りです。\sin2\theta=2\sin\theta\cos\theta\cos2\theta=\cos^2\theta-\sin^2\theta=2\cos^2\theta-1=1-2\sin^2\theta一方で、半角の公式は倍角の公式を移項して作ります。
結果としては、以下の通りです。\sin^2\theta=\dfrac{1-\cos2\theta}{2}\cos^2\theta=\dfrac{1+\cos2\theta}{2}
和積の公式
和積の公式も、加法定理を四則演算して作られます。
この公式、意外と便利なので論理を考える際に使うこともしばしば。
和積の公式は以下の通りです。\sinα+\sinβ=2\sin\frac{α+β}{2}\cos\frac{α-β}{2}\sinα-\sinβ=2\cos\frac{α+β}{2}\sin\frac{α-β}{2}\cosα+\cosβ=2\cos\frac{α+β}{2}\cos\frac{α-β}{2}\cosα-\cosβ=-2\sin\frac{α+β}{2}\sin\frac{α-β}{2}
ここまで理解しておけば、三角関数分野としては申し分ないはずです。
きっと、どのコードを見ても三角関数部分は基礎で詰まることはないでしょう。
おまけ
三角関数を実際どのように応用するかについていくつか紹介します。
逆三角関数
逆三角関数とは、三角関数の逆関数の総称のことを言います。
逆関数については、このサイトが良いでしょう。
実際に、簡易的な定義としては以下の通りです。y=\arcsin{x}=\sin^{-1}{x} ⇔ x=\sin{y}y=\arccos{x}=\cos^{-1}{x} ⇔ x=\cos{y}y=\arctan{x}=\tan^{-1}{x} ⇔ x=\tan{y}UnityC#だと、ASin, Acos, Atan, Atan2であり、shaderlabsだとasin, acos, atan, atan2という組み込み関数が逆三角関数にあたります。
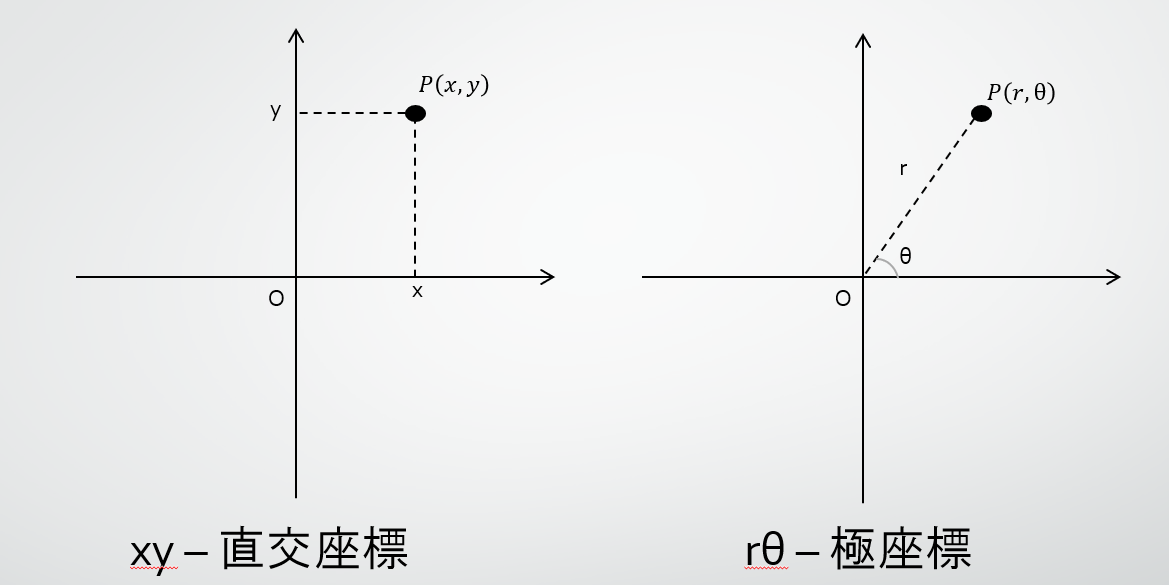
極座標変換
極座標変換とは、x軸とy軸が直交する直交座標系を角度と長さで表す極座標系に変換すること言います。
極座標の良い所として、曲線的な動きが得意という強みがあるのでたびたび使われます。
では、実際に数学的に見てみましょう。
直交座標系での点Pの座標を(x,y)とし、同地点に対応する極座標系の座標を(r,$\theta$)とします。
このとき、x,yとr,$\theta$の関係は以下の通りとなります。r=\sqrt{x^2+y^2}θ=\tan^{-1}{\frac{y}{x}}これの応用例として、uvの極座標変換があるので、コードを載せておきます。
example.shaderfloat dividePI = 1 / (3.14159265358 * 2); //正規化のための1/π^2 float uv = 2* i.uv - 1; // uv定義域を[0, 1]から単位円の[-1, 1]へ float r = 1 - sqrt(uv.x * uv.x + uv.y * uv.y); //極座標の長さの定義 float theta = atan2(uv.y, uv.x) * dividePI; //極座標の角度の定義。 uv.x = theta; uv.y = r;
さらに気になる方はこの記事を読んで見ると良いでしょう。
本質的な部分が多いので、理解すると非常に面白いと思います。
https://qiita.com/drken/items/41b4ec6bde794cbcd0f6
次(ベクトル編):https://qiita.com/hatuxes/items/c7b88a32e0a60ddd3e69
-
弧度法自体の定義はここでは必要としないため割愛した。 ↩
-