問題点
機械学習アルゴリズムを実装する際に、2つの行列$A, B \in \mathbb{R}^{n \times m}$の積のTrace$\mathrm{Tr}(A \cdot B^T)$を計算するシーンがよくあるが、定義通りnumpyのtraceを使うと非常に遅くて困る。
結論
SparseMatrixを使わないなら
np.einsum('ij,ij->', A, B)
がぶっちぎりで速く、SparseMatrixにも対応したいなら
np.sum(A * B)
がわりかし速い!
手法紹介
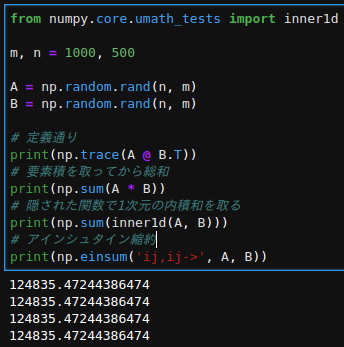
主に4パターンの計算方法がある(他にもあったらコメントください)。
A. 定義通り
np.trace(A @ B.T)
B. 要素積の総和
np.sum(A * B)
C. 秘められし関数inner1dで計算
from numpy.core.umath_tests import inner1d
np.sum(inner1d(A, B))
ただし、このinner1dはnumpyの内部で使われている関数なので推奨されていないようです(参照3)。
D. B.をアインシュタインの縮約記法で書けるeinsumで書く
np.einsum('ij,ij->', A, B)
アインシュタインの縮約記法を知らない方は参考の1.を参照してください。とても詳しくまとめてあります。ただし、この書き方はnumpy arrayのみでscipyのSparseMatrixには実装されていないです。ただ、実装する動きはあるようです(参照4)。
実験
環境
- Python 3.6.6 :: Anaconda custom (64-bit)
- numpy: 1.15.3
結果
ちゃんと同じ結果になるかを確認。
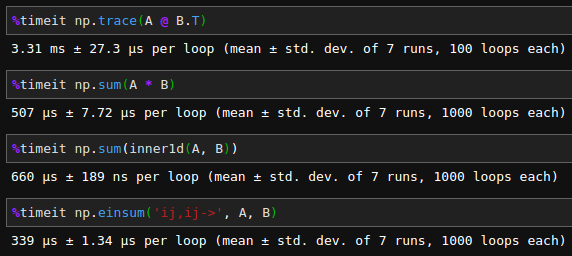
速度を%timeitで計測し比較。
Dが圧勝!定義通り計算するより10倍くらい速い!!ただ、上述したとおりeinsumはSparseMatrixでは使えないので、疎行列を扱う際にはBを使うのが良いという結論になりました。Bも定義通り計算するよりも6倍くらい速く、申し分ない結果になりました。
余談
行列の転置マーク$T$を右肩に書く派と左肩に書く派で流派が分かれていて論文読んでて混乱する。するよね?