はじめに
この記事はHoudini Advent Calender 2017の9日目の記事です。
ここで紹介するのは「データの見せ方」ではなく、データを可視化する手法と考え方になります。
紹介する内容ですが、せっかくならタイトル通りHoudiniならではのものにしたかったので、
ExcelやMayaで開発なしに出来てしまうような棒グラフや二次元空間での点・線のプロットは除外しました。
ということで今回紹介するのは、地球上のA地点→B地点への移動の軌跡を描くアニメーションです。
具体的な例で言うと、人の流れ、お金の流れ、通信、サイバー攻撃...等の可視化や、応用すれば何かの賑やかしにも使えそうです。
完成動画はこちら -> https://youtu.be/BuXSuRdy2Gw
一つ一つを細かく説明していくとかなり長くなってしまうので、HIPファイルを見れる前提で要所要所をかい摘んでざっくり解説していきます。
基本的なオペレーションやパラメータへのリンクを理解している前提で進めるのとVEXコードだらけなので、
多分Houdini中級者さんかコードに抵抗がない人向けです。
Houdini知らない方や初級者さんは、Houdiniってこういうこと出来るんだなーってくらいの感じで読んで頂ければと思います!
Houdini玄人さまは、、、もっといい手法があったり間違っていたらご指摘下さい。。
準備
HIP
HIPファイルはこちら
Houdiniのバージョンは16.5.268です。
データ
今回はData Driven Securityのデータmarx-geo.csvを改変して使うことにしました。改変後データはHIPと一緒に入っています。
データのライセンスはDDSから継承してクリエイティブ・コモンズ 表示 - 継承 4.0 国際 ライセンスになります。

地球テクスチャ
地球のテクスチャはBMNGを使用します。
今回は納品するわけでもないので、5kのjpgを使います。
こちらは配布データに含めていませんので各自ダウンロードをお願いします。
Display Option
HoudiniのDisplay Option > SceneからHDR Renderingにチェックを入れてください。
1以上の値を持つColorがViewに反映されるので光り物をやるときは便利です。
目的
CSVには日付時刻、始点・終点の緯度経度のデータが入っています。
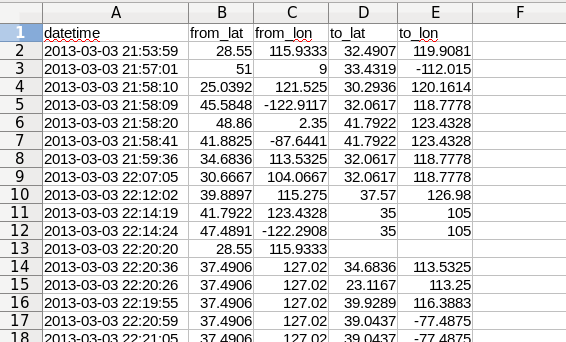
このデータをもとに、ポイントが時系列で始点から終点へ向かって尾を引きながら弧を描くように飛ぶ映像を作りたい。
最初にも張ってありますが、動画にするとこんな感じです。
https://youtu.be/BuXSuRdy2Gw
こういう感じです。
皆さんはこれを作るとき、どういう処理の流れを考えますか?
処理の流れ
僕はこういうフローを想定しました。
1.HoudiniにCSVを読み込む
2.緯度経度を球面座標に変換する
3.始点と終点を元に弧を描く
4.その弧を使って尾を引くポイントをパスアニメーションさせる
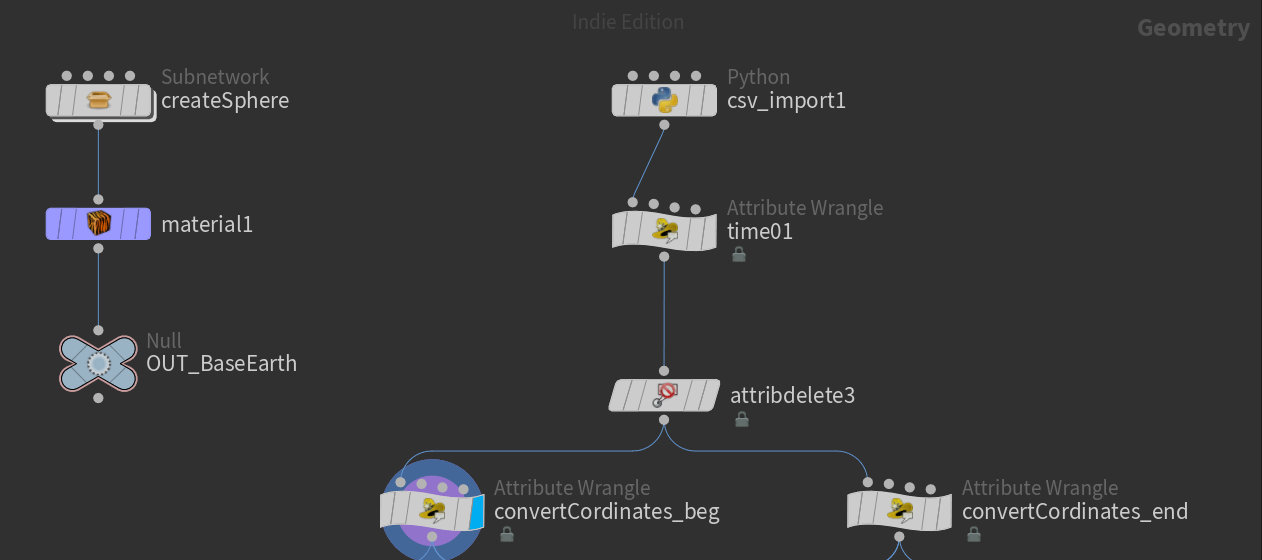
HoudiniにCSVを読み込む
Python SOPを使ってcsvを読み込み
※18/07/20追記
【Houdini】PythonSOPでのデータ読み込みコードの最適化
下記で紹介しているやり方はあまり効率的ではないので↑推奨です。
基本的にはPython SOPを使います。
HoudiniにはデフォルトでTable Import SOPというノード(中身はPython SOP)がありますが、あまり使っていません。
ちょっとしたデータの読み込みにはお手軽で良いのですが、項目数が多かったり、途中でCSVの形式が変わったりすると使いにくくなるんです。
それとデータを読み込んでアトリビュートを作成する段階で座標変換など何かしらの処理をしたかったりすると、結局はPython SOPを使うことになるので、それなら最初から という感じです。
読み込みたい項目は出発地点の緯度・経度、目標地点の緯度・経度、日付時刻の5つです。
読み込む以外にやりたいこととしては、
- これらの緯度経度には空欄が混ざっているのでその行を回避したい
- 日付時刻をHoudiniで扱い易くするためにUnixtimeに変更したい
という感じでしょうか。
実際にコードにするとこんな感じになりました。
※Python SOP上にcsvfile / restriction_maxrows / maxrowsというパラメータを作成して参照しています。

node = hou.pwd()
geo = node.geometry()
import csv
import time
import datetime
### csvから読んできた値の型変換
def convertType(target, type=""):
if type == "str":
return str(target)
elif type == "float":
try:
return float(target)
except ValueError:
return 0.0
elif type == "int":
try:
return int(target)
except ValueError:
return 0
### 型からデフォルト値を作成
def defaultValueFromType(value):
if isinstance(value, str):
return ""
elif isinstance(value, int):
return 0
elif isinstance(value, float):
return 0.0
### 日付時刻をUnixtimeに
def convertToUnixtime(strdatetime):
dates = strdatetime.split(" ")[0].split("-")
times = strdatetime.split(" ")[1].split(":")
dt = datetime.datetime(int(dates[0]), int(dates[1]), int(dates[2]), int(times[0]), int(times[1]), int(times[2]))
ut = int(time.mktime(dt.timetuple()))
return ut
### 行数制限
restriction = node.parm("restriction_maxrows").eval()
maxrows = node.parm("maxrows").eval()
### csv読み込み
csvpath = node.parm("csvfile").eval()
with open(csvpath, "rU") as f:
rows = [ row for row in csv.DictReader(f) ]
i = 0
valueDB = {}
attribDB = {}
### 行毎の処理
for row in rows:
if restriction == 1 and i > maxrows:
break
if row["datetime"] == "":
continue
### ポイント作成
point = geo.createPoint()
### 各項目からアトリビュート値の辞書作成
valueDB["time"] = convertType(row["datetime"], "str")
valueDB["utime"] = convertToUnixtime(row["datetime"])
valueDB["srclat"] = convertType(row["from_lat"], "float")
valueDB["srclon"] = convertType(row["from_lon"], "float")
valueDB["dstlat"] = convertType(row["to_lat"], "float")
valueDB["dstlon"] = convertType(row["to_lon"], "float")
### 初回のみアトリビュート作成
if i == 0:
for key in valueDB.keys():
defaultValue = defaultValueFromType(valueDB[key])
if defaultValue != "ERROR":
### アトリビュートオブジェクトの辞書作成
attribDB[key] = geo.addAttrib(hou.attribType.Point, key, defaultValue)
### キーからアトリビュートオブジェクトと値を呼び出し、セット
for key in valueDB.keys():
point.setAttribValue(attribDB[key], valueDB[key])
i += 1
CSVの読み込みやdt/ut変換などはネット上に分かりやすいページが沢山あるので割愛します。
ここの書き方は結構人によって変わってくるような気がしますが、個人的なオススメポイントとしては、
add/setAttribは一行ずつ書かず、アトリビュートオブジェクト/値を辞書型にして同じキーをもたせるという所でしょうか。
これもデータの項目数が多かったり項目が途中で変わったりすると、書きなおすのが面倒・コードが読みにくくなるのを回避する為です。
特にjsonやxmlのようなデータを扱う場合は顕著ですね。
HDA化して複数のデータを扱うような場合はキー作成のところをパラメータとして表に出したり、
予め全キー分の処理を書いておいてsetAttribするときにtry/exceptでKeyErrorをパスするなどで汎用化しやすくなります。
...と書いておいて何ですが、そもそもデータの項目数が沢山ある場合はpandas等を使ったほうが良いような気がします。
データを全行読むと重いので、とりあえず100行で制限して進めて行きます。
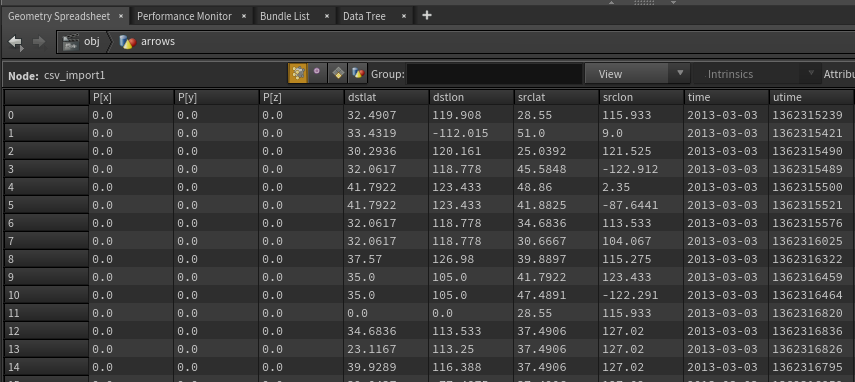
Geometry Spreadsheetを確認すると出発地点・目標地点の緯度経度、時間が読み込めていることが分かります。
ここからはAttribute Wrangleの出番です。
時間のスケール
時間データを更に扱い易くするために、整数時間をFloatの0-1にスケールします。
@time01 = fit(float(i@utime), float(chi("Time_Min")), float(chi("Time_Max")), 0.0, 1.0);
最小値、最大値は自動で取ってもいいんですが、データが変わった時に結果が変わってしまうので手動で設定することが多いです。
時間のデータがない場合はptnumとnumptでもポイント番号順に時間データを作成できます。
緯度経度を球面座標に変換
地球の半径と緯度経度から球面座標が計算できます。
出発地点用、目標地点用でコードを使いまわしたいので、アトリビュート名をパラメータにしてあります。
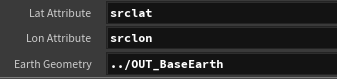
# include <math.h>
//16.5ではincludeせずともPIのみで円周率が取れるようです。
// 地球の半径を取得
string earthpath = concat("op:", opfullpath(chs("Earth_Geometry")));
vector bbox = getbbox_size(earthpath);
float r = bbox.x / 2;
// パラメータに入力したアトリビュート名から緯度経度を取得
float lat = point(0, chs("Lat_Attribute"), @ptnum);
float lon = point(0, chs("Lon_Attribute"), @ptnum);
// 緯度経度を最低値を基準にラジアンに変換
float radlat = fit(lat, -90, 90, 0, M_PI);
float radlon = fit(lon, -180, 180, 0, M_PI * 2);
// ラジアンに変換した緯度経度を球面座標に変換
vector pos;
pos.x = sin(radlat) * cos(radlon) * r;
pos.z = sin(radlat) * sin(radlon) * r;
pos.y = cos(radlat) * r;
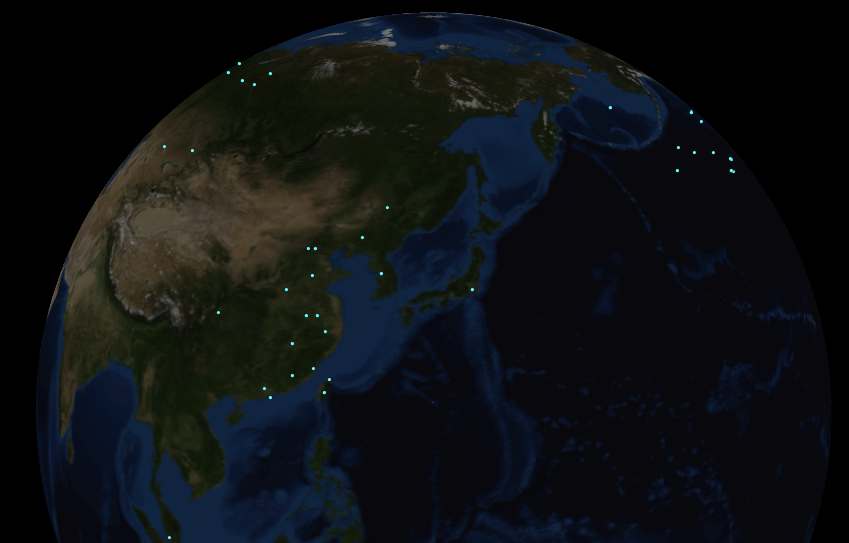
@P = set(-pos.x, -pos.y, pos.z);
ここで初めてViewに変化がありました!ポジションに緯度経度から変換された球面座標が入りました。
ベースカーブの作成
球面上に弧を描く
特にここからのアプローチの仕方は沢山あると思います。
今回は球面上の二点から弧を描く手法として、「二点の距離を直径とした円の弧を描く」という手法を取りました。
これのメリットとしては、兎に角綺麗に弧が描けるのと、絶対にラインが球にめり込まないという所です。
流れとしては、
始点と終点の距離から弧の長さを計算し、その長さを元に分割を決めて、
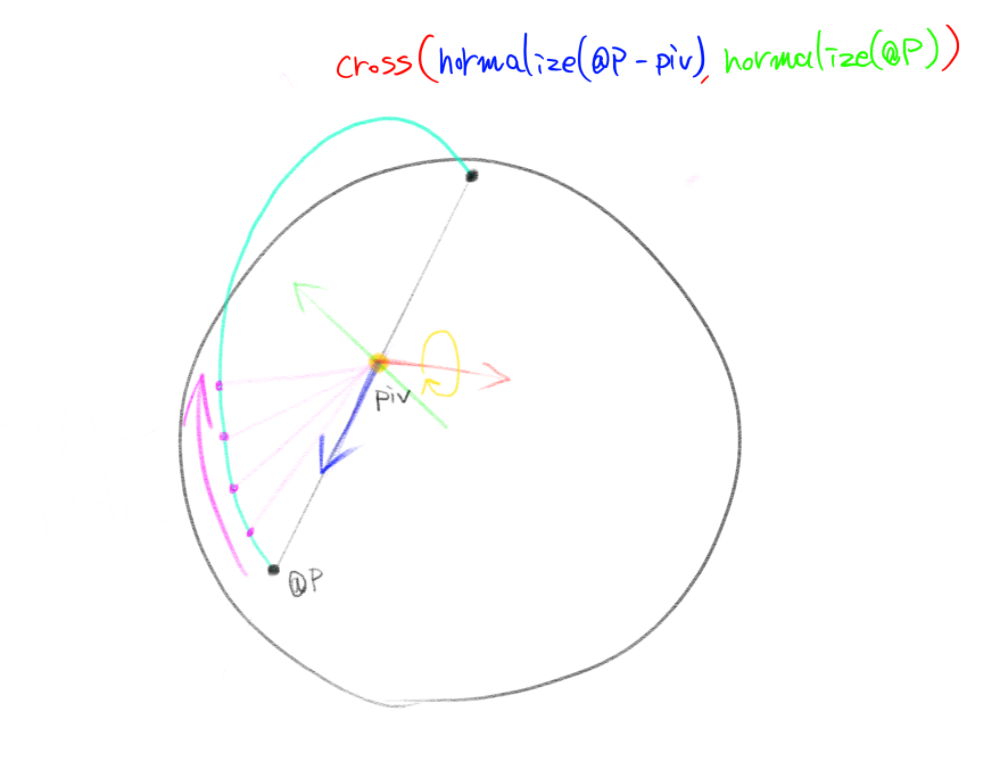
始点と終点の中間を基点として、基点から始点へのベクトルと原点から基点へのベクトルの外積を回転軸とし、
その軸で行列を回転させて弧を描く という感じです。
# include <math.h>
// 分割モード
int mode = chi("Mode");
int segs = chi("Segments");
float segdist = chf("Distance_Per_Segment");
// 直線距離と孤の長さ
float linerdist = distance(@P, v@opinput1_P);
float arcdist = 2 * M_PI * (linerdist / 2) * (180.0 / 360.0);
// 分割距離・分割数の算出
if (mode == 0){
segdist = arcdist / segs;
}else if (mode == 1){
segs = int(arcdist / segdist);
}
// 分割毎のラジアン
float rad_per_seg = radians(180.0 / segs);
addpointattrib(0, "curveu", -1.0);
setpointattrib(0, "curveu", @ptnum, 0.0, "set");
// Polylineを作成して始点を追加
int prim = addprim(0, "polyline");
addvertex(0, prim, @ptnum);
matrix3 m = ident(); // 単位行列の作成
vector piv = (@P + v@opinput1_P) / 2; // 始点と終点の中間地点をピボットに
vector diff = @P - piv; // 始点からピボットまでの距離
vector axis = cross(normalize(@P - piv), normalize(piv)); // ピボットから始点へのベクトルと原点からピボットへのベクトルの外積を回転軸とする
int newpt;
float weight;
vector newpos;
for (int i = 0; i < segs; i++){
weight = float(i) / segs; // 0~1
rotate(m, rad_per_seg, axis); // 行列を回転
newpos = diff * m + piv; // ポジションに回転を適用
newpt = addpoint(0, newpos);
addvertex(0, prim, newpt);
setpointattrib(0, "curveu", newpt, weight, "set");
}
addprimattrib(0, "time01", -1.0);
setprimattrib(0, "time01", prim, f@time01, "set");
addprimattrib(0, "segdist", 0.0);
setprimattrib(0, "segdist", prim, segdist);
addprimattrib(0, "arcdist", 0.0);
setprimattrib(0, "arcdist", prim, arcdist);
弧をスケール
よくある話ですが、↑で作った弧をもっと低くして欲しいという要求がありました。
そこで色々なアプローチを試したのですが、一度回転をなくしてスケールする方法が一番綺麗に、直感的にスケールすることが出来ました。
線が地球にめり込まずに調整しやすいように、弧の長さをスケールにリマップ出来るようにしています。
// 始点と終点
int prim = int(pointprims(0, @ptnum)[0]);
int primpts[] = primpoints(0, prim);
int begpt = primpts[0];
int endpt = primpts[-1];
vector begpos = point(0, "P", begpt);
vector endpos = point(0, "P", endpt);
vector pos = @P;
// 原点に移動
pos -= begpos;
endpos -= begpos;
// 二軸回転を復元
matrix3 m_rot = dihedral(normalize(endpos), {1, 0, 0});
pos *= m_rot;
// ロールを復元
vector pos1 = point(0, "P", neighbour(0, begpt, 0));
vector axis_x = {1, 0, 0};
vector axis_y = normalize(pos1) * m_rot;
vector axis_z = cross(axis_x, axis_y);
matrix3 m_roll = dihedral(axis_z, {0, 0, 1});
pos *= m_roll;
// 孤の長さからスケールを算出
float arcdist = prim(0, "arcdist", prim);
vector scale = set(1, fit(arcdist, chf("Arcdist_Min"), chf("Arcdist_Max"), chf("Scale_Min"), chf("Scale_Max")), 1);
// スケールを適用
matrix scalem = ident();
scale(scalem, scale);
pos *= scalem;
// 復元した回転を戻す
pos *= invert(m_roll);
pos *= invert(m_rot);
// 初期位置に戻す
@P = begpos + pos;
キャッシュをとる
この先ほぼ時間依存1な処理になってくるので、一旦ここでキャッシュを取ります。
ローカル作業だけならあまり変わりませんが、サーバーに投げてIFD生成やアニメーション部分のキャッシュを何回も計算する場合、
ここでキャッシュをとっておくだけでリソースも時間も節約できます。
キャッシュを取る前に、いらないアトリビュートは消しておきましょう。
Colorなどの軽くてよく弄るようなノードはキャッシュ後に追加すると良いです。
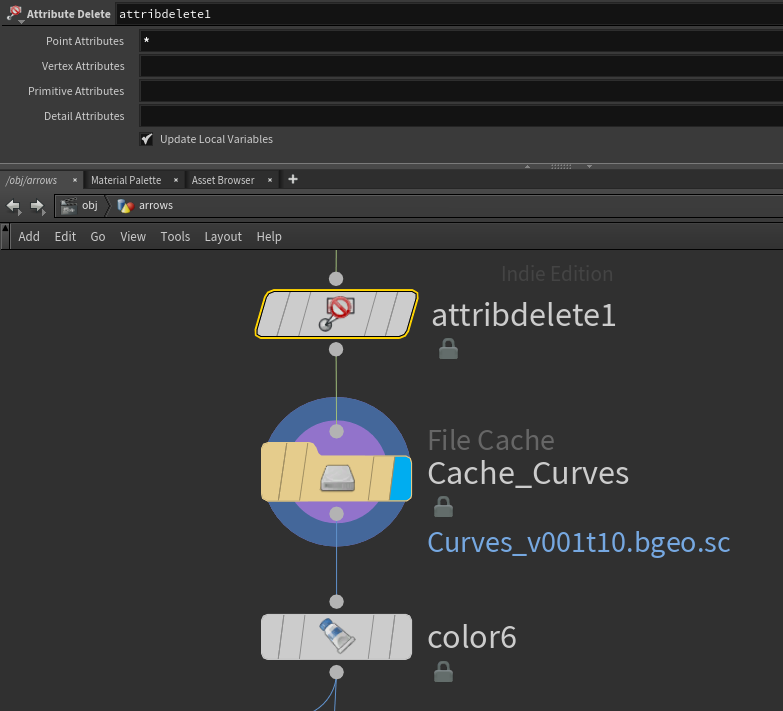
これでベースカーブの作成は完了です!
アニメーションのための事前処理
ポイント生成
Houdiniはジオメトリの生成より削除のほうが負荷が高いようで、特にTime Dependentな処理の場合、WrangleでもBlastでもDeleteでも処理速度の足を引っ張っていることが多い気がします。
なので極力ジオメトリ削除の処理はTime Dependent外で行いたいというわけです。
そこで今回はカーブの本数と同じだけ、必要なアトリビュートを持たせたポイントを生成し、カーブは削除します。
int newpt = addpoint(0, {0, 0, 0});
addpointattrib(0, "time01", 0.0);
setpointattrib(0, "time01", newpt, f@time01, "set");
addpointattrib(0, "segdist", 0.0);
setpointattrib(0, "segdist", newpt, f@segdist, "set");
addpointattrib(0, "arcdist", 0.0);
setpointattrib(0, "arcdist", newpt, f@arcdist, "set");
addpointattrib(0, "Cd", {0, 0, 0});
setpointattrib(0, "Cd", newpt, @Cd, "set");
removeprim(0, @primnum, 1);
トレースアニメーション
アニメーション制御のために諸々パラメータを作り、さっき作ったポイント毎にラインを生成する処理を走らせます。
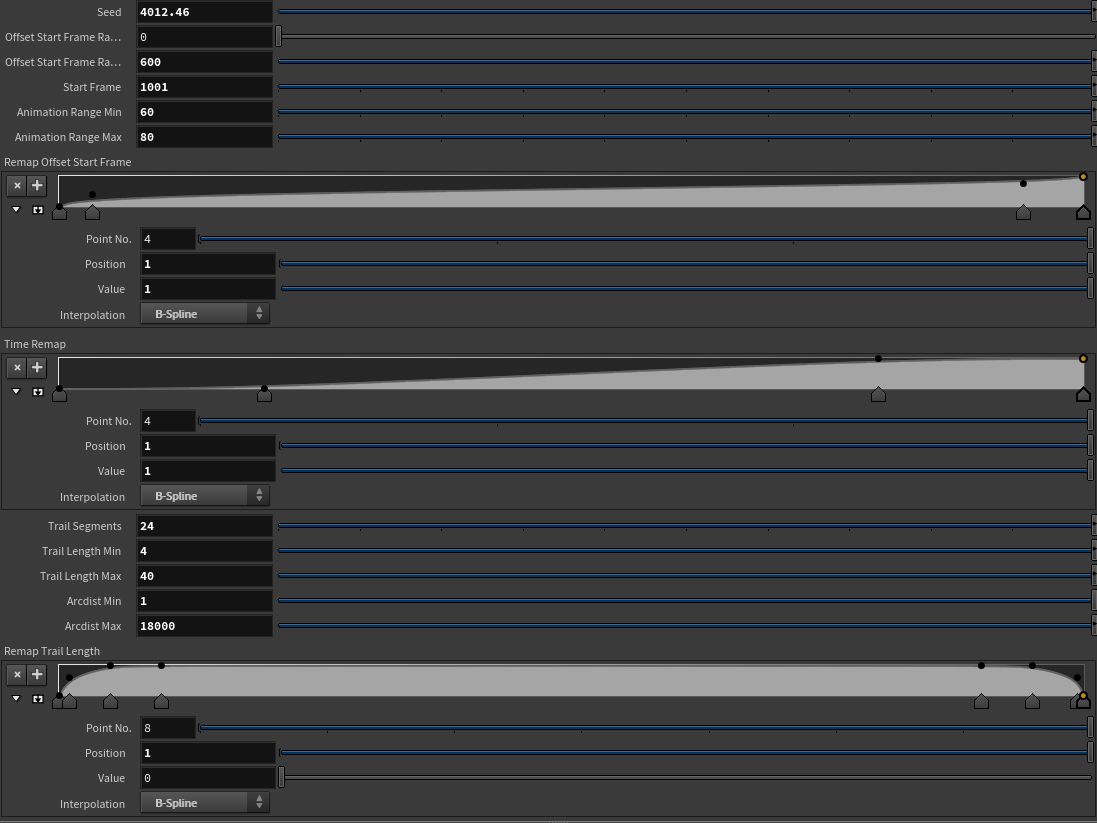
float seed = chf("Seed"); //シード値
int startFrame = chi("Start_Frame"); //開始フレーム
float offsetStartFrameMin = chf("Offset_Start_Frame_Rand_Min"); //最初のアニメーションのオフセットフレーム数
float offsetStartFrameMax = chf("Offset_Start_Frame_Rand_Max"); //最後のアニメーションのオフセットフレーム数
int animRangeMin = chi("Animation_Range_Min"); //一本辺りのアニメーションの最短レンジ
int animRangeMax = chi("Animation_Range_Max"); //一本あたりのアニメーションの最長レンジ
float offsetPP = chramp("Remap_Offset_Start_Frame", f@time01); //開始フレームのオフセット用に正規化された時間をリマップ可能にする
float offsetStartFramePP = fit01(offsetPP, offsetStartFrameMin, offsetStartFrameMax); //リマップされた値を元にオフセットフレーム数を算出
float startFramePP = startFrame + offsetStartFramePP; //スタートフレームにオフセットフレームを足してライン毎の開始フレームを決める
float localFrame = clamp(@Frame - startFramePP, 0, 10000); //現在のフレームから開始フレームを引きマイナスの値を切り落とし、ローカル時間を作る
int animRange = int(fit01(rand(@ptnum + seed * 6.187), animRangeMin, animRangeMax)); //ランダムでアニメーションレンジを決める
float animtime01 = clamp(localFrame / animRange, 0, 1); //ローカル時間を01に正規化する
animtime01 = chramp("Time_Remap", animtime01); //ローカル時間をリマップ可能にする
// Trail
int trailSegs = chi("Trail_Segments"); //Trailの分割数
float trailLengthMin = chf("Trail_Length_Min"); //Trailの最短の長さ
float trailLengthMax = chf("Trail_Length_Max"); //Trailの最長の長さ
float arcdistMin = chf("Arcdist_Min"); //弧の最短の長さ
float arcdistMax = chf("Arcdist_Max"); //弧の最長の長さ
float trailLength = fit(@arcdist, arcdistMin, arcdistMax, trailLengthMin, trailLengthMax); //Trailの長さを孤の長さを元に算出
trailLength = @segdist / @arcdist * trailLength; //Trailの長さを正規化
vector pos;
float trail, trailu;
int newpt;
int trailprim = addprim(0, "polyline");
float trailLengthMultipler = chramp("Remap_Trail_Length", animtime01); //正規時間を元にTrailの長さをリマップ可能にする
vector color = prim(1, "Cd", @ptnum); //色を転写
addpointattrib(0, "trailu", 0.0);
//Trailの分割数だけループを回す
for (int i = 0; i <= trailSegs; i++){
trailu = float(i) / trailSegs;
trail = animtime01 - trailLength * trailLengthMultipler * trailu; //ループごとにanimtime01をずらしていく
pos = primuv(1, "P", @ptnum, set(trail, 0, 0)); //ずらしたanimtime01を元にベースカーブからポジションを取得
//ループ初回のみ位置はそのまま
if (i == 0){
@P = pos;
newpt = @ptnum;
setpointgroup(0, "headGP", newpt, 1, "set");
}else{
newpt = addpoint(0, pos);
}
addvertex(0, trailprim, newpt);
setpointattrib(0, "Cd", newpt, color, "set");
setpointattrib(0, "trailu", newpt, trailu, "set");
setpointattrib(0, "animtime01", newpt, animtime01, "set");
}
後処理
alphaとpscale
いよいよ終盤です。方向感、飛んでる感、軌跡感を出すために頭から尻尾にかけてAlphaとPscaleの値を減衰させます。
float pscale = chf("Pscale");
@Alpha = 0.9 - @trailu;
@pscale = pscale * chramp("Remap_Pscale", @trailu);
Cutoff
アニメーションしていないポイントは必要ないので削除します。
if (@animtime01 == 0.0 || @animtime01 == 1.0){
removepoint(0, @ptnum);
}
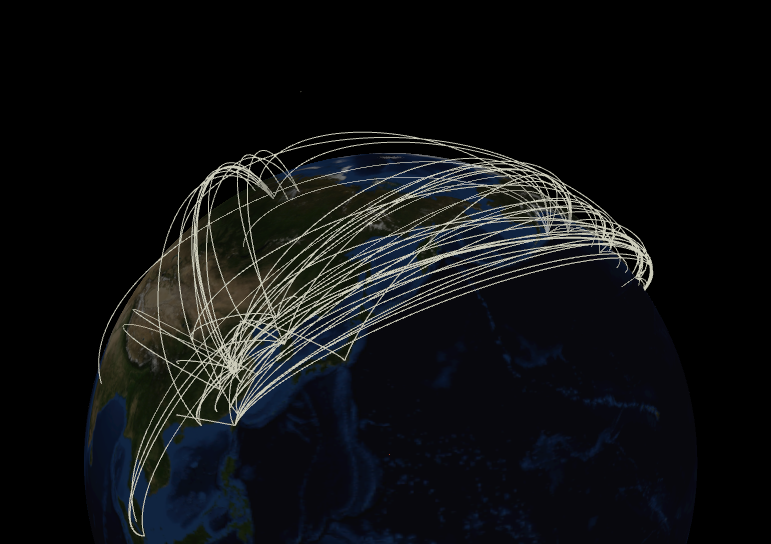
かんせい
Constantマテリアルを当てて完成です!お疲れ様でした。
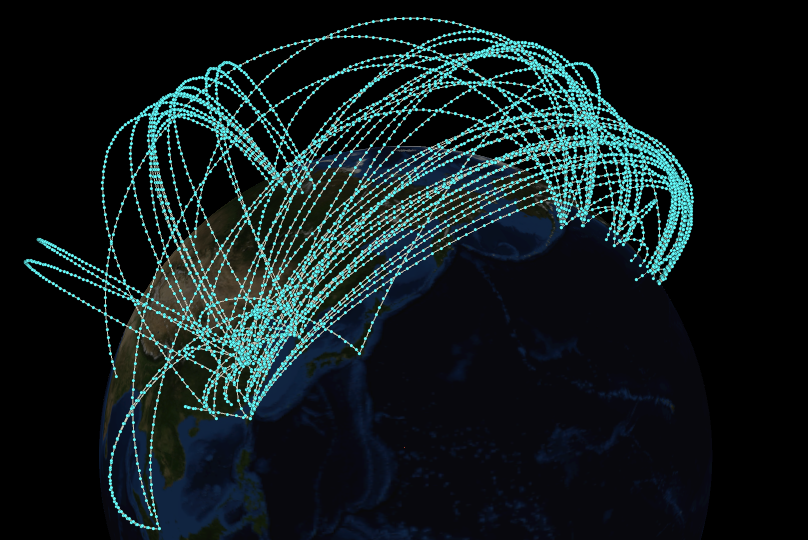
10万行読んでみましょう。

見事に混沌としていますね。
ノードは結構コンパクトになりました。
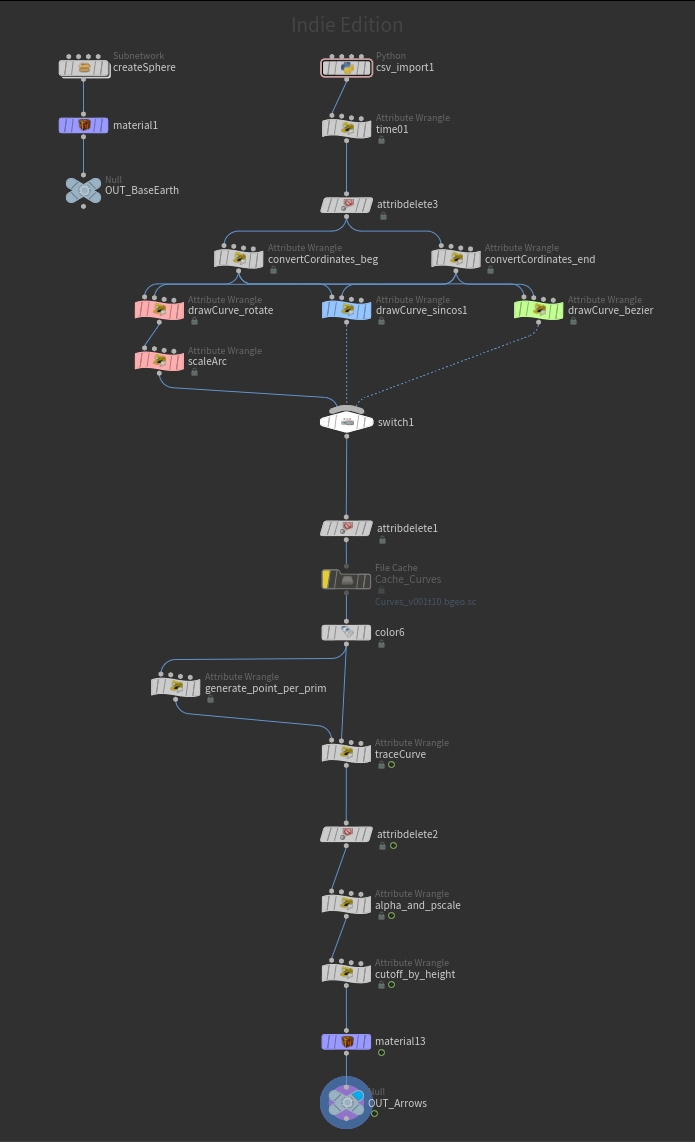
ここから更に頭に矢印を追加したり、着地した時に波紋エフェクトを生成したり、
今回は緯度経度と時間だけのデータでしたが、付加情報がある場合色分けしたり、文字を出したり、スピードを変えたり、、と無限に派生できます!
おまけ
記事を書いている途中にスケール出来る弧の描画の仕方を2つほど思いついたので、記事中で紹介した手法をAとして比較してみました。
手法B
単純に原点でsin/cosで半円を描いてスケール>回転>移動を適用するもの。記事中で紹介した手法よりとてもシンプルで簡単・・。これでいいのでは??
# include <math.h>
// 分割モード
int mode = chi("Mode");
int segs = chi("Segments");
float segdist = chf("Distance_Per_Segment");
// 直線距離と孤の長さ
float linerdist = distance(@P, v@opinput1_P);
float r = linerdist / 2;
float arcdist = 2 * M_PI * r * (180.0 / 360.0);
// 分割距離・分割数の算出
if (mode == 0){
segdist = arcdist / segs;
}else if (mode == 1){
segs = int(arcdist / segdist);
}
addpointattrib(0, "curveu", -1.0);
setpointattrib(0, "curveu", @ptnum, 0.0, "set");
int prim = addprim(0, "polyline"); // Polylineを作成
vector piv = avg(@P, v@opinput1_P); // 始点と終点の中間をピボットに
// 回転行列の作成
matrix3 rotm = dihedral({1, 0, 0}, normalize(v@opinput1_P - @P)); // X軸を始点から終点へのベクトルに合わせる回転行列の作成
matrix3 rollm = dihedral({0, 1, 0} * rotm, normalize(piv)); // 回転後のY軸を原点からピボットへのベクトルに合わせる回転行列の作成
// スケール用の行列の作成
vector scale = set(1, fit(arcdist, chf("Arcdist_Min"), chf("Arcdist_Max"), chf("Scale_Min"), chf("Scale_Max")), 1); // 孤の長さからスケール値を算出
matrix3 scalem = ident(); // 単位行列
scale(scalem, scale); // 行列をスケール
int newpt;
float weight;
vector newpos;
for (int i = 0; i <= segs; i++){
weight = float(i) / segs; // 0~1
newpos = set(cos(weight * M_PI) * r + r, sin(weight * M_PI) * r, 0); // 0~1に対応する半円弧の位置を取得
newpos *= scalem * rotm * rollm; // スケール・ZY回転・X回転の順で適用
newpos += @P; // 原点から始点へ移動
newpt = addpoint(0, newpos); // 計算した位置にポジションを追加
addvertex(0, prim, newpt);
setpointattrib(0, "curveu", newpt, weight, "set");
}
addprimattrib(0, "time01", -1.0);
setprimattrib(0, "time01", prim, f@time01, "set");
addprimattrib(0, "segdist", 0.0);
setprimattrib(0, "segdist", prim, segdist);
addprimattrib(0, "arcdist", 0.0);
setprimattrib(0, "arcdist", prim, arcdist);
removepoint(0, @ptnum); // 初期ポイントは使わないので削除
手法C
お次は最近Twitterでよく見かけたベジェ曲線
綺麗な半円にはならないですが、めり込みはなく結構いい感じになりました!
こっちの手法だと形状の制御がしやすいので、形を弄りたい時にはいいかもしれません。
# include <math.h>
// 三次ベジェ曲線の関数 二点のポジションとハンドル、0-1のuを渡すとu地点の位置を返す
vector bezier3(vector pos1, pos2, handle1, handle2; float u)
{
u = clamp(u, 0, 1);
float ru = 1 - u;
vector pos;
pos.x = pow(ru,3)*pos1.x + 3*pow(ru,2)*u*handle1.x + 3*ru*pow(u,2)*handle2.x + pow(u,3)*pos2.x;
pos.y = pow(ru,3)*pos1.y + 3*pow(ru,2)*u*handle1.y + 3*ru*pow(u,2)*handle2.y + pow(u,3)*pos2.y;
pos.z = pow(ru,3)*pos1.z + 3*pow(ru,2)*u*handle1.z + 3*ru*pow(u,2)*handle2.z + pow(u,3)*pos2.z;
return pos;
}
// 分割モード
int mode = chi("Mode");
int segs = chi("Segments");
float segdist = chf("Distance_Per_Segment");
// 直線距離と孤の長さ
float linerdist = distance(@P, v@opinput1_P);
float arcdist = 2 * M_PI * (linerdist / 2) * (180.0 / 360.0);
// 分割距離・分割数の算出
if (mode == 0){
segdist = arcdist / segs;
}else if (mode == 1){
segs = int(arcdist / segdist);
}
addpointattrib(0, "curveu", -1.0);
setpointattrib(0, "curveu", @ptnum, 0.0, "set");
// Polylineを作成して始点を追加
int prim = addprim(0, "polyline");
addvertex(0, prim, @ptnum);
float handleweight = chf("Handle_Weight"); // ハンドルの傾きのウェイト値
float heightmult = fit(arcdist, chf("Arcdist_Min"), chf("Arcdist_Max"), chf("Height_Min"), chf("Height_Max")); // 孤の長さからハンドルの長さを算出
vector piv = avg(@P, v@opinput1_P); // 始点と終点の中間をピボットとする
vector beghandle = @P + (normalize(@P) * (1 - handleweight) + normalize(piv) * handleweight) * heightmult; // 始点のハンドル
vector endhandle = v@opinput1_P + (normalize(v@opinput1_P) * (1 - handleweight) + normalize(piv) * handleweight) * heightmult; // 終点のハンドル
int newpt;
float weight;
vector newpos;
for (int i = 0; i <= segs; i++){
weight = float(i) / segs;
newpos = bezier3(@P, v@opinput1_P, beghandle, endhandle, weight); // 三次ベジェ関数を使って弧のポジションを取得
newpt = addpoint(0, newpos);
addvertex(0, prim, newpt);
setpointattrib(0, "curveu", newpt, weight, "set");
}
addprimattrib(0, "time01", -1.0);
setprimattrib(0, "time01", prim, f@time01, "set");
addprimattrib(0, "segdist", 0.0);
setprimattrib(0, "segdist", prim, segdist);
addprimattrib(0, "arcdist", 0.0);
setprimattrib(0, "arcdist", prim, arcdist);
計測結果
10万本のラインをサンプル数50で生成してトランスフォームを掛ける速度を計測しました。

| 手法A(rotate) | 手法B(sincos) | 手法C(bezier) |
|---|---|---|
| 2.591s | 1.217s | 1.415s |
| ※手法Aの秒数はdrawCurve_rotateノードとscaleArcノードの合計値です。 |
手法Bが一番早いですね!!
手法Aの倍以上の速度で処理も1ノードに纏まっていい感じです。
こんな感じで目的に合わせて色々な手法をテスト・比較して最適化していくのがとてもやりやすいのでHoudini最高ですね!
ただほどほどにしないと本来の仕事が全然進まないのでご注意・・。
まとめ
Houdiniでは一つのことをするのに沢山の手法がありますが、Wrangleにしても他のSOPノードにしても、時間依存1な部分とそうでない部分の切り分けが大切だと思っています。
使いにくくない程度にノードや手順が増えたとしても、極力時間に依存する処理は減らし、それ以外は事前処理としてキャッシュする という感じでシーン構築していくと効率が良いです。
逆に時間に依存しない部分は、多少速度を犠牲にしてもメンテナンス性や作業コストを重視したほうがいいでしょう。
ながーくなってしまいましたが、最後まで読んでいただきありがとうございました!