はじめに
この1ヵ月程度,大学院での研究のために複雑ネットワークの勉強しており,実際のデータを用いてネットワーク分析で遊んでみたいなと思いました.
どのようなデータを用いてネットワーク分析を行おうか考えていたとき@fufufukakakaさんの記事を見つけ,自分がにじさんじのライバーさんの配信をよく視聴することもあり,同じようなネットワーク分析がしてみたいなと思い立ちました.
しかし,元の記事のような高度なスクレイピングを応用するには自身の技術が足りないので,今回はもっと簡単に,にじさんじ非公式wikiから有志の方によってまとめられたにじさんじライバー間のコラボ一覧表をお借りして,にじさんじライバーのコラボ関係ネットワークを作成しそれを分析してみることにしました.
目標
- テーブルデータのスレイピング・処理の練習
- ネットワーク分析(Python/networkx)の使い方を学ぶ
- ネットワーク分析の観点から,ライバー間のコラボ関係ネットワークについて,どのようなことが言えるのか考える
実装
今回の実装は以下の4つの手順で実装していきます.
- 必要なパッケージのインポート
- にじさんじ非公式wikiからコラボ一覧表をスクレイピング
- ライバー間のコラボ関係のネットワークを作成
- ネットワーク分析
1. 必要なパッケージのインポート
まず必要なパッケージをインポートしていきます
# パッケージのインポート
import requests
from bs4 import BeautifulSoup
import itertools
import networkx as nx
今回使ったpythonとパッケージのバージョンは以下の通りです
python == 3.8.8
requests == 2.25.1
beautifulsoup4 == 4.9.3
2. にじさんじ非公式wikiからコラボ一覧表をスクレイピング
今回,ネットワーク作成に使わせていただくコラボ一覧表はテーブルデータでまとめられているので,スクレイピングしてデータを取ってきます.今回スクレイピングを行うために使ったコードはこの本で解説されていたコードを参考にしました(というかほぼそのまま使ってます).
# URL(にじさんじ非公式wiki)
url = "https://wikiwiki.jp/nijisanji/コラボ一覧表"
# URLからページ内容を取得
r = requests.get(url)
html_contents = r.text
# HTML構文解析
html_soup = BeautifulSoup(html_contents)
# コラボ一覧表のテーブルを抽出
combi_table = html_soup.find("div", class_="wikiwiki-tablesorter-wrapper").find("table")
# テーブルの項目名の抽出
headers = []
for header in combi_table.find("tr").find_all("th"):
headers.append(header.text)
# 最初の行(項目名)以降の行に対して処理(各コラボの 人数/コラボ名/詳細の有無/メンバー の抽出)
values = []
for row in combi_table.find_all("tr")[1:]:
temp_list = [] # 一時格納用リスト
# th:コラボ名, td:それ以外の情報
for col in row.find_all(["th", "td"]):
temp_list.append(col.text)
values.append(temp_list)
上のコードを実行すると,コラボ一覧表をそのままスクレイピングできます.しかし,コラボのメンバーからネットワークを作成するには,データの処理が必要になります.
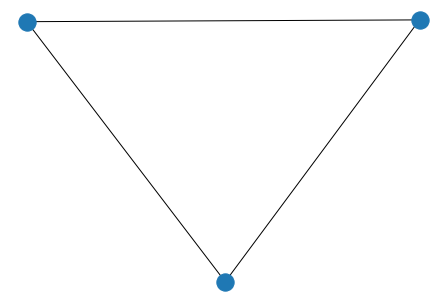
例えば,JK組(月ノ美兎・静凛・樋口楓(敬称略))の3人の場合,以下のように人名を数値に変換し,その数値の組み合わせを考える必要があります.
月ノ美兎 → 1, 静凛 → 2, 樋口楓 → 3
この場合考えられる数値の組み合わせは
(1,2), (1,3), (2,3)
実際にnetworkxを用いて,高度に抽象化されたJK組を描いてみます.
import networkx as nx
import matplotlib.pyplot as plt
G = nx.Graph()
# ノード数:3 の無向ネットワークを作成
G.add_nodes_from([1, 2, 3])
# 月ノ美兎 -> 静凛 へのリンク
G.add_edge(1, 2)
# 月ノ美兎 -> 樋口楓 へのリンク
G.add_edge(1, 3)
# 静凛 -> 樋口楓 へのリンク
G.add_edge(2, 3)
# 可視化
nx.draw(G)
plt.show()
今回は,先ほどスレイピングしたデータからコラボしているライバー名(にじさんじ外のVTuberの方も含む)で重複を避けるためにセットを作り,名前に順に数値を振っていき,コラボしている方同士の組み合わせを導出することで,どのライバー同士がコラボ経験があるのかを,上記のJK組の例のように2つの数値の組 (i,j) で表していきます.
# 名前を数値に置換していく
s = set()
name_to_int = {}
# コラボしたメンバーの重複なしのセットを作成
for i in range(len(values)):
for name in values[i][3].split(", "):
s.add(name)
# 作成したセットから各メンバーの名前に番号を振る
for name, i in zip(s, range(1, len(values)+1)):
s_dict = {name:i}
name_to_int.update(s_dict)
# コラボしたメンバーに対応する数値の組を作っていく
for i in range(len(values)):
temp_list = []
combi = []
for name in values[i][3].split(", "):
number = name_to_int[name]
temp_list.append(number)
for pair in itertools.combinations(temp_list, 2):
combi.append(pair)
values[i][3] = combi
# 後でネットワークノードにラベルを付けるための辞書
int_to_name = {v:k for k, v in name_to_int.items()}
今回は,先ほどスレイピングしたデータからコラボしているライバー名(にじさんじ外のVTuberの方も含む)で重複を避けるためにセットを作り,名前に順に数値を振っていき,コラボしている方同士の組み合わせを導出することで,どのライバー同士がコラボ経験があるのかを,上記のJK組の例のように2つの数値の組 (i,j) で表していきます.
# 名前を数値に置換していく
s = set()
name_to_int = {}
# コラボしたメンバーの重複なしのセットを作成
for i in range(len(values)):
for name in values[i][3].split(", "):
s.add(name)
# 作成したセットから各メンバーの名前に番号を振る
for name, i in zip(s, range(1, len(values)+1)):
s_dict = {name:i}
name_to_int.update(s_dict)
# コラボしたメンバーに対応する数値の組を作っていく
for i in range(len(values)):
temp_list = []
combi = []
for name in values[i][3].split(", "):
number = name_to_int[name]
temp_list.append(number)
for pair in itertools.combinations(temp_list, 2):
combi.append(pair)
values[i][3] = combi
# 後でネットワークノードにラベルを付けるための辞書
int_to_name = {v:k for k, v in name_to_int.items()}
3. ライバー間のコラボ関係のネットワークを作成
手順2.までで,ネットワークの作成に必要なデータは揃ったので,ここからは実際にコラボ関係のネットワークを作成していきます.
今回は簡単のために,コラボの回数に関わらず,(コラボ一覧表に乗っている限りで)一度でもコラボしたことがあるライバー同士をリンクでつなぐようなネットワークを作っていきます.スクレイピングしたままのデータをそのまま使っているのでにじさんじ外のVTuberの方やYouTuberの方も含まれています.
# ネットワークグラフの作成
G = nx.Graph()
G.add_nodes_from(list(range(1, len(s)+1)))
for i in range(len(values)):
for edge in values[i][3]:
G.add_edge(edge[0], edge[1])
# 各ノードにラベルを付与
H = nx.relabel_nodes(G, int_to_name)
# Gephi用にGraphML形式に変換
nx.write_graphml_lxml(H, "nijisanji_combi.graphml")
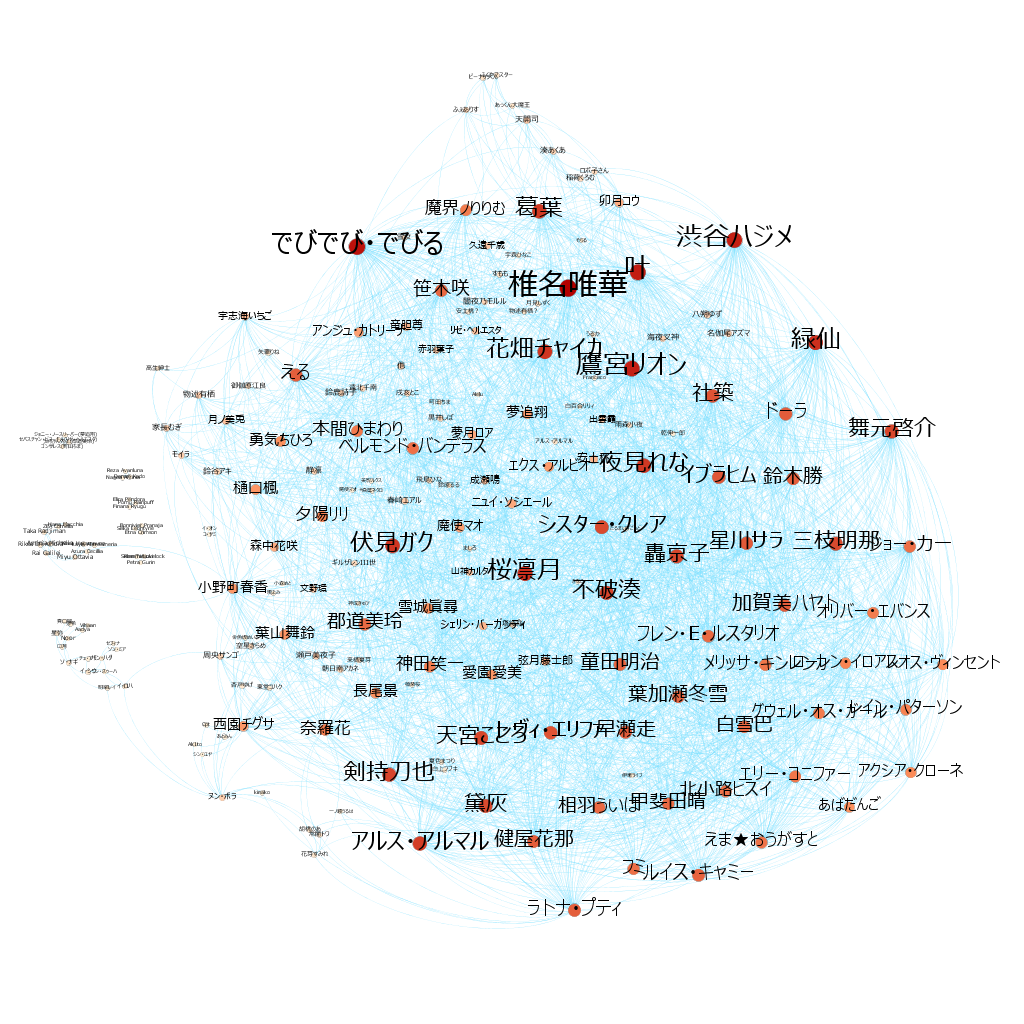
これでネットワークを作成することができました.ネットワーク分析用のソフトのGephiを用いて見やすく可視化していきます.
コラボしたことがある人数が多いほどノードが赤く大きくなり,名前が大きく表示されるように調整をしています.この画像だけでも,色々と興味深いことがわかります.
4. ネットワーク分析
ここからは作成したネットワークから情報を抽出していきます.ただし,自分がまだ複雑ネットワークの知識にまだまだ乏しく,すべての指標を理解できるわけではないので,解釈が簡単なネットワークの指標のいくつかを用いて,コラボ関係のネットワークから得られる情報を考えていきます.
4.1 平均次数
平均次数は,1つのノードに対して張られているリンクの平均を表します.今回の場合,平均次数は「ライバーがコラボしたことのある平均人数」を表します.
Deg_list = [d for n, d in H.degree()]
ave_deg = sum(Deg_list)/len(Deg_list)
print(ave_deg)
結果:
26.778846153846153
なので,平均26-7人とコラボしたことがあるということがわかります.
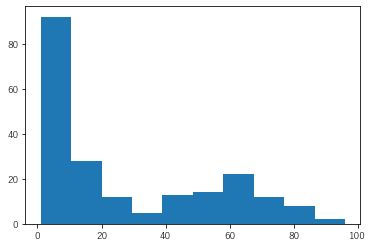
簡単ですが,次数のヒストグラムも描いてみます.
plt.hist(Deg_list)
plt.show()
ヒストグラムでは,コラボしたことがある人数が10人以下程度の人が多いという結果が出ていますが,これは今回ネットワーク分析に使用したデータに,にじさんじ外のVTuber・YouTuberの方が入ってしまっていることが原因だと考えられます.それを考慮すると,次数の中央値は60あたりにありそうです.
4.2 クラスター係数
クラスター係数は,(誤解を恐れず)簡単に言ってしまえば「友達の友達が自分の友達である度合」を表す指標です.今回の場合,「どれくらい広くコラボが行われているか」ということを示す指標の1つになります.
nx.average_clustering(H)
結果:
0.7149598722607242
あまり比較にはなりませんが,現実に存在するネットワークのクラスター係数は0.1から0.7程度らしいです(wikipedia:複雑ネットワーク).
このことからにじさんじのコラボ関係ネットワークのクラスター係数はそこそこ高く,コラボ時のメンバーに偏りが少なくに広くコラボがやられてきたということがわかります.
このあたりは「にじさんじ甲子園」や「にじさんじマリカ杯」,最近では「CRカップ」や「Ark」といった大規模なコラボ企画や,ライバーの方が同時にプレイしやすいゲーム企画が多いのでクラスター係数が高いというのは結構しっくりきます.
4.3 中心性
ここからはネットワーク全体ではなく,個々のノードに着目していきます.個々のノードに対して「中心性」を導出することで,各ノードがネットワーク全体にとって"要"であるかどうかを判断できます.
4.3.1 次数中心性
次数中心性は,各ノードに張られているリンクの数でノードの中心性を測るための指標です.
今回の場合は,「今までコラボした人数が多いほどネットワーク全体にとって重要である」というわかりやすい指標になってます.もっと単純に言ってしまえば「コラボ人数ランキング」ということになります.
# 次数中心性(どれほど多くの人とコラボしているかを測る指標)
deg_C = nx.degree_centrality(H)
# 次数中心性が大きい順にソート
deg_C_list = sorted(deg_C.items(), key=lambda x:x[1], reverse=True)
print(deg_C_list)
結果:
[('椎名唯華', 0.46376811594202894),
('でびでび・でびる', 0.43478260869565216),
('叶', 0.4154589371980676),
('鷹宮リオン', 0.4106280193236715),
('渋谷ハジメ', 0.4106280193236715),
('桜凛月', 0.3864734299516908),
('緑仙', 0.3864734299516908),
('花畑チャイカ', 0.37681159420289856),
('伏見ガク', 0.37681159420289856),
('夜見れな', 0.3719806763285024),
...
4.3.2 近接中心性
次数中心性は,各ノードが他のノードまで平均的にどれくらい近いかを測るための指標です.
今回の場合は,「コラボしたことがない人も含め,他の人との平均的な距離」という指標になっています.具体的な式は,あるノード $i$ から他のノードへの平均距離を $L_{i}$ として,近接中心性 $C_{i}$は
$$
C_{i} = \frac{1}{L_{i}}
$$
で表されます.
# 近接中心性(自分から他人への距離がどれだけ近いかを測る指標)
clo_C = nx.closeness_centrality(H)
clo_C_list = sorted(clo_C.items(), key=lambda x:x[1], reverse=True)
clo_C_list
結果:
[('でびでび・でびる', 0.5001890359168241),
('椎名唯華', 0.49874340286504143),
('アルス・アルマル', 0.49587706146926536),
('渋谷ハジメ', 0.48747236551215917),
('桜凛月', 0.4833759590792839),
('叶', 0.4833759590792839),
('葛葉', 0.4753862738052462),
('剣持刀也', 0.47278141751042285),
('花畑チャイカ', 0.47278141751042285),
('夜見れな', 0.47148966500356376),
...
4.3.3 媒介中心性
次数中心性は,各ノードがネットワークの流れを制御する度合いを測る指標です.
今回の場合は「コラボしたことがないライバー同士の橋渡し役としての重要性」を示す指標になっています.
# 媒介中心性("橋渡し役"としてどれぐらい重要かを測る指標)
bet_C = nx.betweenness_centrality(H)
bet_C_list = sorted(bet_C.items(), key=lambda x:x[1], reverse=True)
bet_C_list
結果:
[('ヌン・ボラ', 0.09566308995092591),
('小野町春香', 0.08902051296783826),
('明楽レイ', 0.06554213546387946),
('ソ・ナギ', 0.061846325534069095),
('イ・ロハ', 0.05134859774139868),
('西園チグサ', 0.0476863865691726),
('椎名唯華', 0.045909796752497574),
('周央サンゴ', 0.03929087934520966),
('ラトナ・プティ', 0.03516799735096999),
('Miyu Ottavia', 0.034613761080624736),
...
4.3.4 固有ベクトル中心性
固有ベクトル中心性は,中心的なノードにつながっているノードも中心が大きという考え方のもと,各ノードの中心性を測る指標です.
# 固有ベクトル中心性(自分がどれだけ"中心"に近いかを測る指標)
eig_C = nx.eigenvector_centrality(H)
eig_C_list = sorted(eig_C.items(), key=lambda x:x[1], reverse=True)
eig_C_list
結果:
[('でびでび・でびる', 0.1477684327754912),
('椎名唯華', 0.14720982804405108),
('鷹宮リオン', 0.14457071842682492),
('渋谷ハジメ', 0.14363375546129273),
('桜凛月', 0.1419820816810376),
('夜見れな', 0.14094732979420704),
('緑仙', 0.1400844559603873),
('叶', 0.1400261470640506),
('アルス・アルマル', 0.13813952769222942),
('不破湊', 0.13720967966477118),
...
5. 中心性の観点からのコラボ関係ネットワークへの簡単な考察
各種中心性から,今回のコラボ関係ネットワークでは「でびでび・でびる」さんと「椎名唯華」さんの二人が,コラボ関係ネットワークで中心的であるという結果が出ました.次数中心性・近接中心性・固有ベクトル中心性の3つの中心性で,お二人ともトップに入っており,他のトップ10の方たちがある程度入れ替わっているところから,今回のネットワークで中心的であるのはこのお二人ということで間違いはないのかなと思います.
また,媒介中心性では,「ヌン・ボラ」さんや「明楽レイ」さんをはじめとした「にじさんじKR」の方が多いことが特徴として出てきています.最近では,FPSゲーム「Apex Legends」でのコラボ配信や大会などで,関わることが多くなってきているので,「にじさんじKR」の方が全体的に媒介中心性が高くなっているのだと思います.さきほどのネットワーク図を見る限り,国境を越えてのコラボはまだまだ少ないなという印象があり,それが媒介中心性にも表れています.
ただし,重要な注意点として,今回のコラボネットワークでは「固有名称が存在するコラボ」しか扱っていません.実際には,今回のネットワーク以上にコラボが行われていることは,考察を深めていくためには考慮しなければならない要素になっていきます.
6. 総括
今回はにじさんじ非公式wikiからスクレイピングしたにじさんじライバーのコラボ関係から作成したネットワークを分析し,どのような特徴を持つのかについて調べました.
このネットワーク図は,とりあえずのデータを突っ込んで作成したものですが,直感的にはわからないこと(誰が一番コラボしているのか?,コラボ関係は全体としてどんな形なのか?)を定量的に評価できる点が非常に良い点であると考えてます.応用可能性としては,
- あるライバーの配信の視聴者に,類似した内容の配信を行うライバーを推薦するシステム
- ネットワークを構築する範囲を広げることで,Vtuber界隈の全体像を把握する
等が挙げられます.ただし,改良点も多く
- 固有名称のあるコラボしか考慮に入れていない
- コラボ回数を考慮していない
等が大きな問題として挙げられます.後者の問題は,「コラボ回数が多いほど結びつきが強くなる」ような「重み付きネットワーク」を導入することで,より深い考察ができるようになりますが,データがまとめられておらず,ネットワークを作成するにはすこし難しいかもしれません.
おわりに
今回初めて記事を書いたので,至らぬところが多々あると思います.記事の中に誤植や,用語についての誤り,質問等があればコメントを頂けると助かります.
また,私事にはなりますが,推しているライバーさんのチャンネルへのリンクを張ることで,記事の締めとさせていただきます.