しっかり学ぶ数理最適化 ヒューリスティック編

これはどんな記事?

本記事は、私がヒューリスティック関連の知識をまとめることになった際に作成したJupyter Notebookを、Qiitaの記事へと改変したものです。

前提としてこれは梅谷俊治先生の「しっかり学ぶ数理最適化 モデルからアルゴリズムまで」という本(以下、教科書と表記)の内容に準拠しています。
そしてその内容の多くは、ありがたいことにネット上の様々な形で公開されており、梅谷先生によるスライド1やスライド2、日本オペレーションズ・リサーチ学会(以下、ORと表記)での記事1や記事2、そしてORの他の方の記事1や記事2などでも類似した内容を見ることが可能です。
(そしてそれ故に、本記事を公開させて頂いています。流石に本家の方がネット上で公開されていない内容を書くのは、例え権利的に問題がないとしても気が引けるので……)

また、この記事は、それらの内容を踏まえた上で、私がネット上の様々な情報をかき集めながら、特に視覚化に焦点をあてて執筆したものになっています。(なので、説明やコードに誤りがあった場合、100%それは私に起因する誤植であることをご承知おき下さい。また、ご指摘等もお待ちしております。)

なお、この本はヒューリスティックの知識のみならず、非常に数多くの数理最適化の知識が詰め込まれた、本当に素晴らしい一冊でした。この本のAmazonへのリンクも感謝の意味を込めて掲載しておきます。また、梅谷先生には、BLF法等のHP上に公開されているプログラムの一部使用も許可して頂きました。改めてお礼申し上げます。

章	扱う内容
複雑な関数の最適化	局所探索法、多スタート局所探索法、反復局所探索法、可変近傍探索法
巡回セールスマン問題	2-opt、bitdp、タブーサーチ、誘導局所探索法
円詰め込み問題	焼き鈍し法、山登り法、大洪水法、閾値受理法
長方形詰め込み問題	BLF法、探索空間について
MountainCar	遺伝的アルゴリズム、局所探索法

では、以下からNotebookの内容です。

はじめに

本ノートブックでは、 発見的解法(heuristics) について、扱います。

ちなみに、ヒューリスティックという単語に聞き慣れない方もいるかと思うので、簡単にIoT用語辞書から定義を引っ張ってくると、

ヒューリスティック、またはヒュリスティック（ヒューリスティックス、ヒュリスティックス[heuristics]とも）とは、ある程度正解に近い解を見つけ出すための経験則や発見方法のことで、「発見法」とも呼ばれます。
いつも正解するとは限らないが、おおむね正解するという直感的な思考方法で、たとえば、服装からその人の性格や職業を判断するといったことは、ヒューリステックな方法といえます。理論的に正しい解を求め、コンピュータのプログラムなどに活用される「アルゴリズム」に対置する概念です。

と言う風になっています。

教科書における対応範囲は、大まかには4.6, 4.7節に相当します。
なお、都合上教科書とは順番を少し変えて各内容を見ていくことにします。また、教科書に載っている内容の全ては、本ノートブックには載っておらず、逆もまた然りです。

前準備

以下から出てくるコードは全て、実行環境としてGoogle Colabを想定しています。

!pip install gym pyvirtualdisplay > /dev/null 2>&1
!apt-get install -y xvfb python-opengl ffmpeg > /dev/null 2>&1
!apt-get update > /dev/null 2>&1
!apt-get install cmake > /dev/null 2>&1
!pip install gym[atari] > /dev/null 2>&1

import io
import os
import gym
import math
import time
import glob
import base64
import random
import datetime
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import matplotlib.animation as animation
from typing import List,Tuple 
from matplotlib import gridspec
from gym.wrappers import Monitor
from pyvirtualdisplay import Display
from matplotlib.colors import ListedColormap
from IPython import display as ipythondisplay
from IPython.display import HTML,display,YouTubeVideo
%matplotlib inline

本編

複雑な関数の最適化

初めに、ヒューリスティックの最も基本的な戦略である局所探索法についてみていきます。

説明

簡単に局所探索法に関する説明をします。

数理計画用語集によると、局所探索法とは、

「適当な初期解から出発し，解の近傍にそれより良い解があれば置き換える，という操作を繰り返し実行して，解の更新が行われなくなったとき終了する」というアルゴリズム

とされています。非常にシンプルかつ基本的な考え方なので、多くの手法がこれに当てはまっています。

[用語]

• 初期解
  初期の解(そのまんま)
  とりあえずは(場合によっては実行不能領域内の解であっても)何か一つ解を取ってきているものと思ってもらえれば大丈夫かと思われます。一般には何か別のアルゴリズム(貪欲法など)でそこそこ良い解を適当に取ってきていることも多いように感じています。

• 近傍
  今持っている解に少しの変更を加えることによって得られる解の集合のこと。
  「近傍が大きい」「近傍が小さい」という表現もありますが、これは「ある解と別の解(近傍内の解)がどれだけ似ているか」ということを言っているとも捉えられます。
  「良い解どうしは似た構造を持つ」という近傍最適性(proximity optimality principle, POP)が、この近傍というものを考える妥当性になっています。

• POP
  先述の通り、POPは近傍最適性という意味です。一見このPOPは当たり前の性質にも見えます。
  例えば、家から駅までの一番短い経路と、二番目に短い経路では、大部分が同じ経路で、違う部分はわずかなはずです。このような場合は、確かに、「良い解どうしは似た構造を持つ」と言えるでしょう。
  しかし、このPOPが成り立たない例もあります。例えば、前回の宝くじでは「123456」番が当選番号だったからと言って、今回の宝くじの当選番号はそれに近い数字、つまり「15234_6」(5を2の位置に挿入した番号)や「153426」(5と2を交換した番号)であるかと言えば、当然ながら全くそうではありません。つまり、局所探索法は使えません。
  しかし、POPが成立すれば、これらは妥当な解の一つとなりえます。
  なお、前者のことを挿入近傍、後者のことを交換近傍とも言います。(以下の図は局所探索法とその拡張—タブー探索法を中心としてという記事から引用しました)

• 実行可能解
  制約を満たしている解。線形計画問題などにおいても出てくる用語です。
  探索空間というのは、この実行可能解全体の集合とも言えます。

[手法]
局所探索法という分類には、以下の手法などが該当します。

• 山登り法 (←今扱う手法)
• 焼きなまし法 (以下の三つは後で登場します)
• タブーサーチ
• (遺伝的アルゴリズム) ※注

※注
遺伝的アルゴリズムは、wikiによると狭義には局所探索法ではないらしいです。
ただ、数理計画用語集によると広義には局所探索法らしいです。

実践

ここでは、局所探索法のイメージを掴みながら、具体例として以下の関数$f(x)$を最小化していきます。
私が適当に計算して設定した関数です。
実行可能領域は、グラフ描画の便宜上、$-3.3 \leq x \leq 3.3$としました。

(なお、これはあくまで例であるため、複雑な関数の最適化が絶対に局所探索法を用いて行われている、という訳では全くないことに注意してください。)

def f(x):
    x=np.clip(x,-3.3,3.3)
    # (x-3)(7x-13)(3x-4)(x+3)(2x+5)(x+1) + C
    return (+44*(x**6) + 13*(x**5) - 638*(x**4)
            -88*(x**3) + 2600*(x**2) - 261*x + 6.5653624787847)

まずは特に工夫をせずに、局所探索法を使用して、最適化を試みます。

局所探索法の具体的な手順は以下の通りです。

局所探索法(教科書p.284からの引用)

Step1. 初期解 $ x^{(0)} $ を定める。 $ k=0 $ とする。
Step2. 近傍 $ N(x^{(k)}) $ 内に $ f(x')<f(x) $ となる改善解 $ x' $ がなければ終了。
Step3. 改善解 $ x' \in N(x^{(k)}) $ を1つ選んで、 $ x^{(k+1)}=x' $ とする。 $ k=k+1 $ としてStep2に戻る。

改善解があればそれを必ず採用するという、極めてシンプルな手法ですね。wikiにも擬似コードが掲載されています。
なお、この手順のことを山登り法とも言います。

また、以下にその局所探索法を使用したコードを載せています。コメントも読めば、Pythonを知らない方でも、ざっくりとイメージはつかめるでしょうか。なお、コード中には「見る必要なし」や「ここが重要」という文言がありますが、関数ごとに重要度が異なっていますので、そのような緩急をつけて読んで頂くのが一番分かりやすいかと思われます。

def vis(hists: List[List[float]], draw_arrow: bool = False) -> None:
    """ビジュアライズ用関数 見る必要なし

    Args:
        hists (List[List[float]]): 表示する探索履歴のリスト 途中は5個ずつ間引いて表示する
        draw_arrow (bool, optional): 探索履歴同士の遷移を描くかどうか デフォルト値はFalse
    """
    xs = np.linspace(-3.3, 3.3, 100)
    ys = f(xs)
    fig = plt.figure(figsize=(12, 5))
    ax = fig.add_subplot(111)
    ax.plot(ys)
    ax.set_title("f(x) (-3.3 <= x <= 3.3)")
    ax.set_xlabel("x")
    ax.set_ylabel("f(x)")
    ax.set_xticks(np.linspace(0, 100, 5))
    ax.set_xticklabels([-3.3, -1.65, 0, 1.65, 3.3])
    ax.grid()
    for hist in hists:
        for i in range(1, len(hist)-1, 5):
            ax.plot((hist[i]+3.3)/6.6*99,
                    f(hist[i]), 'o', color="gray")
        ax.plot((hist[0]+3.3)/6.6*99,
                f(hist[0]), 'o', color="blue")
        ax.plot((hist[-1]+3.3)/6.6*99,
                f(hist[-1]), 'o', color="red")
    if draw_arrow:
        for i in range(len(hists)-1):
            ax.annotate("", xytext=((hists[i][-1]+3.3)/6.6*100, f(hists[i][-1])),
                        xy=((hists[i+1][0]+3.3)/6.6*100, f(hists[i+1][0])),
                        arrowprops=dict(arrowstyle="->",
                                        color="green"))
    plt.show()


def local_search(x0: int) -> List[float]:
    """局所探索法

    Args:
        x0 (int): 初期解

    Returns:
        List[float]: 探索履歴
    """
    x0 = np.clip(x0, -3.3, 3.3)
    x = x0             # 適当な初期解
    k = 0              # 探索回数
    best_score = f(x)  # 目的関数の値
    hist = [x]         # 解の履歴

    # ここが重要!
    while k < 100:     # 探索回数の上限
        k += 1
        Nx = np.linspace(x-0.05, x+0.05, 10)  # 解xの近傍
        fNx = f(Nx)                           # 近傍の各点における目的関数の値
        if np.any(fNx < best_score):  # 近傍に今より良い解があった場合、それを採用
            new_x = np.random.choice(Nx[np.where(fNx < best_score)[0]])
            best_score = f(new_x)
            x = new_x
            hist.append(new_x)
        else:                         # 近傍に今より良い解がなかった場合、探索を終了
            break

    assert(len(hist) == k)
    print(f"探索回数: {len(hist)}回")
    print(f"得られた最適値: {f(hist[len(hist) - 1])}")
    print("真の最適値: 0")
    return hist

以上で定義した関数を、実行してみます。

hist = local_search(x0=-2)  # -2は適当な初期解
vis([hist])

実行結果

探索回数: 26回
得られた最適値: 2666.7852665513115
真の最適値: 0

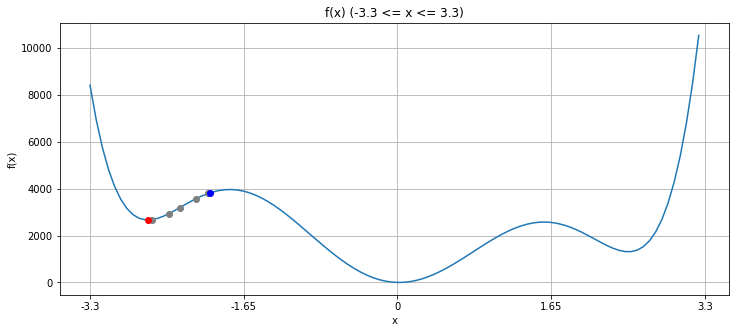
青が初期解、±0.05の範囲を近傍として、その近傍内で最も目的関数の値が小さくなる灰色の点を経由しながら最適化していき、最終的に赤が求まった解、という風になっています。
ここで、今考えている問題の目標は、関数$f(x)$の最小化であったことを思い出して下さい。つまり、このグラフの一番窪んでいる部分である、$f(x)=0$に到達することを目指しています。

局所探索法の改良

さて、先程の項で出力されたグラフを見れば、確かに初期解よりも良い解を得られているものの、今得られている解は局所最適解(locally optimal solution)になってしまっていることが分かると思います。(局所最適に陥るとも言います。)

局所最適解であるとは、即ち、今の解の近傍にそれより良い解が存在しないということを意味しています。
ネット上である方はこのことを指して「地元では負け知らず」と表現されていましたが、個人的には非常に好きな言い回しです。
ここで本当に欲しいのは「全国で負け知らず」な解なので、何とかする必要があります。

これを解決するには様々な方法が知られていますが、ここでは局所探索法の自然な拡張とも言える、多スタート局所探索法と反復局所探索法、そして可変近傍探索法についてみていきます。

多スタート局所探索法

競技プログラミング(以下、競プロと表記)的な文脈では、よく多点スタートとも呼ばれます。
ほぼ名前通りの内容ですが、多くの初期点からスタートして、一番良い局所最適解を最良の解とするだけです。誤解を恐れずに言えば、「全国で負け知らずな子が欲しいなら、様々な市区町村から地元で負け知らずの子を集めて比べればいい」という考え方です。

(競プロ的補足 AHC002というコンテストにおけるtourist(競プロ界の王様)の解は多点スタート(的な)解法でした。より厳密には、ある要素を24通り全探索して、その結果からいいものを5個選び(ここが多点スタート)、その各初期点に対して適切な近傍によって山登りし、最後にSA(simulated annealing)をして解を求めていました。このように、多点スタート+何か別の手法とすることも多くあります。)

これは tourist の提出#AHC002https://t.co/75ARFHGF8W pic.twitter.com/k4c64P79Is

— kimiyuki@うさぎ🐇 (@kimiyuki_u) April 28, 2021

なお、この方針は初期値依存性が高い時に特に有効に働くと、一般に言われています。
例えばですが、先程使用した$f(x)$よりも遥かにギザギザした関数を考えてみます。このような場合は、近傍を探索するということがあまり有効に働かず、寧ろ宝くじに近い状況になっています。宝くじは当然購入枚数が多ければ多いほど一等を引ける確率は上がるので、多スタート局所探索法の有効性が分かるかと思います。

それではこの考え方も取り入れて局所探索をしてみます。

def multi_start_local_search() -> None:
    """多スタート局所探索法"""
    hists = []
    # 多スタートにも色々流儀はありますが、ここではランダム多スタート局所探索法を用います
    for _ in range(5):
        print("-"*20)
        x0 = random.uniform(-3, 3)  # ランダムに初期解を生成し、
        hist = local_search(x0)     # その初期解に対して局所探索することを繰り返す
        hists.append(hist)
    vis(hists)

multi_start_local_search()

実行結果

--------------------
探索回数: 68回
得られた最適値: 0.003976363767456803
真の最適値: 0
--------------------
探索回数: 48回
得られた最適値: 0.0003761922566711817
真の最適値: 0
--------------------
探索回数: 15回
得られた最適値: 1310.0859051457142
真の最適値: 0
--------------------
探索回数: 9回
得られた最適値: 2666.8270888162524
真の最適値: 0
--------------------
探索回数: 14回
得られた最適値: 0.000287468676853031
真の最適値: 0

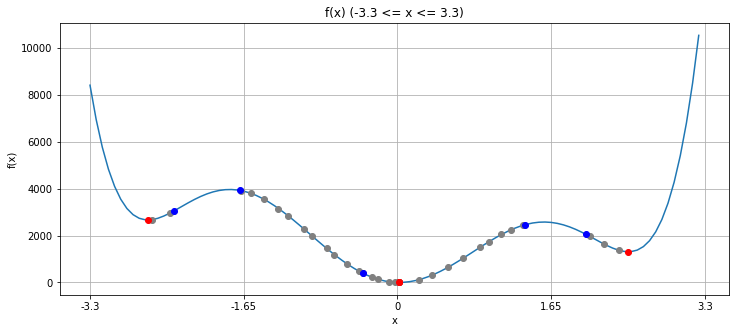
この手法はランダム性があるので必ずしも大域最適解が得られるとは限りません。しかし、今回は5個選んだ初期点の内、2つは大域最適解でない解になっているものの、3つはきちんと大域最適解の0になっています。

反復局所探索法

続いてみていくのは、反復局所探索法です。
これは、局所探索法で得られた暫定解に対して、ランダムな変形を加え、それを新たな初期点として反復的に探索していく手法になっています。過去の探索履歴を利用している点が特徴的とも言えるでしょう。
競プロ文脈ではキックと呼ばれる操作に近いかもしれません。(用語の定義が曖昧なので、厳密には少し違うかも知れませんが、以下ではこの用語を使います。)
そして、これまた誤解を恐れずに言えば、「地元では負け知らずな子に対して、伸び悩む時期が来てしまったら、これまでと違う練習方法などを取り入れて更なる成長を促し、全国で負け知らずを目指していく」と言った感じでしょうか。

def iterated_local_search(x0: int) -> None:
    """反復局所探索法

    Args:
        x0 (int): 初期解
    """
    hists = []
    for _ in range(5):
        print("-"*20)
        xnatural = x0              # 暫定解
        hist = local_search(x0)    # 今持っている初期解に対して局所探索をする
        hists.append(hist)
        xdash = hist[-1]           # その局所探索で得られた局所最適解
        if f(xdash) < f(xnatural): # 新たな解の方が良い場合、暫定解を更新する
            xnatural = xdash
        x0 = xnatural+random.uniform(-1.5, 1.5)  # 今までの最良解にランダムな変形を加える キック
    vis(hists, draw_arrow=True)

iterated_local_search(-2)

実行結果

--------------------
探索回数: 26回
得られた最適値: 2666.7852665513115
真の最適値: 0
--------------------
探索回数: 47回
得られた最適値: 0.0010018435198233533
真の最適値: 0
--------------------
探索回数: 20回
得られた最適値: 0.0008274340568759087
真の最適値: 0
--------------------
探索回数: 17回
得られた最適値: 0.015188443098042015
真の最適値: 0
--------------------
探索回数: 5回
得られた最適値: 0.012423503853643325
真の最適値: 0

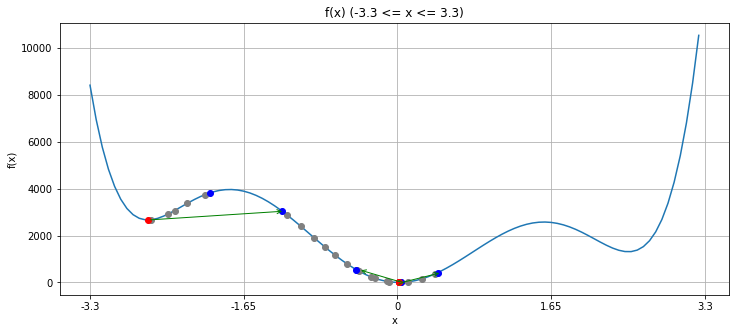
少し見づらいですが、緑の矢印がキックによる遷移を表しています。
青から赤へ局所探索法で移動し、赤から青へキックによって遷移する、というのを、確かに「反復」しているということが伝わるでしょうか。
これもまたランダム性があるので必ずしも大域最適解が得られるとは限りませんが、左側にある局所最適解から、運よく真ん中の大域最適解へとつながる初期点に移ることが出来たので、目標を達成できています。

この方針において大切になる要素の一つは、局所探索で得られた暫定解にどのようにして変更を加えるかです。キックに相当する操作と、近傍を得る操作が似ていることは、一般に望ましくありません。似たような遷移ばかりを繰り返していると、同じような解しか得られないからです。
(今は問題が非常にシンプルな為、ほぼ同じ操作を、仕方なくしていますが。)

なので、「局所探索で使う近傍」と「キックで使う近傍」を区別するということが重要です。教科書では、この二つの近傍の例としてTSPの2-optとdouble-bridgeが挙げられています。(TSPについては後程扱います)

可変近傍探索法

さて、次に見ていくのは可変近傍探索です。
この探索方法では、キックで使う近傍の大きさを適応的に変化させていることが特徴となっています。
これまた誤解を恐れずに言えば、「伸び悩み時期の新たな練習方法として、どういったものが最善かはよく分からないから、とりあえず段々と負荷を高めていって様子を見てみよう」という考え方でしょうか?

def variable_neighborhood_search(x0: int) -> None:
    """可変近傍探索法

    Args:
        x0 (int): 初期解
    """
    xnatural = x0  # 暫定解
    hists = []     # 探索履歴
    k = 0          # 可変近傍のパラメータ
    for _ in range(5):
        print("-"*20)
        hist = local_search(x0)  # 今持っている初期解に対して局所探索をする
        hists.append(hist)
        xdash = hist[-1]         # その局所探索で得られた局所最適解
        if f(xdash)+0.05 < f(xnatural):  # 暫定解よりも(誤差以上に)良い解が得られれば、
            xnatural = xdash             #   解を更新して、
            k = 1                        #   近傍のサイズを元に戻す
        else:                            # そうでなければ、
            k += 1                       #   近傍をより大きくする
        x0 = xnatural+random.uniform(-2*k, 2*k)  # 近傍のサイズに応じた初期解を生成
        print(f"k = {k}")

    vis(hists, draw_arrow=True)

variable_neighborhood_search(-2)

実行結果

--------------------
探索回数: 30回
得られた最適値: 2666.7852665513115
真の最適値: 0
k = 1
--------------------
探索回数: 26回
得られた最適値: 2666.785266551309
真の最適値: 0
k = 2
--------------------
探索回数: 54回
得られた最適値: 0.002529135259733195
真の最適値: 0
k = 1
--------------------
探索回数: 26回
得られた最適値: 0.0029800005352429437
真の最適値: 0
k = 2
--------------------
探索回数: 29回
得られた最適値: 1310.097308813496
真の最適値: 0
k = 3

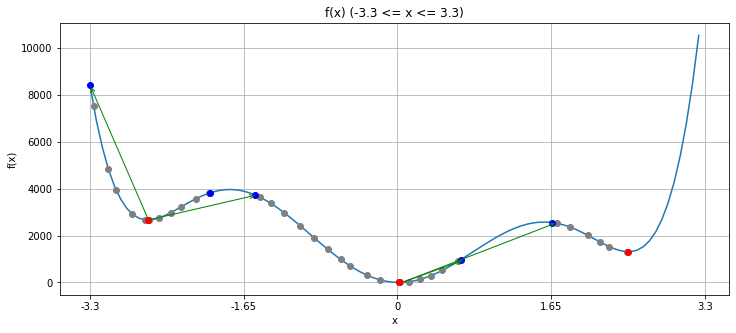
これまたランダム性があるので必ずしも大域最適解が得られるとは限りませんが、先程よりも大域最適解が得られる可能性は高い(はず)です。
左の局所最適解にまず嵌った後、キックの近傍を大きくすることで真ん中の大域最適解に移ります。そしてこの点が本当に大域最適解かどうかは、グラフの真の形を知らない場合は分からないので、再びキックの近傍を大きくしていき、右の局所最適解へと通じる初期点を得ます。しかし、実際にはその局所最適解は真ん中の解よりも悪い解なので、結局真ん中の局所最適解(=大域最適解)を答えとして出力します。と、言ったことが行われています。

更なる局所探索法について

グラフを用いて説明するのは以上になりますが、局所探索法についての話題はこれだけに留まりません。

例えば、tsukammoさんによるこの記事は局所探索法についての記事ではありませんが、局所探索法において重要な、近傍の取り方の工夫、そしてスコア関数の計算の高速化、差分化などについても取り上げられています。ちなみに私がヒューリスティックを学び始めるきっかけにもなった記事でもあります。
こういった素晴らしい記事等も合わせてご覧いただくのが、局所探索法を更に学ぶには一番良さそうです。

また、一つ書こうとして(ここでは)書けなかった手法があるのですが、それが誘導局所探索法(Guided Local Search,GLS)です。

この手法に関して、非常にざっくりとした説明だけすると、「局所最適解という窪みを埋めてくれるペナルティ関数を持ってきて、その局所最適解から脱出し、真の大域最適解を目指す」といったような手法です。

参考資料が乏しく、具体的にどうすればいいのかというところまでは確信を持てなかったというのが、ここで扱えない主な理由です。(適当なペナルティでよしなにやることは可能かもしれませんが、あまり適当なことは書きたくないので……。何か分かれば追記をしようと思います。)

なお、Twitterでは梅谷先生のこんな発言もありました。

個人的な経験では，アニーリング法やタブー探索法など改悪解への移動を許容する戦略よりも，誘導局所探索法などの評価関数を変形させる戦略の方が効果的かなと思ってる．あちらこちらと動き回って高い山を乗り越えるよりも，高い山を低くした方が乗り越えるのは簡単なので・・・

— Umepon (@shunji_umetani) January 13, 2020

(※アニーリング法とタブー探索法は後述します。)

個人的な知名度の感覚としては、誘導局所探索法の方が，アニーリング法やタブー探索法などに比べて、圧倒的に低いと思っていたので、このような評価を下されているのは正直意外でした。

また、教科書では誘導局所探索法の応用例として、TSPに関するもの(これは後程扱います)が紹介されていますが、他にも配送計画問題などで応用できるそうです。

• 参考資料
• https://en.wikipedia.org/wiki/Guided_Local_Search (wiki)
• http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=79D883C1455A0D775D781C658F770C2C?doi=10.1.1.170.689&rep=rep1&type=pdf
  (Voudouris, C. (1998). Guided Local Search—An illustrative example in function optimisation. BT Technology Journal, 16(3), 46-50.
  $ F6(x,y)=0.5+\frac{\sin^2{\sqrt{x^2+y^2}}-0.5}{(1.0+0.001(x^2+y^2))^2} $ という関数をGLSで解いた論文)
• https://slideplayer.com/slide/14171683/ (ウォータールー大学の講義資料 これの20頁以降の図が分かりやすいです。)

局所探索法のまとめ

以上、局所探索法について紹介しました。

ここで紹介した手法は、どれも非常に普遍的な考え方であることも注目に値する事実です。 目的関数やコードの具体的内容に関わらず、様々な手法、様々な場面で使える考え方となっています。 このように「特定の計算問題に依存しないヒューリスティクス」のことをメタヒューリスティックと呼びます。

局所探索法には他にも様々なメタヒューリスティックが存在し、そしてそれがメタ的であるが故に他の探索手法にも応用可能な点が、個人的には面白い点の一つだなと思っています。

巡回セールスマン問題

続いて、この項では、巡回セールスマン問題（TSP）について扱います。

説明

TSPのwikiによる定義は、

巡回セールスマン問題（じゅんかいセールスマンもんだい、英: traveling salesman problem、TSP）は、都市の集合と各2都市間の移動コスト（たとえば距離）が与えられたとき、全ての都市をちょうど一度ずつ巡り出発地に戻る巡回路のうちで総移動コストが最小のものを求める（セールスマンが所定の複数の都市を1回だけ巡回する場合の最短経路を求める）組合せ最適化問題である。

となっています。

これはNP困難問題の中で、最も有名な問題であると言っても過言ではない程に、よく知られた問題です。

また、TSPは名前からセールスマンに対してしか役に立たない問題なのでは? と思ってしまうかも知れませんが、他にも応用例は多数あります。
例えば、梅谷先生のスライドでは「配送計画，基盤穿孔，鋼板の圧延計画など」の、応用例が紹介されています。
他にも、ドリル穴あけ計画問題という問題もどうやらあるらしく、電子基盤に穴をあける（部品を埋め込む）順序を決定する問題にも、TSPが使えるそうです。

実際、つい最近開催されたAsprova社による生産スケジューリング問題に関するコンテストでも、TSPを使用した参加者(私)はいました。生産スケジューリング問題でもTSPが使えるというのは、よくよく考えると少し驚きかも知れません。

さて、説明はこのくらいにして、以下から実際にTSPを解いていきます。
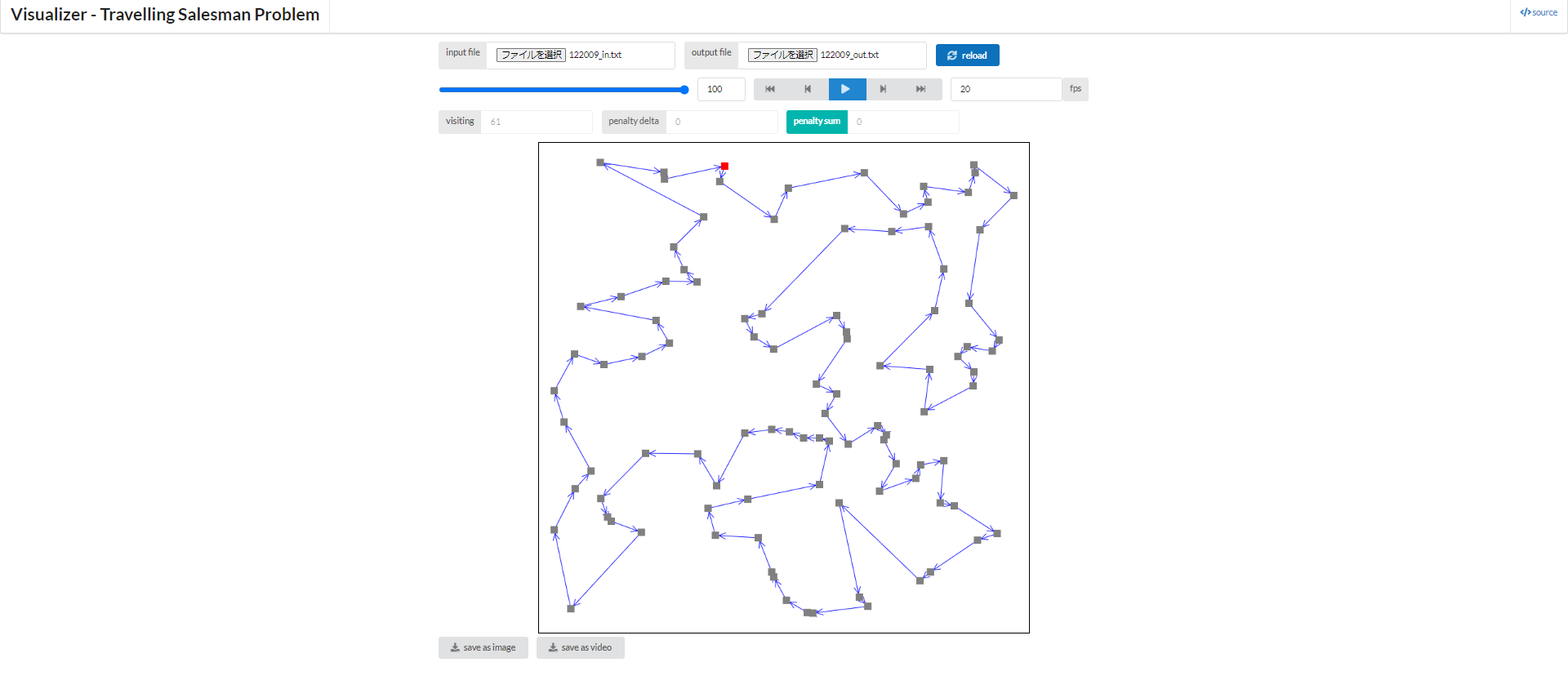
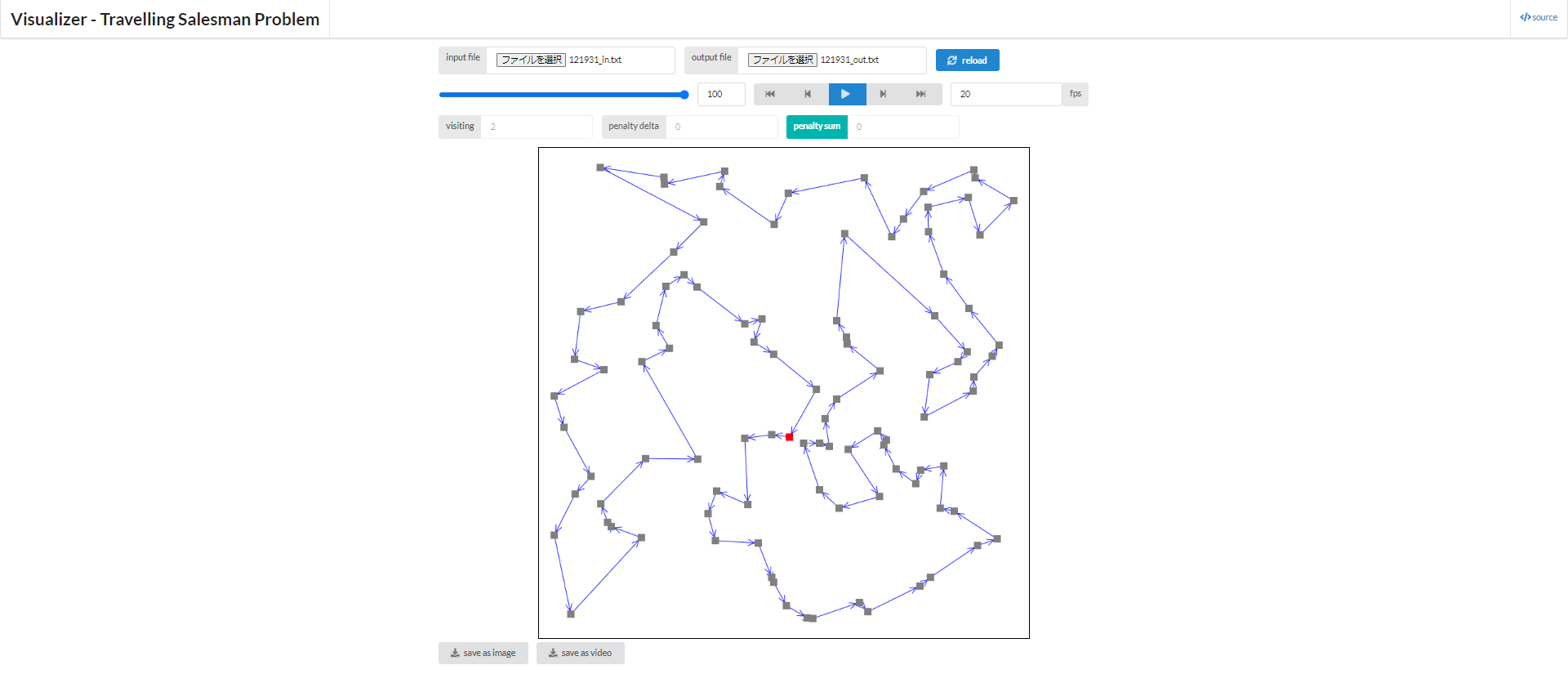
ここでは、このリンクから利用できるビジュアライザを利用して、その概略を掴むことを目的とします。(このビジュアライザのGitHubのページ)

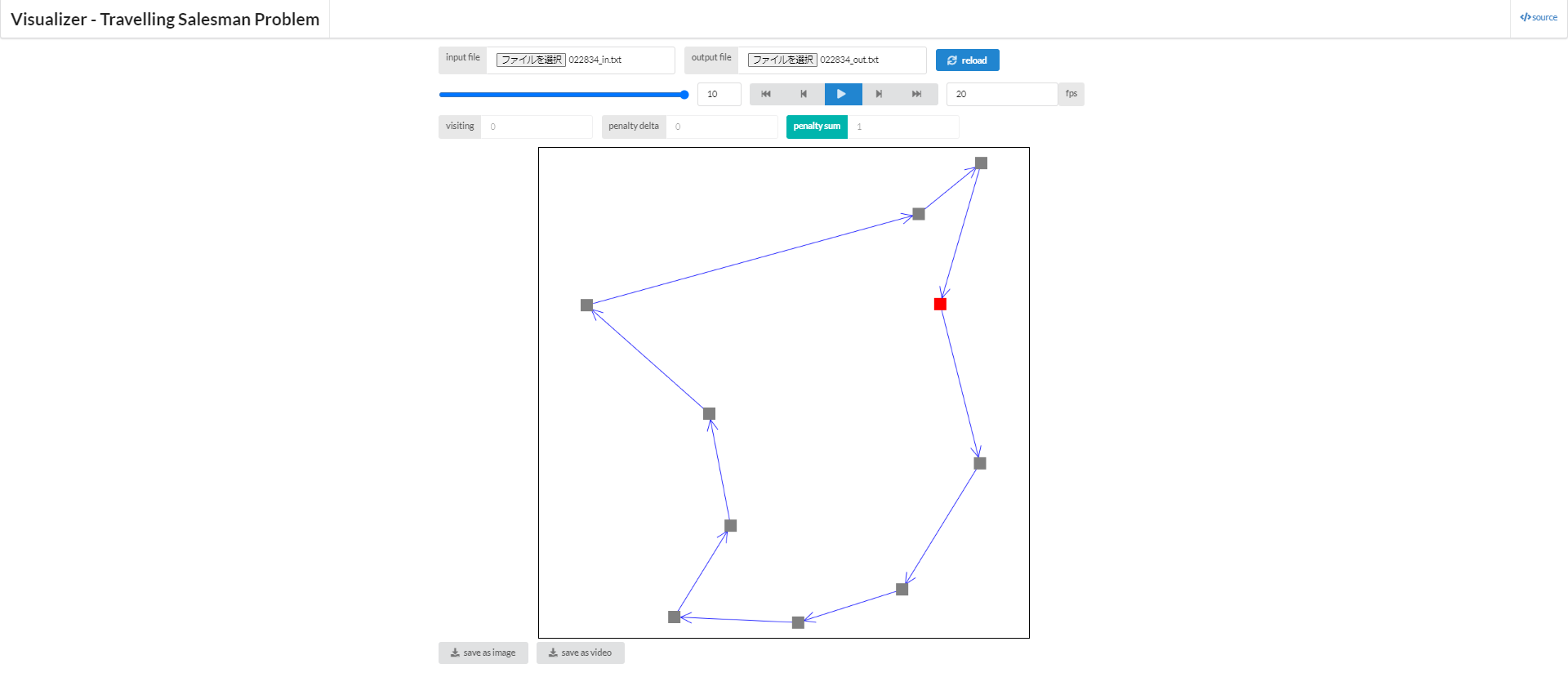
TSPをそもそもご存じでない方は、上の図を見ると分かりやすいと思います。リンク先のビジュアライザを使用した画像です。各点がそれぞれ都市に対応していて、赤の点から出発し、全ての点をちょうど一度ずつ巡り、再び元に戻ってくる、そしてその経路長を最小化したい。これがTSPの扱う問題となります。

実践

では、TSPについて解いていきます。
まず、いくつかの関数を定義します。これら非本質的部分なので、読む必要性は全くありません。

def dist(xy1: Tuple[int, int], xy2: Tuple[int, int]):
    """2点間の距離を返す math.distの代用"""
    return math.sqrt(abs(xy1[0]-xy2[0]) ** 2 + abs(xy1[1]-xy2[1]) ** 2)


def calc_total_dist(adj: List[List[float]], tsp_route: List[int]) -> float:
    """ある道順に沿って移動した際の総移動距離を計算する

    Args:
        adj (List[List[float]]): 隣接行列
        tsp_route (List[int]): 各都市の訪問順序を表す順列

    Returns:
        float: 総移動距離
    """
    ret = adj[tsp_route[len(adj) - 1]][tsp_route[0]]
    for i in range(len(adj) - 1):
        ret += adj[tsp_route[i]][tsp_route[i + 1]]
    return ret


def make_problem(N: int = 10, seed: int = 0):
    """TSPの問題を作成する

    Args:
        N (int, optional): 都市数 デフォルト値は10
        seed (int, optional): 乱数のシード デフォルト値は0

    Returns:
        以下の二つのTuple
        cities (List[Tuple[float,float]]): 各都市のxy座標を記したリスト
        adj (List[List[float]]): 隣接行列 つまり、adj[x][y]がxy間の距離
    """
    random.seed(seed)
    cities = [(random.random(), random.random()) for _ in range(N)]
    adj = [[dist(cities[i], cities[j]) for j in range(N)]
           for i in range(N)]
    return cities, adj


def bitdp(adj: List[List[float]]):
    """bitDP (アルゴ、厳密)
    本ノートブックはヒューリスティックに焦点を当てているので詳しくは触れませんが、
    例えば以下のサイトを見るとやっていることがつかめると思います
    https://algo-logic.info/bit-dp/

    計算量 O(N^2 2^N)


    Args:
        adj (List[List[float]]): 隣接行列 -1の時、通行不可であることを示す

    Returns:
        以下の二つのTuple
        ans (float): 総移動距離
        route (List[int]): 各都市の訪問順序を表す順列
    """
    N = len(adj)  # 都市数
    assert N <= 10, "bitDPで解く問題のサイズは小さくないといけません"
    assert 1 <= N and N == len(adj[0]), "隣接行列ではありません"
    dp = [[1e9+7 for _ in range(N)] for _ in range(1 << N)]
    for i in range(N):
        dp[1 << i][i] = adj[0][i]
    for bit in range(1, 1 << N):
        for v in range(N):
            if not bit & (1 << v):
                continue
            for nv in range(N):
                if bit & (1 << nv) or adj[v][nv] == -1:
                    continue
                dp[bit | (1 << nv)][nv] = min(dp[bit | (1 << nv)][nv],
                                              dp[bit][v] + adj[v][nv])
    ans = dp[(1 << N) - 1][0]
    # 以下復元をします。 ちょっとこのやり方は怪しいかも(自己流)
    now = 0
    route = [now]
    visited_bit = (1 << N) - 1
    dist_sum = ans
    EPS = 1e-5
    for _ in range(N-1):
        visited_bit ^= (1 << now)
        for last_city in range(N):
            if last_city == now:
                continue
            if abs(dist_sum - dp[visited_bit][last_city]
                   - adj[last_city][now]) < EPS:
                break
        else:
            assert(False)
        dist_sum -= adj[last_city][now]
        now = last_city
        route.append(now)
    return ans, route


def make_vis_data(cities: List[Tuple[float, float]], tsp_route: List[int]) -> str:
    """ビジュアライズ用関数

    Args:
        cities (List[Tuple[float,float]]): 各都市のxy座標を記したリスト
        tsp_route (List[int]): 各都市の訪問順序を表す順列

    Returns:
        data_id (str): 作成したデータのtxtファイルを表すための数字列
    """
    dt = datetime.datetime.now()
    data_id = f"{dt.hour:02}{dt.minute:02}{dt.second:02}"
    if not os.path.exists("tsp_vis_data"):
        os.mkdir("tsp_vis_data")
    with open(f"tsp_vis_data/{data_id}_in.txt", mode='w') as f:
        f.write(str(len(cities)))
        f.write("\n")
        for x, y in cities:
            f.write(str(x) + " " + str(y) + "\n")
    with open(f"tsp_vis_data/{data_id}_out.txt", mode='w') as f:
        f.write(' '.join([str(v) for v in tsp_route]))
        f.write("\n")
    print("作成したデータ: ", end="")
    print(f"tsp_vis_data/{data_id}_in.txt, tsp_vis_data/{data_id}_out.txt")
    return data_id

解法1 bitdp

早速上で定義した関数を使用して、都市の数が10の場合についてみていきます。
これほどまでに都市の数が少ないと、bitdpと呼ばれるアルゴリズムで厳密に解くことが出来るので、まずはその解法による解を見てみます。
コード中のコメントにも書きましたが、このアルゴリズムについてあまり深くは触れません。詳しく知りたい方は、アルゴリズムロジックというサイトによるbitdpの解説などを参照して下さい。

cities, adj = make_problem(N=10) # 適当に問題を作成し、
ans, route = bitdp(adj)          # bitdpで厳密に解く。
print("総移動距離: ", ans)
print("訪問順序: ", route)
data_id = make_vis_data(cities, route) # そしてビジュアライザ用のデータを生成

print("\nデータ内容の確認")
!cat "tsp_vis_data/{data_id}_out.txt"

実行結果

総移動距離:  2.3937246803810788
訪問順序:  [0, 5, 3, 7, 1, 2, 4, 6, 9, 8]
作成したデータ: tsp_vis_data/022834_in.txt, tsp_vis_data/022834_out.txt

データ内容の確認
0 5 3 7 1 2 4 6 9 8

Google Colabでこのコードを走らせる場合の補足

上のセルを実行すると、問題とその解が記されたtxtファイルが作成されます。作成したデータは、Google Colab上に保存されています。

表示環境によっては違うかも知れませんが、画面左側にフォルダのマークがあるかと思います。
そこをクリックして、「tsp_vis_data」、とフォルダがあると思うので、それを更にクリックすれば、上のセルの実行結果にあるファイルが存在していると思います。もし、より上位の階層に行ってしまった場合は「content」というフォルダを見れば大丈夫です。

そしてそれらをダウンロードして、先程も紹介したサイトに突っ込めば、ビジュアライズされると思います。

もし上手くいかなければ、添付してある画像だけで楽しんでもらえれば。
(補足終わり)

bitdpの解は、先程掲載させて頂いた画像が正しくそれになっています。実際、最も総移動距離が短いと思われる経路を提示してくれています。

解法2 2-opt

さて、先程はbitdpでTSPを厳密に解きましたが、これの計算量は $ O(2^n n^2) $ です。

この計算量はかなり爆発的です。どのくらいのものなのかを確認するために、$ n=100 $ を代入してみます。

\begin{align}
 2^n n^2 &\simeq 1.2676506 \times 10^{34} \\
         &\simeq 10^7 \times 31536000 \times 4.0196937 \times 10^{19}
\end{align}

ここで、$10^7$は一秒間にコンピューターが処理できる大体の数、31536000は一年の大体の秒数になっているので、この計算にはざっと4000京年程かかるということを示す結果になっています。

長さ100の順列の通り数は約$9.332622 \times 10^{157}$なので、かなり効率的ではありますが……。

こういった事情があることも踏まえると、10秒かそこらでも十分に妥当な解を出力できるヒューリスティック的解法の重要性は伝わりやすいのではないでしょうか。

以上でヒューリスティックをする動機を大まかに理解してもらえたと思うので、具体的手法について踏み込んでいきます。
TSPには教科書に記載があるものも含め非常に数多くの発見的解法がありますが、ここでは2-optと呼ばれる手法を扱います。

実装は以下の記事を一部参考にさせて頂いています。

2-optとは?
wikiを見るのが分かりやすそうです。以下の図もwikiからの引用です。
この図をじっと眺めると、上の図では 「b→e→…→c→f」 という順番で訪れていますが、これをswapするような形で、下の図のように 「b→c→…→e→f」 と訪れることも可能であり、実際こちらの方が経路が短くなっています。
まさにこの入れ替え操作こそが、2-opt近傍操作になっています。
なお、上の説明の「…」にあたる部分は、順番がひっくり返されている事に注意してください。

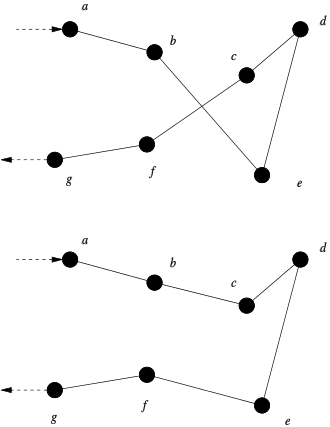
そして、この2-opt近傍操作を試し、実際に経路長が短くなっていればその操作を採用する、ということを繰り返すことによって、適当な初期解から出発して、妥当な解を得ようとするのが、2-opt法になっています。

def two_opt(adj: List[List[float]], TL: float = 2.0):
    """two_opt (ヒューリスティック、非厳密)

    Args:
        adj (List[List[float]]): 隣接行列
        TL (float, optional): 実行制限時間 デフォルト値は2.0

    Returns:
        以下の二つのTuple
        ans (float): 総移動距離
        route (List[int]): 各都市の訪問順序を表す順列
    """
    N = len(adj)  # 都市数
    assert 1 <= N and N == len(adj[0]), "隣接行列ではありません"
    route = [i for i in range(N)]  # 訪問順序の初期解
    loop_cnt = 0
    start_time = time.perf_counter()

    # ここが重要!
    while time.perf_counter() - start_time < TL:  # 制限時間になるまで以下のコードを回す
        loop_cnt += 1
        # 適当に4点a,b,c,dを取ってくる。
        a = random.randrange(N - 1)
        b = random.randrange(N - 1)
        if a == b:
            continue
        if a > b:
            a, b = b, a
        d = (a + 1) % N
        c = (b + 1) % N
        # ここのif文が2-opt法の本質的部分!
        if (adj[route[a]][route[b]] + adj[route[c]][route[d]] <=
                adj[route[a]][route[d]] + adj[route[b]][route[c]]):
            # 順番を変えた方が改善すると分かった場合、その変更を反映する
            x, y = d, b
            if y - x > a + N - c:
                x, y = c, a + N
            while x < y:
                xx = x if x < N else x - N
                yy = y if y < N else y - N
                route[xx], route[yy] = route[yy], route[xx]
                x += 1
                y -= 1
    ans = calc_total_dist(adj, route)
    return ans, route

まず、先程と同じ問題を2-optで解いてみます。

# 先程と同じ問題を2-optで解いてみる
ans_total_dist, ans_route = two_opt(adj, TL = 2.0)
print(ans_total_dist)
data_id = make_vis_data(cities, ans_route)

print("\nデータ内容の確認")
!cat "tsp_vis_data/{data_id}_out.txt"

実行結果

2.53906867403919
作成したデータ: tsp_vis_data/023317_in.txt, tsp_vis_data/023317_out.txt

データ内容の確認
5 3 7 1 2 4 6 0 9 8

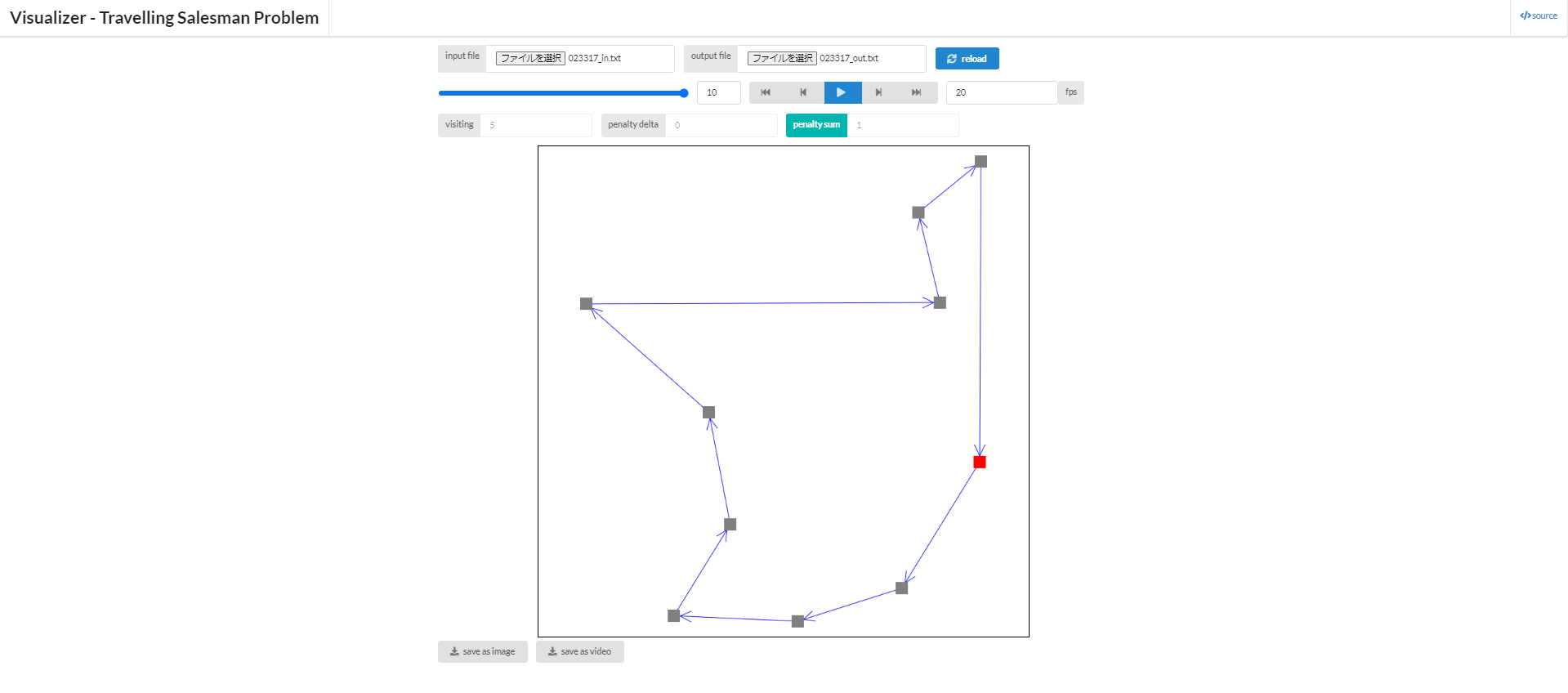
少しだけ経路は異なるものの、確かに殆ど同じ結果が得られていることが分かると思います。 なお、試行によっては、これより少し悪化した解や、先程のbitdpによる解と全く同一の解を得ることもあります。

続いて、先程より規模が大きい問題についても解いてみます。

cities, adj = make_problem(N = 100)
ans, route = two_opt(adj, TL = 2.0)
data_id = make_vis_data(cities, route)

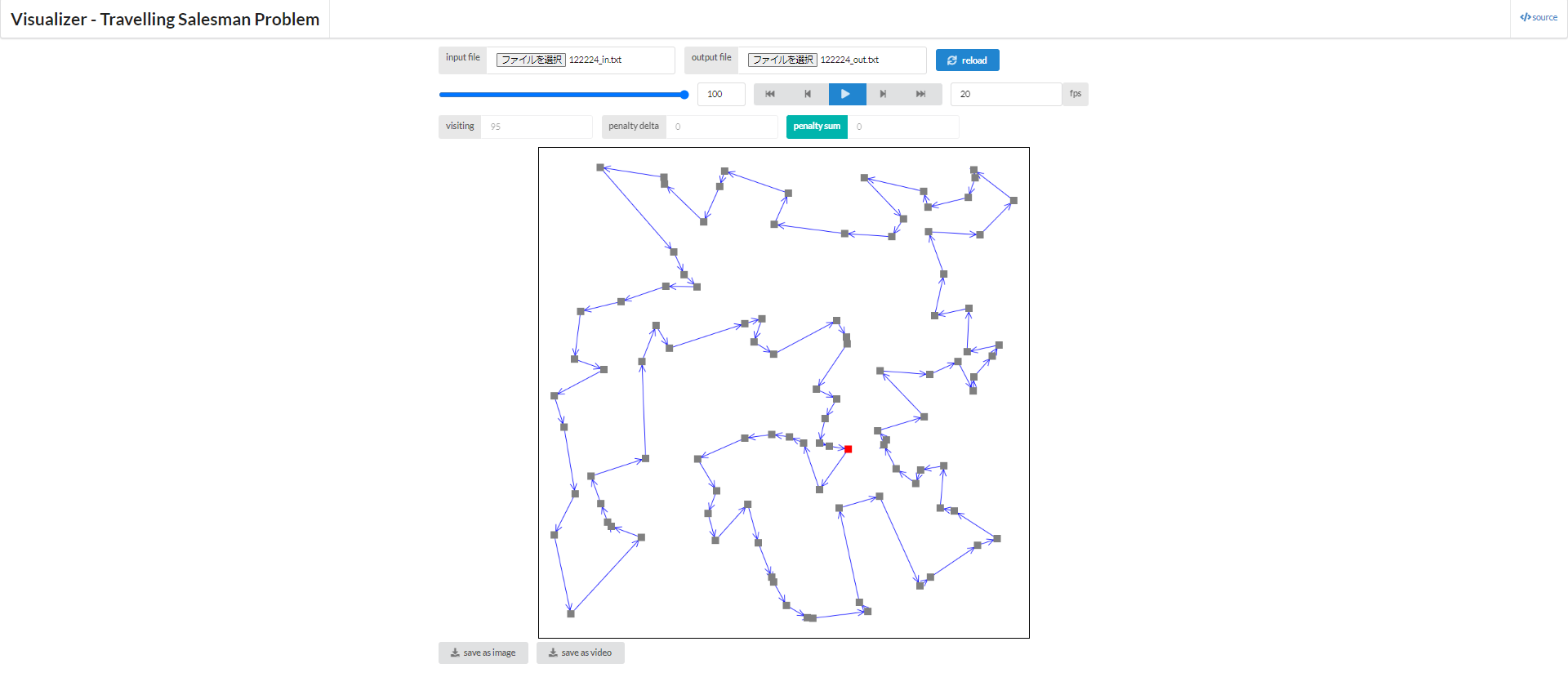
以下に結果を一部掲載しておきます。

[実行制限時間が2秒の場合]

[実行制限時間が10秒の場合]

[実行制限時間が100秒の場合]

どうでしょう、見た感じではかなり妥当そうな解が得られているように思いませんか?

また、なんとなくではありますが、実行制限時間が長くなるにつれて解がよくなっていそう?、ということも同時に掴んでもらえるかも知れません。 当然、実行時間は長ければ長い程より多くの解を探索できるので、解が良くなっているのは事実です。

ただ、2-optで全ての都市の訪問順を得られるわけではないので、どれだけ時間をかけてもこのままだと絶対に最適解が得られない、という事態も発生し得ます。それ故に他の様々な解法も重要になってくるという訳です。

解法3 タブーサーチ

続いて、ここではタブーサーチを用いた解法についてみていきます。
先に断わっておくのですが、タブーサーチについて、私は大して詳しくありません。実際、競プロのコンテストで使用したことはありません。
じゃあやるなよ、という声が聞こえてきそうなものですが、折角教科書等でも紹介されているので、一応色々と調べた上で、絶対的な確信が持てる部分だけをほんの少し書いていきます。

(ちょっとだけ言い訳を書くのですが、Twitter検索で「タブーサーチ」と検索すると、「実装時間が取れる長期コンならタブーサーチとかあってもよさそうだけど全然聞かない。」「メタヒューリスティクスの話にはだいたいタブーサーチが出てくるけど、マラソンマッチでタブーサーチ使って上位に入った人は見たことないのが気になる。」といったような声が散見されます。
ただし、タブーサーチという単語が題名に含まれる論文は大量に存在します。 学術分野よりの手法なのでしょうか。
この辺りの事情に詳しい方がいらっしゃれば、お話を聞きたいものです。)

ここでは、入門タブー探索法というORの記事を主軸にみていくことにします。教科書と大体似たような内容の記事になっています。(なお、タブーサーチとタブー探索法は同一の手法です。)
ここではその一部のみの紹介に留めるので、興味のある方は元記事や教科書の方をご覧下さい。

早速手順の紹介ですが、大まかには以下のようになっています。

タブーサーチ(記事からの引用)

Step1. 初期解$x$を生成する．タブーリスト$T$を初期化する。
Step2. $N(x) \setminus ({x}∪T)$の中で最良の解$x'$を見つけ、$x=x'$とする。
Step3. 終了条件が満たされれば暫定解を出力して探索を終了する。
そうでなければ，タブーリスト$T$を更新した後Step2に戻る。

簡潔にまとめると、悪い解(タブー)には遷移しないことにする局所探索法と言ったイメージです。
ここで注意点ですが、Step2.の$x'$というのは、あくまで$N(x) \setminus ({x}∪T)$の中で最良なだけなので、$x'$が$x$よりも必ず良い解であるという保証はないということに注意してください。そしてそれ故に最良解は必ず保存する必要性があります。

また、タブーサーチを理解するための用語なども整理します。

• 巡回(cycling)
  探索中で移動した解の軌跡が、いくつかの解を経由して元の解に戻ってしまう現象のこと。例えば、局所探索法で「似たような遷移ばかり繰り返していると、同じような解ばかりが得られて」しまうと書きましたが、正にこれが巡回という用語の示す状況です。

• タブーリスト(tabu list)
  移動を禁止する(つまり、タブーにする)解集合のこと。この集合に含まれる解のことを禁止解と言います。タブーリストの作り方としては、直近に訪れた解の集合をそのままタブーリストに据えるものがあったり、後述する属性というものに注目して作成したりする方法があります。
  また、タブーリストは短期メモリ(short term memory)とも言うそうです。(なお、これに関しては教科書の注142に依っていますが、先に示したORの記事では、より狭義に直近の探索履歴のことを短期メモリと表現しており、用語の定義に少し揺れがあるかも知れません。)

• 属性
  タブーリストに記憶する、近傍操作の特徴のこと。この属性集合のことをそのままタブーリストと呼ぶことも。
  現実的な時間内で探索できる解の数は高が知れており、この属性という特徴で、解集合を間接的に表現することによってより効率的にタブーを決定することが出来ます。

以上の用語の説明からも分かる通り、タブーサーチがタブーとするもの、つまり、何を操作として禁止するかは、問題に応じて様々に選択可能であり、それは「解のそのもの」のこともありますし、「解の属性」のこともありますし、「解への遷移」のこともあります、といった感じです。

具体的な実装については省略しますが、
wikiやとある海外のサイトやgithubにあがっている実装例などを見ると良いかと思われます。
(タブーサーチにもう少し自信が持てるような日がくれば追記するかもしれません……。)

なお、一般に多くのアルゴリズムや手法などは、良い結果に注目して計算を進めていくのが普通です。ですが、このタブーサーチは、名前からも明らかな通り、悪い結果に注目して計算を進めていきます。その点はかなり特徴的な手法なのではないでしょうか。
そしてそういった特殊性故に、少しマイナーなのかな、という気がしています。尤も、考え方自体は非常に面白く、ざっくりとした方針に関しては色々応用の仕方があるのかな、とも思いました。
タブーサーチについては、以上です。

解法4 誘導局所探索法

最後にご紹介するのが、局所探索法のところでちらっと紹介させて頂いた誘導局所探索法です。
これについても文言だけではありますが、ほんの少し触れておきます。

ここで紹介する手法は、教科書のp.308の他、この論文の13頁あたりなどでも紹介されている手法でもあります。
(Voudouris, C., & Tsang, E. (1999). Guided local search and its application to the traveling salesman problem. European journal of operational research, 113(2), 469-499.)

具体的に書くと、今までの解法では距離の計算に隣接行列(都市間の距離を表す行列、ここではDとします)を用いてきましたが、それの代わりに、
$$
D'=D+\lambda⋅P=[d_{ij}+ \lambda \cdot p_{ij}]
$$
と表される補助的な隣接行列$D'$を用いる手法になっています。
ここで、$\lambda$は単なるパラメータであり、本質的なのはペナルティに相当する$p_{ij}$です。

このペナルティは誘導局所探索法によって調節される値であって、ざっくりと言えば都市iと都市jの間の距離が長いのにも関わらすペナルティが小さいと、値が増やされていきます。(より詳細には先程の論文や教科書等をご覧ください。)

先程の誘導局所探索法の説明で、この手法は「局所最適解という窪みを埋めてくれるペナルティ関数を持ってきて、その局所最適解から脱出し、真の大域最適解を目指す」ような手法だと述べました。

つまり、ここでは$p_{ij}$がそのペナルティ関数に相当しています。この値が増えていくことによって、現在定めている都市の訪問順序が最適でなくなり、より大域最適解へと近づくことが出来ると言ったイメージです。
確かに何となくだけれども、それでうまく行きそうだ、ということが伝わるでしょうか。この手法に関する説明は、以上になります。

TSPのまとめ

以上、TSPに関する手法をざっくりと4つ紹介させて頂きました。
これはリンクの再掲になりますが、梅谷先生のスライドやHPでは、他にもNearest Neighbor法(最も近い都市に貪欲法的に移動していく手法)や、最近追加法、最近挿入法が扱われています。
他にも、3-opt(辺を3本付け替えるという操作)やor-opt(ある部分路を別の場所に挿入するという操作)、最小全域木を用いた近似解法などが話題としてあります。

(最小全域木に関する近似解法については、高校数学の美しい物語さんでも紹介されています。)

ちなみに、今回は自分でデータを作ってそれをビジュアライズするということに焦点を当てていたので本ビジュアライザを利用させて頂きましたが、先述の通りTSPは有名問題なので、他にも山ほど解説記事やビジュアライザは存在します。

解説記事の一例としては、EEICの方がかなり詳しい記事をQiitaに書いていらっしゃいました。リンク先

また、ビジュアライザに関しては、以下の動画が再生回数的にもそこそこ有名な動画だと思います。
特に、1分33秒から始まるSimulated Annealingという技法を見て頂けると、次に扱う焼き鈍し法のイメージがより掴みやすくなるかと思います。

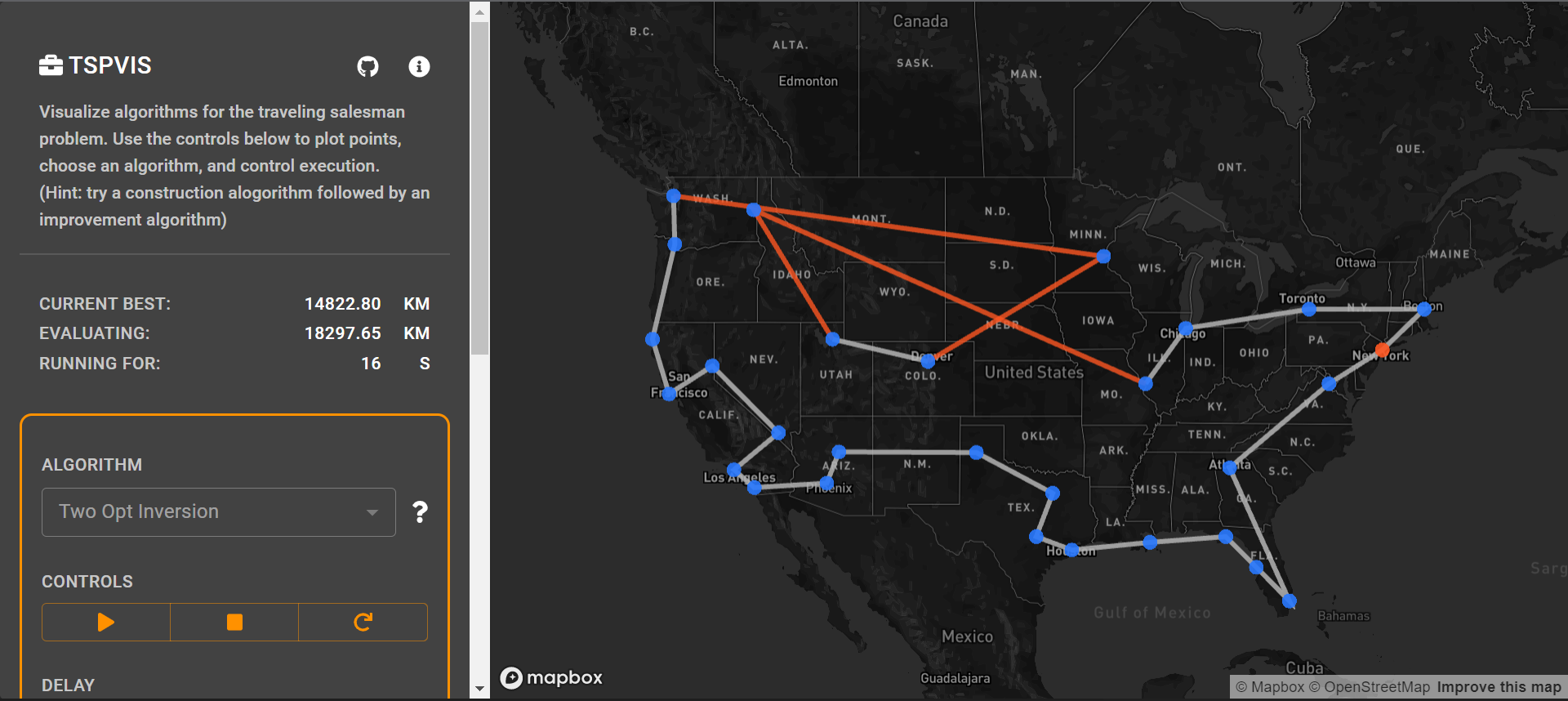
また、自分で色々試して遊べるという点では、TSPVISというサイトが一番凄そうでした。
興味がある方は、是非遊んでみて下さい。

円詰め込み問題

続いて、この項では焼き鈍し法について扱います。

説明

円詰め込み問題とは?

まず、最初に詰め込み問題というジャンルの問題について紹介します。
詰め込み問題という言葉の意味は、ほぼそのままの意味で捉えられますが、基本的に何かしらの図形を互いに重ならないようにするという条件の下で、それらを詰め込んでいくというものです。

この問題の応用例は多岐に渡るそうで、例えば、京都大学 永持研究室のサイトによると、

• 鉄板の切りだし (長方形の容器に長方形を入れる)
• VLSIの設計 (長方形の容器に長方形を入れる. さらに配線の最小化)
• 服の型紙の配置 (長方形の容器に多角形を入れる)
• シュレッダーにかけられた文書の復元 (長方形の容器に多角形を入れる)
• 宝石の原石の削り方 (多面体に多面体を入れる)
• タンパク質のドッキング (球の集合同士を配置)

などなど、色々あるそうです。
梅谷先生のスライドでも、ラスタ図形詰込み問題に対する局所探索法の特徴点抽出を用いた効率化という題名のものがあります。

このことは、競プロの文脈においても同様で、

• CADDi 2019 球の詰め込み
• AHC001 Atcoder Ad

などが該当します。(宣伝: CADDi2019のビジュアライザを作りました。 ←私の過去記事)
場合によっては、

• AHC004 Alien's Genome Assembly

も、近いと言えるかも知れません。
(cf. AtCoder Heuristic Contest 004 (AHC004) 参加記)

さて、本題に戻りますが、ここで扱う問題は、円詰め込み問題です。
以下の画像を見るのが一番分かりやすいかと思います。

つまり、ある枠に対して、出来る限り少ないスペースだけで与えられた円を全て詰め込もう、というのが大雑把な題意になります。

なお、この問題自体は教科書のヒューリスティックの項では扱われてはおらず、
p.77の「非線形計画問題の定式化」という項で扱われています。
実際、この問題は二次計画問題の形式をしており、以下のように定式化可能です。

\begin{aligned}
\textrm{minimize} \quad &L \\
\textrm{subject to} \quad &(x_i-x_j)^2+(y_i-y_j)^2\geq(r_i+r_j)^2 \: (1\leq i<j\leq n)\\
                          &r_i \leq x_i \leq L-r_i \: (∀i\in{1,\dots,n})\\
                          &r_i \leq y_i \leq W-r_i \: (∀i\in{1,\dots,n})\\
\end{aligned}

ここで、円が詰め込まれる枠のことをコンテナと呼ぶことにすると、Lはコンテナの長さ(これを最小化したい)、Wはコンテナの幅(これは固定値)にそれぞれ相当しています。

つまり、上の式は、カジュアルには、

\begin{aligned}
\textrm{minimize} \quad &コンテナの長さ \\
\textrm{subject to} \quad &どの二つの円も互いに交わらない\\
                          &全ての円がコンテナの長さに収まっている\\
                          &全ての円がコンテナの幅に収まっている\\
\end{aligned}

と解釈することもできます。

焼き鈍し法とは?

続いて、焼き鈍し法について説明していきます。
まず、この手法の名前に関する注意ですが、焼き鈍し法とアニーリング法は同じです。 アニーリングという単語は、焼き鈍しの英語になっています。

この焼き鈍しは金属工学における焼き鈍しという現象を模している最適化手法とされていて、その金属工学における焼き鈍しとは、コトバンクによると、

「金属やガラスなどを適当な温度に熱してから、ゆっくりと冷却する操作。内部ひずみの除去、金属の軟化などのために行う。」

というものになっています。

また、simulated annealing (SA)という単語も多スタート局所探索法のところで示しましたが、これも同じ手法のことを指しています。文字通り、コンピューター上でannealingをsimulateするという意味かと思われます。

さらに、メトロポリス法という単語が焼き鈍し法とほぼ同義の意味で使われることもあります。こちらはより熱力学観点から見た手法のようで、焼き鈍し法はメトロポリス法を利用した最適化手法だと言われることもあります。

また、量子コンピューターの分野において量子アニーリングという手法があるそうですが、これの基になったのが、この焼き鈍し法だそうです。(参照元: https://japan.zdnet.com/article/35084549/)

名前に関するあれこれだけでも、色々話題がありますね。

さて、焼き鈍し法の具体的な手順に関してですが、実は山登り法を理解できていれば非常に単純な拡張をするだけで焼き鈍し法のコードは書けてしまいます。
私が初めて焼き鈍し法を学んだ時は、金属工学を先に理解しなければいけないのかと絶望した記憶がありますが、(少なくとも形式をなぞる上では)それらの知識は一切不要です。
焼き鈍しは山登りと本質的に同じであり、山登り法が(ある程度綺麗に)書けているならば機械的に移行可能です。

まず、局所探索法の時と同様に、目的関数$f(x)$を最小化することを目指すという状況を考えます。
山登り法が示していた操作は、今持っている解$x$に対し、近傍$N(x)$を考え、その中から取ってきた一点$x'$に対し、それが改善解ならば必ず採用する、という操作であったことを思い出して下さい。

ここで、

$$
\Delta=f(x')-f(x)
$$

と定めます。つまり、この$\Delta$は新しい解に移ることによって、どのくらい目的関数の値が改善するか、ということを示す値です。小さければ小さいほど、より改善していることを示しています。

そして、遷移確率関数$p(Δ)$ という関数を導入します。
この関数は、「解の改善量$\Delta$に応じて、どのくらいの確率で、実際にその新しい解を採用するか」を表す関数です。
山登り法では、「改善解ならば必ず採用」と定めていたので、遷移確率関数は以下のようになります。

  p(\Delta)=
  \begin{cases}
    1 & \text{if $∆ ≤ 0$} \\
    0 & \text{if $∆>0$}
  \end{cases}

$∆ ≤ 0$ということは、$f(x') \leq f(x)$、つまり、新しい解が元の解よりも良い解であるということです。この時は必ず遷移するのでしたから、遷移確率は100%を意味する1になります。逆に悪くなるのなら、遷移確率は0%を意味する0です。

さて、ここまでくれば、焼き鈍し法の理解まではあと一歩だけです。
焼き鈍し法は、この遷移確率関数を、改悪解となる場合もある程度の確率で採用するよう、次のように書き換えるだけでokです。

  p(\Delta)=
  \begin{cases}
    1 & \text{if $∆ ≤ 0$} \\
    e^{-\Delta/T} & \text{if $∆>0$}
  \end{cases}

どうでしょう、言葉の意味等が少し難しいですが、本質的には相当単純だと思います。ただ、同時に非常に奥が深いのも、これまた事実です。
なお、ここでTは温度関数と呼ばれる関数の値で、詳しくはコード中にて触れています。

ここで、$e^{-\Delta/T}$という数式が謎めいていますが、(T=1の条件のもとで)この関数をグラフにしてみたものが、以下になります。

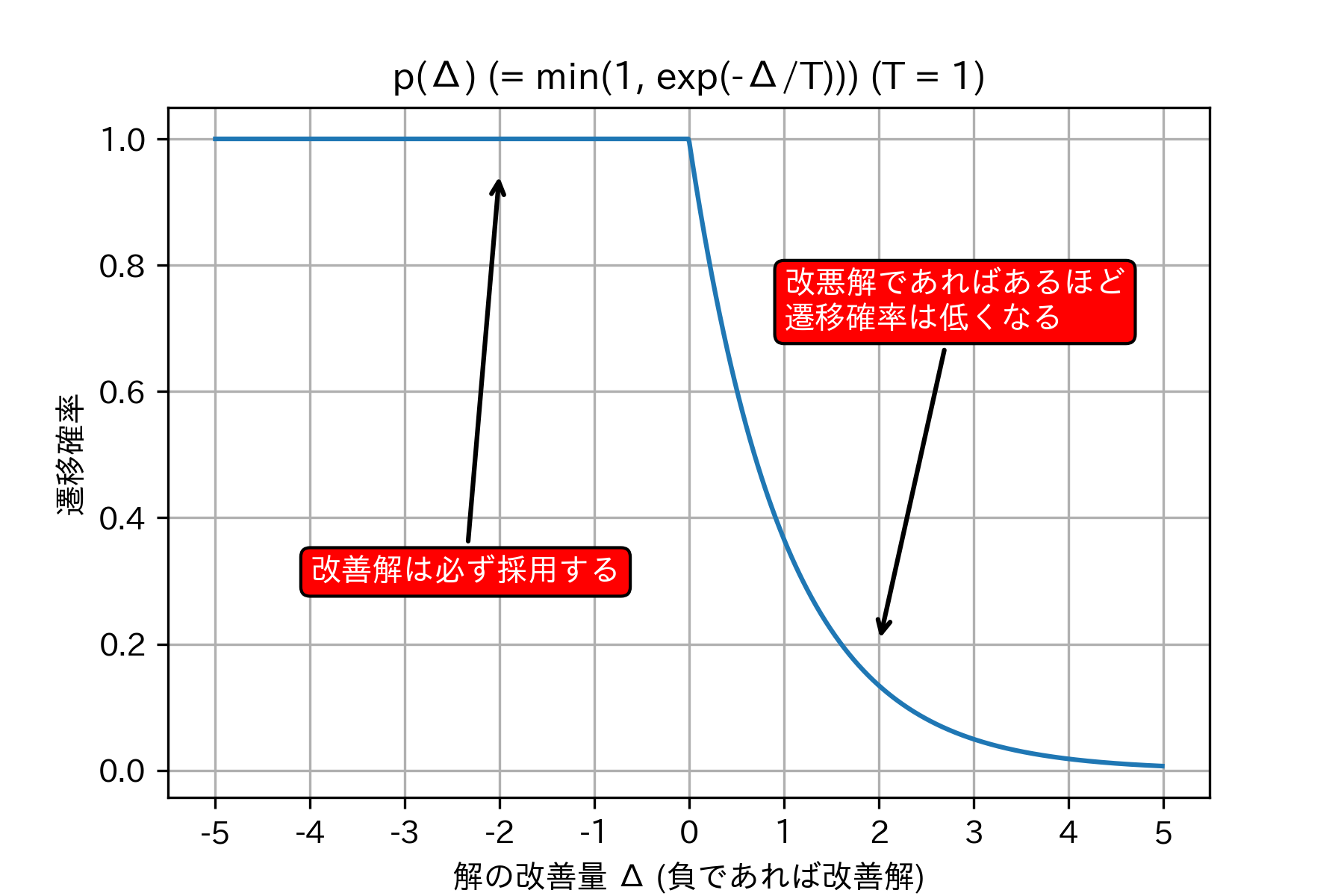
グラフの説明にも書きましたが、$e^{-\Delta/T}$という一見謎な関数は、「改悪解であればあるほど採用する確率を小さくした方が良い」と言う、直感的な事実を数式に書き起こしたものとも捉えられます。もう少し詳しい説明も後程紹介します。

なお、この説明では分かりにくいと思う方もいらっしゃるかと思われますが、この説明以外にも、教科書の説明や、ネット上に落ちている素晴らしい説明などが沢山あります。これらも合わせてご覧下さい。

[資料]

• 診断人さんによるめちゃくちゃ詳しい資料 焼きなまし法のコツ Ver. 1.3 (https://shindannin.hatenadiary.com/entry/2021/03/06/115415)
• gasinさんによるc++のコード付きの資料 誰でもできる焼きなまし法 (https://gasin.hatenadiary.jp/entry/2019/09/03/162613)
• hakomoさんによるgithubの資料 (https://github.com/hakomo/Simulated-Annealing-Techniques)

実践

では、以下実際に円詰め込み問題を焼き鈍し法で解いていきます。
まず、問題生成用の関数とビジュアライズ用関数をそれぞれ定めます。非本質部分なので、読む必要はありません。

# 見る必要なし
def make_circle_packing_problem(N: int = 20) -> Tuple[List[float], float]:
    """円詰め込み問題をランダムに作成

    Args:
        N (int, optional): 円の数 デフォルト値は20

    Returns:
        以下の二つのTuple
        prob (List[float]): 問題(円の半径)
        W (float): コンテナの幅
    """
    prob = [0.5 + random.random() / 2 for _ in range(N)]
    W = 5.0 + random.random() * 1.0
    return prob, W


# 見る必要なし
def vis_circle_packing_problem(prob: List[float], W: float,
                               ans: List[Tuple[float, float]],
                               ans_L: float) -> None:
    """ビジュアライズ用関数

    Args:
        prob (List[float]): 問題(円の半径)
        W (float): コンテナの幅
        ans (List[Tuple[float, float]]): 答え(x座標とy座標のTuple)
        ans_L (float): コンテナの長さ
    """
    N = len(prob)
    maxL = 0
    for i in range(N):
        maxL = max(maxL, ans[i] + prob[i])
    if maxL == 0:
        assert False
    fig, ax = plt.subplots()
    fig.set_figheight(W)
    fig.set_figwidth(maxL)
    ax.set_xlim(0, maxL)
    ax.set_ylim(0, W)
    ax.set_aspect('equal')
    ax.grid()
    for i in range(N):
        ax.add_patch(patches.Circle(xy=(ans[i], ans[N+i]),
                                    radius=prob[i],
                                    facecolor=plt.cm.jet(int(i/N*255))))
    ax.set_title(f"N: {N} L:{ans_L}")
    fig.suptitle("circle packing problem")
    plt.show()

以下からが重要な部分です。特に焼き鈍し法に関する部分を見て頂ければと思います。

# パラメータ等

# TIME_LIMIT (TL) 焼き鈍し法を何秒間行うかを示します
# 今回は分かりやすさの為、高速化を一切していません
# そのため、TLは長めにとってあります
TIME_LIMIT = 10.0
# start_temp, end_temp 温度関数の為のパラメータ ここの調節はかなり重要です
# 場合によってはOptunaなどを用いて調節することもあります
start_temp, end_temp = 100.0, 0.01
# ビジュアライザ用のパラメータ 重要ではありません
ANIMATION_INTERVAL = 100


# 以下、関数  特にsolve関数が重要になっており、他は流し見て頂ければ大丈夫です

def is_valid(prob: List[float], ans: List[float], W: float) -> bool:
    """答えが問題の制約を満たすか確かめる

    Args:
        prob (List[float]): 問題(円の半径)
        ans (List[float]): 答え(x座標をN個、y座標をN個を順に並べたもの)
        W (float): コンテナの幅

    Returns:
        bool: 制約を見てしているかどうか
    """
    N = len(prob)
    for i in range(N):
        for j in range(i+1, N):
            if (ans[i]-ans[j])**2+(ans[N+i]-ans[N+j])**2 < (prob[i]+prob[j])**2:
                return False
    for i in range(N):
        if not prob[i] <= ans[i]:
            return False
        if not (prob[i] <= ans[N+i] <= W-prob[i]):
            return False
    return True


def get_maxL(prob: List[float], ans: List[float]) -> float:
    """コンテナの長さを取得する

    Args:
        prob (List[float]): 問題(円の半径)
        ans (List[float]): 答え(x座標をN個、y座標をN個を順に並べたもの)

    Returns:
        float: コンテナの長さ
    """
    N = len(prob)
    maxL = 0
    for i in range(N):
        maxL = max(maxL, ans[i]+prob[i])
    return maxL


def calc_score(prob: List[float], ans: List[float]) -> float:
    """目的関数の値を計算する

    Args:
        prob (List[float]): 問題(円の半径)
        ans (List[float]): 答え(x座標をN個、y座標をN個を順に並べたもの)

    Returns:
        float: 目的関数の値 本来はmaxL(つまり、コンテナの長さ)だけが目的関数であるが、
               最適化の方向性を分かりやすくするため、円のx座標の総和の合計も足してある
    """
    return 100.0*(10.0*get_maxL(prob, ans)+sum(ans[0:len(ans)//2]))


def modify(ans: List[float]) -> List[float]:
    """今持っている解の近傍にある解を一つ生成する

    Args:
        ans (List[float]): 答え(x座標をN個、y座標をN個を順に並べたもの)

    Returns:
        List[float]: 新しい解
    """
    new_ans = ans[:]
    idx=random.randrange(len(new_ans)//2)
    new_ans[idx] += 0.5-random.random()
    new_ans[idx+len(ans)//2] += 0.5-random.random()
    return new_ans


def make_first_solution(prob: List[float], W: float) -> List[float]:
    """初期解をランダムに一つ生成する
    ただし、制約を満たす範囲内で、ある程度詰めた状態の解を生成する

    Args:
        prob (List[float]): 問題(円の半径)
        W (float): コンテナの幅

    Returns:
        List[float]: 初期解
    """
    N = len(prob)
    ans0 = [prob[0] + 0.01]
    for i in range(1, N):
        ans0.append(ans0[-1]+prob[i-1]+prob[i]+0.01)
    ans0 += [random.uniform(prob[i], W-prob[i]) for i in range(N)]
    assert is_valid(prob, ans0, W)
    for i in range(1, N):
        while is_valid(prob, ans0, W):
            ans0[i] -= 0.1
        ans0[i] += 0.1
    return ans0


def solve(prob: List[float], W: float):
    """円詰め込み問題を解く

    Args:
        prob (List[float]): 問題(円の半径)
        W (float): コンテナの幅

    Returns:
        以下の二つのTuple
        hist (List[List[float]]): 探索履歴
        best_ans (List[float]): 答え
    """
    ans0 = make_first_solution(prob, W)

    best_score = calc_score(prob, ans0)
    best_ans = ans0
    hist = []
    loop_cnt = 0

    # ここが重要! 焼き鈍し法
    start_time = time.perf_counter()
    while time.perf_counter()-start_time < TIME_LIMIT and len(hist) < 10000:
        loop_cnt += 1

        # 解に変形を加えて、その新しい解のスコアを求めます
        new_ans = modify(best_ans)
        if not is_valid(prob, new_ans, W):
            continue
        new_score = calc_score(prob, new_ans)

        # 温度関数
        # start_tempとend_tempはそれぞれパラメータで、時間に応じて線形に移行していきます
        # この部分にはいくつかバリエーションが存在します
        temp = start_temp + (end_temp - start_temp) * (time.perf_counter()-start_time) / TIME_LIMIT
        
        # 遷移確率関数 np.clipとしているのは、単に計算上の都合であって非本質的です
        probability = math.exp(np.clip((best_score - new_score)/temp,-10.0,0.0))

        # 山登り法の場合の遷移確率関数は、以下のようになります
        # probability=(1 if best_score>=new_score else 0)

        # 遷移確率に従って実際に遷移するかを決めます
        if probability >= random.random():  # 遷移をする場合、
            best_score = new_score  # スコアと解を更新します
            best_ans = new_ans

        # これはビジュアライザ用に答えを保存しているだけで、非本質的部分です
        if loop_cnt % 50 == 0:
            hist.append(best_ans[:])

    assert is_valid(prob, best_ans, W)
    print("ループ回数: ", loop_cnt)
    print("最終的なスコア: ", best_score)
    return hist, best_ans

prob, W = make_circle_packing_problem(N=20) # 問題を一つ作成します

hist, ans = solve(prob, W) # 問題を解いて、
vis_circle_packing_problem(prob, W, ans, get_maxL(prob, ans)) # それをビジュアライズします

実行結果

ループ回数:  137606
最終的なスコア:  17086.518188430007

また、焼き鈍しの過程を動画形式で表示するためのコードも書きました。
これを実行して、その過程を見てみます。

動画生成用コード

# 見る必要なし

ANIMATION_INTERVAL = 100

list_of_ans=hist

N = len(prob)
maxL = 0
for i in range(N):
    maxL = max(maxL, list_of_ans[0][i] + prob[i])
if maxL==0:
    assert False
maxL *= 1.2

fig = plt.figure()
ax = fig.add_subplot(111)
fig.set_figheight(W/1.5)
fig.set_figwidth(maxL/3.0)
fig.suptitle("Circle Packing Problem", fontsize=20)
ax.set_xlim(0, maxL*2.0/3.0)
ax.set_xlabel("L")
ax.set_ylim(0, W)
ax.set_ylabel("W")
ax.set_aspect('equal')
ax.set_title(f"N={N}, W={W}")
ax.grid()

text_var = None

def _update(frame: int) -> None:
    # 描画
    ax.patches.clear();
    for i in range(N):
        ax.add_patch(patches.Circle(xy=(list_of_ans[frame][i],
                                        list_of_ans[frame][N+i]),
                                    radius=prob[i],
                                    facecolor=plt.cm.jet(int(i/N*255))))
    return (ax,)

anim = animation.FuncAnimation(fig, _update,
                               interval=ANIMATION_INTERVAL,
                               frames=len(list_of_ans))

以下がその動画です。

HTML(anim.to_html5_video())

状況を改めて整理すると、今考えている問題は、$L$、つまり、コンテナの長さを最小化するということでした。円が左に移動してくれれば改善解、円が右に移動してしまうと改悪解です。
なお、ここでは遷移、つまり、解にどのような変形を加えるかというのは、ある一つの円をランダムな方向に少しずらすという操作で定めてあります。

この動画から、

• 初期の段階、つまり高温の時ほど激しく(改悪解への)遷移が起きる点
• 段々と低温になるに従って遷移が少なくなっていく点
• そしてこのように改悪解への遷移を許容しているが故に、よりより局所最適解へと移行できる点

などが見て取れるかな、と思っています。
これらの特徴は焼き鈍し法を使用した場合のビジュアライズ結果として典型的な特徴です。
ただし、逆にこれらの特性が場合によっては仇となり得るので、その点には十分な注意が必要です。

焼き鈍し法に関する他のビジュアライズ結果としては、多点スタートのところでお見せしたtouristのAHC002の解の最後や、tspのところでお見せした動画のSimulated Annealingの部分などが挙げられます。これらでも、似たようなことが確認できるかと思います。
他にもAHC009やAHC001というコンテストでも焼き鈍しをしている方が多かったです。

#AHC001 お疲れ様でした．
暫定スコア 486.9 億点，148位でした．

焼き鈍しです．ときどき形を矯正したり破壊したりして，いいスコアになる state を探しました．
typescript でビジュアライザを作って，スコアが悪い問題を観察しながら進めていました．せっかくなので動画を貼ってみます． pic.twitter.com/BxxjMkuJb6

— si (@iiljj) March 14, 2021

焼き鈍し法の、ビジュアライズ結果としてのイメージも、掴んで頂けたら幸いです。

最後に、expについて少しだけ説明します。
以下は、Introduction to Heuristics Contest 解説というpdfからの引用です。
同じ様な内容、および、より発展的内容が、焼きなまし法の真実というサイトにも掲載されています。

p(∆, T) の設計思想

$e^{∆/T}$という採用確率には以下のような意図があります。
今、解 A から解 B に至る変形と、解 B から解
C に至る変形、解 A から解 C に直接至る変形の 3 つがあったとしましょう。
各変形におけるスコアの増加量は全て負で、それぞれ $∆_{AB}、∆_{BC}、∆_{AC}$ であったとします。
スコアの変化量の合計は途中に経由する解によらないため、
$$
∆_{AC} = ∆_{AB} + ∆_{BC}
$$
が成り立ちます。
この時、A → B と B → C の変形がともに採用される確率は

\begin {align}
    &p(∆_{AB}, T)p(∆_{BC} , T)  \\ 
    &= e^{∆_{AB}/T}e^{∆_{BC} /T} \\  
    &= e^{(∆_{AB}+∆_{BC} )/T}   \\
    &= e^{∆_{AC} /T}  \\
\end {align}

となり、A から C への直接の変形の採用確率と等しくなります。
つまり、変形列の長さによらず、始地点と終地点のスコアの差に応じて採用確率が決まります。
このため、広いが低い小高い丘のような局所解から抜け出し長くゆるやかな坂を下った先にある高い山へ到達することが容易となります。
一方で、尖っている針のような局所解から数歩先にあるより高い針の先へ到達することは困難です。局所解から抜け出すための他の方針としては変形操作を大きくする (例えば 2 点スワップでなく 3 点スワップにするな
ど) 方針があります。
この方向性の場合は逆に、広いが低い小高い丘のような局所解から抜け出すことが困難になる代わりに、尖った針のような局所解から近くのより高い針の先へと直接移動することが出来るようになります。

極めて簡潔にまとめるならば、指数法則の公式が成立するが故に、都合が良いと言ったところでしょうか。

類似した他の手法

以上で焼き鈍し法自体に関する説明は終わりですが、
これに類似した手法を簡潔に二つほど紹介します。なお、どちらも知名度としては焼き鈍し法よりも低いと思われます。

• 大洪水法(great delude method, GD)
  wikiの他にも、この論文などでも詳しく書かれています。
  (Turabieh, H., & Abdullah, S. (2011). An integrated hybrid approach to the examination timetabling problem. Omega, 39(6), 598-607.)

詳細は以下にあげた論文内の画像を見て頂きたいですが、「どの程度の改悪解まで遷移を許容するのか」というのを段階的に厳しくしていく、という点で、焼き鈍し法の温度関数に似た雰囲気を感じる手法になっています。

• 閾値受理法(threshold accepting method, TA)
  wikiには恐らく記事がありませんが、COMISEFというサイトには説明がありました。
  ほぼ名前から推察される通りといった感じですが、どの程度の改悪を許容するかというのを固定値にしている手法で、焼き鈍し法や大洪水法よりもさらに簡略な手法になっています。

まとめ

• 焼き鈍し法は山登り法の拡張
• 極めて応用が広い
• いい資料が本当に豊富 これらを見ないのはもったいない! 是非それらもご覧下さい!

長方形詰め込み問題

続いて、BLF法について扱います。

説明

長方形詰め込み問題とは?

長方形詰め込み問題については、この梅谷先生によるORの記事や、同じく梅谷先生によるスライドに関連した話になっています。

長方形詰め込み問題の設定としては、様々な大きさの長方形(製品)を、二次元平面(母材、つまり、長方形を詰め込む枠のこと)上に重なりなく配置する、というものになっています。

数式で状況を定義すると、以下の通りです。

• 条件1
  長方形$i$は母材上に配置される。

    0 \leq x_i \leq W-w_i \\  
    0 \leq y_i \leq H-h_i \\

• 条件2
  長方形対$i,j$は互いに重ならない。
  則ち、以下の四つの不等式の内、一つ以上が成立する。

    x_i+w_i \leq x_j  (iがjの右側) \\
    x_j+w_j \leq x_i  (iがjの左側) \\
    y_i+h_i \leq y_j  (iがjの下側) \\
    y_j+h_j \leq y_i  (iがjの上側) \\

なお、この「一つ以上」という制約がこの問題において本質的であり、これ故に線形計画問題よりも解くことが困難な問題になっています。

長方形詰め込み問題は、より個別的には、2次元ナップサック問題(いくつかの製品を選んで価値を最大化)や、2次元ビンパッキング問題(母材が複数与えられるので、その使用数を最小化)などがあります。
そしてここで扱う問題はストリップパッキング問題と呼ばれる問題で、
高さ可変の母材に対して製品を上手く詰めていき、その高さを最小化することを目指していきます。(なお、以下ではストリップパッキング問題のことを指して、長方形詰め込み問題と呼ぶことにします)

BLF法とは?

さて、先の項で長方形詰め込み問題、特に、ストリップパッキング問題という問題について説明しましたが、この問題に対して有効に働くとされる手法の一つがBLF(Bottom Left Fill)法です。

今回は先にビジュアライザ結果を見た方が分かりやすいと思うので、まず、以下の図を見て下さい。

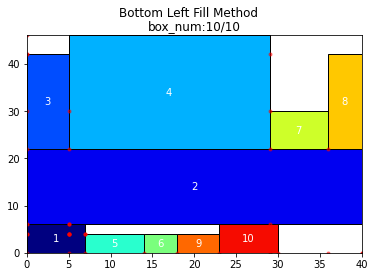
この図が長方形詰め込み問題に対してBLF法を適用した結果になっています。

また、BL安定点という用語も重要です。
数理計画用語集の定義では、

アイテムを重なりなく置ける位置の中で，左方向にも下方向にも並進させることができない位置を BL安定点 という．

という風になっています。図では、これが赤色の点で示されています。
そして、そのBL安定点の内、y座標が最も小さい点(y座標が同じ点が複数存在する時は、x座標が最も小さい点)をBL点と言います。

BLF法はこのBL点に長方形を順次置いていくだけという、かなりシンプルな手法です。しかし、これでかなりうまく行くというのが面白い点です。以下では具体的にそのことを確かめていきます。

実践

以下のプログラムは、梅谷先生のHPにある、
「2005〜2007年度に電気通信大学で実施したシステム工学実験のサンプルプログラム」 (c言語)を、私がPythonに翻訳し、かつpltによる可視化のコードを付け足したものになっています。

データ
解くべき問題となるデータも包含されていたので、それを利用させて頂いています。

データ定義用コード

N1 = "w= 40\nn= 10\n7 6\n40 16\n5 20\n24 24\n7 4\n4 4\n7 8\n4 20\n5 4\n7 6"
N2 = "w= 30\nn= 20\n23 9\n19 4\n12 21\n6 4\n7 13\n9 4\n4 6\n23 6\n16 6\n4 14\n14 6\n6 6\n5 4\n4 6\n6 4\n7 6\n14 11\n4 7\n8 4\n14 4"
N3 = "w= 30\nn= 30\n10 6\n4 4\n4 5\n3 5\n10 5\n3 5\n7 13\n3 4\n8 32\n3 23\n6 4\n3 15\n9 6\n3 3\n3 4\n6 18\n7 5\n3 4\n5 3\n3 8\n5 4\n3 5\n3 3\n5 8\n5 16\n10 13\n3 3\n10 17\n5 14\n5 3"
N4 = "w= 80\nn= 40\n61 38\n7 4\n9 5\n5 4\n5 7\n7 7\n9 15\n4 4\n4 4\n32 31\n4 4\n5 4\n8 10\n4 4\n5 5\n32 4\n7 7\n5 4\n5 8\n7 24\n5 4\n10 7\n4 7\n20 7\n5 7\n5 12\n5 4\n11 7\n8 21\n9 4\n5 72\n5 52\n5 4\n9 7\n5 12\n9 33\n4 8\n9 34\n4 4\n29 4"
N5 = "w= 100\nn= 50\n25 10\n74 8\n27 19\n64 34\n74 6\n39 6\n48 7\n11 10\n8 10\n14 6\n6 10\n26 6\n27 6\n6 10\n8 10\n31 10\n23 6\n7 10\n6 10\n11 10\n53 7\n20 6\n46 10\n18 6\n10 6\n10 10\n9 6\n7 6\n11 6\n7 6\n6 8\n9 7\n47 7\n10 7\n7 6\n25 10\n26 8\n36 6\n6 6\n6 7\n20 6\n16 22\n20 14\n10 6\n14 8\n8 6\n7 6\n16 6\n8 6\n15 6"

Ns = [N1, N2, N3, N4, N5]

for i in range(5):
    if not os.path.exists("blf_prob_data"):
        os.mkdir("blf_prob_data")
    with open(f"blf_prob_data/N{i + 1}.txt", mode='w') as f:
        f.write(Ns[i])

BLF法

NUM_ERROR = 0.001
n = None  # 長方形の数
MAX_N = 1000  # 長方形の最大数
bl_num = 0  # BL安定点の候補数
strip_width, strip_height = None, None  # 母材(枠)の幅，高さ

# あとで出てくる変数
#  w,h: 長方形iの幅(w)と高さ(h)を格納する配列
#  x,y: 長方形iの座標(x,y)を格納する配列
#  blx,bly: BL安定点の候補を格納する配列
#  blw,blh: BL安定点の上，右方向の隙間の幅を格納する配列

ビジュアライズ用コード

def vis(box_num: int, show_bl_stable_points:bool,w,h,x,y,blx,bly):
    # (BLF法理解のためには)重要でない
    global strip_height

    # 母材の高さを計算
    strip_height = 0.0
    for i in range(box_num):
        if(y[i]+h[i] > strip_height):
            strip_height = y[i]+h[i]

    # 画像を生成・表示
    fig, ax = plt.subplots(figsize=(10,6),facecolor="white")
    ax.set_xlim(0, strip_width)
    ax.set_ylim(0, strip_height)
    ax.set_title(f"box_num:{box_num}/{n}")
    
    # 長方形の表示
    for i in range(box_num):
        ax.add_patch(
            patches.Rectangle(
                (x[i], y[i]),
                w[i],
                h[i],
                edgecolor='black',
                facecolor=plt.cm.jet(int(i/n*255)),
                fill=True
            ))
        ax.text(x[i]+w[i]/2, y[i]+h[i]/2, str(i+1),
                color='white', ha='center', va='center')
    
    # BL安定点の表示
    if show_bl_stable_points:
        cnt=0
        for bl_x, bl_y in zip(blx, bly):
            if bl_x is None or bl_y is None:
                break
            ax.plot(bl_x, bl_y, marker='.', color='red', alpha=0.5)
            cnt+=1
        assert cnt==bl_num,f"cnt:{cnt},bl_num:{bl_num}"
    
    fig.suptitle("Bottom Left Fill Method")
    plt.savefig(f"res_{box_num}")

そして、以下の関数がBLF法において最も重要な関数になっています。

def bottom_left_fill(c: int,w,h,x,y,blx,bly,blw,blh):
    # 重要!!!
    # BLF法 (1ステップ分、つまり、長方形を1つだけ設置する)
    
    # 長くて少し難しいように感じるかも知れませんが、
    # 本質的には以下の二つのことをしているだけです
    #  - Step1. BL安定点の内、最良のものを選択し、長方形を設置する
    #  - Step2. この長方形によって生じる新たなBL安定点を追加する
    # 以上のことを踏まえて読んでください
    
    global bl_num
    min_x, min_y = 0.0, 0.0  # 長方形cの配置可能な座標
    collision_flag = False  # 長方形cの重なり判定に用いるフラグ
    i, j = 0, 0

    # 長方形cを配置するBL安定点の候補を選ぶ
    min_x = min_y = 1e9
    for i in range(bl_num):
        # BL安定条件のチェック
        if(w[c] > blw[i]+NUM_ERROR and h[c] > blh[i]+NUM_ERROR):
            # 制約条件のチェック
            if(blx[i] >= 0.0 and blx[i]+w[c] <= strip_width and bly[i] >= 0.0):
                collision_flag = False
                for j in range(c):  # 既に設置した長方形との衝突を見る
                    if(blx[i] < x[j]+w[j]-NUM_ERROR
                       and blx[i]+w[c] > x[j]+NUM_ERROR
                       and bly[i]+h[c] > y[j]+NUM_ERROR
                       and bly[i] < y[j]+h[j]-NUM_ERROR):
                        collision_flag = True
                        break
                if(collision_flag is False
                   and (bly[i] < min_y or (bly[i] < min_y + NUM_ERROR and blx[i] < min_x))):
                    min_x = blx[i]
                    min_y = bly[i]

    #   長方形cの配置座標を決定
    if(min_x < 1e9 and min_y < 1e9):
        x[c] = min_x
        y[c] = min_y

    #   長方形cと母材によって新たに生じるBL安定点の候補を追加
    blx[bl_num] = x[c]+w[c]
    bly[bl_num] = 0.0
    blw[bl_num] = 0.0
    blh[bl_num] = y[c]
    bl_num += 1
    blx[bl_num] = 0.0
    bly[bl_num] = y[c]+h[c]
    blw[bl_num] = x[c]
    blh[bl_num] = 0.0
    bl_num += 1

    # 長方形cと他の長方形jによって生じるBL安定点の候補を追加
    for j in range(c):
        # 長方形cが長方形jの左側にある場合
        if(x[c]+w[c] < x[j]+NUM_ERROR and y[c]+h[c] > y[j]+h[j]+NUM_ERROR):
            blx[bl_num] = x[c]+w[c]
            bly[bl_num] = y[j]+h[j]
            blw[bl_num] = x[j] - (x[c]+w[c])
            if(y[c] > y[j]+h[j]):
                blh[bl_num] = y[c] - (y[j]+h[j])
            else:
                blh[bl_num] = 0.0
            bl_num += 1

        # 長方形cが長方形jの右側にある場合
        if(x[j]+w[j] < x[c]+NUM_ERROR and y[j]+h[j] > y[c]+h[c]+NUM_ERROR):
            blx[bl_num] = x[j]+w[j]
            bly[bl_num] = y[c]+h[c]
            blw[bl_num] = x[c] - (x[j]+w[j])
            if(y[j] > y[c]+h[c]):
                blh[bl_num] = y[j] - (y[c]+h[c])
            else:
                blh[bl_num] = 0.0
            bl_num += 1

        # 長方形cが長方形jの下側にある場合
        if(y[c]+h[c] < y[j]+NUM_ERROR and x[c]+w[c] > x[j]+w[j]+NUM_ERROR):
            blx[bl_num] = x[j]+w[j]
            bly[bl_num] = y[c]+h[c]
            if(x[c] > x[j]+w[j]):
                blw[bl_num] = x[c] - (x[j]+w[j])
            else:
                blw[bl_num] = 0.0
            blh[bl_num] = y[j] - (y[c]+h[c])
            bl_num += 1

        # 長方形cが長方形jの上側にある場合
        if(y[j]+h[j] < y[c]+NUM_ERROR and x[j]+w[j] > x[c]+w[c]+NUM_ERROR):
            blx[bl_num] = x[c]+w[c]
            bly[bl_num] = y[j]+h[j]
            if(x[j] > x[c]+w[c]):
                blw[bl_num] = x[j] - (x[c]+w[c])
            else:
                blw[bl_num] = 0.0
            blh[bl_num] = y[c] - (y[j]+h[j])
            bl_num += 1

最後にメイン関数を定義します。

def main(problem_number: int, show_bl_stable_points:bool):
    global strip_width, strip_height, n, bl_num

    # 以下は事前準備 あまり重要でない

    # 長方形iの幅w[i]と高さh[i]を格納する配列
    w = [None for _ in range(MAX_N)]
    h = [None for _ in range(MAX_N)]

    # 長方形iの座標(x[i],y[i])を格納する配列
    x = [None for _ in range(MAX_N)]
    y = [None for _ in range(MAX_N)]

    # BL安定点の候補を格納する配列
    blx = [None for _ in range(MAX_N * MAX_N // 2 + 1)]
    bly = [None for _ in range(MAX_N * MAX_N // 2 + 1)]

    # BL安定点の上，右方向の隙間の幅を格納する配列
    blw = [None for _ in range(MAX_N * MAX_N // 2 + 1)]
    blh = [None for _ in range(MAX_N * MAX_N // 2 + 1)]

    # 入力データの読込み
    with open(f"blf_prob_data//N{problem_number}.txt", mode='r') as f:
        weq, wstr = f.readline().split()
        assert(weq == "w=")
        neq, nstr = f.readline().split()
        assert(neq == "n=")
        strip_width = int(wstr)
        n = int(nstr)
        for i in range(n):
            ww, hh = map(int, f.readline().split())
            w[i] = ww
            h[i] = hh

    print(f"n = {n}")
    vis_interval = n//10

    # 開始時刻の設定
    start_time = time.perf_counter()

    # BL安定点の候補を格納する配列を初期化
    blx[0] = bly[0] = blw[0] = blh[0] = 0.0
    bl_num = 1


    # !!!ここが重要!!! BLF法の実行
    for i in range(n):
        bottom_left_fill(i,w,h,x,y,blx,bly,blw,blh)
        if i % vis_interval == 0 or i == n-1:
            vis(i+1, show_bl_stable_points,w,h,x,y,blx,bly)


    # 以下は事後処理 あまり重要でない
    # 実行時間の測定
    search_time = time.perf_counter()-start_time

    # 母材の高さを計算
    strip_height = 0.0
    for i in range(n):
        if(y[i]+h[i] > strip_height):
            strip_height = y[i]+h[i]

    # 充填率を計算
    area = 0.0
    for i in range(n):
        area += w[i] * h[i]
    efficiency = area / (strip_width * strip_height) * 100.0

    print(f"search_time = {search_time:.05}[s]")
    print(f"efficiency = {efficiency:.05}[%]")

では実際に走らせてみます。
まず、長方形が10個の場合についてやってみます。

main(problem_number=1, show_bl_stable_points=True)

実行結果

n = 10
search_time = 1.6363[s]
efficiency = 86.957[%]

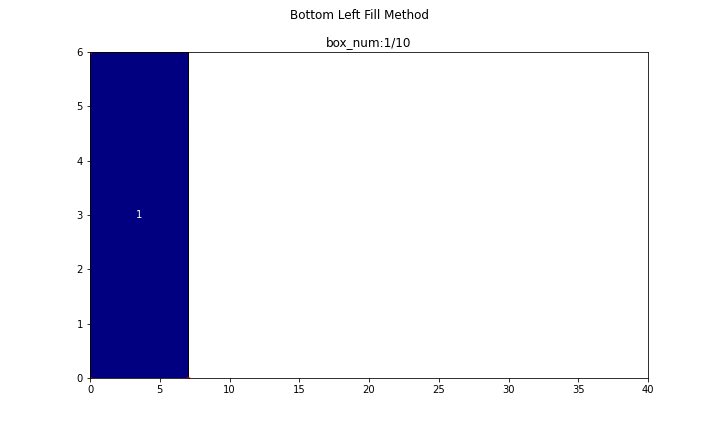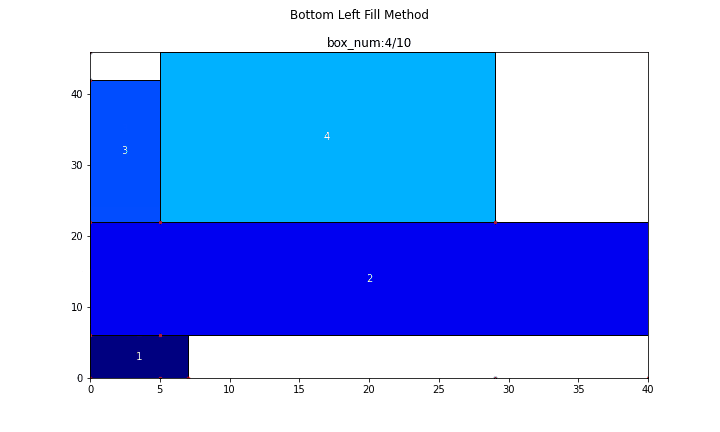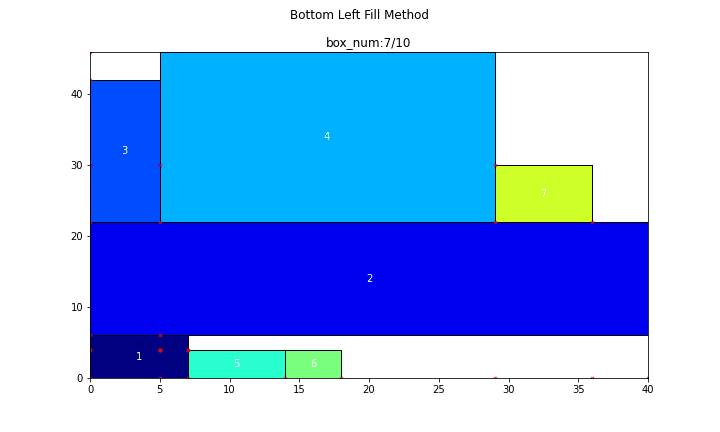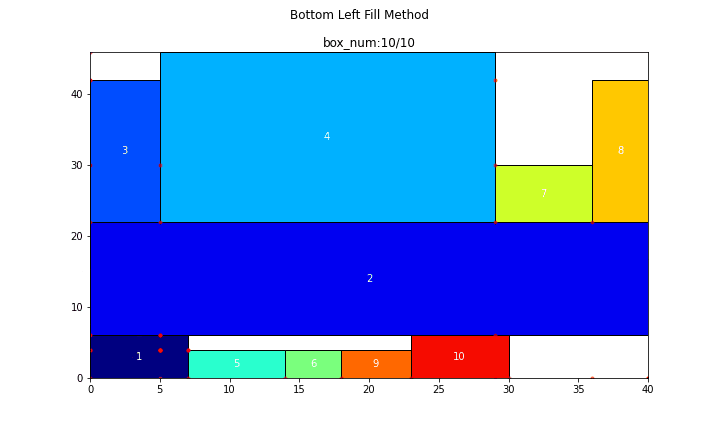
続いて、長方形が50個の場合

main(problem_number=5, show_bl_stable_points=True)

実行結果

n = 50
search_time = 8.7015[s]
efficiency = 89.286[%]

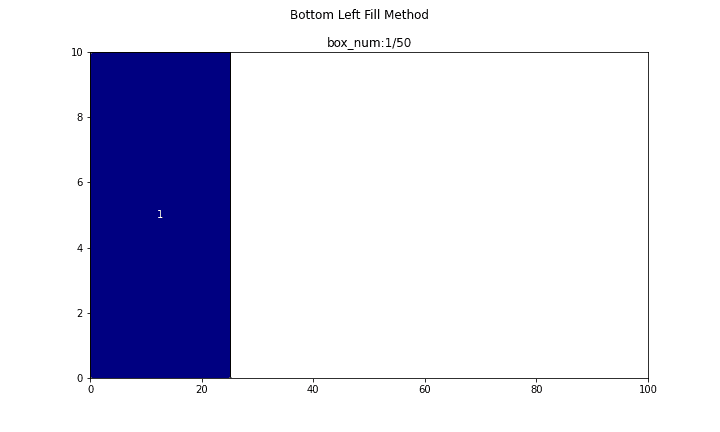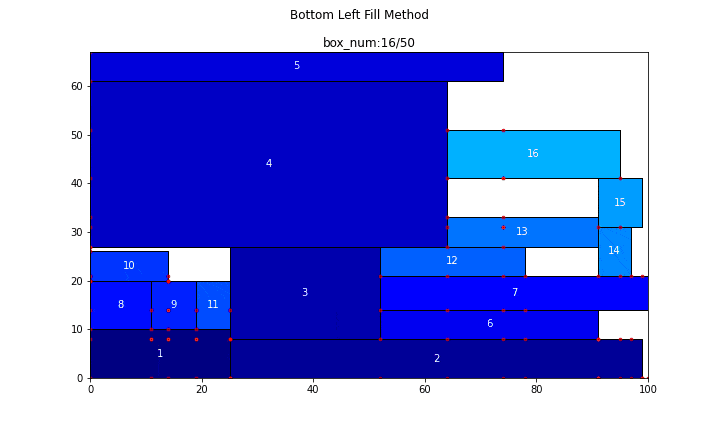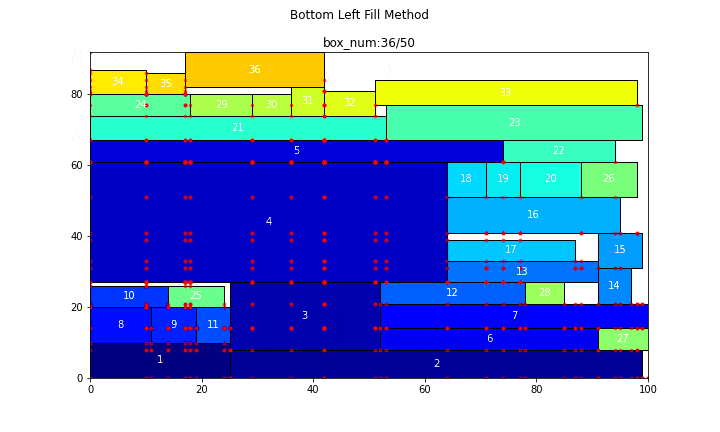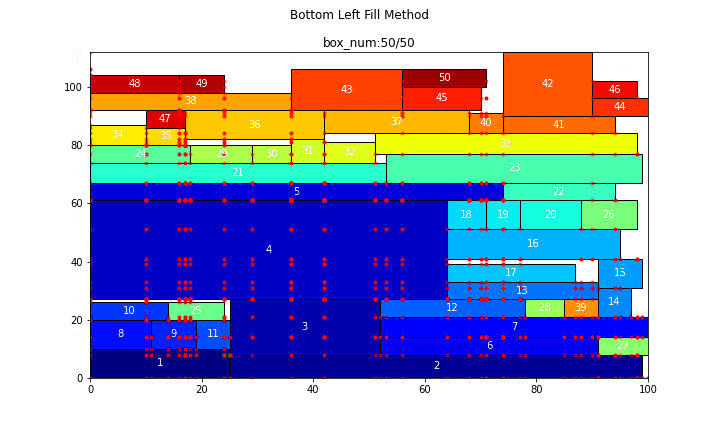
コード自体はかなり長めでしたが、やっていることそれ自体はそれなりに単純で、コメントでも書いた通り、

• BL安定点の内、最良のものを選択し、長方形を設置する
• この長方形によって生じる新たなBL安定点を追加する

ということを繰り返しているだけです。
ビジュアライズ結果から、そのことを読み取って頂けていれば幸いです。

考察

結局このBLF法は何がいいの?

恐らくですが、BLF法それ自体が非常に重要な手法かというと、そうではないと思っています。 あくまで私個人の感想ですが、少しマイナーなヒューリスティック的解法の一つと言った印象です。
ただ、だからと言ってBLF法から学べる点がないかと言うと、決してそんなことはない、と思っています。

BLF法のメタ的な部分で一番重要なことは、教科書の表現をそのまま借りると、「解空間とは異なる探索空間を導入する」という事ではないでしょうか。
長方形詰め込み問題自体の探索空間は、制約さえ満たせばすべての長方形が任意の実数値の座標をとってもいいので、無限に広がっています。

しかし、BL安定点にのみ探索空間を狭めることによって、現実的な組み合わせ数($O(n^2)$)のみの探索に帰着できるというのがBLF法の要点の一つだと思っています。

これはもっと一般の場合においても非常に重要なことです。無闇やたらに解を探し求めてもうまく行かないことは頻繁にあります。

ヒューリスティックという言葉の意味が発見的解法であることは非常に示唆深いと個人的には思っていて、適当に乱択すればそれは則ちヒューリスティックかと言えば、全くそんなことはありません。
(なお、これには大いに自戒の意が込められています。)

一般に、最適な解の構造というのが一体どのような特徴を有しているかをきちんと分析し、それを適切に今まで扱ってきた各手法(メタヒューリスティック)などに当てはめてこそ、初めて良い結果というのが得られることが多いと思っています。

この長方形詰め込み問題では、BL安定点というのが正にそれにあたっており、その特徴を利用したが故に近似的ではあるものの大分良い解を得ることが出来ているのではないでしょうか。そしてそれより一歩進んだ解を得るには、その構造から少し外れたところにある解も拾っていくが重要になってくる、とも思っています。

簡潔にまとめると、探索空間をどのように取るかは非常に重要だ、ということが要点になります。

ビジュアライズ結果についての注釈

ここで、よくよくビジュアライズ結果を観察すると、他の長方形内部に埋まってしまっていて、明らかに意味をなさないbl安定点がいくつかあることに気付きます。これは削除可能なBL安定点なのでしょうか?

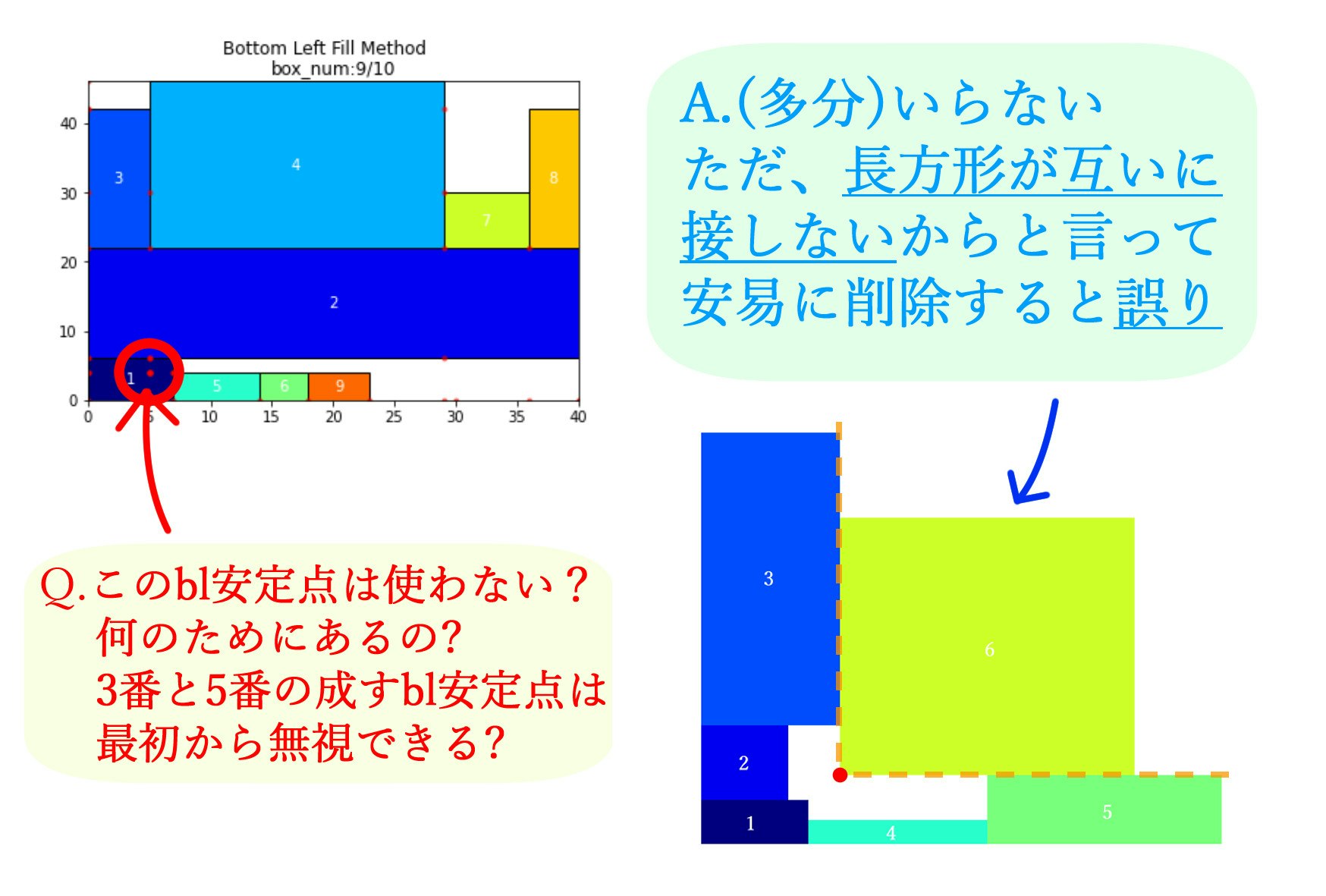
上の図に言いたいことはまとめてありますが、長方形内部に埋まっている安定点も、状況によっては長方形外にでるので、意味を成すこともあるよ、というのが言いたいことです。
(なお、上の図の右側に関してはあくまでイメージであり、厳密には少し異なります。)

既に敷き詰められた長方形はもう動かないことなどを踏まえると、これらを最初から候補に加えないといった改善も可能と思われますが、その判定は面倒であったり計算量がそこまでよくなかったりという理由の為、このまま放置されているのではないか考えています。

まとめ

• 探索空間をどう取るかは非常に大切
• BLF法は面白い!

MountainCar

最後にこの項では遺伝的アルゴリズムについて扱っていきます。
具体例として、MountainCarという問題を解いていきます。

説明

MountainCarとは?

まず、OpenAI Gymというものがあるのですが、これは機械学習の分野の一つである強化学習を、勉強・開発するためのツールキットです。
そしてここでは、その提供されているツールの一つ、MountainCarを用いて、遺伝的アルゴリズムの動作確認に利用します。

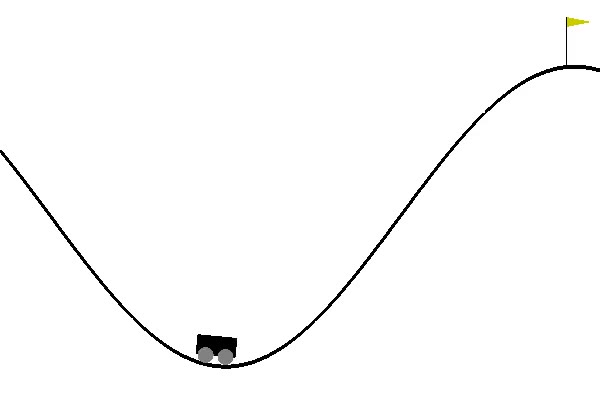
上の画像がMountainCarが与える問題を図示したものになっています。
車(🚗)に対して指示を出すことにより、ゴール(🚩)へと到達させるというのが主な目標になりますが、単に「右に進め」と指示するだけでは、車はゴールしてくれません。上手く左の斜面などを用いて助走をつける必要があります。
そして、その助走の付け方などを、上手くコンピューターに学ばせようというのが、題意になります。

以下、OpenAI Gymが提供する環境(env)について、少し意味を記します。

• Observation

Num	Observation	Min	Max
0	position	-1.2	0.6
1	velocity	-0.07	0.07

このpositionが0.5の地点にゴール(🚩)が存在しています。

• Actions

Num	Action
0	push left
1	no push
2	push right

我々が車(🚗)に対して出せる指示はこの三種類です。
これらを上手く制御することによって、車をゴールに導きます。

• Reward

ゴールに到達するまで、各ステップごとに-1されます。
左側の山に登るなどしても、特に罰則はありません。

• Starting State

-0.6から-0.4までのランダムなポジションから、初速度0でスタートします。

• Episode Termination
  ゴールに到達した時点、または200回イテレーションした時点で終了します。

参考にさせて頂いたリンク
Colab上のチュートリアル
MountainCarの公式github

遺伝的アルゴリズムとは?

大体のイメージは、以下の動画などが特に分かりやすいと思います。

具体的な手順等は後述するのでここでは省略します。

また、少し別の観点から言えば、タブーサーチと並んで学術分野よりの手法なのかなと勝手に思っています。(真偽は知りません。)

競プロ文脈で遺伝的アルゴリズムを聞くことが私はないのですが、論文を検索すると一番頻繁に目にするイメージです。実際、Google Scholarで検索をかけると、遺伝的アルゴリズムの方が焼き鈍し法などに比べ遥かにヒット件数が多いことが分かるかと思います。

実践

では、以下から実際にやっていきます。
まず、OpenAI Gymのセットアップやビジュアライザの設定をします。

セットアップ用コード

# このセルは見る必要なし

NUM_OF_TURN = 200

def query_environment(name):
  env = gym.make(name)
  spec = gym.spec(name)
  print("--------このゲームに関する情報--------")
  print(f"Action Space: {env.action_space}")
  print(f"Observation Space: {env.observation_space}")
  print(f"Max Episode Steps: {spec.max_episode_steps}")
  print(f"Nondeterministic: {spec.nondeterministic}")
  print(f"Reward Range: {env.reward_range}")
  print(f"Reward Threshold: {spec.reward_threshold}")


def show_video():
    mp4list = glob.glob('video/*.mp4')
    if len(mp4list) > 0:
        mp4 = mp4list[0]
        video = io.open(mp4, 'r+b').read()
        encoded = base64.b64encode(video)
        ipythondisplay.display(HTML(data='''<video alt="test" autoplay 
                loop controls style="height: 400px;">
                <source src="data:video/mp4;base64,{0}" type="video/mp4" />
             </video>'''.format(encoded.decode('ascii'))))
    else:
        print("Could not find video")


def wrap_env(env):
    env = Monitor(env, './video', force=True)
    return env

# 以降ではこの関数のみ用いる 副作用なし
def vis(actions:List[int]):
    assert len(actions)==NUM_OF_TURN, "NUM_OF_TURN分のactionが必要です"
    env = wrap_env(gym.make("MountainCar-v0"))
    env.reset()
    for t in range(NUM_OF_TURN):
        env.render()
        action = actions[t]
        assert action in (0,1,2), "actionは0,1,2のいずれかである必要があります"
        observation, reward, done, info = env.step(action)
        if done:
            break
    print("---RESULT---")
    if t==NUM_OF_TURN-1:
        print("NOT FINISHED")
    else:
        print("FINISHED", f"(turn: {t})")
    print("---VIDEO---")
    env.close()
    show_video()

if __name__=='__main__':
    display = Display(visible=0, size=(1400, 900))
    display.start()
    query_environment("MountainCar-v0")

実行結果

--------このゲームに関する情報--------
Action Space: Discrete(3)
Observation Space: Box(-1.2000000476837158, 0.6000000238418579, (2,), float32)
Max Episode Steps: 200
Nondeterministic: False
Reward Range: (-inf, inf)
Reward Threshold: -110.0

手始めに、乱数を使って行動を制御してみます。

vis([random.randint(0,2) for _ in range(NUM_OF_TURN)])

実行結果

    ---RESULT---
    NOT FINISHED

出力された動画を見れば分かる通り、乱数だけではどうにも動いてくれません。
これをどんどん改良していくことを目指します。

次に便宜上の関数などを定めておきます。

# このセルは見る必要なし

SIZE_OF_GROUP = 10

class Actions:
    # 各ターンの行動を一纏めにしたclass
    def __init__(self,actions:List[int]=None) -> None:
        if actions is not None:
            self.actions=actions
        else:
            self.actions=np.random.randint(0, 2, NUM_OF_TURN)
        self.score=None
        calc_score(self)

    def __getitem__(self,key):
        return self.actions[key]

    def __str__(self):
        return f"score:{self.score} actions:"+''.join(np.vectorize(str)(self.actions))

    def set_score(self,score):
        assert self.score is None and score is not None
        self.score=score

def calc_score(actions:Actions):
    score=0
    for _ in range(5):
        env = gym.make('MountainCar-v0')
        env.reset()
        total_reward = 0
        max_position = -1.2
        for t in range(NUM_OF_TURN):
            action = actions[t]
            observation, reward, done, info = env.step(action)
            total_reward += reward
            max_position = max(max_position, observation[0])
            if done:
                break
        assert -1.2<=max_position<=0.6
        score += total_reward*10+max_position
    actions.set_score(score)
    return score

def get_best_idx(group:List[Actions]):
    scores=np.vectorize(lambda x:x.score)(group)
    return np.argmax(scores)

そして、本題である遺伝的アルゴリズムの概要について、以下に示します。教科書p.300からの引用です。

遺伝的アルゴリズム

Step1. 初期集団$P$を生成する. 集団$P$の最良解を$x^♮$とする。
Step2. (交叉) 現在の集団$P$の中から2つ以上の解(親)を選び、それらを組み合わせて新たな解(子)の集合$Q_1$を生成する。
Step3. (突然変異) 現在の集団$P$から選んだ解、もしくはStep2で生成した解の集合$Q_1$から選んだ解にランダムな変形を加えて新たな解の集合$Q_2$を生成する。
Step4. 集合$P∪Q_1∪Q_2$の最良解を$x'$とする。$f(x') \leq f(x^♮)$ならば、$x^♮=x'$とする。
Step5. (選択) 集合$P∪Q_1∪Q_2$から$p$個の解候補を選び、次世代の集団$P'$とする。
Step6. 終了条件を満たせばを出力して終了、そうでなければ、$P=P'$としてStep2に戻る。

(※今回はStep6については省略し、一定回数、確定でループさせることとしました)

ここで、交叉、突然変異、選択という用語が出てきましたが、それぞれのステップを具体的にどう実装するかはGAにとって重要な要素です。

例えば、このDeguchi Labというサイトなどにもよくまとまっています。

具体的な実装としては以下の通りです。
詳細な説明については省略しますが、コメントで何となくは伝わるかと思います。

CROSSOVER_COUNT = 6
MUTATION_COUNT = 4

# 交叉
def crossover(group:List[Actions])->List[Actions]:
    # ここでは2点交叉を採用しました
    # [交叉前]
    # 適当な遺伝子を2つ選んできて、
    # parent_1    0000000000000000000000000
    # parent_2    1111111111111111111111111
    #                 ↑        ↑
    #          begin_point     end_point 2点を選び、
    # [交叉後]
    # new_gene  0000000111111111100000000
    # こういう遺伝子を新たに作る
    ret=[]
    fitness_arr = np.vectorize(lambda x:x.score)(group)
    assert np.all(fitness_arr!=np.nan)
    fitness_arr/=sum(fitness_arr)
    for _ in range(CROSSOVER_COUNT):
        parent_1,parent_2=select(group,2,fitness_arr)
        assert isinstance(parent_1,Actions)
        assert isinstance(parent_2,Actions)
        begin_point=random.randrange(NUM_OF_TURN)
        end_point=random.randrange(NUM_OF_TURN)
        if begin_point>end_point:
            begin_point,end_point=end_point,begin_point
        new_gene=parent_1.actions.copy()
        new_gene[begin_point:end_point]=parent_2.actions[begin_point: end_point]
        ret.append(Actions(new_gene))
    return np.array(ret)

# 突然変異
def mutation(group:List[Actions]):
    # ここでは区間を別の動作に置き換える突然変異を採用しました
    # [変異前]
    # 適当な遺伝子を1つ選んできて、
    # parent    0000000000000000000000000
    #                 ↑        ↑
    #          begin_point     end_point 区間を選び、
    # [変異後]
    # new_gene  0000000222222222200000000
    # 適当な数字に置き換えることによって、
    # 新たな遺伝子を作る
    ret=[]
    fitness_arr = np.vectorize(lambda x:x.score)(group)
    assert np.all(fitness_arr!=np.nan)
    fitness_arr/=sum(fitness_arr)
    for _ in range(MUTATION_COUNT):
        parent, *_ = select(group,1,fitness_arr)
        assert isinstance(parent,Actions)
        new_gene = parent.actions
        begin_point=random.randrange(NUM_OF_TURN)
        end_point=random.randrange(NUM_OF_TURN)
        new_gene[begin_point:end_point]=random.randint(0,2)
        ret.append(Actions(new_gene))
    return ret

# 選択
def select(group:List[Actions], num_of_select,fitness_arr):
    # ここではルーレット選択を採用しました
    # 非常に単純な選択方法で、適応度(fitness)が高いものほど
    # 取る確率を高くした上で、乱択するだけです
    if fitness_arr is None:
        fitness_arr = np.vectorize(lambda x:x.score)(group)
        assert np.all(fitness_arr!=np.nan)
        fitness_arr/=sum(fitness_arr)
    assert len(group)>=num_of_select
    assert abs(sum(fitness_arr)-1.0)<1e-5
    idx = np.random.choice(np.arange(len(group)),
                           size=num_of_select,
                           p=fitness_arr)
    return group[idx]

def GA(num_of_generations):
    # Step1.
    # 初期集団Pを生成する. 集団Pの最良解をx♮とする
    P = np.array([Actions() for _ in range(SIZE_OF_GROUP)])
    x_natural = P[get_best_idx(P)]
    hist=[]

    for generation_number in range(num_of_generations):
        # Step2. (交叉)
        # 現在の集団Pの中から2つ以上の解を選び、それらを組み合わせて新たな解の集合Q1を生成する
        Q1=crossover(P)
        # Step3. (突然変異)
        # 現在の集団Pから選んだ解、もしくはStep2で生成した解の集合Q1から選んだ解にランダムな変形を加えて新たな解の集合Q2を生成する
        Q2=mutation(np.concatenate((P,Q1)))
        # Step4. 
        # 集合$P∪Q1∪Q2$の最良解をx'とする f(x') <= f(x^♮)ならば、x^♮=x'とする
        P_Q1_Q2=np.concatenate((P,Q1,Q2))
        x_dash=P_Q1_Q2[get_best_idx(P_Q1_Q2)]
        if x_dash.score>=x_natural.score:
            x_natural=x_dash
        hist.append(x_natural.actions.copy())
        # Step5. (選択)
        # 集合P∪Q1∪Q2からp個の解候補を選び、次世代の集団P'とする
        P = select(P_Q1_Q2, SIZE_OF_GROUP, None)
        if generation_number%10==0:
            print(f"----------{generation_number}世代目----------")
            print(f"現在の最良遺伝子: {x_natural}")
    
    print("\n終了!")
    
    return hist

結果

hist=GA(200)

実行結果

----------0世代目----------
現在の最良遺伝子: score:-10000.157370157032 actions:11001111010100001001110011101101101000000011001110011101001010111111011011101110110000101011110110011001011011111022222222222222222222222222222222222222222000000001011010001100100001000001000100111111
----------10世代目----------
現在の最良遺伝子: score:-7807.358975035118 actions:00000011110010001110001000100110000022222222222222222222220000000000000111111000111010001110000100110010001011101000022222222222222222222222222222222222222222222222222222222222220001101100000100010100
----------20世代目----------
現在の最良遺伝子: score:-7317.420223098776 actions:00000011110010001110001000100110022222222222222222222220000000000000000000000000000000000000000000000000000000022222222222222222222222222222222011111111111111111111111111111111111111111111100100010100
----------30世代目----------
現在の最良遺伝子: score:-7317.420223098776 actions:00000011110010001110001000100110022222222222222222222220000000000000000000000000000000000000000000000000000000022222222222222222222222222222222011111111111111111111111111111111111111111111100100010100
----------40世代目----------
現在の最良遺伝子: score:-6837.36973446727 actions:00000011110010000000000002222222222222222222222220000000000000000000000000000000000000000002222222222222222222222222222222022222222222222222222222222222000000000000000011111111120001101100100100010100
----------50世代目----------
現在の最良遺伝子: score:-6837.36973446727 actions:00000011110010000000000002222222222222222222222220000000000000000000000000000000000000000002222222222222222222222222222222022222222222222222222222222222000000000000000011111111120001101100100100010100
----------60世代目----------
現在の最良遺伝子: score:-6187.441425044063 actions:00000011111111222222222222222222222220000000000000000000000000000000222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222010100
----------70世代目----------
現在の最良遺伝子: score:-6187.441425044063 actions:00000011111111222222222222222222222220000000000000000000000000000000222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222010100
----------80世代目----------
現在の最良遺伝子: score:-6187.441425044063 actions:00000011111111222222222222222222222220000000000000000000000000000000222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222010100
----------90世代目----------
現在の最良遺伝子: score:-5897.447490402048 actions:00222222222222222222222222222222222221110000000000000000000000000002222222111111112222222222222222222222222222222222222222222222222222222211111111111111112222211111110011111111120222222222222222222200
----------100世代目----------
現在の最良遺伝子: score:-5897.447490402048 actions:00222222222222222222222222222222222221110000000000000000000000000002222222111111112222222222222222222222222222222222222222222222222222222211111111111111112222211111110011111111120222222222222222222200
----------110世代目----------
現在の最良遺伝子: score:-5677.8286702033965 actions:00000000000000000000000000000000000000000022222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222220000000000000000002222222222200
----------120世代目----------
現在の最良遺伝子: score:-5677.8286702033965 actions:00000000000000000000000000000000000000000022222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222220000000000000000002222222222200
----------130世代目----------
現在の最良遺伝子: score:-5677.8286702033965 actions:00000000000000000000000000000000000000000022222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222220000000000000000002222222222200
----------140世代目----------
現在の最良遺伝子: score:-5677.8286702033965 actions:00000000000000000000000000000000000000000022222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222220000000000000000002222222222200
----------150世代目----------
現在の最良遺伝子: score:-5677.8286702033965 actions:00000000000000000000000000000000000000000022222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222220000000000000000002222222222200
----------160世代目----------
現在の最良遺伝子: score:-5677.8286702033965 actions:00000000000000000000000000000000000000000022222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222220000000000000000002222222222200
----------170世代目----------
現在の最良遺伝子: score:-5677.8286702033965 actions:00000000000000000000000000000000000000000022222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222220000000000000000002222222222200
----------180世代目----------
現在の最良遺伝子: score:-5677.8286702033965 actions:00000000000000000000000000000000000000000022222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222220000000000000000002222222222200
----------190世代目----------
現在の最良遺伝子: score:-5677.8286702033965 actions:00000000000000000000000000000000000000000022222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222220000000000000000002222222222200

終了!

[第1世代]
一応少し高いところまではいくが、まだどうすればいいのかあまり分かってなさそう。

vis(hist[0])

実行結果

---RESULT---
NOT FINISHED

[第40世代]
各世代での試行錯誤の成果として、きちんとゴールしてくれる動作を示すようになる。 ただ、少し動作に無駄があるようにも思える。

vis(hist[40])

実行結果

---RESULT---
FINISHED (turn: 137)

[第80世代]
大分洗練された動きを示すようになる。助走の付け方も合理的に。

vis(hist[80])

実行結果

---RESULT---
FINISHED (turn: 121)

[最終世代]
最も早くゴールに到達してくれるようになった。 何回か学習を繰り返してみましたが、これが一番良い答えのようです。

vis(hist[-1])

実行結果

---RESULT---
FINISHED (turn: 90)

以下に、どのような学習過程を得て、この動きを得たのか視覚化してみます。

学習履歴表示用コード

# 学習履歴の表示
cmap = ListedColormap(['#F0F788', '#F0F0F0', '#9DA2F8'], name="custom")
xticks = [i for i in range(0, NUM_OF_TURN+1, 10)]
xticklabels = list(map(str, range(0, NUM_OF_TURN+1, 10)))
yticks = [len(hist)-i for i in range(0, len(hist)+1, 10)]
yticklabels = list(map(str, range(0, len(hist)+1, 10)))
fig = plt.figure(figsize=(20, 7))
spec = gridspec.GridSpec(ncols=2, nrows=1, width_ratios=[10, 1])
ax1 = fig.add_subplot(spec[0, 0],
                      xticks=xticks, xticklabels=xticklabels,
                      yticks=yticks, yticklabels=yticklabels)
ax1.set_title("Learning History of Genetic Algorithms", fontsize=20)
ax1.set_xlabel("num of turn", fontsize=15)
ax1.set_ylabel("generation", fontsize=15)
ax1.pcolormesh(hist[::-1], cmap=cmap)
ax2 = fig.add_subplot(spec[0, 1], xticks=[], yticks=[])
ax2.pcolormesh([[2], [1], [0]], cmap=cmap)
ax2.text(0.5, 2.5, "0 (LEFT)", ha='center', va='center', fontsize=15)
ax2.text(0.5, 1.5, "1 (STAY)", ha='center', va='center', fontsize=15)
ax2.text(0.5, 0.5, "2 (RIGHT)", ha='center', va='center', fontsize=15)
plt.tight_layout()
plt.show()

図にも書きましたが、黄色がLEFT,灰色がSTAY,青色がRIGHTを示していて、横軸がターン数、縦軸が世代になっています。(下に行くほど、進化した世代となっています)
最後の方の世代では、ある一定ターン以降は既にゴール済みの為、意味のあるactionにはなっていないことに注意してください。

その上で、このグラフを観察すると、世代を重ねるごとに動作が洗練されていくことや、途中でかなり大きな突然変異が起きていること、最後の方は淘汰がほぼ完全になされたのか変化がないことが確認できると思います。

ところで、交叉や選択に関しては、様々なバリエーションがあると先述しましたが、それらを変えた場合はどのような挙動を示すようになるのでしょうか。
ここでは、突然変異を以下のように変えてみました。

# 突然変異
def mutation(group:List[Actions]):
    # ここでは区間を別の動作に「個別に」置き換える突然変異を採用しました
    # 先程までの突然変異では、区間をある特定の別の動作(つまり一種類のみ)に置き換えていました
    # [変異前]
    # 適当な遺伝子を1つ選んできて、
    # parent    0000000000000000000000000
    #                 ↑        ↑
    #          begin_point     end_point 区間を選び、
    # [変異後]
    # new_gene  0000000201012001200000000
    # 適当な数字に置き換えることによって、
    # 新たな遺伝子を作る
    ret=[]
    fitness_arr = np.vectorize(lambda x:x.score)(group)
    assert np.all(fitness_arr!=np.nan)
    fitness_arr /= sum(fitness_arr)
    for _ in range(MUTATION_COUNT):
        parent, *_ = select(group,1,fitness_arr)
        assert isinstance(parent,Actions)
        new_gene = parent.actions
        begin_point = random.randrange(NUM_OF_TURN)
        end_point = random.randrange(NUM_OF_TURN)
        for i in range(begin_point, end_point):
            new_gene[i] = random.randint(0,2)
        ret.append(Actions(new_gene))
    return ret

def GA(num_of_generations):
    # Step1.
    # 初期集団Pを生成する. 集団Pの最良解をx♮とする。
    P = np.array([Actions() for _ in range(SIZE_OF_GROUP)])
    x_natural = P[get_best_idx(P)]
    hist=[]

    for generation_number in range(num_of_generations):
        # Step2. (交叉)
        # 現在の集団Pの中から2つ以上の解を選び、それらを組み合わせて新たな解の集合Q1を生成する。
        Q1=crossover(P)
        # Step3. (突然変異)
        # 現在の集団Pから選んだ解、もしくはStep2で生成した解の集合Q1から選んだ解にランダムな変形を加えて新たな解の集合Q2を生成する。
        Q2=mutation(np.concatenate((P,Q1)))
        # Step4. 
        # 集合$P∪Q1∪Q2$の最良解をx'とする。f(x') <= f(x^♮)ならば、x^♮=x'とする。  
        P_Q1_Q2=np.concatenate((P,Q1,Q2))
        x_dash=P_Q1_Q2[get_best_idx(P_Q1_Q2)]
        if x_dash.score>=x_natural.score: # 逆向き
            x_natural=x_dash
        hist.append(x_natural.actions.copy())
        # Step5. (選択)
        # 集合P∪Q1∪Q2からp個の解候補を選び、次世代の集団P'とする。
        P = select(P_Q1_Q2, SIZE_OF_GROUP, None)
        if generation_number%10==0:
            print(f"----------{generation_number}世代目----------")
            print(f"現在の最良遺伝子: {x_natural}")
    
    print("\n終了!")
    
    return hist

以下が、このような再定義をした場合の実行結果です。

hist=GA(100)

実行結果

----------0世代目----------
現在の最良遺伝子: score:-10001.768748979146 actions:00001010110111011101110111100101012112000110201011001012001021021112121110002200011100200102122000222011221222220122022120002211221021102020121022212002122022222212011222000120010001110001011010011100
----------10世代目----------
現在の最良遺伝子: score:-10001.280594496297 actions:10101011100000000111210000201000020221201211210022001202020202110210002220212110200010120122122020022002121110002222201012101200202001012021222222002121010000110122012110120020112011011101010111010001
----------20世代目----------
現在の最良遺伝子: score:-10001.113059408404 actions:10101011100000000111100001021010221210210101010200111010110221211212221000211111000100112121100010102111020010011001100011100110011220222010211221022122011001001021221220100001110012220021100022110001
----------30世代目----------
現在の最良遺伝子: score:-10001.113059408404 actions:10101011100000000111100001021010221210210101010200111010110221211212221000211111000100112121100010102111020010011001100011100110011220222010211221022122011001001021221220100001110012220021100022110001
----------40世代目----------
現在の最良遺伝子: score:-10001.113059408404 actions:10101011100000000111100001021010221210210101010200111010110221211212221000211111000100112121100010102111020010011001100011100110011220222010211221022122011001001021221220100001110012220021100022110001
----------50世代目----------
現在の最良遺伝子: score:-10001.113059408404 actions:10101011100000000111100001021010221210210101010200111010110221211212221000211111000100112121100010102111020010011001100011100110011220222010211221022122011001001021221220100001110012220021100022110001
----------60世代目----------
現在の最良遺伝子: score:-10001.113059408404 actions:10101011100000000111100001021010221210210101010200111010110221211212221000211111000100112121100010102111020010011001100011100110011220222010211221022122011001001021221220100001110012220021100022110001
----------70世代目----------
現在の最良遺伝子: score:-10001.113059408404 actions:10101011100000000111100001021010221210210101010200111010110221211212221000211111000100112121100010102111020010011001100011100110011220222010211221022122011001001021221220100001110012220021100022110001
----------80世代目----------
現在の最良遺伝子: score:-10001.113059408404 actions:10101011100000000111100001021010221210210101010200111010110221211212221000211111000100112121100010102111020010011001100011100110011220222010211221022122011001001021221220100001110012220021100022110001
----------90世代目----------
現在の最良遺伝子: score:-10001.113059408404 actions:10101011100000000111100001021010221210210101010200111010110221211212221000211111000100112121100010102111020010011001100011100110011220222010211221022122011001001021221220100001110012220021100022110001

終了!

スコアの部分に注目して頂きたいのですが、誤差レベルでしか改善していません。つまり、このような突然変異では駄目だという結果になりました。
他の局所探索法と同様に、ある程度問題に対する考察をした上で、適切な近傍を設計することが大切だということがよく分かります。

感想

以下は個人的感想です。

私はGAにそこまで詳しい訳ではなかったのですが、案外本質はこれまでやってきたヒューリスティックの技法と似ているな、と言うことを強く感じました。
OpenAI Gymの問題は、一般的には方策勾配法やQ学習等で解かれる印象があるのですが、それら強化学習系の手法と比べても、確かに局所探索法よりの手法なんだなと思います。

例えば、一番最初に扱った局所探索法との対応で言えば、

• GAの交叉が局所探索法のPOPに基づく近傍の生成に、
• GAの突然変異が局所探索法のキックに、
• GAの選択が山登り法や焼き鈍し法などの遷移式に、

それぞれ似ていると感じています。
こういった類似性が見られるのは、メタヒューリスティックの面白い点の一つかもしれません。

また、強化学習よりの手法なので、少し計算コストが高めのように感じられますが、特に事前計算が出来るような場合には非常に効果を発揮するのではないかと思っています。

最後に

いかがでしたでしょうか。

本ノートブックでは紹介出来ていない内容も沢山あるので、教科書も是非ご覧ください。例えば、教科書の最後の方に記されている劣勾配法やラグランジュヒューリスティック等には触れていません。(場合によっては追記します。)

ヒューリスティックの楽しさ、奥深さが少しでも伝わっていれば嬉しい限りです。
ありがとうございました。

参考資料

threecourseさんによる、参考にサイトをまとめたサイト (ここに載っているサイトはほぼ全て参考にさせて頂きました)

tanaka-aさんによる、AtCoder上のヒューリスティックコンテストについて非常にまとまった素晴らしい記事

TERRRYさんによる、特に短期AHCが好きな方に非常にお勧めしたい記事

また、その他多くの方々によるコンテスト参加記なども参考にさせて頂きました。
この場を借りてお礼申し上げます。

そして最後に、梅谷俊治先生の「しっかり学ぶ数理最適化 モデルからアルゴリズムまで」
という本を紹介させて頂き、本記事を締めさせて頂きます。
ここまでお読みいただきありがとうございました。