競プロ解法紹介～レベル別マラソンの戦い方～

2018年02月18日（8時間）に開かれたマラソン形式の競技プログラミングコンテスト、Hack To The Future 予選問題について、マラソン初心者からマラソンイエローコーダー以下までのレベル別の戦い方紹介です。

問題概要「 山型足し算」※原文引用

N 行 N 列のマス目 A が与えられます。一番左上のマスの位置を (0,0) と定義します。
このとき、左上のマスから下に i (0≦i≦N−1) マス、右に j (0≦j≦N−1) マス進んだマスの位置は (j,i) で表されます。
また，各マスに整数が書かれており、位置 (j,i) のマスに書かれている整数を Ai,j で表します。

ここで、マス目に対して全てのマスに書かれている整数が 0 である状態を「初期マス目」と定義します。
また、マス目 P に対する「山型足し算」 (X,Y,H) を以下のように定義します。

• まず，山の中心となるマスの位置 (X,Y) (0≦X,Y≦N−1) と山の高さを表す整数 H (1≦H≦N) を指定します。
• その後、全てのマスの Py,x を Py,x+max(0,H−|x−X|−|y−Y|) に書き換えます。

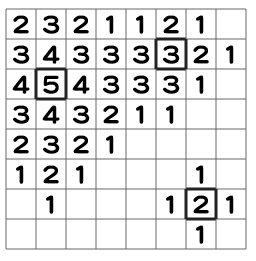
例として、8 行 8 列の初期マス目であるマス目 Q を考えます。
マス目 Q に対して、 3 回の山型足し算 (X,Y,H)=(1,2,5),(5,1,3),(6,6,2) を行った後のマス目を以下の図に示します。

図 山型足し算の例 (空白のマスは 0 を表す。)

与えられたマス目 A は、N 行 N 列の初期マス目に対して、山型足し算を 1000 回行って生成されたマス目です。
あなたの目的は、マス目 A にできる限り近いマス目を生成する山型足し算の手順を求めることです。

具体的にはまず、N 行 N 列の初期マス目であるマス目 B を用意します。
次に、あなたはマス目 B に対して山型足し算を最大 1000 回まで行うことができます。
そして、マス目 A とマス目 B を比較したとき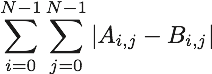を最小化する山型足し算の手順を求めることを目的とします。
さらに、マス目 A を生成するような山型足し算の手順が複数存在する場合には、山型足し算の回数を最小化することを目指してください。

解法

では解いていきましょう。マラソンでは、アルゴ形式のコーナーケースまで上手く対処し厳密解を求め、を取るアプローチとは違った考えが必要です。

有効な回答（AC）を取る

まずは入出力チェックも兼ねて、最低限の出力でACを取りにいきます。（マラソンでは入出力形式さえ合っていればACとなります。）
今回は「0」を出力するだけですね。

Main.java

import java.io.IOException;
import java.util.Scanner;

/**
 * Hack To The Future 2018
 *
 * @author tsukammo
 */
public class Main {

	Scanner sc = new Scanner(System.in);

	public static void main(String[] args) throws IOException {
		new Main().solve();
	}

	// 制約
	final static int N = 100, row = 100, col = 100, pnum = 1000;

	void solve() {
		input();
		output();
	}

	int[][] map = new int[row][col];

	void input() {
		for (int i = 0; i < row; i++) {
			for (int j = 0; j < col; j++) {
				map[j][i] = sc.nextInt();
			}
		}
	}

	void output() {
		// ACを取る
		System.out.println(0);
	}
}

上記を提出すると、4,625,945,259点でした。ここから点数を伸ばしていきます。（結果詳細）

マラソン初心者の戦い方

普段競技プログラミングはアルゴ形式しか出たことがなく、マラソン形式は初めてor経験が浅いという方を対象として説明します。
大前提として、厳密解が求められないことを確認した上で、最適解をどうやって求めていけばよいか考えていきます。（時々厳密解が求まる問題もあります。計算量の確認はお忘れなく。）

テストケースの偏りを確認する

手組みでコーナーケース等を用意するアルゴ形式とは大きく違い、マラソン形式のテストケースは、その作成方法が明示されていることが多いです。これは、ルールは同じでもテストケースの偏りに応じて有効な回答も変わってくるためです。
今回のテストケースの生成方法は下記です。※原文引用

マス目 A は初期マス目に対して、1000 回の山型足し算を行うことで生成される。
各回の山型足し算で用いられるパラメータ (X,Y,H) についての制約

• X は [0,N−1] の範囲で、一様乱数によってランダムに選ばれる。
• Y は [0,N−1] の範囲で、一様乱数によってランダムに選ばれる。
• H は [1,N] の範囲で、一様乱数によってランダムに選ばれる。

完全な乱択を1,000回実施しているようです。乱択を複数回実行しているため、個々の山の差異が吸収され、全体的に下記のような姿に近づくことが想像できます。

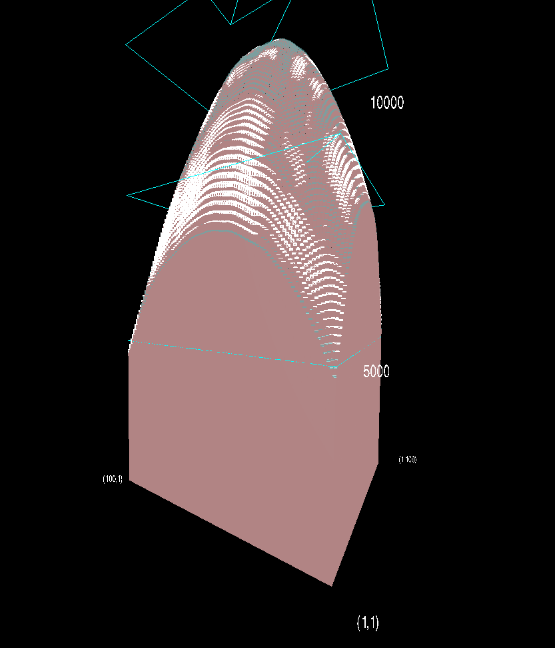
図 ビジュアライザよりテストケース「example_01」（高さは1/100に縮小）

個々の山の差異が吸収されるのであれば、テストケース作成と同様の方法で乱択で回答を作ってしまいましょう。

Main.java

（省略）

public class Main {

	（省略）

	void solve() {
		input();
		init(); // new
		output();
	}

	Random rnd = new Random(20180217);
	int[][] ans = new int[1000][3];

	void init() {
		for (int i = 0; i < pnum; i++) {
			int x = rnd.nextInt(100);
			int y = rnd.nextInt(100);
			int h = rnd.nextInt(100) + 1;
			ans[i][0] = x;
			ans[i][1] = y;
			ans[i][2] = h;
		}
	}

	（省略）
	
	// update
	void output() {
		// 乱択した山を出力する
		System.out.println(ans.length);
		for (int i = 0; i < ans.length; i++) {
			System.out.println(ans[i][0] + " " + ans[i][1] + " " + ans[i][2]);
		}
	}
}

上記を提出すると、9,686,819,273点でした。無闇に貪欲法を試すより楽に良い点数になるはずです。（結果詳細）

Next Step

残りのコンテスト時間で、ここからスコアを伸ばす方法を考えます。Randomのseed値を弄ったり、取りうる値の範囲を変えてみたり、といったパラメータ調整に入るのも良いですが、例えば下記の工夫は汎用的に使えるのではないでしょうか。

Main.java

（省略）

public class Main {

	（省略）

	void solve() {
		input();
		init();
		simulate(); // new
		output();
	}


	static final long timeLimit = 5500;

	void simulate() {
		long st = System.currentTimeMillis();
		long et = st + timeLimit;

		int bestScore = eval(ans);
		int[][] bestOutput = new int[1000][3];
		for (int i = 0; i < bestOutput.length; i++) {
			bestOutput[i] = Arrays.copyOf(ans[i], ans[i].length);
		}
		while (System.currentTimeMillis() < et) {
			int[][] tmpOutput = new int[1000][3];
			for (int i = 0; i < pnum; i++) {
				int x = rnd.nextInt(100);
				int y = rnd.nextInt(100);
				int h = rnd.nextInt(100) + 1;
				tmpOutput[i][0] = x;
				tmpOutput[i][1] = y;
				tmpOutput[i][2] = h;
			}
			int tmpScore = eval(tmpOutput);
			if(bestScore > tmpScore){
				bestScore = tmpScore;
				for (int i = 0; i < bestOutput.length; i++) {
					bestOutput[i] = Arrays.copyOf(tmpOutput[i], tmpOutput[i].length);
				}
			}
		}
		for (int i = 0; i < bestOutput.length; i++) {
			ans[i] = Arrays.copyOf(bestOutput[i], bestOutput[i].length);
		}
	}

	// 山の外周に沿って斜め移動
	final static int dx[] = new int[] { 1, -1, -1, 1 };
	final static int dy[] = new int[] { 1, 1, -1, -1 };

	// シミュレータ
	int eval(int[][] output) {
		int ret = 0;
		int[][] ansMap = new int[row][col];

		for (int i = 0; i < output.length; i++) {
			int x = output[i][0];
			int y = output[i][1];
			int h = output[i][2];
			ansMap[x][y] += h;
			for (int plus = 1; plus < h; plus++) {
				int d = h - plus;
				x = output[i][0];
				y = output[i][1] - d;
				for (int j = 0; j < dx.length; j++) {
					for (int k = 0; k < d; k++) {
						x = x + dx[j];
						y = y + dy[j];
						if (outMap(x, y)) {
							continue;
						}
						ansMap[x][y] += plus;
					}
				}
			}
		}

		for (int i = 0; i < row; i++) {
			for (int j = 0; j < col; j++) {
				ret += Math.abs(map[i][j] - ansMap[i][j]);
			}
		}
		return ret;
	}

	boolean outMap(int x, int y) {
		return !(x > -1 && y > -1 && x < row && y < col);
	}

	（省略）
	
	// update
	void output() {
		// 乱択した山を出力する
		System.out.println(ans.length);
		for (int i = 0; i < ans.length; i++) {
			System.out.println(ans[i][0] + " " + ans[i][1] + " " + ans[i][2]);
		}
	}
}

いきなり実装量が増えてしまいましたが、やっていることはアルゴ経験者には難しくないと思います。詰まるところ、ちゃんとシミュレータ作ってスコア計算し、制限時間いっぱい1,000個のランダムな山を生成して、一番良かったものを出力します。
上記を提出して、9,769,240,193点です。（結果詳細）

マラソン形式（最適化系の問題）が未経験の初心者の方は、この点数が目安となると思います。

マラソン経験者の戦い方

前述の内容を脳内で済ませられる方は、マラソン経験者（もしくはそれに準ずる方）と呼べると思います。
一方、「記載の内容は思いつかたなかったけど、ゴリゴリと実装した貪欲解法でもっと上の点数は取れたぜ。」という方は、少し立ち戻ってみた方が良いかもしれません。（考えた上で貪欲を採択したというのであれば問題ないです。）

では、「マラソン初心者の戦い方」のNext Stepの方法から話を進めます。
先の方法では、全部の山を作り直しているため、相当運が良くない限り良い点数はでません。一度に全部の山を作り直すのが駄目ならば、ちょっとずつ作り直していけばよいのです。

Main.java

（省略）

public class Main {

	（省略）

	void simulate() {
		long st = System.currentTimeMillis();
		long et = st + timeLimit;

		int bestScore = eval(ans);
		int[][] bestOutput = new int[1000][3];
		for (int i = 0; i < bestOutput.length; i++) {
			bestOutput[i] = Arrays.copyOf(ans[i], ans[i].length);
		}

		int loopCount = 0;
		while (System.currentTimeMillis() < et) {
			loopCount++;
			int[] tmpOutput = new int[3];
			int[] beforeOutput = new int[3];
			
			// ある山をひとつだけ選ぶ
			int n = rnd.nextInt(1000);
			beforeOutput[0] = bestOutput[n][0];
			beforeOutput[1] = bestOutput[n][1];
			beforeOutput[2] = bestOutput[n][2];

			int x = rnd.nextInt(100);
			int y = rnd.nextInt(100);
			int h = rnd.nextInt(100) + 1;
			tmpOutput[0] = x;
			tmpOutput[1] = y;
			tmpOutput[2] = h;

			bestOutput[n] = tmpOutput;
			int tmpScore = eval(bestOutput);
			if (bestScore > tmpScore) {
				bestScore = tmpScore;
			} else {
				// rollback
				bestOutput[n] = beforeOutput;
			}
		}
		System.err.println("loop:" + loopCount);
		for (int i = 0; i < bestOutput.length; i++) {
			ans[i] = Arrays.copyOf(bestOutput[i], bestOutput[i].length);
		}
	}

	（省略）
}

ある山をひとつ選んで、その山だけ作り直すプログラムです。
上記で、9,943,487,628点となります。99（ダブルナイン）に届きました。（結果詳細）

実は、このプログラムは「山登り法」になっています。
「ある状態からちょっとだけ変えて、より良くなったら採用する。」というものです。
そして、乱択のプログラムなので、高速化するだけで試行回数が上がるためまだまだ点数は伸びます。

高速化について

まず、先のプログラムの現在の試行回数を調べてみましょう。
AtCoderでは、コードテストを使うことでサーバー上での試行回数を確認できます。（ローカルPCとサーバPCのスペック差から試行回数には差異が生じます。サーバーの動作確認が可能であればやっておきましょう。）先のプログラムに、試行回数を標準エラーに出力する機能を入れているので、そのままテストしてみます。
結果は313回。ここから、ガンガン高速化して試行回数を上げていきます。

本記事では、高速化のアプローチ自体については触れません。
一般的に、山登り法（焼きなまし法）で高速化のポイントとして上がる箇所のみ扱います。

スコア計算（シミュレータ）
最も重たくなりがちなのが、スコア計算（シミュレータ）部分です。
先のプログラムは一から全て計算しているため、無駄が多くなっています。変えた部分だけ、差分計算するように改修します。

Main.java

（省略）

public class Main {

	（省略）

	void simulate() {
		long st = System.currentTimeMillis();
		long et = st + timeLimit;

		int[][] bestOutput = new int[1000][3];

		for (int i = 0; i < bestOutput.length; i++) {
			bestOutput[i] = Arrays.copyOf(ans[i], ans[i].length);
		}

		int[][] diff = makeDiff(bestOutput);
		int bestScore = 0;
		for (int i = 0; i < row; i++) {
			for (int j = 0; j < col; j++) {
				bestScore += Math.abs(diff[i][j]);
			}
		}

		int loopCount = 0;
		while (System.currentTimeMillis() < et) {
			loopCount++;
			int[] tmpOutput = new int[3];
			int[] beforeOutput = new int[3];
			int n = rnd.nextInt(1000);
			beforeOutput[0] = bestOutput[n][0];
			beforeOutput[1] = bestOutput[n][1];
			beforeOutput[2] = bestOutput[n][2];

			int x = rnd.nextInt(100);
			int y = rnd.nextInt(100);
			int h = rnd.nextInt(100) + 1;
			tmpOutput[0] = x;
			tmpOutput[1] = y;
			tmpOutput[2] = h;

			updateDiff(diff, beforeOutput, tmpOutput);
			int tmpScore = 0;
			for (int i = 0; i < row; i++) {
				for (int j = 0; j < col; j++) {
					tmpScore += Math.abs(diff[i][j]);
				}
			}

			if (bestScore > tmpScore) {
				bestScore = tmpScore;
				bestOutput[n] = tmpOutput;
			} else {
				// rollback
				updateDiff(diff, tmpOutput, beforeOutput);
			}
		}
		System.err.println("loop:" + loopCount);
		for (int i = 0; i < bestOutput.length; i++) {
			ans[i] = Arrays.copyOf(bestOutput[i], bestOutput[i].length);
		}
	}

	// 差分更新（シャローコピーのため）
	void updateDiff(int[][] diff, int[] before, int[] after) {

		// subtract
		int x = before[0];
		int y = before[1];
		int h = before[2];
		diff[x][y] += h;
		for (int plus = 1; plus < h; plus++) {
			int d = h - plus;
			x = before[0];
			y = before[1] - d;
			for (int j = 0; j < dx.length; j++) {
				for (int k = 0; k < d; k++) {
					x = x + dx[j];
					y = y + dy[j];
					if (outMap(x, y)) {
						continue;
					}
					diff[x][y] += plus;
				}
			}
		}

		// add
		x = after[0];
		y = after[1];
		h = after[2];
		diff[x][y] -= h;
		for (int plus = 1; plus < h; plus++) {
			int d = h - plus;
			x = after[0];
			y = after[1] - d;
			for (int j = 0; j < dx.length; j++) {
				for (int k = 0; k < d; k++) {
					x = x + dx[j];
					y = y + dy[j];
					if (outMap(x, y)) {
						continue;
					}
					diff[x][y] -= plus;
				}
			}
		}
	}

	int[][] makeDiff(int[][] output) {
		int[][] ret = new int[row][col];
		int[][] ansMap = new int[row][col];

		for (int i = 0; i < output.length; i++) {
			int x = output[i][0];
			int y = output[i][1];
			int h = output[i][2];
			ansMap[x][y] += h;
			for (int plus = 1; plus < h; plus++) {
				int d = h - plus;
				x = output[i][0];
				y = output[i][1] - d;
				for (int j = 0; j < dx.length; j++) {
					for (int k = 0; k < d; k++) {
						x = x + dx[j];
						y = y + dy[j];
						if (outMap(x, y)) {
							continue;
						}
						ansMap[x][y] += plus;
					}
				}
			}
		}

		for (int i = 0; i < row; i++) {
			for (int j = 0; j < col; j++) {
				ret[i][j] = map[i][j] - ansMap[i][j];
			}
		}
		return ret;
	}

	（省略）
}

ではこれの試行回数をチェックします。結果は50,941回。100倍以上高速化できました。

早速提出してみると、9,990,842,862点、999（スリーナイン）に乗りました！うひょー！（結果詳細）
このプログラムはまだまだ高速化の余地はあり、ここから更に10倍以上速くできると思います。
実際にはやりませんが、高速化を詰めばコンテスト時の2p目（40位以内）には乗れると踏んでいます。

乱択方法（近傍の選び方）について

乱択アプローチにおいて、次に取り得る状態を「近傍」と呼びます。近傍は、できるだけスコアがよくなる可能性が高いものを選びたいものです。多くの問題において、現在の状態から少しだけ変えた状態がスコア更新の可能性が高いことが知られており、近傍の範囲を狭めることで点数の向上が見込めます。

近傍を少しだけ変えたものに限定するという話は、近傍の選択肢を狭めることになるためか直感に反する方が多いようです。ここでは、より期待値の高いものに集中投資すると考えると良いかもしれません。
例：確率1%で10点取れるもの（期待値：0.1）より、確率20%で1点取れるもの（期待値：0.2）を選ぶ。

さて、現在のプログラムでは、ある山をひとつ選んでそれを作り直すという動きをします。もっと変化を小さくできないでしょうか？できます。

Main.java

（省略）

public class Main {

	（省略）

	void simulate() {
		（省略）
		while (System.currentTimeMillis() < et) {
			loopCount++;
			int[] tmpOutput = new int[3];
			int[] beforeOutput = new int[3];
			int n = rnd.nextInt(1000);
			beforeOutput[0] = bestOutput[n][0];
			beforeOutput[1] = bestOutput[n][1];
			beforeOutput[2] = bestOutput[n][2];

			// updateここから
			int x = Math.min(99, Math.max(0, beforeOutput[0] + rnd.nextInt(3) - 1));
			int y = Math.min(99, Math.max(0, beforeOutput[1] + rnd.nextInt(3) - 1));
			int h = Math.min(100, Math.max(1, beforeOutput[2] + rnd.nextInt(3) - 1));
			// updateここまで
			tmpOutput[0] = x;
			tmpOutput[1] = y;
			tmpOutput[2] = h;

			updateDiff(diff, beforeOutput, tmpOutput);
			int tmpScore = 0;
			for (int i = 0; i < row; i++) {
				for (int j = 0; j < col; j++) {
					tmpScore += Math.abs(diff[i][j]);
				}
			}

			if (bestScore > tmpScore) {
				bestScore = tmpScore;
				bestOutput[n] = tmpOutput;
			} else {
				// rollback
				updateDiff(diff, tmpOutput, beforeOutput);
			}
		}
		（省略）		
	}
	（省略）
}

x,y,hのそれぞれの変化を[-1, 0 ,+1]の範囲に絞りました。提出すると、9,997,667,119点。コンテスト時の1ページ目に乗る点数です。（結果詳細）

ここでは、山登り法について取り上げましたが、山登り法にも得意/不得意があります。
「マラソン初心者の戦い方」で考察した乱択の有効性が確認できているからこそ、今回の問題に有効なアルゴリズムとなっています。
ここらへんはアルゴ形式も同様だと思います。先にやりたいことがあって、そのために適切なアルゴリズムを選びましょう。

Next Step

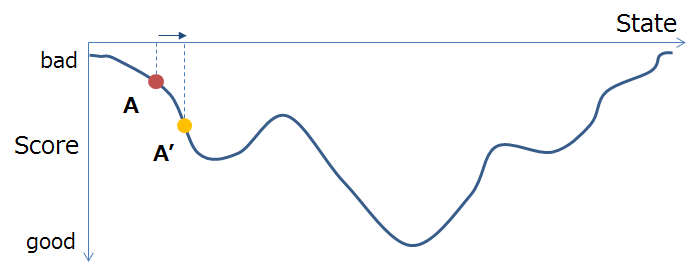
山登り法が有効な問題では、是非試しましょう「焼きなまし法」。※焼きなまし法自体の説明は他の素晴らしい記事をご覧下さい。
山登り法は、必ずスコアが良くなる方向にしか更新されず、局所解に陥りやすいという欠点があります。焼きなまし法では、条件を満たす場合はスコアが悪くなる方向にも更新を許すことで、その欠点を克服しようとするアルゴリズムです。条件設定の仕方や温度管理と呼ばれるパラメータ調整等の要素があり、かなり奥の深いアルゴリズムです。
今回は、焼きなまし法を使いこなすことが目的ではないので、私の愛用している確率オンリーの許容条件設定による解法を紹介します。

Main.java

（省略）

public class Main {

	（省略）

	void simulate() {
		（省略）

		// update ここから
		long currentTime = System.currentTimeMillis();
		double C = timeLimit * 100;		// 許容する確率定数。適当に弄る。
		double forceLine;			// 許容ライン。時間経過によりラインを厳しくしていく。
		// update ここまで
		while (currentTime < et) {
			loopCount++;
			int[] tmpOutput = new int[3];
			int[] beforeOutput = new int[3];
			int n = rnd.nextInt(1000);
			beforeOutput[0] = bestOutput[n][0];
			beforeOutput[1] = bestOutput[n][1];
			beforeOutput[2] = bestOutput[n][2];

			int x = Math.min(99, Math.max(0, beforeOutput[0] + rnd.nextInt(3) - 1));
			int y = Math.min(99, Math.max(0, beforeOutput[1] + rnd.nextInt(3) - 1));
			int h = Math.min(100, Math.max(1, beforeOutput[2] + rnd.nextInt(3) - 1));
			tmpOutput[0] = x;
			tmpOutput[1] = y;
			tmpOutput[2] = h;

			updateDiff(diff, beforeOutput, tmpOutput);
			int tmpScore = 0;
			for (int i = 0; i < row; i++) {
				for (int j = 0; j < col; j++) {
					tmpScore += Math.abs(diff[i][j]);
				}
			}
			// update ここから
			currentTime = System.currentTimeMillis();
			forceLine = (et - currentTime) / C;
			if (bestScore > tmpScore || forceLine > rnd.nextDouble()) {
			// update ここまで
				bestScore = tmpScore;
				bestOutput[n] = tmpOutput;
			} else {
				// rollback
				updateDiff(diff, tmpOutput, beforeOutput);
			}
		}
		（省略）		
	}
	（省略）
}

許容条件用にいくつか要素を増やしました。提出すると、9,997,766,553点。微増ですね。おそらく試行回数が足りません。（結果詳細）
とはいえ、焼きなまし法は山登り法から機械的にスイッチ可能なアルゴリズムのため、是非試すようにしてみて下さい。

マラソン強者の戦い方

前述の内容を脳内で済ませられたり、自明の行程としてサクサク進んで来られるそこのあたな、もしや名だたるマラソンランナーでは無いでしょうか。
筆者はそのような強者の方々に語れるようなレベルではないのですが、より高みに挑もうとする方々に少しでも役に立つものがあればと思い、保持しているものを共有したいと思います。

なお、ここから先は確定的に良くなる改善は少なくなり、アイディアがいくつかある中で、有効そうなものから試していくPDCAサイクルの側面が強くなります。

スコアの持ち方を変えてみる

今回の問題では、inputとの差がスコアとなっています。これを別の評価とすることで、より繊細な状態遷移を可能にできます。
スコアの持ち方のアイディアとして、下記のようなものが浮かびました。

• マス毎の差分の大小に応じてスコアに重みを付ける。
• 中央と端とでスコアに重みを付ける。
• 差分のあるマス同士の距離で重みを付ける。
• …etc.

試行錯誤の結果、一番上のアイディアについて、スコアの算出式を差分の二乗に変えることで点数の向上が見られました。9,997,889,498点。（結果詳細）

初めは大きく後半になるにつれ小さく変化させる

開始直後は差分が大きく、大きな変化が求められます。しかし、広範囲移るにつれ差分はどんどん小さくなり、大きな変化ではなく、小さい変化で詰めていく機会が増えてきます。
こちらは時間経過に応じて、変化対象に選ぶ山を制限するロジックを加えての結果です。9,998,129,683点。（結果詳細）
後半、変化対象を小さな山に限定されるためスコア計算も軽くなり、試行回数の増加も点数増加に寄与しました。

そして何より速さが足りない

同じロジックなら、より試行回数の多い方が勝ちます。さらに、今回試してみて私自身も驚いたのですが、少ない試行回数でいい感じの結果を導く機能よりも、その機能を排除し高速化一本絞った方が最終的に良い点数が出るものもありました。
最後の最後は速度で殴りに行きましょう。

（以降奮闘中）

現在9,998,818,896点。途中過程
（絶対、9999（フォーナイン）に乗せてやる！）

やったこと

• 主にスコア計算の高速化（試行回数約50万回）
• 主に焼きなましの温度管理等のパラメータ調整

やめたこと

• 特殊なスコア計算（二乗する等）
• 特殊な近傍遷移（1マス移動しながら高さを1つ変える）

最後に

ここまで読んで頂きありがとうございました。マラソン形式の面白さ少しでも伝われば本望です。
また、弊社では2018/03/03（土）に、同コンテストHack To The Futureの本選を開催予定です。
オンサイト会場へは予選上位者のみの招待となってしまいますが、オープンコンテストとして誰でも参加可能ですので、興味を持たれた方は是非チャレンジしてみて下さい。

以上