初めに
2023年3月5日から3月19日に開催されていたトヨタ自動車 実課題プログラミングコンテスト 2023 Springに参加し、14位になりました。
本記事では、このコンテストに対する私の解法を説明すると共に、より一般的な詰め込み問題に対する知見を整理し、また、本課題に対して更なる考察を行います。
ご参考になれば幸いです。

- トヨタ自動車 実課題プログラミングコンテスト 2023 Spring 14位解法
問題概要
以下に問題概要を記します。
- コンテナに荷物を詰め込む。その向き、配置、順序を最適化せよ。
- コンテナの形状は下図に示す通り。$W \times H \times D$ の直方体の四隅に、$B \times B \times D$ の直方体ブロックが置かれた形状をしている。
- 同一種類の荷物が複数個存在する場合がある。
- 各荷物は各軸について90度単位で回転可能であるが、一部の種類の荷物は底面を固定した回転しか許されない。
- 荷物の種類によって、その上に他の荷物を重ねて置けるかどうかが制限されている。
- 荷物は、真上から垂直に下ろすことで1つずつ積み込んでいく。 このため、荷物を配置する予定位置の上部の空間には他の既に配置した荷物が存在してはならない。
- 積み込まれた荷物は、底面の面積の6割以上が、コンテナの底、もしくは他の荷物に接している必要がある。
 (画像は問題文より)
(画像は問題文より)
また、スコア計算は、以下のペナルティによって行われます。ペナルティは低ければ低い程良いです。
(ペナルティ)=1000+\mathrm{MaxHeight}+(順番前後ペナルティ)+(収容失敗ペナルティ)
ただし、
- MaxHeightは積み込んだ荷物の上面の高さに関する最大値
- 順番前後ペナルティは荷物のindexに関する転倒数の1000倍の値
- 収容失敗ペナルティは上面の高さが $D$ を越えた荷物の体積の1000倍にほぼ比例する値
となっています。
このことから、本問はほぼ厳密に順序付けされた多目的最適化問題となっており、MaxHeight<順番前後ペナルティ<収容失敗ペナルティという順序になっています。
より詳細には、下記コンテストサイトからご覧ください。
問題の性質
まず、入力データの性質を概観します。
0から9999までのseedの入力に関する統計情報としては、以下の通りになっていました。
荷物の個数
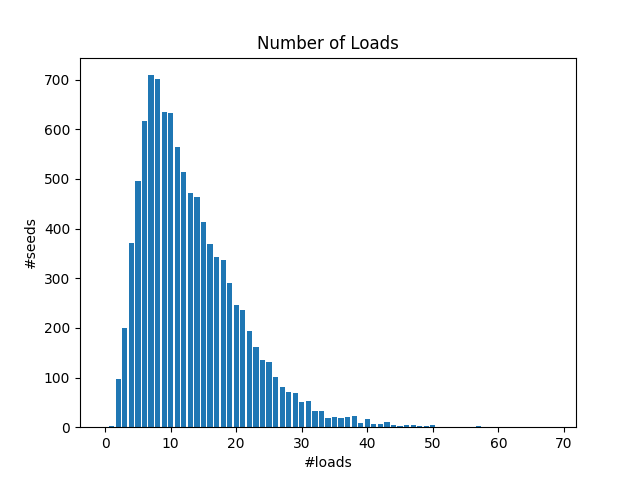
99%以上の確率で、荷物の個数は64個以下のようです。これにより、一部bit演算による高速化などが可能です。
コンテナの体積に対する荷物の総体積の割合
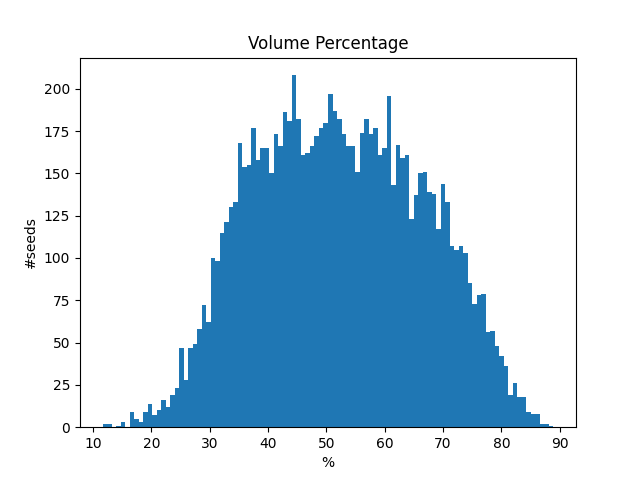
荷物の総体積の割合は、80%以下のものが大半となっています。
なお、この割合に応じて解法を少し変えることも試しましたが、私の場合、optunaによってそれは却下されました。
第1部 私の解法
それでは、私の解法を説明します。以下が最終提出です。
私の解法は以下の二要素からなります。
- 荷物の配置位置の最適化
- 荷物の詰め込み順序の最適化
この二要素それぞれについて見ていきます。
Step1 荷物の配置位置の最適化
まず、荷物の配置位置の最適化について説明します。
大まかな方針としては、ビームスタックサーチ、chokudaiサーチ、ビームサーチを足して3で割った感じ、というのが表現として最も近いと思います。
BL安定点
まず、荷物を配置する箇所の絞り込み方法について説明します。
これは他の多くの参加者の方と同じで、BL安定点をベースとして候補点を列挙しました。
BL安定点の定義は以下の通りです。
アイテムを重なりなく置ける位置の中で,左方向にも下方向にも並進させることができない位置をBL安定点という.
(出典: 株式会社NTTデータ数理システム.“BL安定点”.NTT DATA.https://www.msi.co.jp/solution/nuopt/glossary/term_adf467a563c21d8012f518718e0347411a795785.html,(最終閲覧日:2023年3月24日))
より詳細には、以下の参考文献などを参照して下さい。
梅谷 俊治.しっかり学ぶ数理最適化 モデルからアルゴリズムまで.講談社,2020.
その上で、本問には「積み込まれた荷物は、底面の面積の6割以上が、コンテナの底、もしくは他の荷物に接している必要がある」という制約があるため、単に並進不可能な点を列挙するだけでは不十分になり得ます。他の荷物の辺と合わせるようにして荷物を配置しないと、その6割を確保できない場合もあるからです。
このようなことも考慮しながら候補点を列挙しました。
関連して、四隅にある $B \times B$ のブロックも、本問特有の事情を生んでいて面白いと感じました。
通常であれば、BL点(Bottom-Left Point)、つまり、y座標→x座標の順序で最小の点を見れば事足りますが、今回はそれだけでは不都合が生じる場合があり、LB点(Left-Bottom Point)、つまり、x座標→y座標の順序で最小の点を見なければならない時もあります。

通常のBL法では面積や体積の降順で荷物を配置していくのが定石と言われていますが、今回の場合、最初から四隅に小さな $B \times B$ のブロックが存在している為、既にこの定石が破られています。なので、このような変則的なことが発生している、とも言えます。
木探索
次に、木探索の方法について述べます。
先程述べた様に、大まかな説明としては、「ビームスタックサーチ、chokudaiサーチ、ビームサーチを足して3で割った感じ」です。
それぞれの手法について、参考文献を挙げておきます。
その上で、私の解法のどのような点が各手法に由来しているかを、簡単にではありますが説明します。
ビームスタックサーチ
まず、今回の問題は、解や状態の枝刈りが極めて広範に出来る、ということが特徴として挙げられると思います。私の解法は焼き鈍し系ではなく木探索系の解法ですので、その特徴を活かすことが出来ます。
本問のペナルティは、荷物を詰め込むに従って広義単調増加しますし、また、各ペナルティの順序付けがかなり厳格なので、枝刈りが行いやすいです。
例えば、一度でも全ての荷物を収容できる解を見つけたら、それ以降は1cmでも荷物が上部からはみ出した解の探索を直ちに終了できますし、一度でも順序入れ替えなしで荷物を収容できる解を見つけたら、それ以降は1つでも順番が前後した解の探索も直ちに打ち切れます。
Shun_PIさんがコンテスト開始当初に言及されていた、枝刈り乱択という解法も大いに参考にさせて頂きました。
そして、木探索系の手法で枝刈りが重要となると、真っ先に思い出されたのがビームスタックサーチだったので、先述のtsukasaさんの記事をもう一度読み込みなおすことが出発点となりました。
ビームスタックサーチは分枝限定法にビームを導入したものである
とは、その記事で主張されていらっしゃることですが、正にそういった解釈でも理解出来ると思われます。
このような考え方に基づき、ありとあらゆる場面で徹底的に枝刈りを行うことで探索の効率化と高速化を図りました。
chokudaiサーチ
その上で、最初はほぼchokudaiサーチ的な手法を用いていました。
細いビームを何回も打つという点や、既に見た状態を一部保持するという点は、最終的な解法においても取り入れられている考え方です。
また、荷物を置く順序も、基本は体積の降順ですが、ビームごとに少しランダムな置換を加えています。
しかし、後述する工夫等の関係で、次第にビームサーチへと寄っていきました。
ビームサーチ
以上の考えを基に、ビームサーチをします。
今回行った高速化の内、特に重要な工夫として、「(遷移ごとに)状態をコピーするのではなく毎回知りたい状態をシミュレーションする」という工夫が挙げられます。
これはrhooさんの記事において言及されている手法です。実装に相違点こそありますが、根本的なアイデアは全く同じです。
具体的には、特定の荷物をおく、という操作を各ノードに見立てて、それを毎回計算することで、現在の荷物の配置状況を復元します。
それにより、解の情報をコピーする回数が大幅に減り、高速化に繋がります。

また、このような状態の持ち方をすることで、必要な安定点、不要な安定点を各ノード毎に効率的に持たせることも可能になり、安定点の計算を一部省略することも出来ました。
(プロファイリングの結果、この安定点の列挙が特に時間のかかる操作だと判明していたので、この部分の高速化の寄与はそれなりに大きいと思われます)
他にも、ハッシュによって重複除去をしたり、多様性確保の為に評価関数を複数用意したりした他、(これもrhooさんの記事で言及されていることですが)状態をシミュレーションする際に分かる、何段階か前の状態が一体どのノードに対応するのか、という情報をもとに、似たような形をした状態を減らす工夫などを行いました。
また、ビーム幅に関して、幅1のサーチをたくさん回す手法(chokudaiサーチ的手法)の方が良いのかな? とも思っていたのですが、optunaでパラメータ調整した結果、ビーム幅は43が最適という結果が出ました。
無論、一概に言える事ではないと思いますが、今回は先程示したような高速化手法の恩恵を、ある程度幅のあるビームサーチの方が受けやすいという事もあり、このような結果になっているものと思われます。
以上、荷物の配置位置の最適化について説明しました。
ところで、実はこの解法において一番大事な点を、あえてまだ説明していません。
それはビームサーチの評価関数をどのように設定するか、という点です。
これは私がコンテストにおいて最も長い時間をかけて取り組んだ点であり、最もスコアに大きな影響を与えた点でもあり、そして最も得られた成果が少ない点でした。
実は、最終的な私の解は、8割程度の確率で何の指標も使わず、ただ乱数に従った優先度でソートするだけ、という、それで本当にビームサーチと呼べるのかといったような評価関数が採用されることとなりました。
自分でもここが一番悔いの残る点ではあります。
この辺りの葛藤や試行錯誤は、後述させて頂きます。
Step2 荷物の詰め込み順序の最適化
続いて、荷物の配置を決めた後に、荷物の詰め込み順序の最適化を行うことを考えます。
(なお、予め断わっておくと、この部分のスコアに対する寄与は恐らく極めて軽微であり、コンテストでの順位を上げるという観点から言えば、かなり無駄な部分です。それは相対スコア制だということや、多目的最適化問題の重み付けの仕方などが原因です。しかし、現実問題としては、それなりに意味のある操作だとは思います)
この時点では、Step1によって荷物の配置が既に定められています。なので、この配置に適合する順序を、順番前後ペナルティが出来るだけ小さくなるように決定したい、というのが今の状況です。
ここで、「荷物を配置する予定位置の上部の空間には他の既に配置した荷物が存在してはならない」という制約は、「荷物Aは荷物Bの先に詰め込まれなければならない」という有向辺の形をした制約になるので、結局、以下の問題が解ければ良いです。
$N$ 頂点 $M$ 辺の有向グラフ $G$ が与えられる。各頂点 $i$ には、$\mathrm{kind}_i$ という種類が割り当てられている。
この時、$G$ のトポロジカル順序であるものの内、$\mathrm{kind}$ に関して転倒数最小の長さ $N$ の順列 $\mathrm{ord}$ を求めよ。
例を画像に示しました。左側にある図は荷物を詰め込んだ様子を横から見たものだとお考え下さい。この結果、今回は1,2,3,5,4という順列($\mathrm{ord}$)であれば、条件を満たし、かつ、転倒数は1と最小です。

ここで、画像にもある通り、この問題は転倒数最小の順列を求める代わりに、辞書順最小の順列を求める事でも、それなりに良い解を得ることが出来ます。実際、上の例では両者が一致しています。
基本的に $\mathrm{kind}$ の小さいものが前に来れば、転倒数は小さくなると考えられるので、辞書順最小の順列を求める事には妥当性があります。
また、$\mathrm{kind}$ が全ての頂点で相異なる場合、辞書順最小の順列を求めることは比較的容易です。
通常のトポロジカルソートを行う際に、入次数が0になっている頂点集合から、都度 $\mathrm{kind}$ が最小の頂点を選ぶようにすれば良いです。(このアルゴリズムが正当なことは、順列をnext_permutationで列挙して愚直解を計算し、それと照らし合わせる事でも確認しました。また、ABC223-Dが正にこの問題らしいです)
しかし、辞書順最小の順列は、必ずしも転倒数最小の順列になるとは限りません。

この例はiaNTUさんのTweetから例を借用させて頂き、掲載の許可を頂きました。ありがとうございます。
確かにそうですね、ケースが悪いです。
— iaNTU (@iaNTU_) March 7, 2023
このケースならどうですか?
1 → 4
1 → 5
5 → 2
5 → 3
辞書順最小にすると 1 4 5 2 3 になる(転倒数4)
ですが、1 5 2 3 4にすると転倒数3が達成できる
このTweetにある通り、辞書順最小の順列は、転倒数の最小値を必ず取る訳ではありません。なので、本問題は、あまり簡単な問題ではないだろうと考えられます。
余談ですが、辞書順最小の順列について、同一の $\mathrm{kind}$ が複数ある場合は、必ずしもこの方法で辞書順最小の解が得られるとは限らない事に注意して下さい。以下の例では、2と3が同一の種類の荷物です。

先述のアルゴリズムにおける、「$\mathrm{kind}$ が最小の頂点を選ぶ」ということが実行不可能な場合がある為、そのタイブレークを適切に処理しなければ、正確な辞書順最小の順列は得られません。
転倒数最小トポロジカルソートの解法
さて、以上の考察を基に、本問題に対する効率的な解答を与えます。
先程も触れた、iaNTUさんによるTweetのリプライにかなり大きなヒントを頂きましたが、bitDPをビームサーチによって簡略化することでも本問題は解くことが出来ます。
まず、通常のトポロジカルソートと殆ど同じ流れで行う点は変わりありません。
ここで、先程は入次数が0になった頂点集合から、$\mathrm{kind}$ が最小の頂点だけを選んでいましたが、今度はこれを全て試すことを考えます。(実際に全てを試す訳ではありませんが)
これまでにどの頂点を選択したか(64頂点以下の場合は、これは64bit整数にbit毎のflagを立てることによって管理出来ます)と、現在の入次数(トポロジカルソートをする上での途中経過に相当)という2つの情報があれば、bitDPによって先述の遷移を全て網羅することが可能で、厳密解を得ることが出来ます。
しかし、それだけでは実行時間が長くなりすぎる場合があるので、現在までに確定した転倒数が小さいものから上位k個のみを保持して遷移するようにすれば、ビームサーチで本問題を解くことが出来ます。
この辺りの話は、以下の記事に関連や背景等を含めて説明されている為、ビームサーチが何かをご存じでない方などはこちらをご覧ください。
(なお、別の見方をすれば、重複除去の為のhashとして、bitDPのbitに相当する整数を使用している、とも解釈できます)
また、高速に事前計算することが出来る、(擬似的な)辞書順最小の解の結果によって状態を枝刈りすることも行っています。
個人的にはヒューリスティックの非常に良い例題のように感じて面白かったです。
転倒数最小トポロジカルソートのコード
以下にコードを示します。一部は省略していますが、後述のコードも合わせてご覧ください。
using namespace std;
#include <bits/stdc++.h>
namespace minInvTopoSort {
template <class T>
struct fenwick_tree {
fenwick_tree() : _n(0) {}
explicit fenwick_tree(int n) : _n(n), data(n) {}
explicit fenwick_tree(vector<T>& As) : _n(As.size()), data(As) {}
// A[idx]+=x
void add(int idx, T x) {
assert(0 <= idx && idx < _n);
idx++;
while (idx <= _n) {
data[idx - 1] += x;
idx += idx & -idx;
}
}
// Σ_[l,r)
T sum(int l, int r) const {
assert(0 <= l && l <= r && r <= _n);
return _sum(r) - _sum(l);
}
// Σ_[0,r)
T sum(int r) const {
assert(0 <= r && r <= _n);
return _sum(r);
}
// A[idx] O(logN)
T get(int idx) const {
assert(0 <= idx && idx < _n);
return sum(idx, idx + 1);
}
// debug
vector<T> state() const {
vector<T> ret(_n);
for (int i = 0; i < _n; i++) ret[i] = get(i);
return ret;
}
inline T operator[](int idx) const { return get(idx); }
private:
int _n;
vector<T> data;
T _sum(int r) const {
T s = 0;
while (r > 0) s += data[r - 1], r -= r & -r;
return s;
}
};
long long inversionNumber(const vector<int>& As, int M) {
long long ret = 0;
fenwick_tree<int> f(M);
for (size_t j = 0; j < As.size(); j++) {
ret += j - f.sum(As[j] + 1);
f.add(As[j], 1);
}
return ret;
}
struct TopoState {
vector<int> indeg, zeros, ord;
int score;
long long hash;
TopoState() : score(-1), hash(-1) {}
TopoState(const vector<int>& indeg, const vector<int>& zeros)
: indeg(indeg), zeros(zeros), score(0), hash(0) {}
TopoState(const vector<int>& indeg, const vector<int>& zeros,
const vector<int>& ord, int score, long long hash)
: indeg(indeg), zeros(zeros), ord(ord), score(score), hash(hash) {}
TopoState makeNewState(const vector<vector<int>>& adj, const vector<int>& kinds,
int p, int pruningScore) const {
int newScore = score;
for (auto& other : kinds)
if (kinds[p] > other) newScore++;
for (auto& prev : ord)
if (kinds[prev] < kinds[p]) newScore--;
if (newScore >= pruningScore) return TopoState();
vector<int> newIndeg = indeg, newZeros = zeros, newOrd = ord;
auto iter = find(newZeros.begin(), newZeros.end(), p);
assert(iter != newZeros.end());
newZeros.erase(iter);
newOrd.emplace_back(p);
for (int to : adj[p])
if (--newIndeg[to] == 0) newZeros.push_back(to);
return TopoState(newIndeg, newZeros, newOrd, newScore,
hash ^ (1ll << (p % 63)));
}
bool operator<(const TopoState& rhs) const { return score < rhs.score; }
bool operator>(const TopoState& rhs) const { return rhs < (*this); }
};
pair<int, vector<int>> topoSort(const vector<vector<int>>& adj,
const vector<int>& kinds, const int M,
const size_t TOPO_BEAM_WIDTH) {
size_t N = adj.size();
vector<int> indeg(N), zeros, ord;
for (size_t i = 0; i < N; i++)
for (int to : adj[i]) ++indeg[to];
for (size_t i = 0; i < N; i++)
if (indeg[i] == 0) zeros.push_back(i);
vector<TopoState> nowBeam;
nowBeam.push_back(TopoState(indeg, zeros));
// (大まかに)辞書順最小
while (!zeros.empty()) {
auto iter = min_element(zeros.begin(), zeros.end(),
[&](int a, int b) { return kinds[a] < kinds[b]; });
int p = *iter;
zeros.erase(iter);
ord.emplace_back(p);
for (int to : adj[p])
if (--indeg[to] == 0) zeros.push_back(to);
}
assert(ord.size() == N);
vector<int> Xs(N);
for (size_t i = 0; i < N; i++) Xs[i] = kinds[ord[i]];
int pruningScore = inversionNumber(Xs, M);
if (pruningScore == 0 || TOPO_BEAM_WIDTH == 0) return {pruningScore, ord};
vector<int> bestOrd = ord;
using TopoPQ = priority_queue<TopoState, vector<TopoState>, greater<TopoState>>;
while (!nowBeam.empty() && !nowBeam[0].zeros.empty()) {
TopoPQ nextBeam;
for (const auto& state : nowBeam) {
for (int p : state.zeros) {
TopoState newState = state.makeNewState(adj, kinds, p, pruningScore);
if (newState.score != -1) nextBeam.push(newState);
}
}
vector<TopoState> newNowBeam;
unordered_set<long long> seen;
while (!nextBeam.empty() && newNowBeam.size() < TOPO_BEAM_WIDTH) {
if (seen.find(nextBeam.top().hash) == seen.end()) {
seen.insert(nextBeam.top().hash);
newNowBeam.push_back(nextBeam.top());
}
nextBeam.pop();
}
swap(nowBeam, newNowBeam);
}
int bestScore = pruningScore;
for (auto& state : nowBeam)
if (bestScore > state.score) {
bestScore = state.score;
swap(bestOrd, state.ord);
}
return {bestScore, bestOrd};
}
} // namespace minInvTopoSort
実験概要
解法の性能を検証するために、以下のような実験を行いました。
$3 \leq N \leq 50$ の範囲でランダムに問題を100回生成し、それをnext_permutationで厳密に解く場合と、(擬似的な)辞書順最小の順列で解く場合、そして、様々なビーム幅で解く場合で、得られた転倒数の平均値を比較します。
実験用コード
こちらも、一部は省略しています。
#include <bits/stdc++.h>
using namespace std;
// clang-format off
struct Xor128{// period 2^128 - 1
uint32_t x,y,z,w;
static constexpr uint32_t min(){return 0;}
static constexpr uint32_t max(){return UINT32_MAX;}
Xor128(uint32_t seed=0):x(123456789),y(362436069),z(521288629),w(88675123+seed){}
uint32_t operator()(){uint32_t t=x^(x<<11);x=y;y=z;z=w;return w=(w^(w>>19))^(t^(t>>8));}
uint32_t operator()(uint32_t l,uint32_t r){return((*this)()%(r-l))+l;}
uint32_t operator()(uint32_t r){return(*this)()%r;}
};
struct Rand{// https://docs.python.org/ja/3/library/random.html
Rand(){};
Rand(int seed):gen(seed){};
// シードを変更します
inline void set_seed(int seed){Xor128 _gen(seed);gen=_gen;}
// ランダムな浮動小数点数(範囲は[0.0, 1.0)) を返します
inline double random(){return(double)gen()/(double)gen.max();}
// a <= b であれば a <= N <= b 、b < a であれば b <= N <= a であるようなランダムな浮動小数点数 N を返します
inline double uniform(double a,double b){if(b<a)swap(a,b);return a+(b-a)*double(gen())/double(gen.max());}
// range(0, stop) の要素からランダムに選ばれた要素を返します
inline uint32_t randrange(uint32_t r){return gen(r);}
// range(start, stop) の要素からランダムに選ばれた要素を返します
inline uint32_t randrange(uint32_t l,uint32_t r){return gen(l,r);}
// a <= N <= b であるようなランダムな整数 N を返します randrange(a, b + 1) のエイリアスです
inline uint32_t randint(uint32_t l,uint32_t r){return gen(l,r+1);}
// シーケンス x をインプレースにシャッフルします
template<class T>void shuffle(vector<T>&x){for(int i=x.size(),j;i>1;){j=gen(i);swap(x[j],x[--i]);}}
// 空でないシーケンス seq からランダムに要素を返します
template<class T>T choice(const vector<T>&seq){assert(!seq.empty());return seq[gen(seq.size())];}
// 相対的な重みに基づいて要素が選ばれます (※複数回呼ぶ場合は処理を変えた方が良い)
template<class T,class U>T choice(const vector<T>&seq,const vector<U>&weights){assert(seq.size()==weights.size());vector<U>acc(weights.size());acc[0]=weights[0];for(int i=1;i<int(weights.size());i++)acc[i]=acc[i-1]+weights[i];return seq[lower_bound(acc.begin(),acc.end(),random()*acc.back())-acc.begin()];}
// 母集団のシーケンスまたは集合から選ばれた長さ k の一意な要素からなるリストを返します 重複無しのランダムサンプリングに用いられます
template<class T>vector<T>sample(const vector<T>&p,int k){int j,i=0,n=p.size();assert(0<=k&&k<=n);vector<T>ret(k);unordered_set<int>s;for(;i<k;i++){do{j=gen(n);}while(s.find(j)!=s.end());s.insert(j);ret[i]=p[j];}return ret;}
// 正規分布です mu は平均で sigma は標準偏差です
double normalvariate(double mu=0.0,double sigma=1.0){double u2,z,NV=4*exp(-0.5)/sqrt(2.0);while(true){u2=1.0-random();z=NV*(random()-0.5)/u2;if(z*z/4.0<=-log(u2))break;}return mu+z*sigma;}
private: Xor128 gen;
}myrand;
// clang-format on
/// @ref https://ei1333.github.io/library/graph/others/topological-sort.hpp
/// @ref https://www.slideshare.net/hcpc_hokudai/topological-sort-69581002
/// @brief DAGの各ノードを順序付けし、どのノードもその出力辺先のノードより
/// 前に来るように並べる O(|V|+|E|)
/// @return {トポロジカル順序,入次数0のノード}
/// 閉路検出(閉路がある→トポソ不可能) bool is_DAG = ((int)ord.size() == N);
pair<vector<int>, vector<int>> topologicalSort(const vector<vector<int>>& adj) {
const int node_num = (int)adj.size();
vector<int> indeg(node_num);
for (int i = 0; i < node_num; i++)
for (int to : adj[i]) ++indeg[to];
vector<int> start_nodes, topological_ord;
for (int i = 0; i < node_num; i++)
if (indeg[i] == 0) start_nodes.push_back(i);
vector<int> start_nodes_for_ret = start_nodes;
while (!start_nodes.empty()) {
int p = start_nodes.back();
start_nodes.pop_back();
topological_ord.emplace_back(p);
for (int to : adj[p])
if (--indeg[to] == 0) start_nodes.push_back(to);
}
return {topological_ord, start_nodes_for_ret};
}
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
vector<vector<vector<int>>> scores(
6, vector<vector<int>>(50 + 1, vector<int>(100, -1)));
for (int N = 3; N <= 50; N++) {
cerr << N << endl;
for (int cnt = 0; cnt < 100;) {
int numOfEdges = myrand.randint(1, N * (N - 1) / 2);
set<pair<int, int>> edges;
while (int(edges.size()) < numOfEdges) {
int u = myrand.randrange(N);
int v = myrand.randrange(N);
if (u == v) continue;
edges.insert(minmax(u, v));
}
vector<vector<int>> adj(N);
for (auto& [u, v] : edges) {
if (myrand.random() < 0.5)
adj[u].push_back(v);
else
adj[v].push_back(u);
}
vector<int> order = topologicalSort(adj).first;
bool is_DAG = (int(order.size()) == N);
if (!is_DAG) continue;
vector<int> kind(N);
int kindNum = N * 2 / 3;
for (int i = 0; i < N; i++) {
kind[i] = myrand.randrange(kindNum);
}
cnt++;
if (N <= 10) scores[0][N][cnt] = minInvTopoSortSlow::slow(adj, kind);
scores[1][N][cnt] = minInvTopoSort::topoSort(adj, kind, kindNum, 0).first;
scores[2][N][cnt] = minInvTopoSort::topoSort(adj, kind, kindNum, 10).first;
scores[3][N][cnt] = minInvTopoSort::topoSort(adj, kind, kindNum, 50).first;
scores[4][N][cnt] = minInvTopoSort::topoSort(adj, kind, kindNum, 100).first;
scores[5][N][cnt] = minInvTopoSort::topoSort(adj, kind, kindNum, 500).first;
}
}
for (int i = 0; i < 6; i++) {
for (int j = 0; j <= 50; j++) {
long long sum = accumulate(scores[i][j].begin(), scores[i][j].end(), 0ll);
double avg = sum / 100.0;
cout << fixed << setprecision(10) << avg << " ";
}
cout << endl;
}
return 0;
}
実験結果
実験結果は以下の通りです。
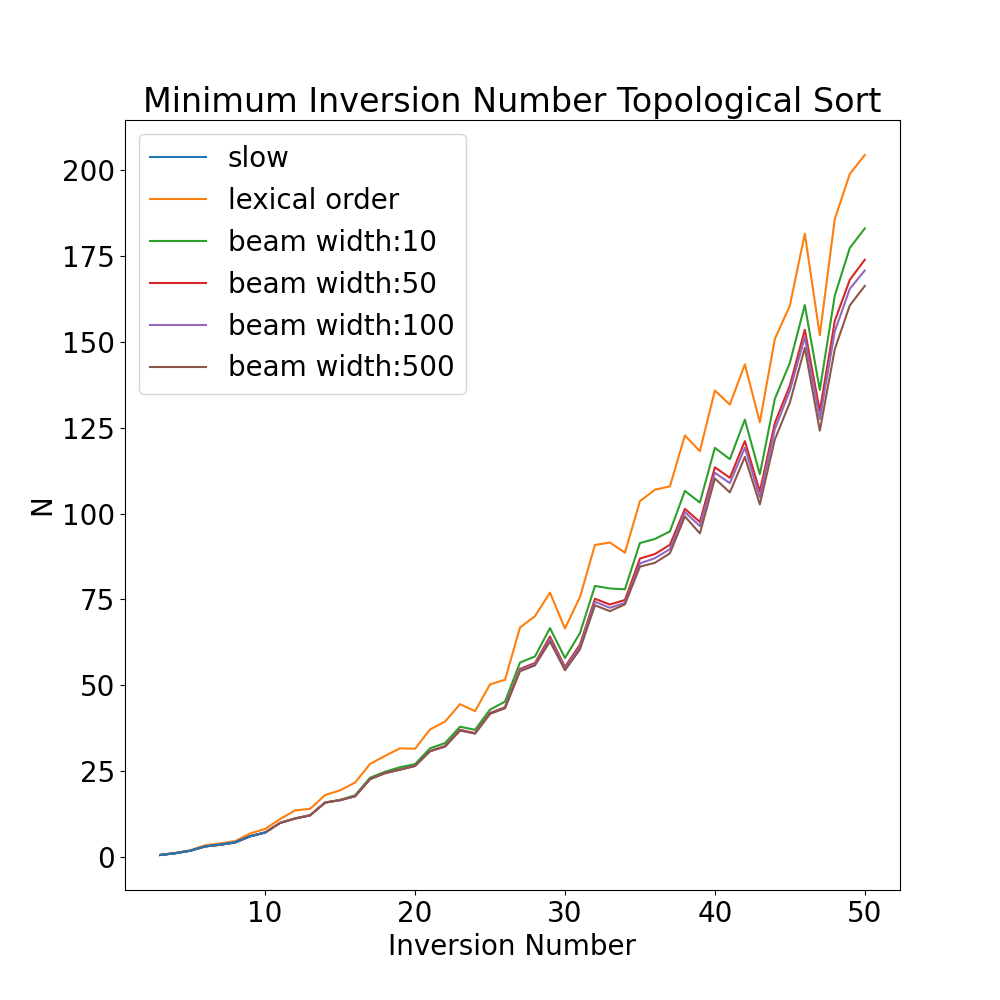
少し見づらいですが、$N \leq 10$ までは厳密解を計算しています。
そして、高々ビーム幅が10程度でも、その厳密解と全く同様の数値が得られている、つまり、極めて高い確率で厳密解を出せている、ということが窺えます。また、これは単にトポロジカルソートをするだけでは達成することの出来ない値となっています。
また、$N$ が大きい場合においても、(擬似的な)辞書順最小の解と比べて良い値を示しており、更に、ビーム幅の増加による転倒数の減少幅が頭打ちになっていることから、細いビーム幅であってもそれなりに良い解が得られていることが推察されます。
以上の結果を基に、ビーム幅20程度の探索を、Step1で得られた解に対して行うことで、順番前後ペナルティの最小化を目指しました。
追記 (2023年3月29日)
先程も言及させて頂いたiaNTUさんによると、以下のような方法でも順序の最適化がそれなりの精度で出来るようです。
(リプにある比較結果によると、「悪くても1.2倍」だそうです)
トヨタコンの順序最適化:
— iaNTU (@iaNTU_) March 26, 2023
荷物 i の上に荷物 j があると i → j の辺を張る
辺を辿って到達不可能かつ番号が小さい点の数をペナルティとし、
貪欲で取れる点の中にペナルティ最小の点を取る
計算量O(N^2)
最適ではないがいい解は出していると思う(比較してない)
これを先程のビームサーチと組み合わせると、よりより結果が高速に得られるかも知れません。
(追記終わり)
解法まとめ
以上、荷物の配置位置の最適化、荷物の詰め込み順序の最適化という2つのStepについて説明しました。私の最終的な解法は、これらを組み合せたものになっています。
また、ここにはあまり記していませんが、プロファイラによって実行時間のボトルネックになっている部分を高速化したり、optunaによって細かなパラメータ調整をしたりすることが、それなりに順位とスコアの向上に寄与しました。
ただ、逆に言えば、そのくらいしかスコアの向上に寄与しませんでした。
本当はもっと根本的な部分を改善すべきだったと反省しています。
それをするだけの時間と実装力が足りませんでした……
結果
プレテスト:43,696,806,863 (14位)
システムテスト:2,378,362,286,690 (14位)
共に14位でした。
考察
この14位という結果は、私にとっては上出来でしたが、それでも上位陣の方々とはかなり大きな差が存在します。
特に、私は優勝されたbowwowforeachさんのMCTS(モンテカルロ木探索)解に非常に納得させられてしまいました。
他の方のアプローチなので、本来ここではあまり触れるべきではないのでしょうが、勝手ながら何故このMCTS解が良い結果を残したかについても、少しだけ考察してみます。
先程もちらりと触れましたが、今回の問題はビームサーチの評価関数の作成が極めて困難でした。
私は、生のスコアを使うだけでなく、充填率を使ってみたり、z軸方向の最大値、x軸方向の最大値を使ってみたり、ペナルティの係数を変更したものを使ってみたり、非常に色々試してみましたが、結局のところはほぼ乱択に負けるという結果でした。
無論、これらの指標を使用する際、多様性の確保に失敗している可能性はあります。
しかし、恐らくそれ以上に問題なのが、これらの指標はいずれも、解を作成する途中経過において、最終的なペナルティとの相関係数が低い、という問題が挙げられると思います。
一例として、私は荷物によって生じる空隙というのを評価指標に取り入れていました。
具体的には、荷物によって塞がれてしまった空間の体積の総和を計算していました。
下図がイメージ図です。1枚目の画像にある詰め込み方の空隙+αを、視点を変えて見たのが2,3,4枚目の画像になっています。一般に、詰め込み問題は、見方を変えれば切り出し問題になります。なので、この評価指標は、空間をどれだけ効率的に切り出すことが出来ているか、という意味を持ち、有効になりそうと期待出来ます。

しかし、実は残念ながらこのような評価指標はあまりよい結果を示しませんでした。それが私のやり方が悪いせいなのかどうかは、未だ厳密には分かっていません。
ただ、たとえこの評価指標によって良いと判断されたような状態であっても、残りの荷物の数や形状によっては、必ず収容に失敗するということが起こりうる為、やはりこの評価指標も実はそんなに優れていないのではないか、と今では考えています。
また、他の参加者の方には、何やら非常に巧妙そうな評価関数を使用されている方もいらっしゃいましたが、結局それらの利点はどれ程なのか、自分の中では結論付けられていません。
そうなって来ると、評価関数を必要としない手法であるMCTSは非常に理にかなった選択だなぁ、と私は感嘆していました。
尤も、1位の方の解答を完全に把握している訳ではないので、この部分が今回の差異の本質なのかどうかは分かりません。
しかし、他の方の解答も見た上で考えると、「何らかの評価関数によって、最終的なペナルティを予測しながら解を出す」という操作しかしない私の解よりも、MCTSや解の局所性を利用した焼き鈍し法や山登り法によって、「最終的な詰め込み結果が分かっている状態から、解の巻き戻しを行って、更に探索していく」という操作を行えた方が良いのではないか、ということはかなり強く推論できそうです。
ここが上位陣と私の間の、かなり決定的な差異だったのではないかと、今では考えています。
第2部 別アプローチに関する検討
これまで私の最終提出について述べてきましたが、当然ながら最終提出以外にも色々と試行錯誤はしました。
その内の大半は、書き記す価値のない些末な事ばかりですが、焼き鈍し系の解を模索した際の取り組みには、少し普遍的な発見がありました。
以下では、それらの内容について触れます。
NFP
まず、NFPというものを取り上げます。
NFPとはno-fit polygonの略語であり、多角形PとQが重なりをもつようなQの配置位置(参照点とも。ここでは、荷物の左下の角を指す)の集合をPに対するQのNFPと言います。
 (出典: 今堀慎治, 胡艶楠, 橋本英樹, 柳浦睦憲."Pythonによる図形詰込みアルゴリズム入門".オペレーションズ・リサーチ.2018年12月.,(最終閲覧日:2023年3月25日))(画像は一部私が編集しました)
(出典: 今堀慎治, 胡艶楠, 橋本英樹, 柳浦睦憲."Pythonによる図形詰込みアルゴリズム入門".オペレーションズ・リサーチ.2018年12月.,(最終閲覧日:2023年3月25日))(画像は一部私が編集しました)
上の図を見るのが一番分かりやすいと思いますが、NFPとは要するに「置けない領域」を表している為、既に配置された荷物などに対するNFPのいずれにも属さないような点は、有効な点となります。
これによって、BL点の発見を高速化することが可能です。
より詳細には、以下の参考文献などを参照して下さい。
3次元のレクトリニア図形に対するBL点
その上で、以下のような状況設定を考えます。

左側に示したような塔を予め幾つか作成しておき、それをまとめて一つの荷物と見なします。この時、これらの塔の詰め込みを考えたいです。(ただし、塔の底面は必ずz=0を満たすとします)
これも、通常のBL法と同様の手段で高速かつ容易に計算することが出来ます。
具体的には、各z毎に塔を切ったような2次元の図形を考えて、それぞれでNFPを計算します。この時、参照点が必ずしも長方形の左下に来るとは限らないことに注意して下さい。
そのようにしてNFPを計算し、それらを全て重ね合わせた後、2次元の時と全く同じ操作をすれば、3次元の場合においてもBL点を見つけることが出来ます。
普通にやるとかなり大変そうですが、このようにNFPを応用すると簡単に計算出来ました。
NFPのコード
参考の為、私が書いたコードを添付しておきます。
NFPのいずれにも属さないようなBL点の発見は、c++ではmap<int,map<int,int>>を用いると、座標圧縮とソートが勝手に出来るので、あとは2次元のimos法を走らせるだけで良いので楽でした。
NFPのコード
#include <bits/stdc++.h>
using namespace std;
constexpr int INF = 1001001001;
struct Rect {
int x, y, x2, y2;
Rect(int x, int y, int x2, int y2) : x(x), y(y), x2(x2), y2(y2) {}
int getDX() const { return x2 - x; }
int getDY() const { return y2 - y; }
bool operator==(const Rect& rhs) const {
return x == rhs.x && y == rhs.y && x2 == rhs.x2 && y2 == rhs.y2;
}
bool operator!=(const Rect& rhs) const { return !((*this) == rhs); }
friend ostream& operator<<(ostream& os, const Rect& rhs) {
return os << "[" << rhs.x << "," << rhs.x2 << "]*[" << rhs.y << "," << rhs.y2
<< "]";
}
};
/**
* @brief NFPに対応する長方形の四隅を計算し、imosの値を入れる
* @note self.x,self.yは長方形の参照点の座標が入る。参照点が左下の角の場合は共に0
*
* @param imos 2次元のimos法を実行するためのmap imos[y][x] = val
* @param self 新たに配置する方の荷物
* @param fixed 既に配置された方の荷物
*/
void NFP(map<int, map<int, int>>& imos, const Rect& self, const Rect& fixed) {
imos[fixed.y - self.y - self.getDY()]
[fixed.x - self.x - self.getDX()]++; // NFPの左下
imos[fixed.y - self.y - self.getDY()][fixed.x2 - self.x]--; // NFPの右下
imos[fixed.y2 - self.y][fixed.x - self.x - self.getDX()]--; // NFPの左上
imos[fixed.y2 - self.y][fixed.x2 - self.x]++; // NFPの右上
}
/*
また、実際には、以下のような関数を用意して、コンテナ部分のNFPの計算を簡略化しました
auto f = [](int val) {
if (abs(val - INF) <= 10000) return +INF;
if (abs(val + INF) <= 10000) return -INF;
return val;
};
*/
/**
* @brief 2次元のimos法を実行し、BL点を見つける
*
* @param imos NFPの情報が既に入ったmap
* @return pair<int, int> BL点 発見できなければ{-1,-1}
*/
pair<int, int> findBL(const map<int, map<int, int>> imos) {
map<int, int> imos1d;
for (const auto& [y, imosY] : imos) {
for (const auto& [x, diff] : imosY) {
imos1d[x] += diff;
}
if (abs(y) == INF) continue;
int cnt = 0; // 何個のNFPに被っているか
for (const auto& [x, diff] : imos1d) {
cnt += diff;
if (abs(x) != INF && cnt == 0) {
return {x, y};
}
}
assert(cnt == 0);
}
return {-1, -1};
}
別アプローチについてのまとめ
以上、NFPなどについて紹介しました。
尤も、私がやった範囲内では、先に塔を作ってから後でコンテナに詰め込む、というこの方針はあまり上手く行かず、没案になってしまいました。しかし、やっている中で非常に面白いなと感じた部分もあった為、知識等の整理をしてみました。
これが有用であれば幸いです。
第3部 本課題に対する更なる考察
さて、先程の節までで、私がコンテスト期間中に行った考察等はほぼ全て述べたのですが、もう少しだけ気になったことがあったので、以下ではそれについて記していきます。
今回のコンテストは、「実課題」とその名にある通り、TOYOTAさんが抱えていらっしゃる現実問題を定式化し、それを競プロのコンテストの形に落とし込んだものでした。
先日渋谷で行われた、トヨタ自動車株式会社様が主催のプログラミングコンテストのパネルディスカッションにおいて、その「実課題」の詳細が恐らく初めて公表され、個人的には非常に興味を引かれました。
本当はこのように、割と小さめの籠と段ボール箱からなる問題だったのですね。
 (画像はkuruton456さんのツイートより拝借させて頂きました)
(画像はkuruton456さんのツイートより拝借させて頂きました)
さて、その上で、これはよくある話ですが、この現実問題の「定式化」は果たして本当にこれで良かったのか? という疑念が、この写真を見せて頂いた時から生じています。制約不足の為に、最適化の結果として思わぬ不都合が生じてしまっていたり、逆に不要な制約が存在してしまっていたりするかも知れません。
(尤も、今回の定式化は、コンテストに出題する問題としては、非常にバランスのとれた良い問題だったのではないかと思います。制約などが複雑化すると、ゲームとしてつまらなくなるのは至極当然な事なので……)
以下ではそのような観点から2つの問題点について議論していきます。
定式化の問題点
問題点1 荷物の詰め込みやすさ
まず、1点目として、「荷物の詰め込みやすさ」という観点から眺めてみます。
私は今回の問題を最初に見た際、貨物船に積み込むような巨大鉄製コンテナに、クレーンなどで座標ぴったりに正確に荷物を積み込んでいくような場面を想像していました。
しかし実際には、恐らくではありますが、人が手を使いながら正確な座標は分からないまま配置していくような場面の方が近いのではないか、と思われます。
そうなると、例えば以下のような詰め込み方はあまり良くないはずです。
 (seed=1 色付けは荷物の種類番号による)
(seed=1 色付けは荷物の種類番号による)
最初の青い荷物に注目して下さい。この荷物の下側は壁にぴったりとついていますが、左右はどことも言えない場所にまず唐突に配置されます。
そして、その後、若葉色の小さい荷物も不自然な間隔をおいて配置されますが、その後に配置されていく若草色の荷物や黄土色の荷物などによって、なるほどこれらの荷物はそういった相対関係にあるから、その位置に配置されたのだなふむふむ、と納得できます。
しかし、果たしてこの配置は本当に「嬉しい」配置、すなわち、「詰め込みやすい」配置なのでしょうか?
今回の場合、きっかりとした座標は使えないはずなので、勘で「この辺かな?」と順に詰め込んでいくしかなさそうですが、そうなると後から「実はここに別の荷物が入り込む余白を作っておかないといけなかった」などとなって、再配置の手間が非常に多そうです。上の例は荷物が少なめですが、荷物の数が多ければ多い程、その傾向は顕著になるでしょう。
もしも、私がこの配置表に基づいて荷物を詰め込んでいく作業員だとしたら、正直、「こんなデタラメな配置、詰め込みにくくてしょうがないわ!」と叫びながら、この配置を指定してきた人間の顔を殴りたくなってきます。(まぁ、この配置は私のプログラムによる出力結果なのですが……)
つまり、たとえその通りに配置すれば綺麗に詰め込めると分かっていたとしても、詰め込む座標に対して目印のようなものがなければ、「荷物の詰め込みやすさ」が著しく損なわれ、結果としてあまり嬉しくない配置結果になってしまう、ということは、この例からも明らかであると考えます。
そして、今回の問題ではそのような「詰め込みやすさ」は評価指標にないので、提出されたプログラムの多くはこのような状態になっているはずです。
なので、(もしも私の予想が正しいのであれば)この問題点に対する対処は、コンテストの問題への解法から現場の問題への解決策へと昇華するステップにおいて、必ず考慮されなければならないと考えます。
比較的簡単な対処法としては、私の解法で言えばStep2にあたる、「詰め込み順序の最適化」を工夫すれば良いです。
以下に一例を示します。

図の見方はStep2において掲載した図と同様です。
これまでの問題では、黒色の矢印だけが制約として存在していましたが、左右の関係を基に、新たに紫色の矢印を追加すれば、正確な座標が分からずとも、他の荷物との相対関係によって、比較的分かりやすい荷物の詰め込み方になるかと思われます。
あとは、先程と同様にビームサーチなどで順序を最適化すれば良いです。
(なお、6番目の荷物は、4番目の荷物の右側の角に合うように配置出来るので、制約を追加していません。その辺りは調整可能だと思います)
他の多くの方の解も、BL安定点や下にある荷物の角に合わせるようにして配置しているはずなので、このような解決策は有効になることでしょう。
ただし、そのように制約を増やしていくと、解の自由度はかなり失われるので、この方法で果たしてどこまで転倒数が最適化されるのかは、少々疑問です。
なので、荷物の配置段階から転倒数のことも気にしないといけないかも知れません。
また、多目的最適化問題に典型的な話ですが、上位の優先度がついたペナルティを減らそうとするあまり、それより下位の優先度のペナルティがおざなりになってしまいがちです。
今回は、収容失敗ペナルティが非常に大きいことから、転倒数ペナルティはあまり重視されていない傾向にあると感じています。本来は、もう少しここの優先度が高くても良いのではないでしょうか。
そういった事情も合わせて考えると、この辺りはまだまだ改善の余地があるのではないか、と考えます。
問題点2 荷物の積み重ね制限の有効性
次に、2点目として、「荷物の積み重ね制限の有効性」という観点から眺めてみます。
私はコンテスト開始当初、積み重ね制限フラグの意味を勘違いしていました。
積み重ね制限がついている荷物というのは、恐らく下図のような取り扱い注意のケアマークがついた荷物のことだと思われ、問題の制約にも「荷物の種類によって、その上に他の荷物を重ねて置けるかどうかが制限されている」と書かれています。

ですが、よくよく問題文を読み込むと、
「荷物Aが荷物Bの上に置かれている」とは、荷物Aの底面と荷物Bの上面の共通部分が正の面積を持つことを指す。荷物Bの上部の空間に荷物Aが配置されていても、間に隙間があれば荷物Bの上に置かれているとはみなされない。
となっています。
つまり、「積み重ね制限がついている荷物の上を完全に空にする」ということは必ずしも行わなくて良いことになっています。(私は当初このように勘違いしていました)
しかし、これは(コンテストの問題としてではなく、実問題としては)かなり微妙な制約の付け方な気がしています。
私が問題を解く上では、この積み重ね制限フラグのことを、目に見えない高さ1cmの空気の層が荷物の上部についているかどうか、みたいにしか扱っていません。
ですが、実際には、例えば以下のような状況がかなり容易に発生すると思われます。

ここでは、水色の荷物には積み重ね制限がついていて、青色の荷物との1cm程度の高さの差を利用してその制限をクリアしているとします。
しかし、振動などでオレンジ色の荷物が揺れてしまうと、左側から右側へと状況が変化し、水色の荷物に大ダメージが入ってしまいます。慣性がついているだけにダメージはかなり悪質そうです。
これはあまり好ましくない状況なのではないでしょうか。
そもそも、果たしてこれが本当に問題になるのか(つまり、積み重ね制限のある荷物が、どれだけ脆弱なのか)という疑問点はありますが、これが問題になると仮定します。
この時、本問題への対処としては、先程の「積み重ね制限がついている荷物の上を完全に空にする」という制約に切り替えれば、完全とは言えずとも、ある程度は対処可能かと思われます。
尤も、非常に大きな荷物が積み重ね不可能な場合もあるので、果たして本当にこのような制約でいいのか、ということについては検討の余地がありそうです。
定式化の問題点についてのまとめ
最後にもう一つだけ触れたいのが、「積み込まれた荷物は、底面の面積の6割以上が、コンテナの底、もしくは他の荷物に接している必要がある」という制約についてです。これもちょっと危ない制約なのかなと勝手に思っていたのですが、ある程度最適化された結果で考えると、実はこれが現実に沿った制約だったと判明して面白かったです。
開始当初、以下のようなTweetを見て私はゲラゲラ笑っていました。ギャグセンスがあって面白いです。
すげー怒られる積み方#TOYOTAHC2023SPRING pic.twitter.com/uDkvEIVK4W
— ざっくり (@zach_leee) March 5, 2023
このような配置も、実は6割制約を満たしているので、本問では有効な解となります。
ただ、一見あまりにも恣意的なこの配置ですが、よくよく考えると、他の荷物の状況次第では、BL安定点だけを候補点に選んでも似たような状況が十分に起こり得ます。
それが以下の例です。

この例では7,8,9が問題となります。
「相変わらず恣意的じゃないか」と思われるかも知れません。実際、恣意的に作成しています。しかし、割と簡単にこのような例が作れてしまう、というのは少々危ない気もしました。10000ケース位あれば確実に1ケースは物理的に不可能な詰め込み方をしているはずです。
ですが、この制約は「底面の面積の6割以上」と、側面や少し下にある荷物を考慮してはいません。なので、このような状況でも倒れにくい、あるいは、倒れてもそこまで大きな問題にならないのではないかなと思いました。上の例でも、7,8,9だけで見ると倒れてしまう形になっていますが、4,5,6が支えになって、不安定ではあるものの、大きくは倒れないと思います。
そういった意味まで考えると、この6割制約は極めて適切だったのではないかなと今では思っています。
以上、定式化の問題点などを述べてきましたが、恐らく、この辺りは定式化をされた作問者様方が一番よく分かっていらっしゃるのだろうとは思います。
その上で、コンテストとして成立させる為に適宜簡略化させているのではないかと推察しています。(そうでないと、ひたすらに怠い問題になる事は明白なので……)
ところで、これはポジショントークのつもりで書く訳ではないのですが、これ以上制約が増えたり複雑化したりするのであればあるほど、木探索系の解法に軍配があがっていく気がします。
木探索系の解法が持つ利点の一つに、制約の反映させやすさというのは確実にあると私は考えます。焼き鈍し系の解法を取り入れるにしても、やはりベースは木探索系にした方が、最強実用解法を作成する上では良いのではないのでしょうか。
今後、一体どのような制約を付け加えて、あるいは取り外して、そしてどのような最適化問題へと変形させるかは、コンテストの問題を解くのと同じくらい重要で、かつ、面白いものだと思うので、本記事がその為の一助になれば、ありがたい限りです。
おまけ
以下は参加記でもsummaryでも何でもなく、完全にただのおまけです。
さて、以下は完全なおまけですが、ビジュアライゼーションについて記します。
単なる私の昔の趣味ですが、3DCGが少しだけ出来るので、Blenderというソフトを用いて解をビジュアライズしてみました。
また、記事冒頭の写真はEeveeでなく、CyclysというRender Engineを使用しているので、動画よりも少し綺麗です。
やっていることとしては、私の過去記事と殆ど同一です。
ビジュアライズ用コード
blender側で設定している項目があったり、パスが自分の環境のものになっていたりする関係で、このままでは動きません。
なので、大筋が伝わって下さればいいなと思っています。
import bpy # blender特有のモジュール
import random
from typing import List, Tuple
M, W, H, B, D, N = -1, -1, -1, -1, -1, 0
cargos: List[Tuple[float, float, float, int]] = []
def blenderDelete() -> None:
for c_collection in bpy.context.scene.collection.children:
if c_collection.name == "DONT DELETE":
continue
bpy.context.scene.collection.children.unlink(c_collection)
for item in bpy.context.scene.collection.objects:
bpy.context.scene.collection.objects.unlink(item)
for _ in range(3):
bpy.ops.outliner.orphans_purge()
def addCube(p, r, x, y, z):
cargo = cargos[p]
h, w, d = cargo[:3]
dx, dy, dz = -1, -1, -1
if r == 0:
(dx, dy, dz) = (w, h, d)
if r == 1:
(dx, dy, dz) = (h, w, d)
if r == 2:
(dx, dy, dz) = (d, h, w)
if r == 3:
(dx, dy, dz) = (h, d, w)
if r == 4:
(dx, dy, dz) = (d, w, h)
if r == 5:
(dx, dy, dz) = (w, d, h)
bpy.ops.mesh.primitive_cube_add(
enter_editmode=False,
location=(x + dx / 2, y + dy / 2, z + dz / 2),
scale=(dx / 2, dy / 2, dz / 2),
)
ob = bpy.context.active_object
mat = bpy.data.materials.get(f"Material.{random.randint(1,3):03}")
ob.active_material = mat
def readInput(seed: int):
global M, W, H, B, D, N, cargos
with open(
r"\\wsl.localhost\Ubuntu\home\hari64boli64\Marathon\TOYOTA2023SPRING\in\\"
+ f"{seed:04}.txt"
) as f:
M, W, H, B, D = map(int, f.readline().split())
assert W == 1120 and H == 680 and B == 30
for _ in range(M):
h, w, d, a = map(int, f.readline().split()[:4])
N += a
cargos.append((h / 10, w / 10, d / 10, a))
def readOutput(seed: int):
with open(
r"\\wsl.localhost\Ubuntu\home\hari64boli64\Marathon\TOYOTA2023SPRING\out\\"
+ f"{seed:04}.txt"
) as f:
for _ in range(N):
p, r, x, y, z = map(int, f.readline().split())
addCube(p, r, x / 10, y / 10, z / 10)
def addAnimation():
for i in range(1, N + 1):
bpy.context.view_layer.objects.active = bpy.data.objects[f"Cube.{i:03}"]
bpy.context.view_layer.objects.active.location[2] += 500
bpy.context.view_layer.objects.active.keyframe_insert(
data_path="location", frame=10 * (i - 1)
)
bpy.context.view_layer.objects.active.location[2] -= 500
bpy.context.view_layer.objects.active.keyframe_insert(
data_path="location", frame=10 * (i - 1) + 35
)
def main():
seed = 3
blenderDelete()
readInput(seed)
readOutput(seed)
addAnimation()
if __name__ == "__main__":
main()
ちなみに、段ボールの質感を地味に凝ったのがお気に入りポイントです。
(参考文献: Ryan King Art.“Procedural Cardboard Material (Blender Tutorial)”.YouTube.2021年11月4日.https://www.youtube.com/watch?v=lHaFHPz46kM,(最終閲覧日:2023年3月23日))
また、本記事の途中で出てきた空隙の図示については、以下のBooleanモディファイアーを使用しました。非常に簡単です。
Blender最高!
最後に
以上、トヨタ自動車 実課題プログラミングコンテスト 2023 Springのsummaryでした。
個人的には反省点が多く悔しさの残るものではありましたが、同時に、得るものも非常に多かった、印象深いコンテストでした。
面白いコンテストを提供して頂いたTOYOTA様には深く感謝申し上げます。
最後までお読みいただきありがとうございました。