概要
今更ながらCADDi2019の(非公式な)ビジュアライザ、ジェネレーター、テスターを作りました。
ツールについて
まず問題を掲載しておきます。
問題文
サイズ L×L×L の立方体型の容器がある。この容器に球を詰め込むゲームを行う。
容器内の点は直交座標系によって表され、容器の頂点の座標のうち一つは
(0,0,0) であり、その頂点から最も遠い頂点の座標は (L,L,L) である。
詰め込める球は N 個あり、球 1、球 2、…、球 N と呼ばれる。球 i の半径は $R_i$ である。
これらから好きなだけ球を選び、それぞれ容器内の好きな整数座標に配置する (すなわち、球の中心がその整数座標となるように配置する)。
このとき、球が宙に浮いてもよいが、球が容器からはみ出たり球同士が重なったりしてはならない (球と容器、または球同士が接するのはよい)。
球の配置に対し、あなたの点数を以下の総和として計算する。
・ 基礎点: 球 i には基礎点 $P_i$ が定められており、球 i を容器内に設置すると $P_i$ 点を得られる。
・ ボーナス点: 近くに配置することが好ましい球のペアが M 組与えられる。よりには、4 つの整数の組 ($A_i,B_i,C_i,D_i$) が M 個与えられる。これらはそれぞれ、球 $A_i$ と球 $B_i$ を中心間のユークリッド距離が $C_i$ 以下となるように容器内に配置すると $D_i$ 点を得られることを表す。(距離が $C_i$ を超えるような配置が禁止されはしない。)
点数をできるだけ多く得られる球の配置を考えよ。最適解を求める必要はない。入力生成
各球 i のパラメータは以下のように決定される。
・ 球 i の半径 $Ri$ は、1 以上 200 以下の整数としてランダムに決定される。
・ 基礎点 $P_i$ は、1 以上 $max(1,R^3_i/100)$ 以下の整数としてランダムに決定される。
また、i 件目のボーナス点のパラメータは以下のように決定される。
・ $A_i$,$B_i$ は、1 以上 N 以下の 2 つの整数としてランダムで決定される。ただし、等しい値が選ばれた場合は再抽選を行う。その後、$A_i>B_i$ であれば $A_i$ と $B_i$ の値を入れ替える。
・ Ci は、$R_{A_i}+R_{B_i}+1$ 以上 $R_{A_i}+R_{B_i}+200$ 以下の整数としてランダムに決定される。
・ Di は、1 以上 2$R_{A_i}R_{B_i}$ 以下の整数としてランダムに決定される。
ビジュアライザについて
Blenderを使用して作成しました。(Pythonの形式をしていますが、これだけでは走りません。)
ただ、この記事にその結果が出てくるので、それを楽しんで頂けたら、というのがこの記事の趣旨です。
ビジュアライザ
import bpy # blender特有のモジュール
import sys
import random
from colormap import get_color_map # 自作関数 blender内ではpltのpathが通らない為
input = sys.stdin.readline
L, N, M = 1000, 1000, 100000
R_RATE = 1/10 # REDUCTION RATE
INITIAL_DIST = 1000
INPUT_PATH = "in.txt"
OUTPUT_PATH = "out.txt"
COLOR_MAP = get_color_map('jet')
def blender_delete() -> None:
for c_collection in bpy.context.scene.collection.children:
if c_collection.name == "DONT DELETE":
continue
bpy.context.scene.collection.children.unlink(c_collection)
for item in bpy.context.scene.collection.objects:
bpy.context.scene.collection.objects.unlink(item)
for _ in range(3):
bpy.ops.outliner.orphans_purge()
def blender_init() -> None: # 枠となる箱の設置
bpy.ops.mesh.primitive_uv_sphere_add(radius=0) # 番号調整
bpy.ops.mesh.primitive_cube_add(size=L*R_RATE, enter_editmode=False,
location=(L*R_RATE/2,
L*R_RATE/2,
L*R_RATE/2))
bpy.ops.object.modifier_add(type='WIREFRAME')
bpy.context.object.modifiers["Wireframe"].thickness = 1
mat_name = "box"
mat = bpy.data.materials.new(mat_name)
mat.use_nodes = True
bpy.data.materials[mat_name].node_tree.nodes["Principled BSDF"]\
.inputs[0].default_value = (0, 0, 0, 1)
bpy.context.active_object.data.materials.append(mat)
def get_color(level: float) -> tuple:
return COLOR_MAP[int(level*255)]
def put_sphere(i: int, radius: int, location: tuple,
point: int = None, actual_point: int = None) -> None:
if radius > 100:
seg, ring = 32, 16
else:
seg, ring = 16, 8
radius *= R_RATE
location = (location[0]*R_RATE, location[1] * R_RATE,
location[2]*R_RATE+INITIAL_DIST)
bpy.ops.mesh.primitive_uv_sphere_add(segments=seg, ring_count=ring,
radius=radius, location=location)
name = f"Sphere_{i:04}"
bpy.context.object.name = name
mat = bpy.data.materials.new(name=name)
mat.use_nodes = True
bpy.data.materials[name].node_tree.nodes["Principled BSDF"]\
.inputs[19].default_value = 0.5 # alpha
if point is None:
bpy.data.materials[name].node_tree.nodes["Principled BSDF"]\
.inputs[0].default_value = (get_color(random.random()))
else:
bpy.data.materials[name].node_tree.nodes["Principled BSDF"]\
.inputs[0].default_value = (get_color(min(1, actual_point/point)))
bpy.context.active_object.data.materials.append(mat)
bpy.context.object.active_material.blend_method = 'BLEND'
def visualize(XYZs: list, points: list, actual_points: list) -> None:
global RPs, ABCDs, orders
blender_delete()
blender_init()
print("init finished!")
unused_spheres = []
for i, xyz in enumerate(XYZs):
if i % 100 == 0:
print(i)
if xyz == (-1, -1, -1):
# put_sphere(i,RPs[i][0],(-100,50,50))
unused_spheres.append((i, xyz))
else:
if points is None:
put_sphere(i, RPs[i][0], xyz)
else:
put_sphere(i, RPs[i][0], xyz, points[i], actual_points[i])
print("put sphere finished!")
for frame, sphere_index in enumerate(orders):
if i % 100 == 0:
print(i)
try:
bpy.context.view_layer.objects.active =\
bpy.data.objects[f'Sphere_{sphere_index:04}']
bpy.context.view_layer.objects.active.keyframe_insert(
data_path="location", frame=frame)
bpy.context.view_layer.objects.active.location[2] -= 1000
bpy.context.view_layer.objects.active.keyframe_insert(
data_path="location", frame=frame+100)
except KeyError:
pass
print("animation finished!")
"""空隙を見る際に有効かと思ったが、重すぎる。
bpy.ops.mesh.primitive_cube_add(size=L*R_RATE, enter_editmode=False,
location=(L*R_RATE/2,
L*R_RATE/2,
L*R_RATE/2))
for i in range(N//100):
if i % 100 == 0:
print(i)
try:
bpy.ops.object.modifier_add(type='BOOLEAN')
bpy.context.object.modifiers["Boolean"].object =\
bpy.data.objects[f'Sphere_{i:04}']
bpy.context.object.modifiers["Boolean"].operation = 'DIFFERENCE'
bpy.ops.object.modifier_apply(modifier="Boolean")
except KeyError:
pass
print("boolean finished!")
"""
def main(color_mode=None, color_parameter=1):
global RPs, ABCDs, orders
with open(INPUT_PATH) as f:
_, _, _ = map(int, f.readline().split())
RPs = [list(map(int, f.readline().split())) for _ in range(N)]
ABCDs = [list(map(int, f.readline().split())) for _ in range(M)]
with open(OUTPUT_PATH) as f:
XYZs = [tuple(map(int, f.readline().split())) for _ in range(N)]
orders = [] # animationをする際の順位づけ用
for i, (x, y, z) in enumerate(XYZs):
orders.append(((x+y)+z*(2*L), i))
orders.sort()
orders = [order[1] for order in orders if order[0] != (-1-1)+(-1)*(2*L)]
if color_mode == 'default':
points = None
actual_points = None
elif color_mode == 'point':
points = [0]*N # 立方体に収まっている球たちに関してのみ見た時、最大何点取りうるか
actual_points = [0]*N # 実際に何点その球が稼いでいるか (共にダブルカウントしている)
for a, b, c, d in ABCDs:
a -= 1
b -= 1
if XYZs[a] == (-1, -1, -1):
continue
if XYZs[b] == (-1, -1, -1):
continue
points[a] += d
points[b] += d
# 何故かmathが壊れている 不思議すぎ
if sum((XYZs[a][i]-XYZs[b][i])**2 for i in range(3)) <= c**2:
actual_points[a] += d
actual_points[b] += d
points = [point/color_parameter for point in points]
else:
print("please set color mode ('default' or 'point')")
raise AssertionError
visualize(XYZs, points, actual_points)
if __name__ == '__main__':
main(color_mode='default')
一例として、私の提出結果をランダムに色付けするモードで表示したのがこちらです。
(なお、他の例では色に意味があるので注意して下さい)
ジェネレーター、テスターについて
言語はpythonです。不手際があれば連絡していただけると幸いです。
ジェネレーター
import os
import sys
import random
# ここは各自で変えてください
# コマンドラインからpython gen.py 100などとして実行することも可能です
NUM_OF_SEEDS = 100
# ここは変えても変えなくても
FOLDER_NAME = 'gen'
L, N, M = 1000, 1000, 100000
def main(NUM_OF_SEEDS=NUM_OF_SEEDS):
if not os.path.exists(FOLDER_NAME):
os.makedirs(FOLDER_NAME)
for seed in range(NUM_OF_SEEDS):
RPs = []
ABCDs = []
for i in range(N):
ri = random.randint(1, 200)
pi = random.randint(1, max(1, (ri**3)//100))
RPs.append((ri, pi))
for i in range(M):
while True:
ai = random.randint(1, N)
bi = random.randint(1, N)
if ai != bi:
break
if ai > bi:
ai, bi = bi, ai
ci = random.randint(RPs[ai-1][0]+RPs[bi-1][0]+1,
RPs[ai-1][0]+RPs[bi-1][0]+200)
di = random.randint(1, 2*RPs[ai-1][0]*RPs[bi-1][0])
ABCDs.append((ai, bi, ci, di))
with open(f"{FOLDER_NAME}\\{seed:04}.txt", mode='w') as f:
f.write(f"{L} {N} {M}")
f.write("\n")
for (r, p) in RPs:
f.write(f"{r} {p}")
f.write("\n")
for (a, b, c, d) in ABCDs:
f.write(f"{a} {b} {c} {d}")
f.write("\n")
print(f"\r進行状況 {(1+seed)/NUM_OF_SEEDS:.2%}", end="")
else:
print("\ndone!")
if __name__ == '__main__':
args = sys.argv
if len(args) == 1:
print(f"{NUM_OF_SEEDS}個生成します")
main()
elif len(args) == 2:
try:
print(f"{int(args[1])}個生成します")
main(int(args[1]))
except ValueError:
assert False, "引数には整数を指定してください"
else:
print(args)
print("実行方法が異なります python gen.py 100 などとしてみて下さい")
テスター
ついでに充填率とかも返します。
import sys
import math
# ここは各自で変えてください
# コマンドラインからpython judge.py "in.txt" "out.txt"などとして実行することも可能です
INPUT_PATH = 'in.txt'
OUTPUT_PATH = 'out.txt'
L, N, M = 1000, 1000, 100000
def main(INPUT_PATH=INPUT_PATH, OUTPUT_PATH=OUTPUT_PATH):
score = 0
basis = 0
bonus = 0
cnt = 0
XYZs = []
used_spheres = set()
volume = 0
try:
with open(INPUT_PATH) as f:
_, _, _ = map(int, f.readline().split())
RPs = [list(map(int, f.readline().split())) for _ in range(N)]
ABCDs = [list(map(int, f.readline().split())) for _ in range(M)]
except FileNotFoundError:
assert False, f"入力ファイルのパスが見つかりません\n指定されたパス:{INPUT_PATH}"
# チェック1 箱内か + 基礎点を加算
try:
with open(OUTPUT_PATH) as f:
for i in range(N):
x, y, z = map(int, f.readline().split())
XYZs.append((x, y, z))
r = RPs[i][0]
if (x, y, z) == (-1, -1, -1):
continue
assert 0+r <= x <= L-r, f"箱に収まっていない球が存在します(x:{x} y:{y} z:{z})"
assert 0+r <= y <= L-r, f"箱に収まっていない球が存在します(x:{x} y:{y} z:{z})"
assert 0+r <= z <= L-r, f"箱に収まっていない球が存在します(x:{x} y:{y} z:{z})"
cnt += 1
basis += RPs[i][1]
used_spheres.add(i)
volume += (4/3)*math.pi*(r**3)
except FileNotFoundError:
assert False, f"出力ファイルのパスが見つかりません\n指定されたパス:{OUTPUT_PATH}"
# チェック2 重なっていないか
for i, xyz1 in enumerate(XYZs):
for j, xyz2 in enumerate(XYZs):
if i == j:
continue
if xyz1 == (-1, -1, -1):
continue
if xyz2 == (-1, -1, -1):
continue
assert math.dist(xyz1, xyz2) >= RPs[i][0] + RPs[j][0],\
"重なり合っている球が存在します\n" \
+ f"球1:{xyz1} 半径{RPs[i][0]} 球2:{xyz2} 半径{RPs[i][1]}"
# ボーナス点を加算
for a, b, c, d in ABCDs:
if a in used_spheres and b in used_spheres:
if math.dist(XYZs[a], XYZs[b]) <= c:
bonus += d
score = basis+bonus
print("ok! this output meets the requirements!")
print(f"score: {score:,}")
print(f"(basis: {basis:,} bonus: {bonus:,})")
print(f"filling rate: {volume/L**3:%}")
print(f"number of used spheres: {cnt}/{N}")
if __name__ == '__main__':
args = sys.argv
if len(args) == 1:
print("注意 デフォルトのパスが使用されます")
main()
elif len(args) == 3:
main(args[1], args[2])
else:
print(args)
print("実行方法が異なります python judge.py \"in.txt\" \"out.txt\"としてみて下さい")
考察
以下この問題のネタバレを含みます。
要点
この問題、chokudaiさんが作成されたらしく、要点はほぼ全てこのツイートにまとまっています。
雑に見積もって、充填率100%の最高効率でも、基礎点は1ケースあたり200万に到達しない、というのが見えていれば、「ボーナス点を高めるゲーム」というのはまぁわかったかもしれません。 #CADDi2019
— chokudai(高橋 直大)🍆 (@chokudai) March 23, 2019
以下では、これを前提に書いていきます。
また、この記事を執筆するにあたり、ある二名の方の解法を非常に参考にさせて頂きました。こういった時にお名前を出していいのか分からなかったので(というか本当は一言連絡とかするべきなのかも知れませんが、二年も前なので流石に憚られました。。。)、現時点で一位の方をAさん、他もう一名、私がもの凄く賢いと感じた解法を書かれていた方をCさんと、とりあえず名前を伏せて進めていきます。リンク先がお二人の提出です。(他の方の提出も含め色々見させていただきました。)
Aさんのビジュアライズ
ではまずに、Aさんの提出結果をビジュアライズしてみます。
凄い。めちゃくちゃぎっしり詰まっていますね。
また、小さい球が多く使われていることが分かります。
球の色の意味を説明していませんでしたが、それぞれの球が獲得することの出来たボーナス点の割合をこんなかんじで色を付けています。(正確に言うとpltのjet)
赤い球ほど点が高いです。
少し考えればわかることですが、やはり真ん中に近い程暖色になりやすいです。これも考察のヒントになるかも知れません。
折角なのでwalk navigationも使ってみます。
意外に中には空隙があること、端の方に小さい球が集められている事が分かります。
まだまだ語るべき点は多いのですが、いったんこの辺で。
Cさんのビジュアライズ
では続いてCさん。(見やすさの観点からalphaなどは変えています)
随分対照的な結果ですね。
Cさんの解法の特徴を端的に表していると思う写真がこちらです。
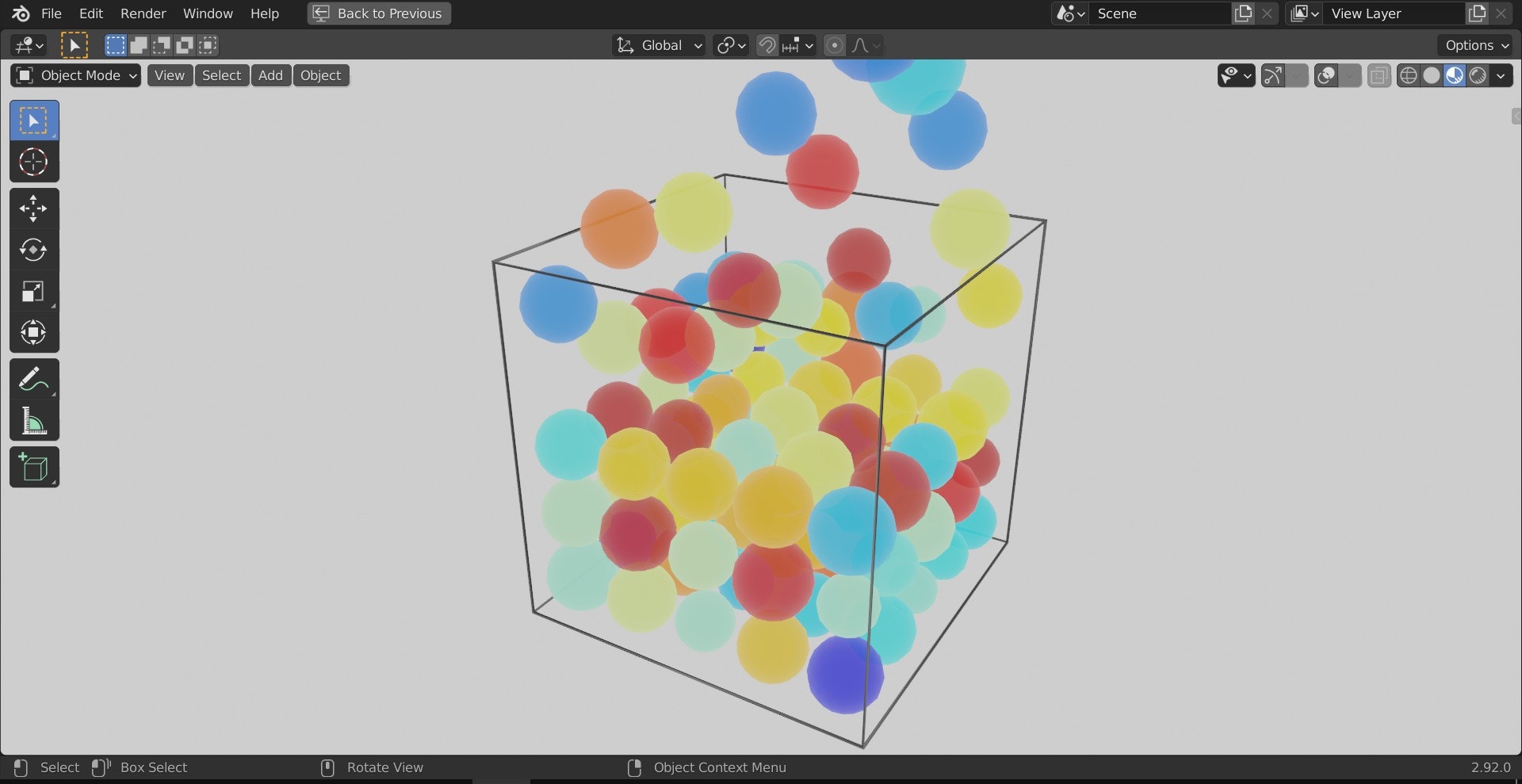
- 敷き詰め方が綺麗
- 使用している球が大きめ
- そしてとにかく赤色が多い!!!
先程のAさんの解法より球の数こそ少ないものの、真っ赤な球がいくつも確認できます。
Cさんの解法ツイートによると「方針はまず立方体で敷き詰め、各立方体には1個の球を入れて2swap焼きなまししました」「ループは190万回程度」とのことです。
焼きなましをしようにも半径の異なる球どうしを交換しては衝突してしまいそうで、近傍の取り方が難しい気がしていたのですが、なるほど、確かに立方体で最初に区間を区切ればswapも簡単そうです。これだけループを回していれば、球が赤くなる、つまりボーナス点を稼げるのも当然でしょう。
また、このツイートでも仰っている通り、色々工夫の余地がありそうなので、個人的にはとても好きな解法です。平方分割を応用発展させるようにして「立方分割」をしてみたり、あるいは分割統治法的な要領で、まず1/nサイズの立方体に球を敷き詰めて個々でスコアを最大化させた後、さらにその立方体の箱をswapさせてスコアを最大化させるなど、色々考えられます。
(さらに、Cさんの提出には思考過程もまとめられていて読んでいてとても面白かったです。)
それにしても、それぞれの解法の個性が可視化されるのは楽しいですね。
最後に
お読みいただきありがとうございました。
マラソンに興味のなかった方も、本記事を楽しんで頂けたら幸いです。